简论广义严格对角占优矩阵的判定条件

程薇薇

（齐齐哈尔工程学院 数学教研室，黑龙江 齐齐哈尔 161005）

1 主要记号

为了行文的方便和避免不必要的重复，在此给出本文常用的一些记号.

定义 1[1]设，若坌i,j∈N={1,2,…,n}，有 |aii|>Λi，坌i∈N则称 A为严格对角占优矩阵，记为A∈D，若存在正对角阵X，使AX∈D，则称A为广义严格对角占优矩阵（也称A为非奇异H矩阵），记为A∈D*

定义 2[2]设，若存在 α∈[0,1]，有 |aii|>Λiα(A)Si1-α(A)，坌i∈N，则称 A为 α-严格对角占优矩阵，记A∈Dα，若存在正对角阵X，使AX∈Dα，则称A为广义严格α-对角占优矩阵，记为A∈D*α.

2 主要结论

定理 设 A=(aij)∈Cn*n，α∈[0,1]，若坌i∈N1，

证明 （1）若 α=0，则 |aii|>Si(A)，有 AT∈D，显然 AT∈D*.

（2）若 α≠0，

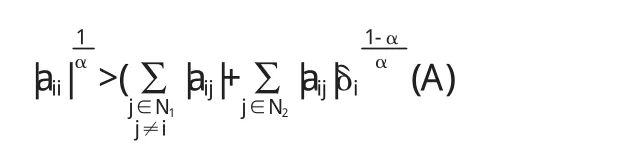
下令

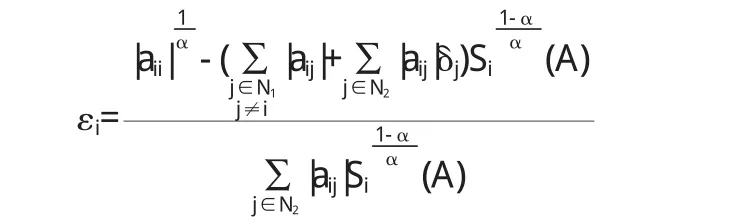
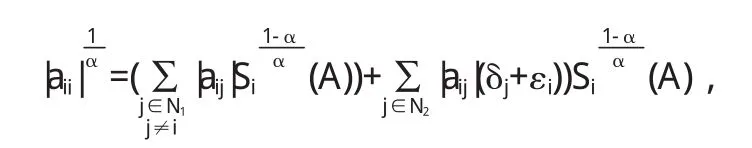
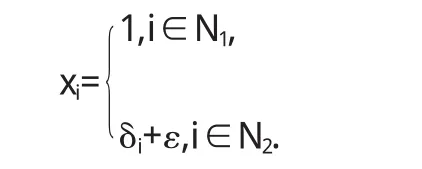
显然X1为正对角矩阵.令A1=AX1=aij(1))，则aij(1)=xjaij.

对坌i∈N1，若时，则坌i∈N2，|aij|=0.

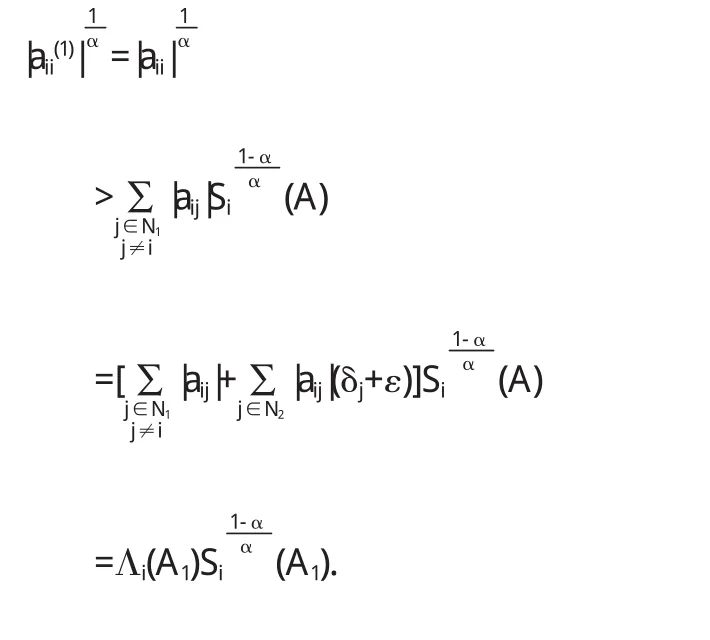
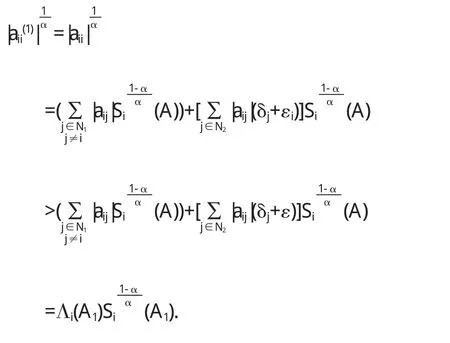
对坌i∈N2，由已知，即

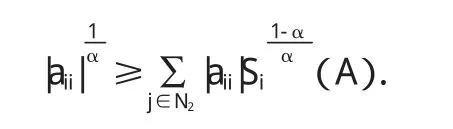
坌j∈N2,0<δj<γ<1,有

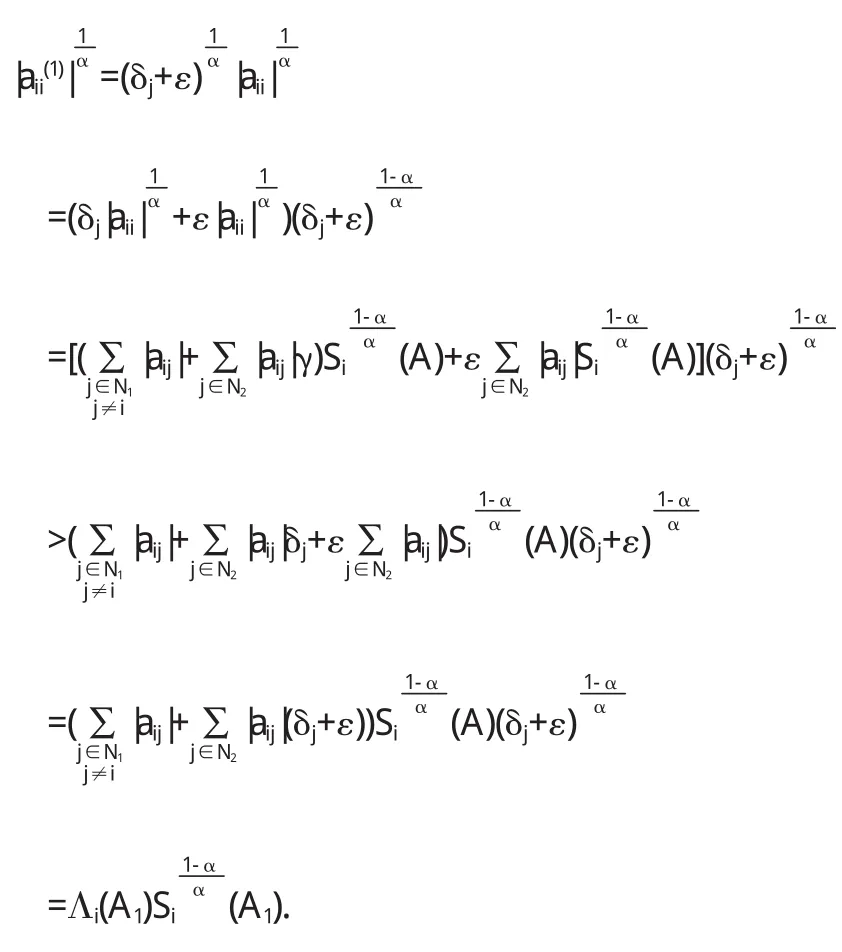
由此可见.A1=A1X=Dα，则 A∈D*α，因此知，A∈D*.

〔1〕Berman A and Plemmons RJ.Nonnegative matrices in the mathematical Sciences [M].New York:Academ ic Press,1979.

〔2〕高益明.矩阵广义对角占优和非奇异的判定[J].东北师范大学学报，1982（3）:23-28.

〔3〕孙玉祥.广义严格对角占优矩阵的充分条件[J].高等学校计算数学学报.1997(3):216-223.

〔4〕李庆春.广义严格对角占优矩阵的判定[J].高等学校计算数学学报，1999（1）:87-92.

〔5〕逄明贤.局部双对角占优矩阵及应用[J].数学学报，1995,38(4）:442-450.

〔6〕徐成贤,徐宗本.矩阵分析[M]].西安：西北工业大学出版社,1991.