一种风险型决策的效用模型及其应用
毛春华
(湖南财政经济学院,湖南 长沙 410205)
0 引言
风险型决策的最基本的决策准则是期望值准则,其基本原理是决策者应该选择行动空间中期望值最大的行动.期望值准则也是最直观处理风险决策的方法,但它不是一个很合理的准则,像著名的Petersburg悖论指出的那样,利用期望值准则可以导致不理性的决策.为解决Petersburg悖论,Bernouli在1738年提出了效用函数的概念并论述效用函数的可能形式.但是,期望效用理论在其形成与发展过程中,也遇到了一些新的挑战.最大期望效用准则在某些实际问题中显示出了偏差.如在1952年,法国数学家、诺贝尔经济奖获得者Allias就提出了著名的悖论.本文试图引进决策行动的风险,和期望效用一起作为另一个决策变量,在作出决策行动时综合考虑每一行动方案的期望效用与风险大小,该模型能很好地解释决策悖论,是对期望效用理论的完善与发展.
1 模型的建立
风险型决策问题G=(Θ,A,u),每一决策行动对于决策人来说,既具有一定的期望效用,但也面临一定的风险.所以,决策人在作出决策行动时,必须同时考虑以上两个方面的因素.因此,我们把它们作为两个决策变量,引入到同一个决策函数f[Eu,Hu]中.为此,我们首先构造一个评价决策行动优劣的决策函数f[Eu,Hu].
定义1 给出风险型决策问题G=(Θ,A,u),且行动空间中至少存在两个行动方案,如果行动方案a∈A使存在,则行动a的效用决策函数定义为
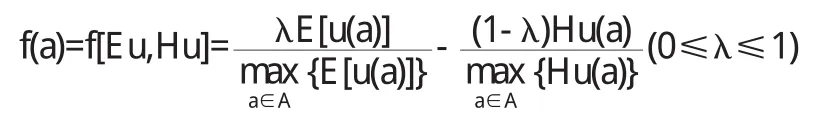
其中,E[u(a)]表示行动a的期望效用,Hu(a)表示行动a的效用风险熵,而λ表示决策者对于所面临的决策问题的期望效用和风险大小的平衡系数,它随着决策着的不同而不同,也随着决策行动空间的变化而变化.不妨称λ为决策行动的效用—风险平衡系数,一般来说,当决策者比较重视决策行动的期望效用而不重视风险大小时,λ接近于1,当λ=1时,则该决策函数就是决策行动的期望效用.反之,当决策者特别关注决策行动的风险时,λ相对较小.
显然,该效用决策函数只是一个比较性定义,它只具有相对性的含义.由决策行动空间中的各个决策行动的期望效用和每个行动本身的效用风险熵决定,它既考虑了每一决策行动对决策者所具有的主观期望效用,也考虑了每一行动所具有的不确定性大小给决策者带来的效用风险.
定义2 风险型决策问题(Θ,A,u),a1,a2∈A,如果f(a1)>f(a2),则我们称行动 a1优于 a2,即 f(a1)>f(a2)圳a1>a2.
如果存在行动a*∈A,使得,则称行动方案a*为在效用决策模型下的最优方案.
利用效用模型的决策方法可以将行动空间中的每一行动方案按其函数值的大小进行排序,从而找出其中的最优方案.
2 模型的性质
定义1风险型决策的效用模型有如下一些性质:
定理1 决策函数f[Eu,Hu]是关于期望效用E[u(a)]的增函数,是关于效用风险熵Hu(a)的减函数.且对于a1,a2∈A,如果有
E[u(a1)]≥E[u(a2)],且 Hu(a1)≤Hu(a2),则 f(a1)≥f(a2).
证明 由定义1中效用决策函数表达式

容易得出结论.
定理2 对于风险型决策问题(Θ,A,u),有
(1)若决策行动A中的所有行动方案的期望效用E[u(a)]都相同,则效用风险熵Hu(a)最小的行动是最优行动.
(2)决策行动A中的所有行动方案对应的效用风险熵Hu(a)都相同,则期望效用E[u(a)]最大的行动即为最优行动.
证明 因为每一决策行动的期望效用E[u(a)]都相同,决策函数f[Eu,Hu]是关于效用风险熵Hu(a)的减函数,从而效用风险熵最小的行动决策函数值最大,根据定义2,它是最优行动.
同理,若每一决策行动效用风险熵Hu(a)相同,决策函数是关于期望效用E[u(a)]的增函数,从而期望效用E[u(a)]最大的行动决策函数值也最大,即它是最优行动.
由以上可知,若所有决策行动的期望效用E[u(a)]相同,则只要比较它们的效用风险熵Hu(a)的大小即可,效用风险熵最小的即为最优行动;如果所有行动方案的效用风险熵Hu(a)的相同,则只要比较它们的期望效用E[u(a),期望效用最大的即为最优行动.特别地,我们有:
定理3 对于风险型决策问题(Θ,A,u),当行动空间中只有行动a1和a2时,若行动方案a1和a2的期望效用E[u(a)]相同,则效用风险熵Hu(a)小的行动即为最优行动;如果它们的效用风险熵Hu(a)相同,则期望效用E[u(a)]大的即为最优行动.
更进一步,如果两个决策行动a1和a2中,a1是确定性行动,a2为风险行动,则还有如下结论:
定理4(1)若两行动a1和a2有相同的期望效用E[u(a)],则确定性行动a1即为最优行动.(2)若两行动有相同的均值,假设决策者是风险厌恶型的,则确定性行动a1为最优行动.
证明 (1)很显然,由效用风险熵的性质可知Hu(a1)=0,Hu(a2)>0,且它们的期望效用值E[u(a)]相同,根据定理2,有f(a1)>f(a2),即a1为最优行动.
(2)设风险型行动a2的概率分布为

表1 风险行动a2的概率分布
令a1和a2的期望值为c,由于决策者为风险厌恶型的,于是其效用函数局部为上凸的,由Jesen不等式,可以得到
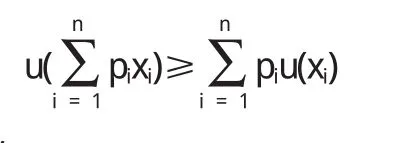
于是有

行动a1和a2的效用风险熵有Hu(x,a1)=0,Hu(x,a2)>0,因而,根据定理3有f(a1)>f(a2),即a1为最优行动.
对于如上的决策问题,如果用期望效用准则来进行决策,同样可以得出行动a1优于行动a2.即对于该决策问题,用效用决策方法与期望效用理论得到的结果相一致.由此可见,在某些情况下,两个准则得到的结论是相容的.同时,上述定理得到的结论与一个风险厌恶型的决策者凭直觉作出的决策一致.由此也可以说明,对于该决策问题,效用—风险决策模型既可以作为决策的规范化模型,也可以作为决策的描述性模型.
如果决策者为风险中性的,我们还有如下的结论:
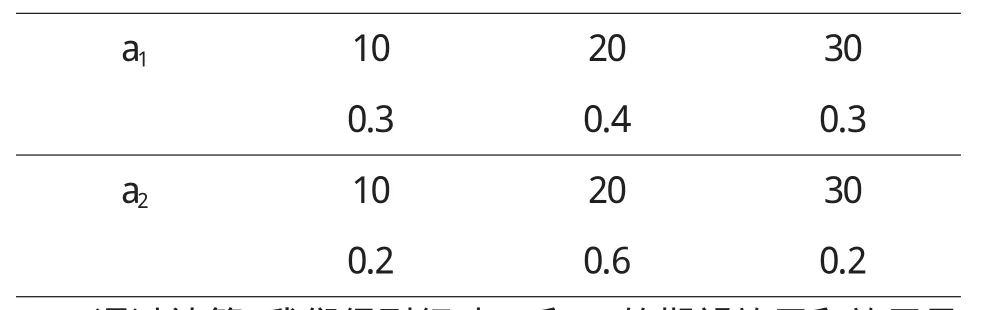
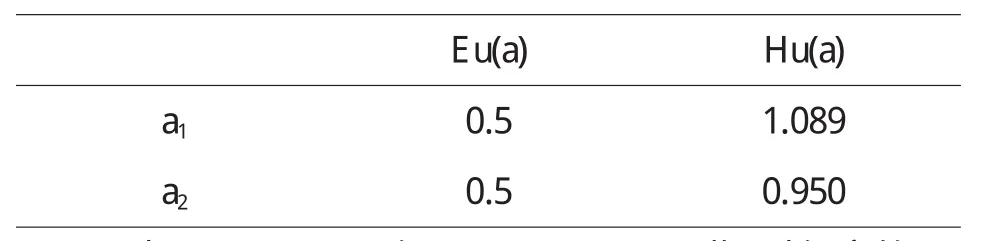
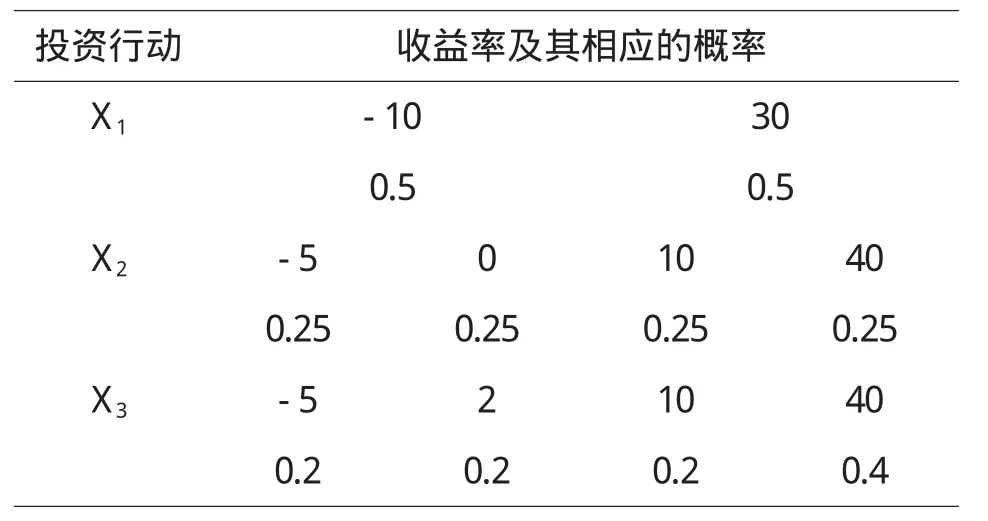
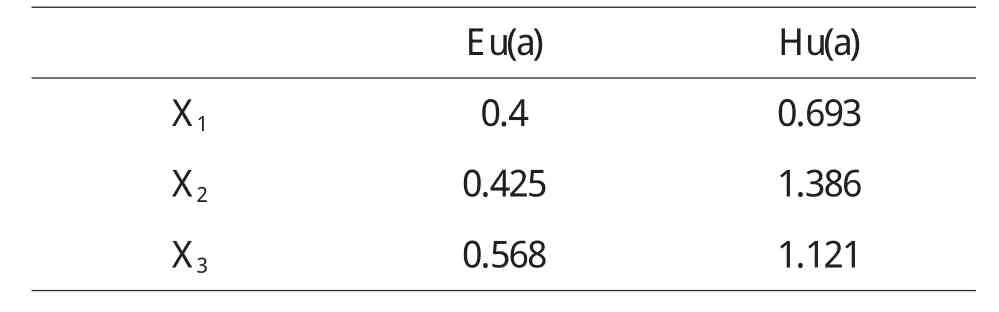
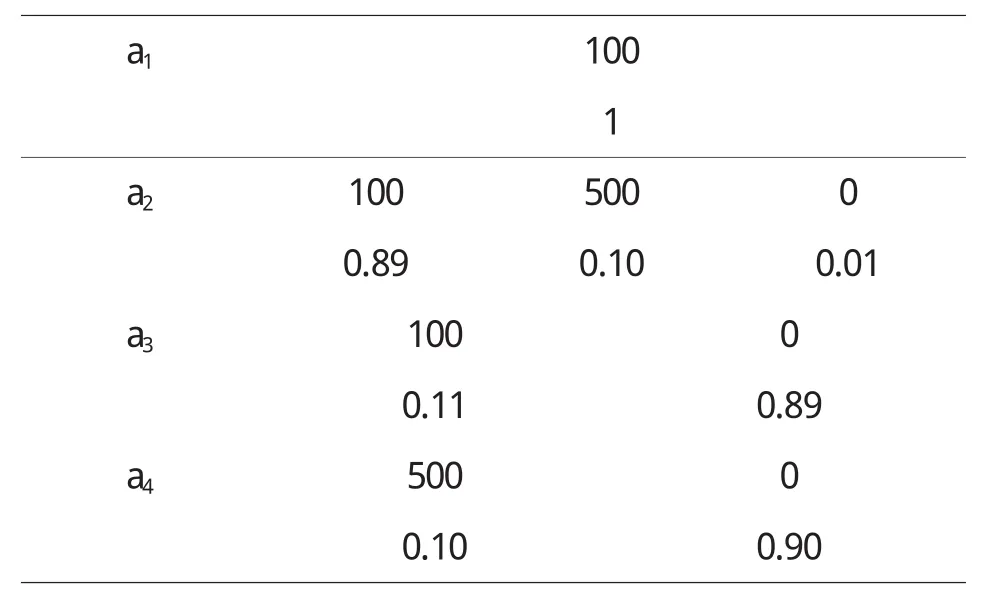
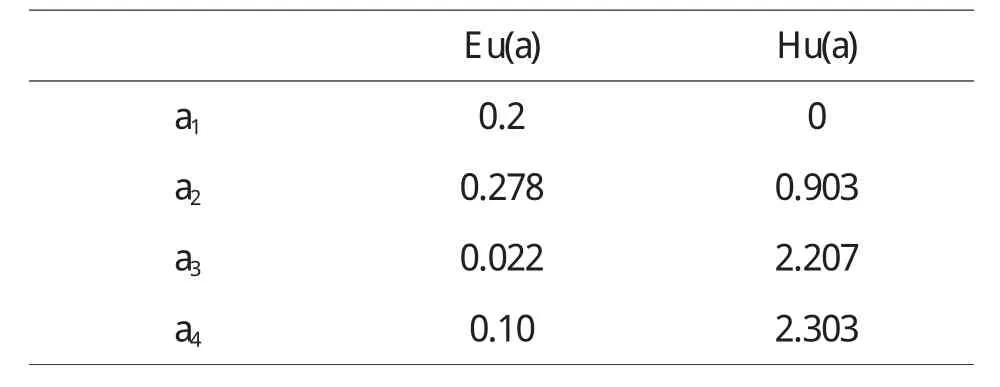
定理5 对于风险型决策问题(Θ,A,u),假定决策者是风险中性的,具有线性的效用函数,设对于行动空间中的行动a1和a2具有相同的均值,即E[u(a1)]=E[u(a2)],如果Hu(x,a1) 证明 由于决策者具有线性的效用函数,且行动a1和a2有相同的期望值,从而它们有相同的期望效用,又Hu(x,a1) 在以下实例中,假设决策者是风险中性的(其它风险情形,模型的应用方法亦相同),有线性的效用函数u(x)=,其中xmax和xmin分别表示最大的和最小的损益值.例1 设风险型决策只有两个行动a1和a2,它们分别如下 a1:以0.3的概率得到10元,以0.4的概率得到20元,以0.3的概率得到30元; a2:以0.2的概率得到10元,以0.6的概率得到20元,以0.2的概率得到30元.列表如下: 表2 风险型行动a1和a2的收益及其概率 通过计算,我们得到行动a1和a2的期望效用和效用风险熵于下表: 表3 行动a1和a2的期望效用和效用风险熵 因为 Eu(a1)=Eu(a2),但 Hu(a1)>Hu(a2),因此,对任意的 λ,由定理 3,都有 f(a1) 例2 现有三个风险型投资决策X1,X2,X3其收益率(%)及其相应的概率如下表所示 表4 风险投资行动X1,X2,X3 通过计算,我们可以得到三个行动X1,X2,X3的期望效用和效用风险熵,对其列表如下 表5 行动X1,X2,X3的期望效用和效用风险熵 很明显,由于Eu(X3)>Eu(X2),且Hu(X3) 再来分析X3与X1,假设决策者的期望效用-效用风险熵平衡系数为λ,则X3与X1的效用函数值分别 X3优于X1的充要条件为 即当且仅当0.511<λ≤1时,投资者的决策行动X3优于X1.同理,我们可以讨论X2与X1之间的优劣关系. 接下来我们进一步分析X1,X2,X3之间的随机占优关系,不难得到它们的分布函数分别为 容易验证,X1和X2之间,X1和X3之间不具有一阶随机占优关系,而对任何x,均有F3(x)≤F2(x),且至少存在一个x0,使得 F3(x0)≤F2(x0),于是 X3一阶随机占优于 X2,这与效用决策模型得到的结论一致. 例3 Allias悖论的解释,Allias决策悖论的损益值及其相应的概率可列表如下: 表6 Allias悖论的决策行动 计算它们的期望效用和效用风险熵于下表: 表7 行动a1,a2,a3,a4的期望效用和效用风险熵 于是,它们的效用决策函数值分别为 由效用决策模型,我们有 利用本文构造的决策模型比较合理的解释了Allias悖论,同时也可以看出,人的决策行为不只是考虑期望效用,其实还要考虑决策的风险因素,因此在解决风险型决策问题时,同时考虑期望效用和风险两个因素更加科学,也更符合决策者的决策行为机理. 〔1〕陈廷.决策分析[M].北京:科学出版社,1987.70~78. 〔2〕姜青舫.现代效用理论 [M].贵州:贵州人民出版社,1990.15~24. 〔3〕张尧庭,陈慧玉.效用函数及优化[M].北京:科学出版社,2000.39~42. 〔4〕Bell,D.E,One-Switch Utility Function and a Measure of risk,Managent Science,1988(34):1416~1424. 〔5〕姜丹.效用风险熵[J].中国科学技术大学学报,1993,82(2):159~168.3 模型的应用
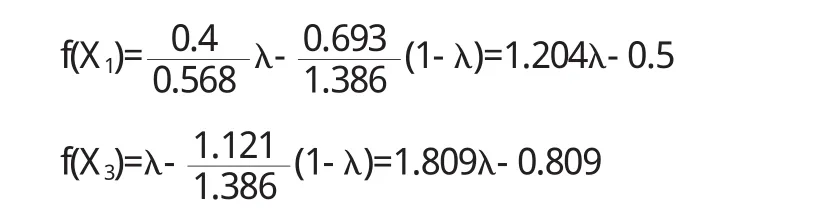
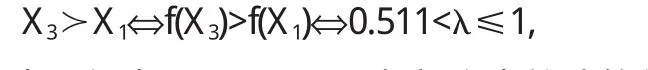
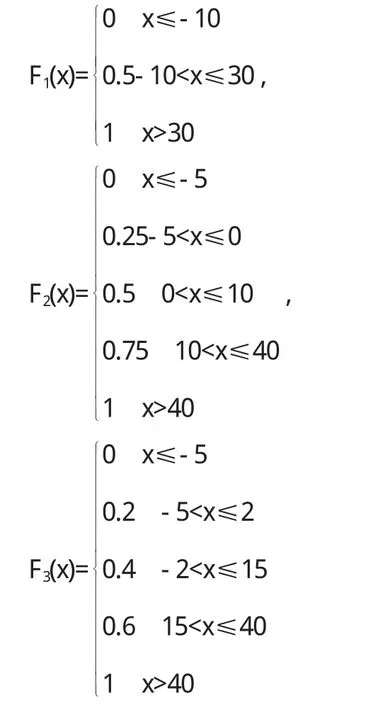

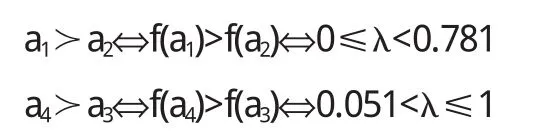
4 结束语

