介度中心和PageRank算法应用场景分析

王 敏，曹宝香，王 蕾，冯晓兵

（1．曲阜师范大学信息科学与工程学院，山东 日照276800；2．中国科学院计算技术研究所计算机体系结构国家重点实验室，北京100190）

1 概述

复杂网络中的关键点发现在实际应用中有着重要的意义。在复杂网络中总有一些节点比较重要，例如网络中的关键服务器、Web网络中用户最感兴趣的网页，以及社交网络中的意见领袖等，这些节点称为网络中的关键节点。复杂网络中的关键节点发现在实际应用中有着深远意义，例如通过保护网络中的关建服务器免受病毒或者黑客的攻击可以防止网络的瘫痪；搜索引擎可以根据用户感兴趣的网页提供一系列网页；微博中普通用户可以根据用户在某个领域的影响力关注专家，猎头公司也可以找到合适的人才等。介度中心（betweenness centrality）算法和PageRank算法是评判网络节点重要程度时广泛使用的关键点发现算法［1－2］。一般按照需求选择合适的关键点发现算法。随着社会的发展，网络呈现出多元化的发展趋势，如何在特定应用场景下选取合适的关键点发现算法成为目前要解决的重要问题，需要分析关键点发现算法的应用场景。

本文在常用的7个类型网络中选取16个真实数据集进行测试，分析2种关键点集合的差异，确定算法的应用场景。这7个网络类型分别是社交网络、通信网络、Web网络、路径网络、P2P拓扑网络、共作者网络以及蛋白质网络。首先分别计算介度中心算法和PageRank算法在这16个真实数据集上得到的关键点集合。然后统计这2种关键点集合在网络上的位置，根据它们的不同分布分析2种算法的应用场景。

2 相关工作

目前国内外的相关工作主要集中在某个特定场景下分析关键点发现算法的关系，比较有代表性的是文献［3］基于共作者网络DBLP提出的合理衡量作者贡献度的指标，文中指出PageRank值相对于其他指标，如度、介度中心等可以更合理地评价出每位作者的贡献程度。由于在DBLP网络中评价作者的贡献度时，一般根据他在本领域内的影响力，需要使用PageRank算法，因此该结论与本文分析得到的结论一致。

介度中 心［4］定 义 为 BC（v）＝ ∑s，t∈V（σst（v）／σst），即经过节点v的最短路径个数所占的比例。节点的介度中心值越高表明该节点的关键路径的条数越多，对其他节点的影响越大。PageRank算法［5］是Google公司提出的用来计算网页相对于搜索引擎中其他网页的重要程度，通过网络的超链接关系来确定一个页面的等级，将对页面的链接看成是投票，指示了网页的重要性。这2种算法定义的不同在实际应用中表现为关键点集合的不同，需要根据2种关键点集合来确定算法的应用场景。

分析这2种关键点算法的应用场景时，首先，需要确定这2种关键点集合是不一致的。然后，根据2种关键点集合的差异分析算法的应用场景。

3 2种算法应用场景的分析方法

3．1 社区分布分析

Dolphins［6］是生活在新西兰峡湾的62个海豚之间相互联系的数据集。图1是按照每个点的介度中心值画出的图（只大体画了不同家族之间的联系而且只标示排名靠前的节点的ID），节点越大表明该节点的介度中心值越大，并且将生活在同一个家族的海豚画在了一起。同样，图2是按照每个节点的PageRank值画出的海豚图。图1、图2表明，通过介度中心算法得到的关键点集合（top2）有｛13，7｝和通过PageRank算法得到的关键点集合top2有｛2，8｝是不相同的，介度中心值高的海豚13除了与本家族的海豚有联系外还与其他家族的海豚有联系，PageRank值最高的海豚2一般与本家族的海豚有联系，与外部联系相对较少。

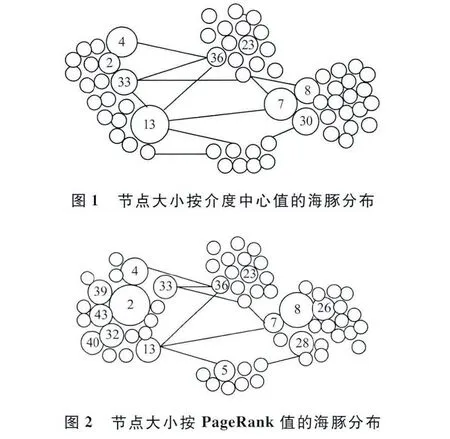
从Dolphins的实例来看，PageRank值和介度中心值的不同体现在2种关键点集合所处的网络位置上。介度中心值高的点处在社区边缘，负责整个家族的联系，对整个网络的影响较大。PageRank值较高的点一般不与其他社区联系，是社区内部被熟知的节点。这2种关键点的关系类似于某公司中部门的领导（介度中心值高）与秘书（PageRank值高）。因此，可以从在社区的分布上来分析PageRank算法和介度中心算法的应用场景。

3．2 关键点集合一致性分析

为了比较实际应用中高介度中心值的节点集合bc＿topk与高PageRank值的节点集合pagerank＿topk的差异，采用了2种评价指标，分别是topk逆序对［7］和topk集合覆盖率［7］。

为了保证制剂价格的平稳过渡及患者可接受性，公立医院在制定制剂市场调节价格过程中，大多继续坚持弥补合理生产成本支出并获得合理利润原则制定价格，主要有以下几种做法：

（1）topk逆序对

一个逆序对的定义为：｛（u，v）｜rankbc（u）＞rankpagerank（v）and rankbc（v）＜rankpagerank（u）｝，表示介度中心值排名前k个点相对于PageRank值的排名变化情况。bc＿topk的逆序对数越多表明介度中心值高的前k个点与pagerank值高的前k个点的差别越大。

（2）topk集合覆盖率

假设x为bc＿topk与pagerank＿topk相交的元素的个数，那么bc＿topk或者pagerank＿topk的集合覆盖率表示为（x／k）×100%，集合覆盖率越高表明2种关键点集合相同的节点数越高，topk集合覆盖率可以结合topk逆序对共同分析2种关键点集合的差异。

表1是介度中心值较高的前10个海豚对应的PageRank值的排名以及PageRank值高的前10个海豚所对应的介度中心值的排名。表2分别统计了dolphins网络中介度中心值高的top1，top5，top10相对于PageRank值排名逆序对和集合覆盖率情况，介度中心值最高的节点PageRank值的排名为16，是由于节点13的介度中心值排名为1，而PageRank值排名为17，变化数为16。bc＿top5的逆序对数达到了68，集合覆盖率只有20%，说明PageRank算法得到的关键点集合和介度中心算法得到的关键点集合相差较大。

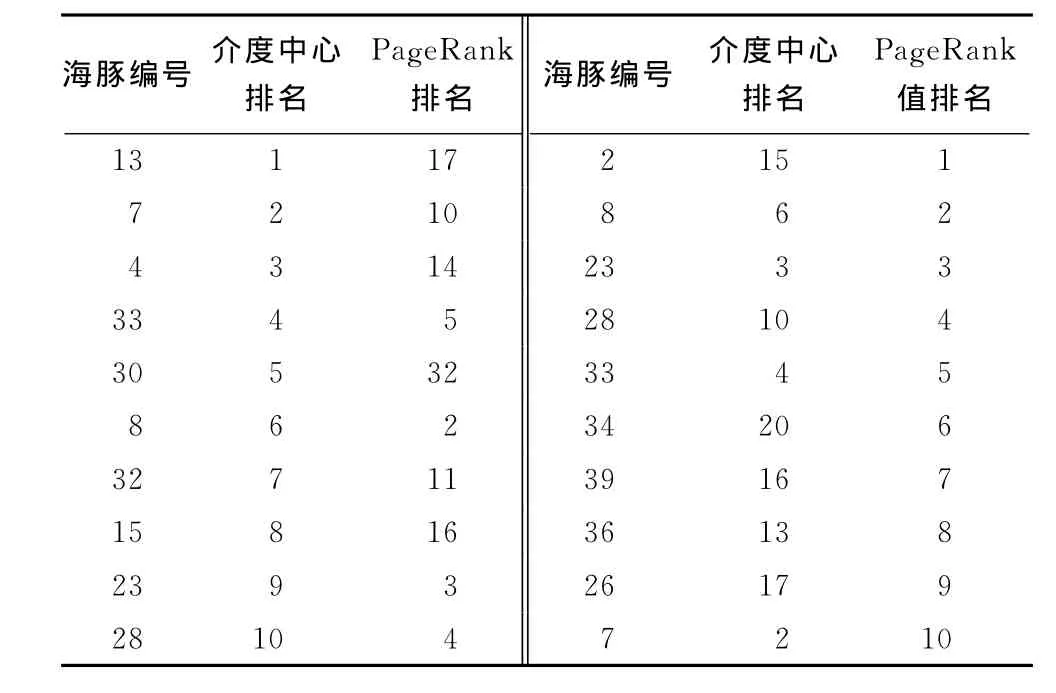
表1 介度中心值排名与PageRank值排名的对应关系

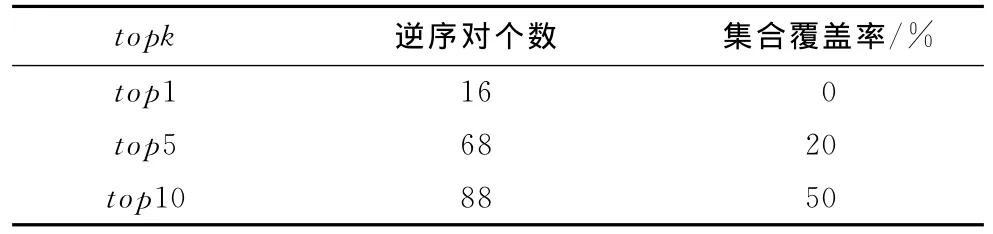
表2 topk相对于PageRank值排名的逆序对及覆盖率1

3．3 关键点集合网络位置分布差异分析

Dolphins的实例表明，PageRank值和介度中心值的差异可以体现在所在的不同网络位置上，可以根据2种关键点集合在网络中的不同位置确定其应用场景。在复杂网络分析时，常用的一个概念就是社区，可以根据2种关键点在社区分布上的不同来分析其应用场景，为了区分所在社区的不同位置，引入社区亲和度的概念，用公式描述为：

其中，Ai表示节点u连接到社区i的边数；Ei表示节点u连接到其他社区的边数；ku表示节点u的度，节点u连接的社区越多，而且与其他社区相连的边越多，cross（u）的值越小，不与其他社区相连的点的cross值为1。

P（crossv）＝（x／k）×100%

其中，x表示关键点集合中社区亲和度小于v的点数；k表示关键点集合；p（v）越大说明关键点集合的跨社区分布概率越大，集合的社区亲和度越低。

表3是Dolphins中k分别取10，20，50时bc＿topk和pagerank＿topk的社区分布（crossv＜0）情况，介度中心值高的节点跨社区分布概率要高于PageRank值高的节点，是网络中有重要影响力的点，PageRank高的节点多与社区内部的点联系，因此在寻找海豚家族的领导者时，可用介度中心算法，寻找家族的秘书时可用PageRank算法。

表3 2种关键点集合的跨社区分布概率 %

3．4 真实应用中的数据集

本文所采用的实验环境为Intel Xeon E5645的机器，Linux 2．6．32，GCC版本4．1．2，编译优化选项为－O3，单核执行。表4是测试数据集，来自于实际应用中的7个类型的网络（社会网络、通信网络、路径网、P2P网络、Web网、共作者网、蛋白质网）中的16个真实数据集。在这16个真实数据集上分析了2种算法的应用场景。

表4 测试数据集

4 实验过程与结果分析

4．1 关键点集合一致性实验

2种关键点集合是不一致的。按照不同图中高介度中心值集合相对于高PageRank值集合的覆盖率可以将测试数据集中的图分成3类，第1类覆盖率在60%以上；第2类覆盖率低于60%，高于40%；第3类测试图的覆盖率几乎为0。

表5是高介度中心值topk集合相对于PageRank值排名的变化，以及与PageRank值topk集合覆盖率的实验结果，从每个图的top100来看，逆序对数在10 000以上的图占了75%，虽然第1类图的覆盖率较高，但是逆序对数都达到了上万，顺序一致性较差，所以这2种关键点集合不是一致的。

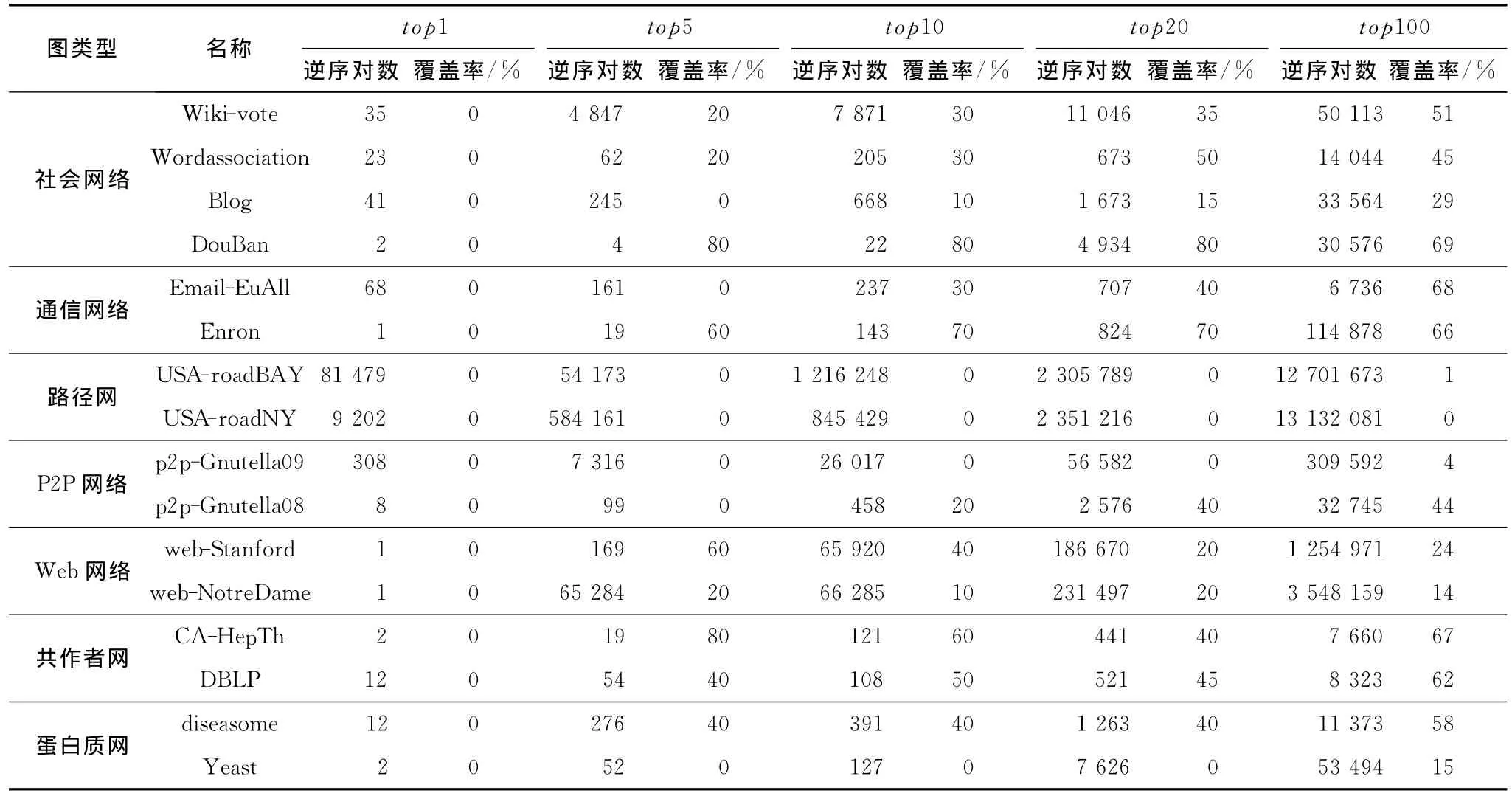
表5 topk相对于PageRank值排名的逆序对以及覆盖率2

4．2 关键点集合网络位置分布差异实验

分别统计了介度中心值高的点以及PageRank值高的点的社区分布情况（一般是社区亲和度小于0的分布），如表6所示，介度中心值高的节点社区亲和度较小，跨社区概率高于PageRank值高的点。

表6 2种关键点集合的跨社区分布概率 %

4．3 实验结果分析

不同图中高介度中心值与高PageRank值的覆盖率的分类与社区分布情况相对应。覆盖率60%以上的图中，2种关键点的社区分布情况相似，重合的点数较多；覆盖率在40%～60%的图中，介度中心值较高的点跨社区分布率多于PageRank值高的点，2种集合的覆盖率相对降低了一些；覆盖率几乎为0的测试图中，介度中心值高的节点的社区分布完全不同于PageRank值高的节点的社区分布，两者几乎没有重合的部分。

（1）覆盖率在60%以上的测试图

图3是DouBan中不同关键点跨社区分布情况，2种关键点集合在社区分布上差异较小，2种关键点跨社区分布的概率都比较大，所以两者之间会有很多相互重合的点。

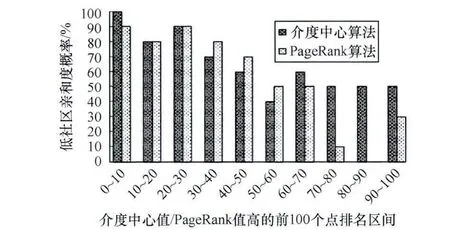
图3 DouBan网中2种关键点集合的跨社区分布概率

（2）覆盖率在40%～60%之间的测试图

图4是Wiki－Vote中不同关键点跨社区分布情况，top20覆盖率较高，2种关键点集合的分布情况相似，随着覆盖率降低，高介度中心值点跨社区概率要高于高PageRank值的点。

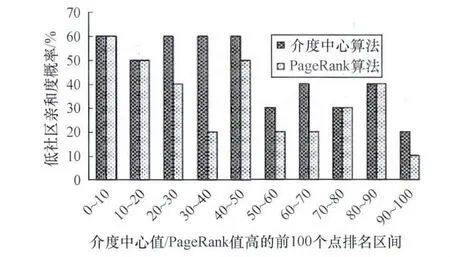
图4 Wiki－Vote网中2种关键点集合的跨社区分布概率

（3）覆盖率几乎为0的测试图

USA－roadBAY中的PageRank值高的点一般都不跨社区，而介度中心值高的点的跨社区概率要远高于PageRank值高的节点，所以2种集合相同的点数比较少，如图5所示。

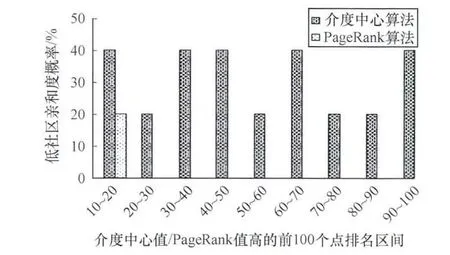
图5 路径网中2种关键点集合的跨社区分布概率

5 算法应用场景

介度中心算法的关键点分布在社区边缘，连接其他社区，对整个网络影响较大，适用于寻找整个网络重要节点的应用场景；PageRank算法的关键点分布在社区内部，是社区内活跃度较高的点，适用于寻找某领域或者部门中被广泛熟知节点的应用场景。表7总结了2种关键点集合在16个真实应用中的含义。

表7 不同关键点在测试数据中的含义

例如在DBLP中，在评价每位作者的贡献度时需要根据作者在研究领域内发表的文章数量和质量，而不是根据是否跨领域研究，在某一研究领域内有突出贡献的作者也可能在其他研究领域也有贡献，这就是在DBLP中2种关键点集合相同率较高的原因。因此，在评价作者贡献度的应用场景下就要用PageRank算法，这与文献［5］在该应用场景下得到的结论一致。

6 结束语

为了在实际应用中选择合适的关键点发现算法，本文通过分析介度中心算法和PageRank算法得到的关键点集合在网络位置上的差异，得出这2种算法各自适用的应用场景。在寻找对整个网络影响力较大的关键点时需要使用介度中心算法，在寻找某个领域内熟知度较高的关键点时需要使用PageRank算法。随着复杂网络的发展，网络的规模越来越大，算法的运行时间也较长。因此，下一步工作将从并行［21－22］和 近 似 等［23－25］角 度，研 究 如 何 降 低算法的运行时间。

［1］Page L，Brin S，Motwani R．The PageRank Citation Ranking：Bringing Order to the Web［EB／OL］．（2001－10－30）．http：／／www－diglib．stanford．edu／diglib／pub．

［2］Brandes U．A Faster Algorithm for Betweenness Centrality［J］．Journal of Mathematical Sociology，2001，25（2）：163－177．

［3］Madduri K，Ediger D，Jiang K，et al．A Faster Parallel Algorithm and Efficient Multithreaded Implementations for Evaluating Betweenness Centrality on Massive Datasets［C］／／Proceedings of IEEE International Sym－posium on Parallel and Distributed Processing．Washington D．C．，USA：IEEE Press，2009：1－8．

［4］Haveliwala T．Efficient Computation of PageRank［EB／OL］．（2001－10－30）．http：／／www－diglib．stanford．edu／diglib／pub．

［5］Liu Xiaoming，Bollen J，Nelson M L，et al．Coauthorship Networks in the Digital Library Research Community ［J］． Information Processing ＆Management，2005，41（6）：1462－1480．

［6］Lusseau D，Schneider K，Boisseau O J．Learning to Discover Social Circles in Ego Networks［C］／／Proceedings of Conference on Neural Information Processing Systems．South Lake Tahoe，USA：［s．n．］，2012：548－556．

［7］王 敏，王 蕾，冯晓兵，等．基于顶点加权的介度中心近似算法［C］／／中国高性能计算学术年会论文集．广州：［出版者不详］，2014：160－170．

［8］Nelson D L，McEvoy C L，Schreiber T．A．The University of South Florida Word Association，Rhyme，and Word Fragment Norms［EB／OL］．（1999－12－30）．http：／／www．usf．edu／FreeAssociation．

［9］Tang Lei，Liu Huan．Relational Learning via Latent Social Dimensions［C］／／Proceedings of the 15th ACM SIGKDD Conference on Knowledge Discovery and Data Mining．New York，USA：ACM Press，2009：817－826．

［10］Lei Tang，Liu Huan．Scalable Learning of Collective Behavior Based on Sparse Social Dimensions［C］／／Proceedings of the 18th ACM Conference on Information and Knowledge Management．New York，USA：ACM Press，2009：1－33．

［11］Leskovec J， Kleinberg J， Faloutsos C． Graph Evolution：Densification and Shrinking Diameters［EB／OL］．（2007－07－28）．http：／／arxiv．org／abs／physics．

［12］Klimmt B，Yang Yiming．Introducing the Enron Corpus［C］／／Proceedings of the 1st Conference on Email and Anti－Spam．Mountain View，USA：［s．n．］，2004：1－2．

［13］Delling D，Holzer M，Müller K，et al．Highperformance Multi－level Graphs［J］／／Proceedings of the 9th Discrete Mathematics and Theoretical Computer Science Implementation Challenge Workshop on Shortest Paths．Piscataway，USA：［s．n．］，2006：709－736．

［14］Bast H，Funke S，Matijevic D．Transit——Ultrafast Shortest－path Queries with Linear－time Preprocessing［C］／／Proceedings of the 9th Discrete Mathematics and Theoretical Computer Science Implementation Challenge Workshop on Shortest Paths．Piscataway，USA：［s．n．］，2006：1－17．

［15］Ripeanu M，Foster I，Iamnitchi A．Mapping the Gnutella Network：Properties of Large－scale Peer－to－Peer Systems and Implications for System Design［J］．IEEE Internet Computing Journal，2002，6（1）：1－12．

［16］Leskovec J，Lang K，Dasgupta A，et al．Community Structure in Large Networks［EB／OL］．（2008－10－08）．http：／／arxiv．org／abs／0810．1355．

［17］Albert R，Jeong H，Barabasi A L．Diameter of the World－wide Web［EB／OL］．（1999－09－10）．http：／／arxiv．org／abs／cond－mat／9907038．

［18］Yang Jaewon，Leskovec J．Defining and Evaluating Network Communities Based on Ground－truth［C］／／Proceedings of the 12th International Conference on Data Mining．Washington D．C．，USA：IEEE Press，2012：1－10．

［19］Goh K I，Cusick M E，Valle D，et al．The Human Disease Network［EB／OL］．（2007－05－22）．http：／／www．pnas．org／cgi／doi／10．1073／pnas．0701361104．

［20］Sun Shiwei，Ling Lunjiang，Zhang Nan．Topological Structure Analysis of the Protein－protein Interaction Network in Budding Yeast ［J］．Nucleic Acids Research，2003，31（9）：2443－2450．

［21］涂登彪，谭光明，孙凝晖，无锁同步的细粒度并行介度中心算法［J］．软件学报，2011，22（5）：986－995．

［22］平 宇，向 阳，张 波．基于 Mapreduce的并行PageRank算法的实现［J］．计算机工程，2014，40（9）：124－129．

［23］王钟斐，王 彪．基于锚文本相似度的PageRank改进算法［J］．计算机工程，2010，36（24）：258－260．

［24］王德广，周志刚，梁 旭．PageRank算法的分析及其改进［J］．计算机工程，2010，36（17）：291－293．

［25］姚 琳，刘 文．一种基于本体的PageRank算法的改进策略［J］．计算机工程，2009，35（6）：50－51，54．