新型Hammerstein动态非线性功放模型及其预失真应用

王振霞，南敬昌

（辽宁工程技术大学电子与信息工程学院，辽宁 葫芦岛125105）

1 概述

射频功率放大器作为通信系统的核心器件，其性能好坏将直接决定整个系统的优劣。随着无线通信系统的快速发展，更大程度的追求高效率和高线性度，对功率放大器无疑提出了更大的挑战［1］。尤其是非恒定包络、宽频带、高均峰比（如OFDM）调制方案的广泛应用，使得功率放大器出现了严重的非线性失真。因此，研究如何消除功放非线性失真，提高功放线性度具有重要的现实意义。不同于常见的线性化技术（如功率回退技术、前馈技术、包络消除与恢复技术），预失真技术可以在不降低效率的同时获得良好的线性度，这种优良的特性使其成为最有前景的线性化技术之一。预失真技术包括射频预失真、中频预失真、基带预失真［2］。其中，基带预失真技术（也叫数字预失真）因为不使用非线性射频器件，不涉及高难度的信号处理问题而倍受关注［3］。

为了更好地将数字预失真线性化技术应用于功放，首先需要为功放建立行为模型。常见的功放行为级模型，包括神经网络模型、Volterra级数模型［4］。神经网络对非线性函数的描述具有好的逼近能力，但容易陷入局部极小，泛化能力不强。Volterra级数虽然可以清晰地描述非线性系统的物理意义，但它的模型参数数量随系统的非线性和记忆长度的增加呈指数形式增长，辨识过程非常复杂。为了解决这个难题，提出利用简化的Volterra级数模型为功放建模。常见的模型有记忆多项式、包络记忆多项式、Wiener、Hammerstein、并联 Wiener、Hammerstein等模型。这些模型通过去除Volterra级数模型中的冗余项，保留对功放建模有影响的项，降低了模型复杂度［5－7］。Hammerstein模型［8］在建模精度和降低复杂度上都要优于其余模型。其建模思想是将功率放大器的非线性和记忆效应分离，然后将两者进行串联。在此模型基础上，文献［8］提出了增强的Hammerstein模型，相比传统的Hammerstein模型，建模精度有了一定的提高。但是仍然无法达到设计要求，建模精度有待进一步提高。

针对以上问题，本文在Hammerstein模型的基础上，重点考虑功放中出现的难以解决的记忆效应问题，分别构建弱记忆效应子系统和强记忆效应子系统，提出改进的Hammerstein动态非线性模型，并利用这种模型建立功放的预失真模型。

2 Hammerstein模型预失真

2．1 传统的Hammerstein模型

如图1所示，传统的Hammerstein模型是由非线性子系统（NL）级联线性因果子系统（LTI）构成的模型。

图1 Hammerstein模型结构

Hammerstein模型的数学表达式表示为：

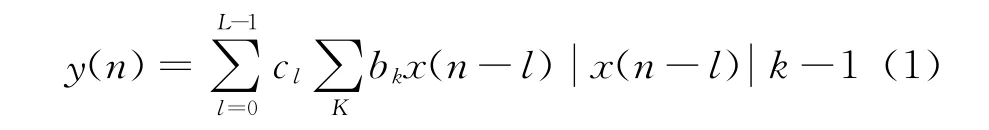
其中，cl为LTI模块的系数；bk为奇数阶NL模块的系数；K，L分别表示行为模型的非线性阶数和记忆深度。

2．2 增强的Hammerstein模型

如图2所示为增强的Hammerstein模型，模型结构通过多项式的叠加而得到的。在模型中使用了并行的FIR滤波器来表达整个模型的记忆效应。

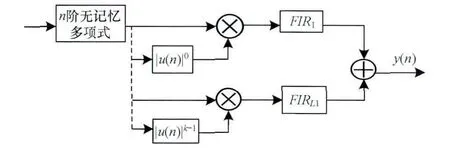
图2 增强的Hammerstein模型结构

3 功放中的记忆效应

功率放大器中记忆效应［9］的产生有多方面的原因，按照产生的位置，将记忆效应分为短期记忆效应和长期记忆效应［10］。将匹配网络引起的记忆效应称为短期记忆效应（STM），由偏置网络、自热现象引起的记忆效应称为长期记忆效应［11］（LTM）。STM的存在导致功放的输出产生带内失真，而对于LTM则主要产生的是带外失真。为了更加准确地构建出记忆效应模型，采取对短期记忆效应和长期记忆效应分别建模的方案。使用线性的FIR滤波器来补偿由于匹配网络产生的非恒定频率响应所引起的短期记忆效应［12］。使用FIR动态滤波器来补偿由于偏置网络和自热产生的长期记忆效应。

4 改进的Hammerstein模型

构建改进的Hammerstein模型的主路径，为了提高模型的精确度，增加附加路径。附加路径使用模型的输出信号与输入信号做差，目的是构建非线性模型。让所得差值分别经过弱非线性模型和强非线性模型，构建另一部分输出。如图3所示为改进的Hammerstein模型的拓扑结构。

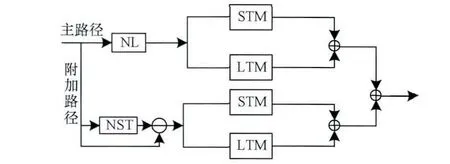
图3 改进的Hammerstein模型拓扑结构

改进的Hammerstein模型运算流程如图4所示。非线性部分采用稳定性高的查找表的方法实现，而记忆效应部分采用FIR滤波器来实现。

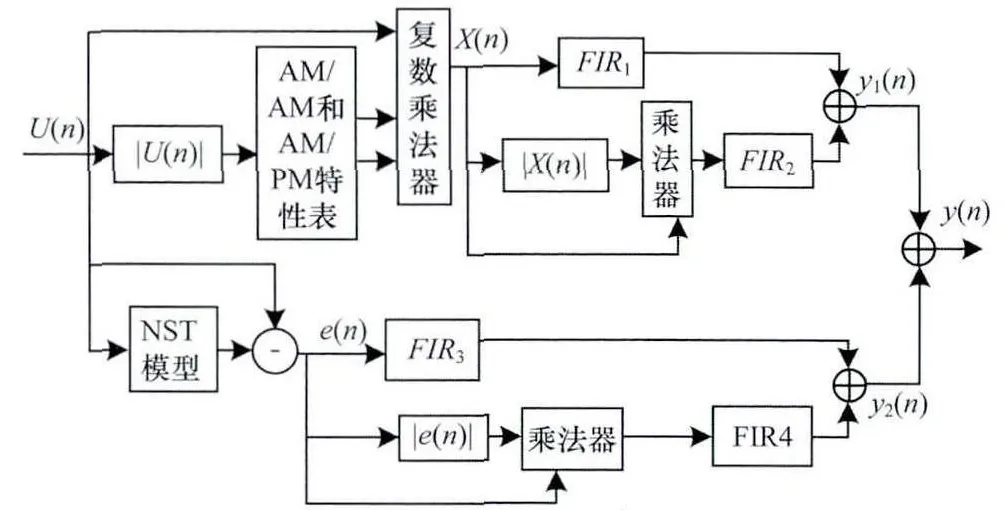
图4 改进的Hammerstein模型运算流程

改进的Hammerstein模型的数学表达式为：

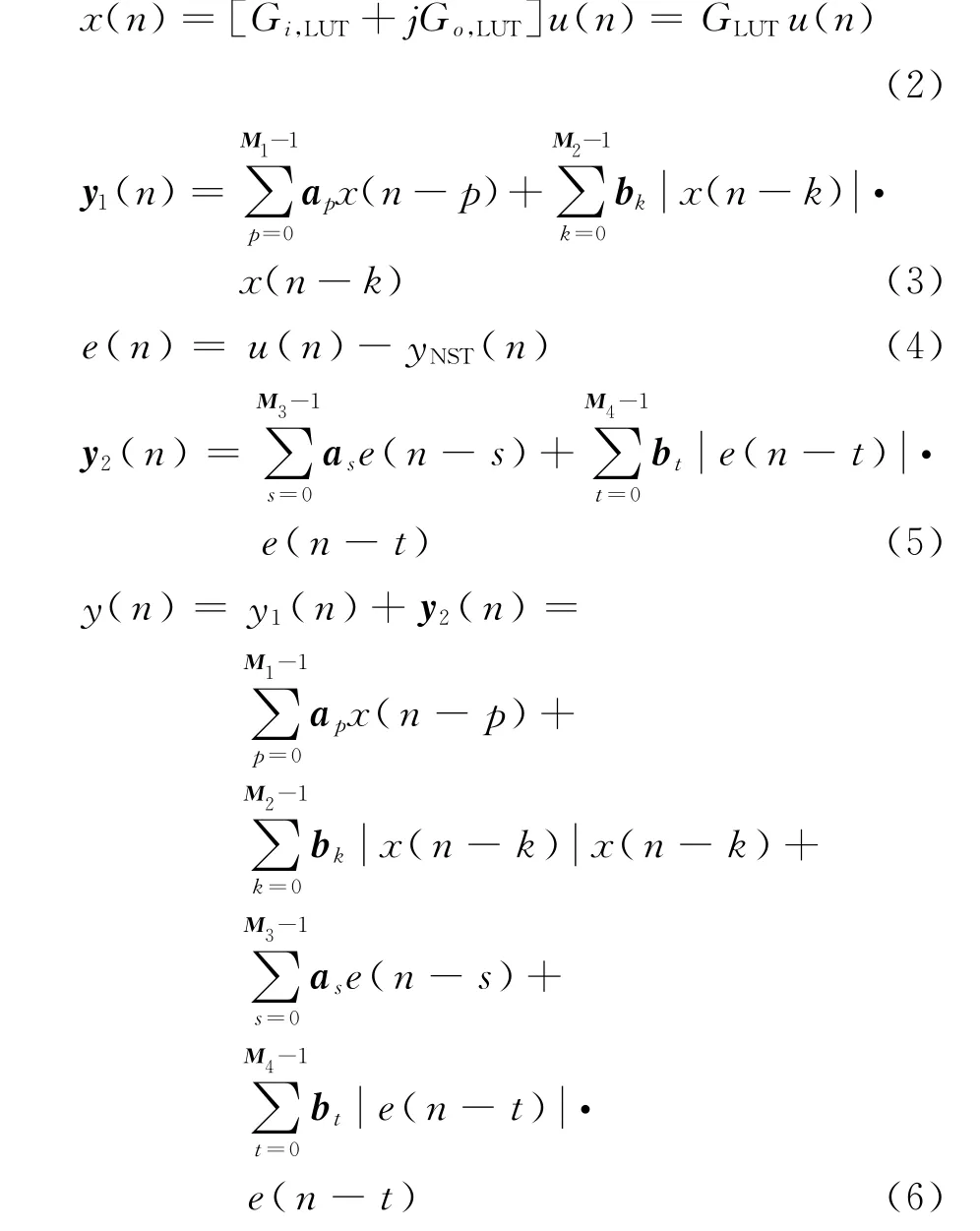
其中，GLUT表示查找表的复增益；M1和M2分别代表主路径中弱记忆效应子系统和强记忆效应子系统的记忆深度；ap和bk分别代表主路径中弱记忆效应和强记忆效应的系统参数；M3和M4分别代表附加路径中弱记忆效应子系统和强记忆效应子系统的记忆深度；as和bt则分别代表附加路径中弱记忆效应和强记忆效应的系统参数。由于查找表是基于数据分析的方法，能很好地表征模拟域不连续的模型，另外由于具有良好的稳定性，易于在基带实现。因此改进的Hammerstein模型的非线性模块通过查找表来实现。而对于功放中的记忆效应模块，则通过弱记忆效应子系统级联强记忆效应子系统实现。更加精确地表征了功放中的记忆效应，提高了模型的精度。为了进一步提高模型的精度，加入了附加路径。与传统的Hammerstein模型相比，精确度有了显著提高。

5 模型仿真与验证

选用Nitronex公司的高电子迁移率的GaN制作的NPT1004进行功放的设计，其工作频段为0～4GHz，静态工作点为 VDS＝28V，IDS＝350mA，VGS＝－1．5V，利用电磁仿真软件 ADS2009（Advanced Design System），使用负载牵引技术设计匹配电路，得到完整的电路原理图，如图5、图6所示。

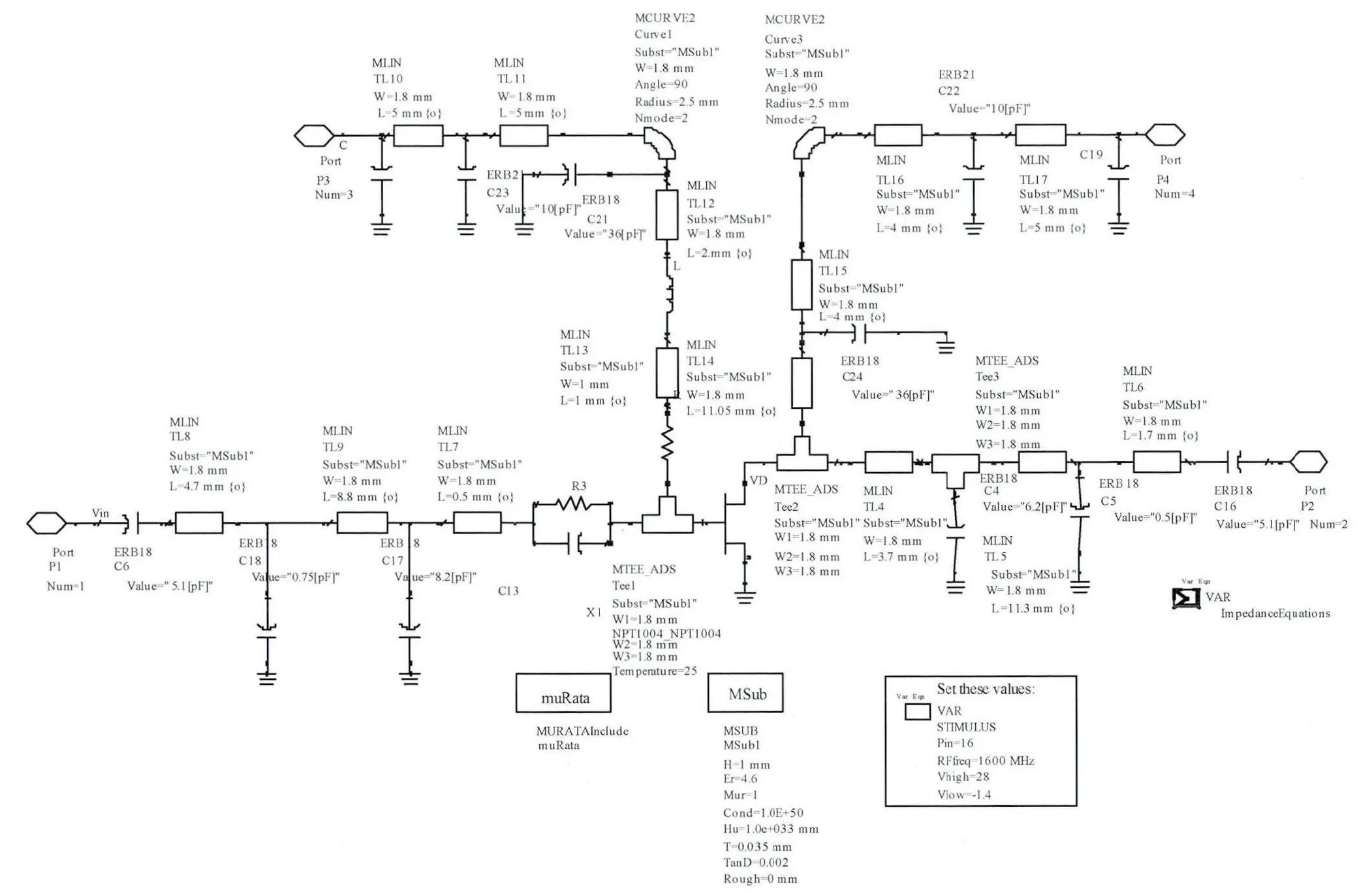
图5 功放模型内部电路原理

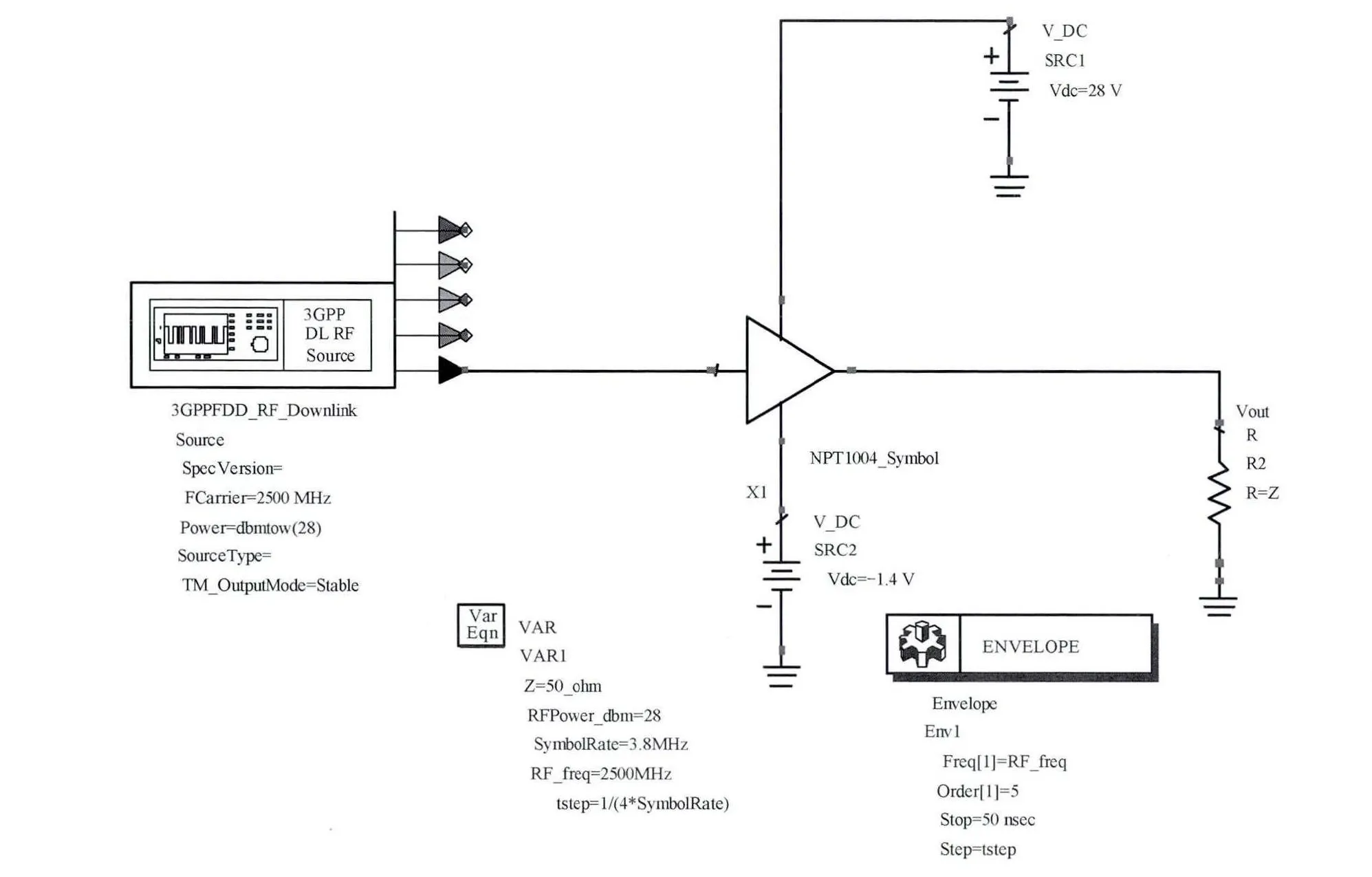
图6 功放数据的测试电路

使用3载波的WCDMA信号作为测试信号，利用包络仿真提取出功放的输入输出数据。共提取10 000组数据，其中5 000组数据用于模型参数的辨识，另外5 000组数据用来验证模型的精确度。改进的Hammerstein模型中共有4个FIR滤波器，每个滤波器含有3个抽头。使用预失真器参数离线辨识的方法得到静态的AM／AM和AM／PM特性表，利用最小均方误差（LMS）来获取模型参数。

图7所示为使用增强的Hammerstein模型、本文的Hammerstein模型对功放分别进行预失真处理得到的效果图。可以看出，相比增强的Hammerstein模型，使用本文改进的Hammerstein模型对功放进行线性化不仅补偿了由于STM而产生的带内失真，而且也抑制了由于LTM而产生的带外的频谱再生。更接近功放真实的功率谱密度曲线，建模精度更高。

图8是分别采用2种模型预失真后的AM／AM和AM／PM特性对比。由仿真结果可以看出，2种模型预失真后，线性化均有了一定的提升，由强记忆效应作用产生的发散状态都得到了改善。但是使用本文改进的Hammerstein模型建立的预失真模型进行预失真，AM／AM特性和AM／PM特性优于增强的Hammerstein模型。

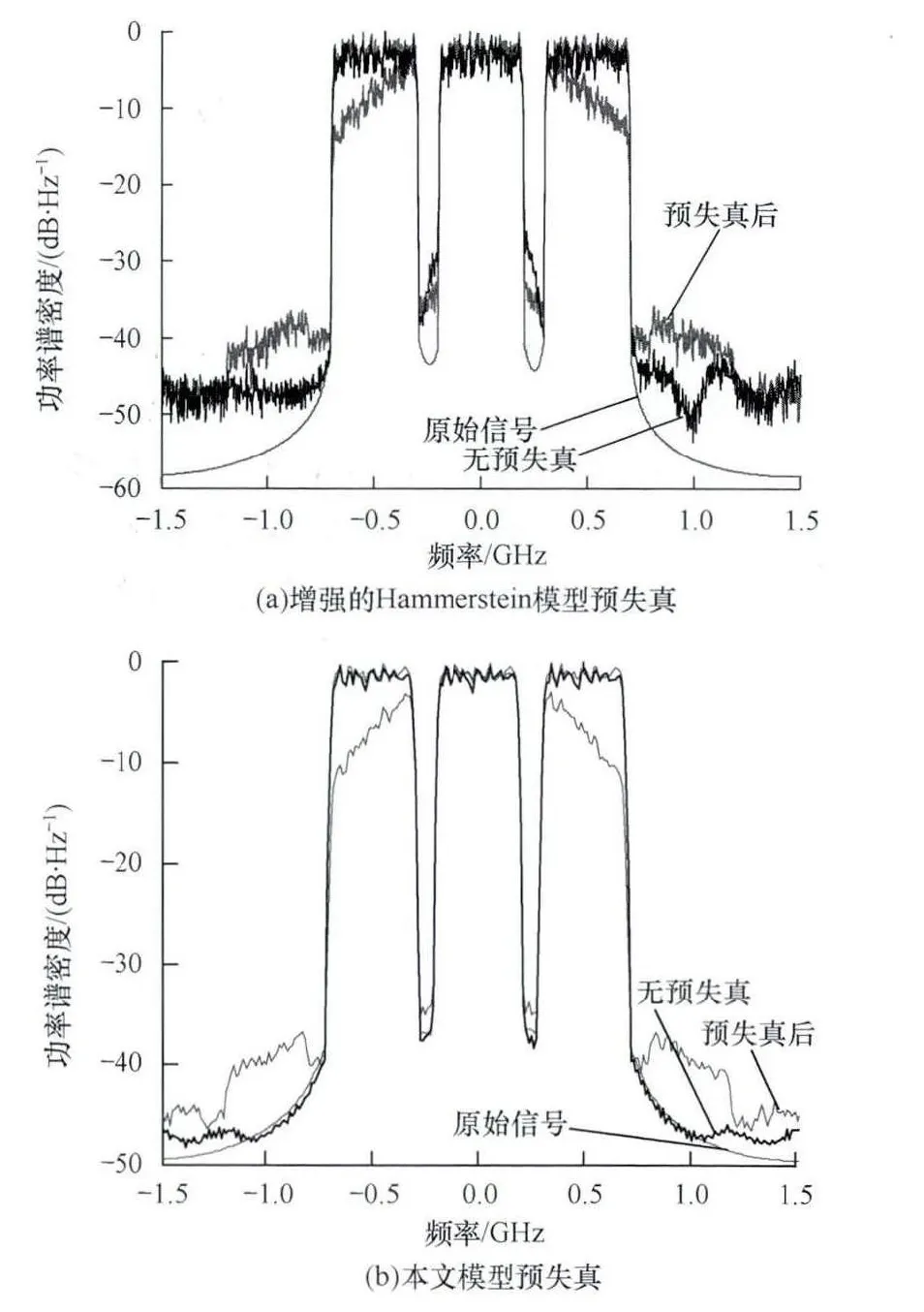
图7 2种模型预失真后效果图对比

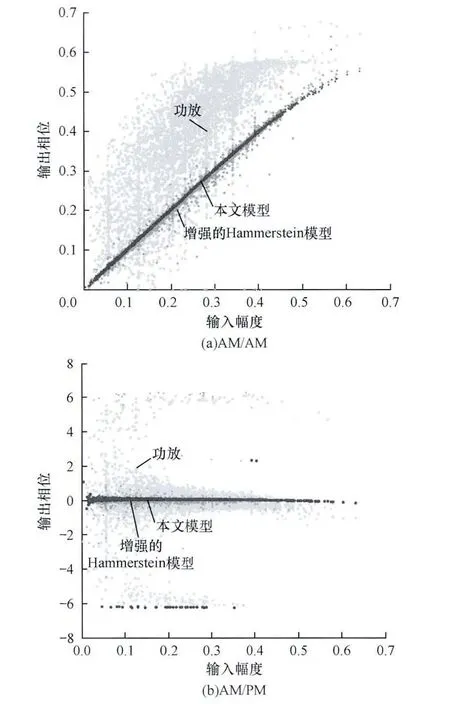
图8 2种模型的AM／AM，AM／PM特性

6 结束语

记忆效应是继非线性之后又一个限制预失真技术发展的重要领域，对其进行深入的研究具有重要意义。本文延续了Hammerstein模型的建模思想，着重考虑记忆效应对整个模型建模的影响，将Hammerstein模型中的记忆效应子系统分为弱记忆效应模块和强记忆效应模块，对两者分别建模。同时，构建附加路径从而保证了模型的精确度，达到了精确建模的目的。仿真结果表明，本文改进的Hammerstein模型在功放建模和预失真应用中都有着优越的性能。下一步工作将进一步改善功放行为建模方案，尤其是针对功放中出现的长期记忆效应进行建模，提高模型精度。

［1］Mkadem F，Fares M C，Boumaiza S．Complexityreduced Volterra Series Model for Power Amplifier Digital Predistortion［J］．Analog Integrated Circuits and Signal Processing，2014，79（2）：331－343．

［2］李诗雨．OFDM数字预失真系统自适应算法与模型研究［D］．葫芦岛：辽宁工程技术大学，2013．

［3］佀秀杰，金明录．一种新的用于 Hammerstein预失真器的自适应结构［J］．电子与信息学报，2011，33（6）：1345－1349．

［4］江 涛．Hammerstein模型辨识算法的研究［D］．西安：西安理工大学，2010．

［5］都天骄．强非线性宽带功率放大器的建模与预失真方法研究［D］．北京：北京邮电大学，2013．

［6］Lee M W，Kam S H，Jeone Y H．Split Angmented Hammerstein Model with Neural Network for a Three－stage Doherty Power Amplifier［J］．Microwave and Optical Technology Letters，2011，54（1）：124－126．

［7］叶 焱，刘太君．改进型Hammerstein动态非线性模型的Doherty射频功放线性化［J］．微波学报，2009，25（1）：55－59．

［8］南敬昌，曲 昀，王 鑫．分裂增强型Hammerstein模型的研究［J］．计算机应用研究，2012，29（12）：4703－4705．

［9］都天骄，于翠屏，刘元安，等．一种有效的基于宽带功率放大器强记忆效应特性的PMEC预失真方法［J］．电子与信息学报，2012，34（2）：440－445．

［10］Cadenas C C，Tosina J R，Madero－Ayora M J．A New Approach to Pruning Volterra Models for Power Amplifiers ［J］．IEEE Transactions on Signal Processing，2010，58（4）：2113－2120．

［11］Ngoya E，Quindroit C，Nébus J M．On the Continuoustime Model for Nonlinear－memory Modeling of RF Power Amplifier［J］．IEEE Transactions on Microwave Theory and Techniques，2009，57（12）：3278－3292．

［12］Cui Ping，Liu Yuan’an，Li Shulan．Step Memory Polynomial Predistorter for Power Amplifiers with Memory［J］．Journal of Southeast University：English Edition，2009，25（3）：303－308．