脱层缺陷夹层板的自由振动与运动响应研究

杨心怡，叶仁传，沈超明

（江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003）

0 引 言

自20世纪40年代的玻璃纤维增强塑料面世以来，复合材料产业发展迅猛。近年来，多种新型复合材料以其优良的力学性能，在船舶和海洋工程领域得到了广泛的应用[1]。其中，在两片金属面板中间填充弹性体芯材而形成的三明治结构的夹层板[2,3]，具有结构简单、自重轻、强度比和刚度比大、抗疲劳、防火及减振效果好等诸多优点。由于现有的常规船用钢材耐磨性能较差[4]，而其对温度场的变化较敏感也会影响到整体船舶建造的精度[5]；其次，采用传统钢材建造的船舶结构通常只能以加固受载部位的方式来处理冲击载荷或爆炸载荷问题，而这将极大地增加船舶质量，同时带来诸多其他负面影响[6～8]；故国外已有很多机构及公司开展了夹层板在船舶与海洋工程领域的应用研究与实践。其中，英国IE公司开发的钢/聚氨酯夹层板已经应用在船舶与海洋工程结构的建造和维修中，并以其优越的性能受到美国海军的高度重视，也获得了英国、德国和挪威船级社的认可。作为 21世纪重要的工程材料，夹层板的应用越来越广泛，尤其是在舰船上的应用呈明显上升趋势[9]。然而，此类夹层板的面板和芯材连接通常采用黏结方式，因此在制造和应用的过程中容易出现脱层和开裂等结构损伤[10]。若不能及时对脱层情况进行评估，极易造成安全隐患。

关于完整夹层板的动态响应行为已被广泛研究，而关于脱层夹层板结构的动态力学响应问题虽然起步较早但进展缓慢，目前关于夹层板脱层的研究资料较为匮乏。早在1976年，Kachanov[11]就注意到由于脱层引起的复合材料结构的破坏问题，Simitses等[12,13]考虑非线性变形，重新计算了脱层梁最大承载能力，详细研究了脱层位置、尺寸和厚度对极限载荷的影响。Hong和Chen[14]在分层区上下子板间构造一种特定的界面连接单元，以防止分层处子板间的嵌入现象，且利用时域直接积分法，对稳态激励下层合板的响应特征进行的研究，为含层间分层损伤层合板的动力分析提供了一个有效方法，以上均通过理论方法对脱层行为进行研究，虽然能够对脱层夹层板的动态力学性能进行基础的分析，但均不够系统。随着有限元技术的发展，对许多以前无法研究的问题提供了一种切实可行的方法，2012年V.N.Bur layenko等[15]首次应用有限元软件ABQUAS研究了一种存在脱层区域的四边简支板在谐振激励荷载下的部分动态响应问题。

在分析动力学微分方程和数值求解方法的基础上，通过有限元软件ANSYS/LS-DYNA分析了脱层对整体夹层板的自由振动以及在谐振荷载激励下脱层区域对夹层板运动响应的影响，并基于脱层夹层板相对于完好夹层板的运动响应差异，给出了一种识别夹层板是否存在脱层情况的新方法。

1 有限元理论公式

对中心存在圆形脱层情况的矩形板在随时间变化的载荷下的运动响应作研究。脱层区域位于上下表面黏结处，其半径为R。脱层板在外力作用下的动态响应是非线性的，即使是在小位移和最简单的线性本构关系的情况下亦是如此。

1.1 弹性小变形动力学基本方程

线弹性小变形动力学动力基本控制方程[16]组如下：

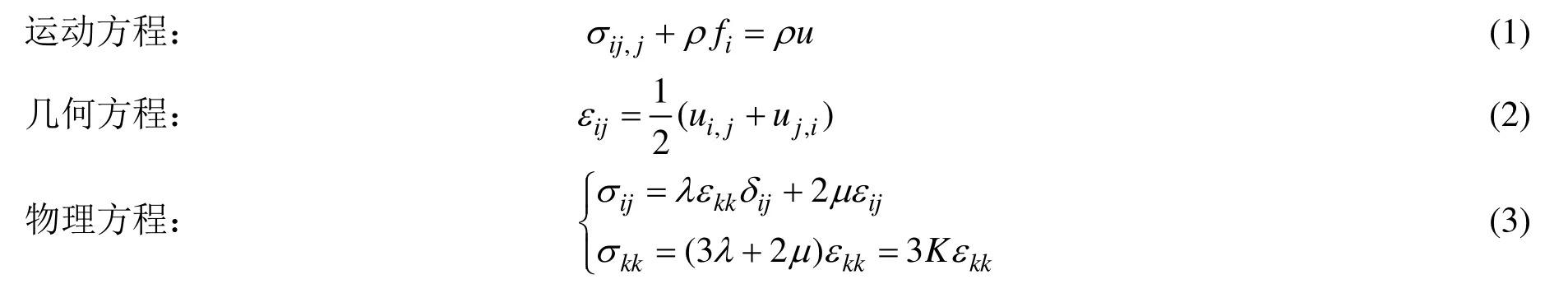
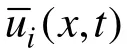
由于上述微分方程无法求解出一般性的解析解，因此只能通过数值方法求解所需的未知量。

1.2 弹性动力学数值计算方法

弹性动力学的数值计算方法是基于Hamilton变分原理，Hamilton变分原理的表述为：在一切可能的运动状态中，真实状态满足式（5）的驻值条件：

将K与U代入（5）式，并应用散度定理可得：

应用有限元法直接计算泛函数驻值是将结构空间离散化，在离散化的单元以及节点上进行位移插值，即

式中：NI——节点I的形函数。

将几何方程与物理方程写成矩阵形式为：

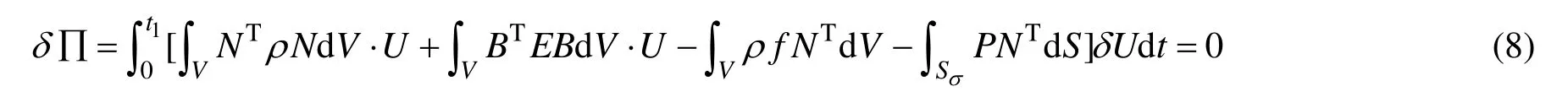
式（9）即为经过有限元离散化后获得的关于结构动力响应的二阶常微分方程，将阻尼项引入动力学微分方程可得：

2 脱层夹层板的数值仿真

2.1 矩形夹层板参数与有限元模型

夹层板脱层区域位于矩形夹层板的中心，假设脱层区域形状为圆形。矩形夹层板的平面尺寸为1m×1m，上下面板采用相同材质，详细的物理、几何参数见表1。

表1 夹层板的物理参数、几何参数

几何模型与有限元模型见图1，夹层板模型的上下面板和芯材均采用SOLID164单元，全部实体采用扫略网格划分法，脱层区域位于面板的中心且假设脱层发生在上面板与芯材黏结面，其他区域完好；由于一般夹层板的脱层面积是变化的，为研究方便，取脱层半径为R=0.1m，即脱层面积占面板总面积的3.14%，对于其他脱层面积可用相同的分析方法，面板与芯材之间的脱层区域运用面面自动接触，其余未脱层的区域的面板与芯材共节点。夹层板四周约束条件为：四边简支约束，其数学表达式为：

载荷为谐振载荷位于上面板上表面中心节点处，大小为F(t)=Fsin(ωt)，结构在受动载荷时的动态响应不仅与结构的本身固有特性有关，还与外载荷的激励频率密切有关，因此分析选择5个不同的激励频率，其值依次为：250Hz，500Hz，1000Hz，1500Hz，2000Hz且幅值均为10kN。重点分析见图1的P1、P2、P3、P4节点。

2.2 模态分析

有限元模态分析是建立模态分析模型并进行数值分析的过程，模态分析的实质就是求解有限个自由度的无阻尼弹性系统方程。

运用体单元建立的有限元的模型见图1，脱层区域运用无摩擦接触，其余接触部分采用固结形式。运用Block-Lanzos方法对完好的夹层板和脱层情况的夹层板有限元模型进行解析模态计算得到前20阶的自振频率（见表2）。

图1 夹层板有限元模型及脱层区域特征分析位置

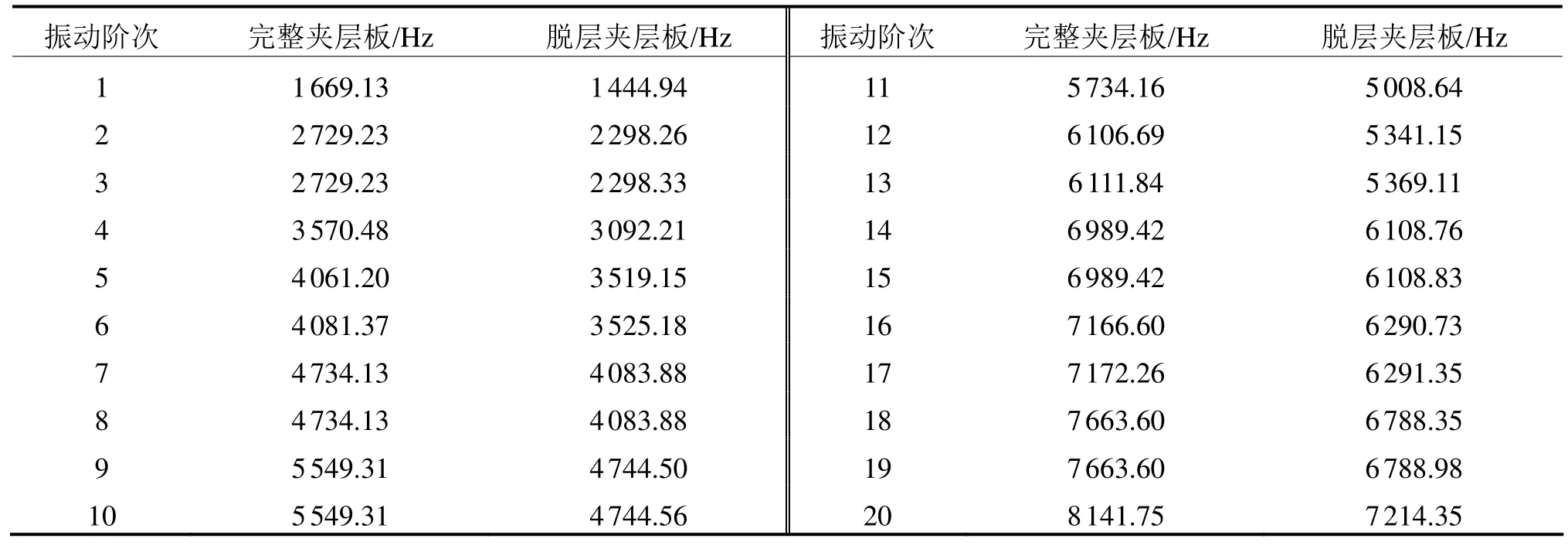
表2 完整夹层板和脱层夹层板的自由振动频率

图2 完整夹层板和脱层夹层板的自振频率对比

从图2（a）、（b）可知，在脱层面积占面板总面积的3.14%时，相同阶数下完整夹层板的自振频率均高于脱层夹层板，而且差值的变化范围均在11%～16%之间，因此可以根据完整夹层板的自由振动频率推测出夹层板在中心区域脱层面积为3.14%时各阶自由振动频率的大致范围。

2.3 谐振载荷下夹层的运动特性

一般进行动力学分析前需对结构进行模态分析，以确定结构的自振频率，从而避免结构的设计载荷频率与自振频率相同或相近而发生共振。

针对完整和脱层两种夹层板上4个代表性节点（见图1）进行不同频率下谐振载荷的动态响应分析得知，两者的P1点在不同频率下的横向位移历程曲线见图3，由图中波形周期推算出的结构响应频率与所施加的激励频率（分别为250Hz、500Hz、1000Hz、1500Hz、2000Hz）基本一致。对比图3（a）、（b）可知，在相同的激励频率下，脱层夹层板在P1点的横向位移明显大于完整夹层板，而当激励频率为500Hz时尤其明显。对比表2分析可知，完整夹层板的一阶振动频率非常接近于1500Hz，由此可以确定位移突然增大是由于夹层板在一定程度上发生了共振；而脱层夹层板在500Hz频率时也发生了共振，虽然脱层夹层板的基频远大于500Hz，但仍然会发生共振，主要是由于脱层部分可以自由运动从而容易发生局部共振，因此针对脱层夹层板不仅要考虑整体的基频还要考虑局部自振基频值，就如同板架结构的加强筋会发生局部共振一样；从两条发生共振的曲线上可以明显看出其均存在一个包络线，此现象的发生是由于激励频率与结构的自振频率虽然接近但并非完全一样，中间存在一个差值，从而导致共振产生的横向位移亦呈现周期性变化。另外，对不发生共振的情况进行分析发现在载荷幅值相同的情况下，频率越大其对应的最大位移越小，其主要原因是振动频率越大其质量惯性就越大，从而导致位移幅值反而减小。

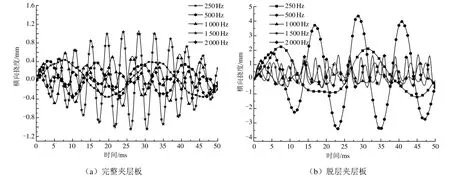
图3 P1点在不同频率下的横向位移历程曲线

由于实际设计结构时均设法使其避免发生共振，因此选取一种未发生共振情况（250Hz，1000Hz）下完整夹层板和脱层夹层板在受载荷点（P1）的横向位移见图4，频率为250Hz时完整夹层板和脱层夹层板的第一个极值横向位移分别为0.362mm和1.273mm，后者是前者的3.52倍，频率为1000Hz时完整夹层板和脱层夹层板的第一个极值横向位移分别为0.45mm和2.25mm，后者是前者的5倍，因此脱层区域受载对整个夹层板结构的危害极大。

图4 P1点相同频率下完整夹层板和脱层夹层板横向位移历程曲线

2.4 夹层板脱层识别方法

在分析完整夹层板和脱层夹层板的动态特性问题的过程中发现完整夹层板的横向位移-速度历程曲线非常有规律而脱层夹层板的横向位移曲线非常凌乱。因此，基于此结论提出了一种全新的识别夹层板是否脱层的方法。完整夹层板和脱层夹层板的4个点在1000Hz时的横向速度-位移对比曲线见图5，首先从4个点的横向位移-速度曲线可以清晰地看出完整夹层板的曲线非常有规律，均接近于椭圆且关于零点基本对称；而脱层夹层板在4个点的位移-速度曲线非常凌乱且最大正值明显高于最大负值。

由于黏结而成的夹层板较容易发生脱层且不易被侦测，根据夹层板的横向位移-速度曲线可以间接识别出夹层板是否存在脱层情况。例如，对于一块完整的夹层板要想知道其内部是否存在脱层的情况则可以在夹层板的中间某一区域施加谐振载荷或瞬时冲击载荷，然后根据测量某些特征点的横向位移-速度曲线来判断夹层板是否存在脱层的情况。此种方法检测夹层板脱层的方法机理简单、操作容易且所需的仪器和设备较少，可以用任何简便的方法来激振并测量夹层板某些特征点的位移历程曲线，然后根据特征点的位移历程曲线即可判断夹层板是否发生脱层。

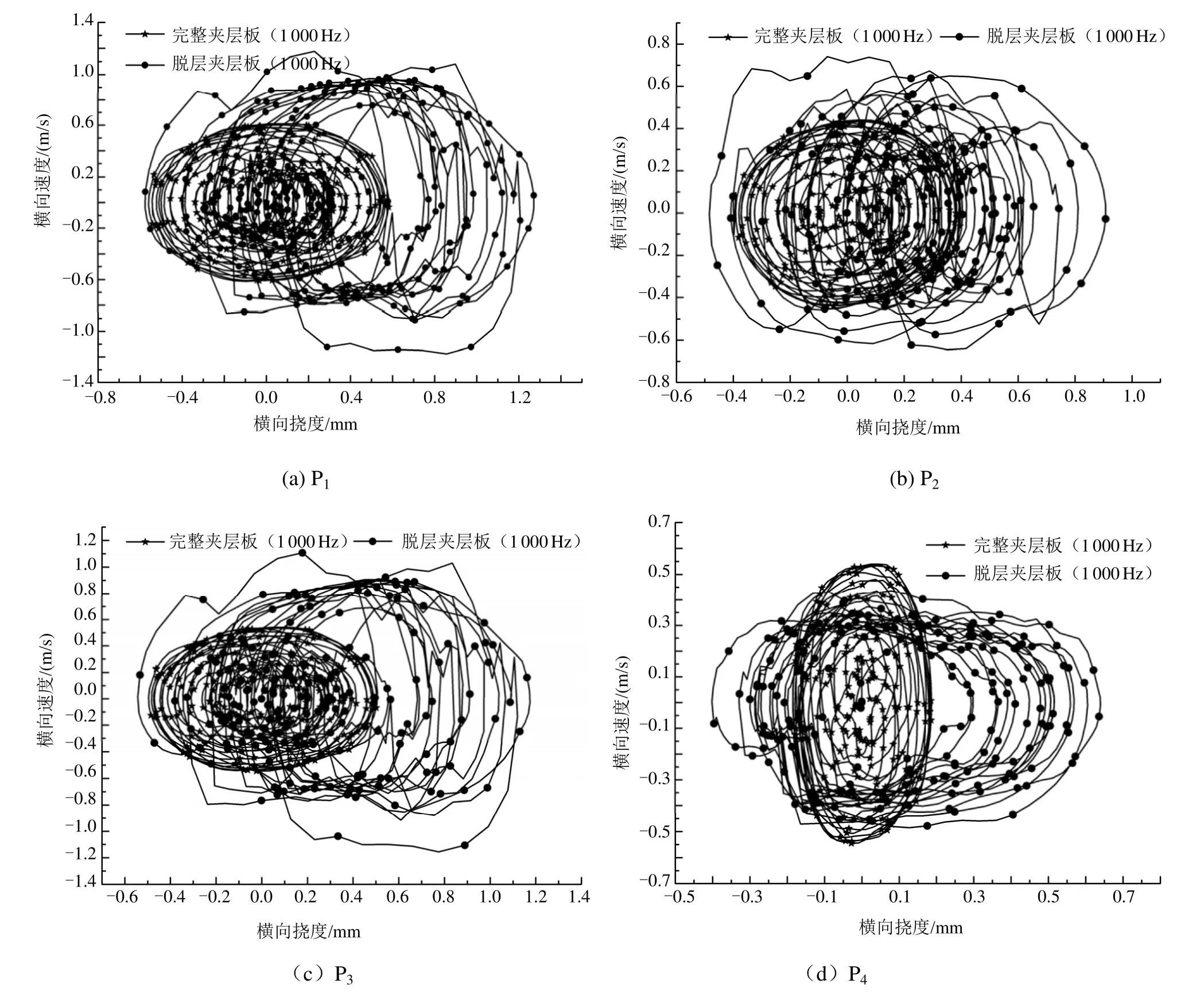
图5 相同频率下不同节点的横向位移-速度曲线

3 结 语

针对完好夹层板和脱层夹层板的情况，对比分析了完好夹层板和脱层夹层板的自由振动和运动响应变化并得出如下结论：

1) 在几何尺寸与材料参数相同的条件下，完整夹层板在20阶次以下的自由振动频率均高于存在脱层缺陷的夹层板。当脱层面积占夹层板面积的3.14%时，含有脱层缺陷的夹层板自由振动频率降低11%～16%；

2) 谐振载荷作用下（不发生共振的情况），夹层板的最大位移随谐振激励频率的增大而减小。在相同激励频率下，脱层夹层板的横向位移明显大于完整夹层板，其部分节点的最大横向位移可达完整夹层板的5倍；

3) 谐振载荷作用下，完整夹层板节点的横向位移-速度曲线均接近于椭圆且关于零点基本对称，呈现出良好的规律性，而脱层夹层板节点的位移-速度曲线则非常凌乱，不具有规律性；由此可根据夹层板的横向位移-速度曲线间接识别夹层板是否存在脱层缺陷。

[1] 白光辉. 复合材料船艇结构选型及抗爆性能分析[D]. 哈尔滨：哈尔滨工业大学，2010.

[2] Kennedy S. J., Kennedy D. J .L. A True innovation: Steel plates with a structural elastomer core[A]. Proceedings of the 5th International Conference on Composite Construction in Steel and Concrete V, ASCE, 2006:114-126.

[3] 周艳秋，洪 明. 舰船用夹层板的力学特征与应用[J]. 中国造船，2004, 45 (Sup 1): 79-85.

[4] 林海波. 疏浚系统耐磨材料的应用研究[J]. 船舶与海洋工程，2012 (4): 60-62.

[5] 杨 振，刘建峰. 温度场变化对船坞搭载精度控制的影响研究[J]. 船舶与海洋工程，2013 (3): 16-20.

[6] 顾君君，任广智，刘志良. 多桥段装船加固结构设计计算[J]. 船舶与海洋工程，2013 (3): 65-69.

[7] 汪永茂，金 军. 船舶导流管制造与焊接工艺研究[J]. 船舶与海洋工程，2012 (3): 69-73.

[8] 王 帆. 船用大型铸钢件焊接裂缝及修复工艺研究[J]. 船舶与海洋工程，2012 (4): 63-66.

[9] Rabczuk T, Kim J Y, Samaniego E, et al. Homogenization of sandwich structure[J]. International Journal for Numerical Methods in Engineering, 2004,(61):1009-1027.

[10] Luo G, Lv X. Dynamics of a plastic-impact system with oscillatory and progressive motions [J]. International Journal of Non-Linear Mechanics, 2008, 43(2): 100-110.

[11] Kachanov L M. Separation failure of composite materials [J]. Mechanics of Composite materials 1976, 12(5):812-815.

[12] Simitses G J, Sallam S, Yin W L. Effect of delamination of axially loaded homogeneous laminated plates[J]. AIAA Journal,1985, 23(9): 1437-1444.

[13] Yin W L, Sallam S N, Simtses G J. Ultimate axial load capacity of a delaminated beam-plate[J]. AIAA Journal, 1986, 24(1):123-128.

[14] Hong M, Chen H R. Dynamic behavior of laminated composite plates with delamination[J]. Ship Mechanics, 2000, 4(6): 28-38.

[15] Burlayenko V N, Sadowski T. Finite element nonlinear dynamic analysis of sandwich plates with partially detached facesheet and core [J]. Finite Elements in Analysis and Design, 2012, 62: 49-64.

[16] 金 泽. LS-DYNA3D 理论基础与实例分析[M]. 北京：科学出版社，2005.