菱形独立液舱晃荡载荷分析及强度评估研究

秦 斌，李小灵，王 冰

（江南造船（集团）有限责任公司，上海 201913）

0 引 言

随着世界航运业的发展及世界对能源需求的不断提高，超大型全冷式液化气船（VLGC）的市场需求日益旺盛，而全冷式液化气船的菱形独立液舱是该类船舶研发、设计的关键技术之一。由于全冷式液化气船营运的特性，其独立液舱需要能满足任意装载高度的要求，以满足实际营运过程中不同的装载工况需求。基于这一需求，菱形独立液舱设计过程中面临的一个重要问题就是液货舱内液体的晃荡，以及由于晃荡产生的冲击载荷。

液化气船在航行过程中，不可避免地会有液货舱部分装载的可能。对于设有C型独立液舱或MOSS型的液化气船而言，由于其液舱外形能有效引导液体的流动，发生晃荡冲击载荷的可能很小。但对于菱形独立液舱而言，当船体在波浪中运动的频率与液舱内液体振动的固有频率相近时，舱内液体将会发生剧烈的运动，在液舱边界会发生直接冲撞，并且由于菱形独立液舱内部构件较多，内部液体的运动也会对这些构件产生冲击作用。液体对液舱结构产生的冲击载荷，其特点为持续时间短，压力幅值高，在超过一定限度时，就很可能造成液舱的结构失效破坏。液舱结构发生损坏或者泄露的后果极为严重，随之而来的液体的泄漏会造成有害物质对环境的污染或引发可燃液体大火或爆炸，其后果难以想象。

液体晃荡时，由于液面的改变，对液舱周界的压力发生快速变化，同时晃荡是非常复杂的流体运动现象，它具有很强的非线性和随机性特征。即使在很小的外部激励作用下也可能发生较激烈的液体晃荡，从而导致严重的后果。

1 舱室内液体晃荡的一般特性

一般来说，舱内流体的晃荡是下面几种形式的组合[1]：

1) 驻波（Standing wave）：当液体深度h与液体晃荡方向的特征长度L之比值>0.2时易发生驻波。这种波一般会对舱顶产生冲击（见图1(a)）。

2) 行波（Traveling wave）：这种波一般发生在液体深度h与液体晃荡方向的特征长度L之比值<0.2时。行波一般对两端的舱壁产生冲击（见图1(b)）。

3) 跃波（Hydraulic Jump）：可以看出是行波的一种特殊形式，它的发生与液体与舱的振动周期的相对值有关（见图1(c)）。

4) 涡流（Swirling）——液体在舱内的旋转运动。

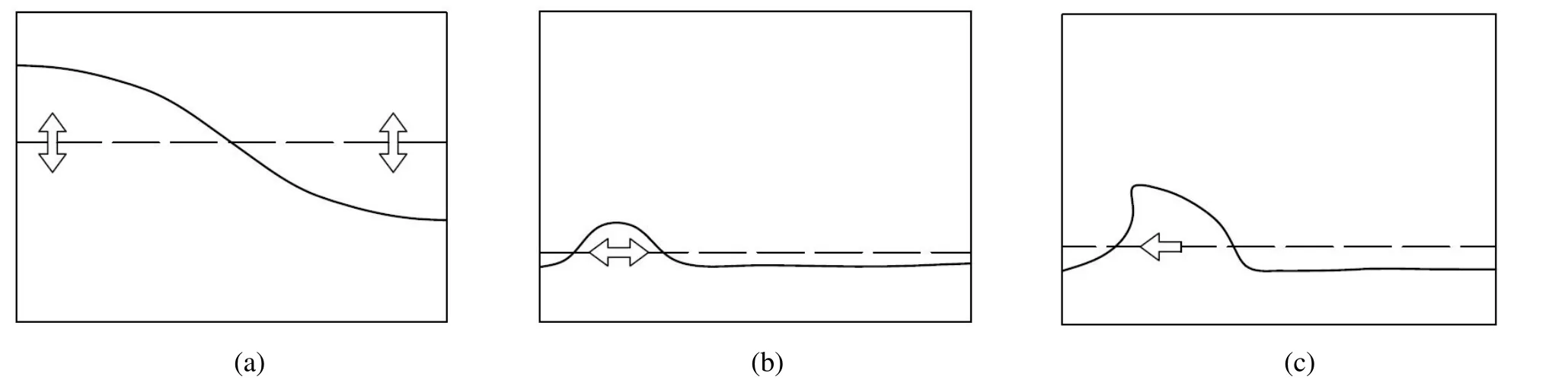
图1 波形图

由于以上各种不同形式的晃荡波形，对菱形独立液舱构件产生的载荷主要有如下几种[2]：

1) 非脉冲型动载荷，载荷在一个波形周期内发生缓慢连续变化；

2) I类脉冲型动载荷，载荷在一个波形周期内发生快速但仍然连续的变化，脉冲周期一般为波形周期的1/10左右；

3) II类脉冲型动载荷，载荷在短时间内发生突变，主要由波形与周界发生直接冲撞而产生，一般脉冲周期在波形周期的10-2～10-3左右；

4) 合成动载荷和弯矩，表征液舱周界上在一个波形周期内随时间缓慢变化的非脉冲型液压；

5) 拖曳及惯性力，主要发生在液面以下的液舱构件上；

6) 涡流导致的压力场，液体淹没的构件周围，由于压差变化与构件本身固有模态之间的差异而产生涡流导致的压力。

2 计算原理

液舱晃荡问题是典型的流固耦合问题。从问题的性质来看，它涉及相互联系、相互作用的二种不同的介质，这一特点使得它比单独讨论流体或固体结构问题时更为复杂。

流体力学描述运动的基本观点和方法有两种，即拉格朗日（Lagrange）法和欧拉（Euler）法。拉格朗日法，着眼于流体质点，设法描述每个流体质点自始至终的运动过程，通过获得流场内所有质点的运动规律来分析整个流体运动的状况；欧拉法着眼点不是流体质点，而是空间点，通过描述空间中每一点上流体运动随时间的变化情况获得整个流体的运动状况。按自由面跟踪法划分有移动网格法、标高法、MAC（Maker And Cell）法、VOF法、LEVER-SET法。目前流行的各种晃荡载荷及结构响应的直接计算的方法存在较大差异[3]。

采用LR开发程序ShipRight Sloshing，应用二维有限差分方法(液面追踪采用标记点法MAC)。该方法假定液体不可压缩、无黏性，液舱周壁刚性，内部强构件如舱壁水平桁、强框等都为刚性不可变形结构。MAC法基于欧拉运动网格，特点是在自由面上设置一组无质量的标记点，用拉格朗日运动描述标记点自由表面的节点模拟边界的大变形。

为便于分析，在保证精度的基础上，个别分析横摇与纵摇运动产生的晃荡，求解各单元所受压力的最大值，以此作为评估载荷，考察该位置板格是否有足够的承载能力。该方法基于二维计算程序，计算速度比较快。但不考虑三维效应，其对网格的数量有限制，对不规则边界的模拟不太精细，这对它的计算精度略有损失。计算研究表明，当舱内液体纵向运动固有周期与横向运动固有周期相互错开20%时，采用二维分析方法，可以保证精度。对于全冷式液化气船菱形独立液舱，在目前的设计中，液舱划分在横向一般会设置一道纵舱壁，纵摇和横摇的自由液面长度比例较大，这样在菱形独立液舱内的液体无论装载率为多少，都能够保证流体的两个方向的固有振动周期错开20%以上，所以目前大多数船研单位在研究晃荡问题时都采用二维分析方案进行晃荡仿真。

3 晃荡分析流程

当液体的固有振动周期与船体的运动周期相近时，液体运动会变得非常剧烈。船体运动时液体晃荡的外部激励，在进行液舱晃荡数值分析时，船体运动作为边界条件施加在模型上。

定义三个评估标准[2]，每一个标准要求一个不同的方法计算最大晃荡压力。

标准一（Level 1）：基于20a海况的最大船舶运动引起的静态载荷的评估；适用于船舶横摇运动周期与舱内液体横摇运动周期相互错开5s以上或是船舶纵摇运动周期大于舱内液体纵摇运动周期3s以上的情形。

标准二（Level 2）：采用最恶劣工况下的加速度计算液舱边界动态压力的评估；适用于分析当液体固有振动周期与船舶运动周期相近，装载率较低（30%左右），考察液舱四周围壁上的晃荡压力的情形。

标准三（Level 3）：采用流场有限差分程序确定液舱边界和内部结构压力评估；适用于分析当液体固有振动周期与船舶运动周期相近，高装载率，考察液舱舱顶上的晃荡压力的情形。

为防止结构失效，需用极限强度分析程序进行强度评估计算。

由于标准二、标准三均处在频率共振范围，在实际的计算中通常将标准二、标准三同时考虑，由MAC法标记液舱周界及内部构件单元，用有限差分法计算液舱周界及内部构件的晃荡压力（见图2、3）。

图2 横摇评估

图3 纵摇评估

3.1 晃荡分析流程

1) 确定评估工况下的船体特征数据（船长，型宽，型深，服务航速），运动形式（横摇、纵摇），工况（排水量，平均吃水，横稳性高）；

2) 确定评估的菱形独立液舱几何尺寸（舱长，高度，菱形折角位置），重心位置，货物密度，设定评估装载率范围及步长增量；

3) 计算出船舶横摇和纵摇固有周期，最大横摇、纵摇角，最大垂向加速度，各装载率对应的液体固有周期，并依据船体运动周期和液舱运动周期的值确定所适用的评估标准（标准一、标准二、标准三）；

4) 计算标准一、标准二各装载率下的晃荡压力，同时列出标准二、标准三各装载率对应的船舶运动数据，以此作为晃荡分析的边界条件；

5) 确定液舱围壁包括中纵舱壁及内部主要构件（强肋骨、水平桁）的构件尺寸，用MAC法求得各装载率下的晃荡压力；

6) 确定围壁及内部结构加筋板的几何尺寸，杨氏模量，屈服强度，工况（晃荡），用极限强度分析方法得到加筋板能承受的晃荡许用压力；

7) 根据评估标准一、标准二、标准三得到的晃荡压力，乘以安全系数得到实际压力，将实际压力与许用压力比较，如实际压力超过许用压力，则应修改加筋板尺寸，重复以上计算直至实际压力小于许用压力。

3.2 晃荡压力确定[2]

标准一：P=11.75(h+(Ls/2)tanθ)

式中：h——液体压头；Ls——倾角方向的自由液面长度；θ——最大横摇或纵摇角。

标准二：液舱围壁压力通过船舶生命周期内的最大横摇或纵摇角时的加速度决定的动态压力计算；

标准三：通过流场有限差分法（MAC法）计算液舱围壁压力和内部结构压力。将液舱的横剖面、中纵剖面按一定长度比例划分单元（最大不超过60×50），在液舱围壁四周及主要结构上标注单元号。给定边界条件和船舶运动工况，通过输出文件可得到每个标记单元处的压力、弯矩、速度、加速度、周期等值，即可知道液舱围壁四周的受力情况（见图4～7）。

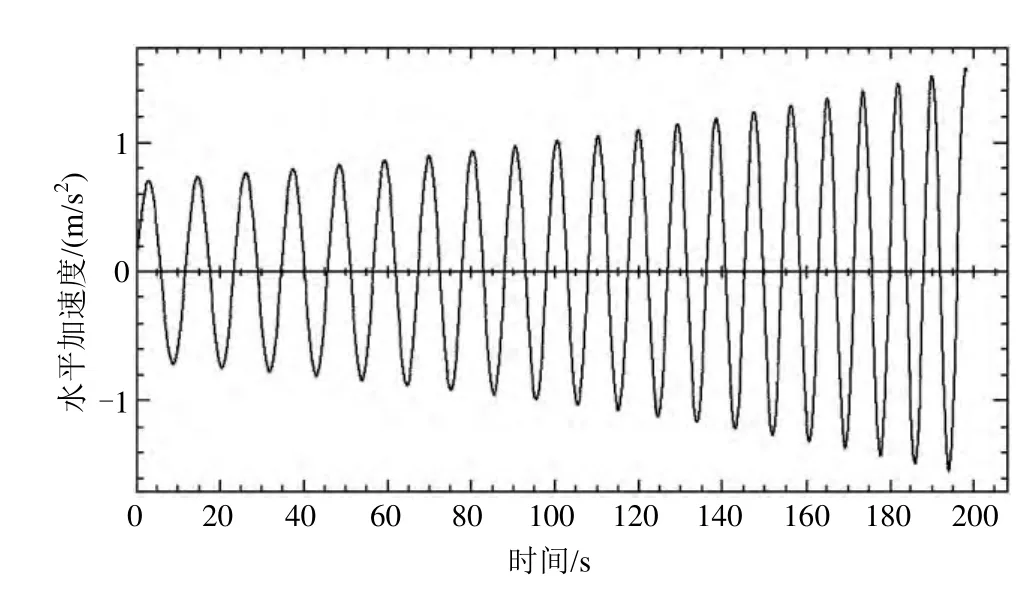
图4 某一单元处的加速度随时间分布曲线

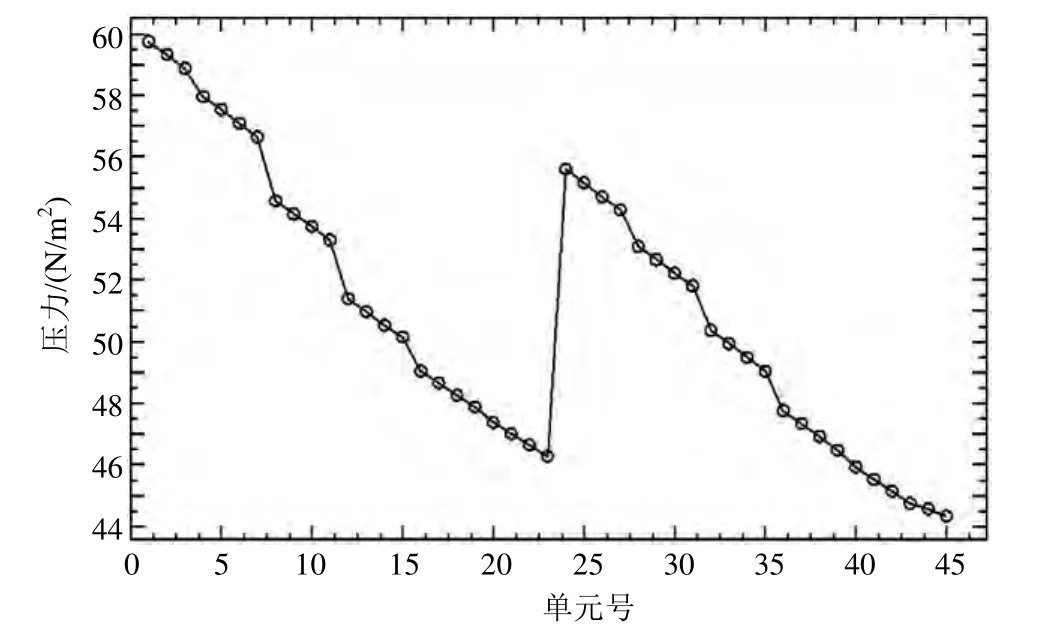
图5 某一时刻各单元处的压力值曲线

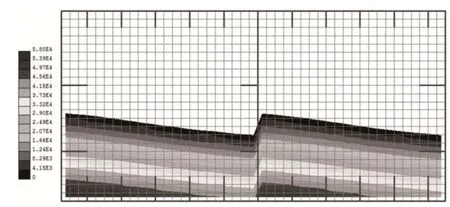
图6 某一时刻的压力分布云图

图7 某一时刻的速度分布云图

3.3 强度评估与结构衡准[3]

标准一、标准二、标准三确定了结构最大晃荡压力，将该压力乘以安全系数转化为静压力作用在结构上得到实际压力。为防止结构失效，实际压力应小于该处的许用压力。输入加筋板的几何尺寸，许用压力通过极限强度分析程序输出（见图 8）。该程序只能用于平面板架，通过设置给定的边界条件，假设板架只承受晃荡压力，计算板架在极限强度下所能承受的最大压力，即许用压力（见表1）。

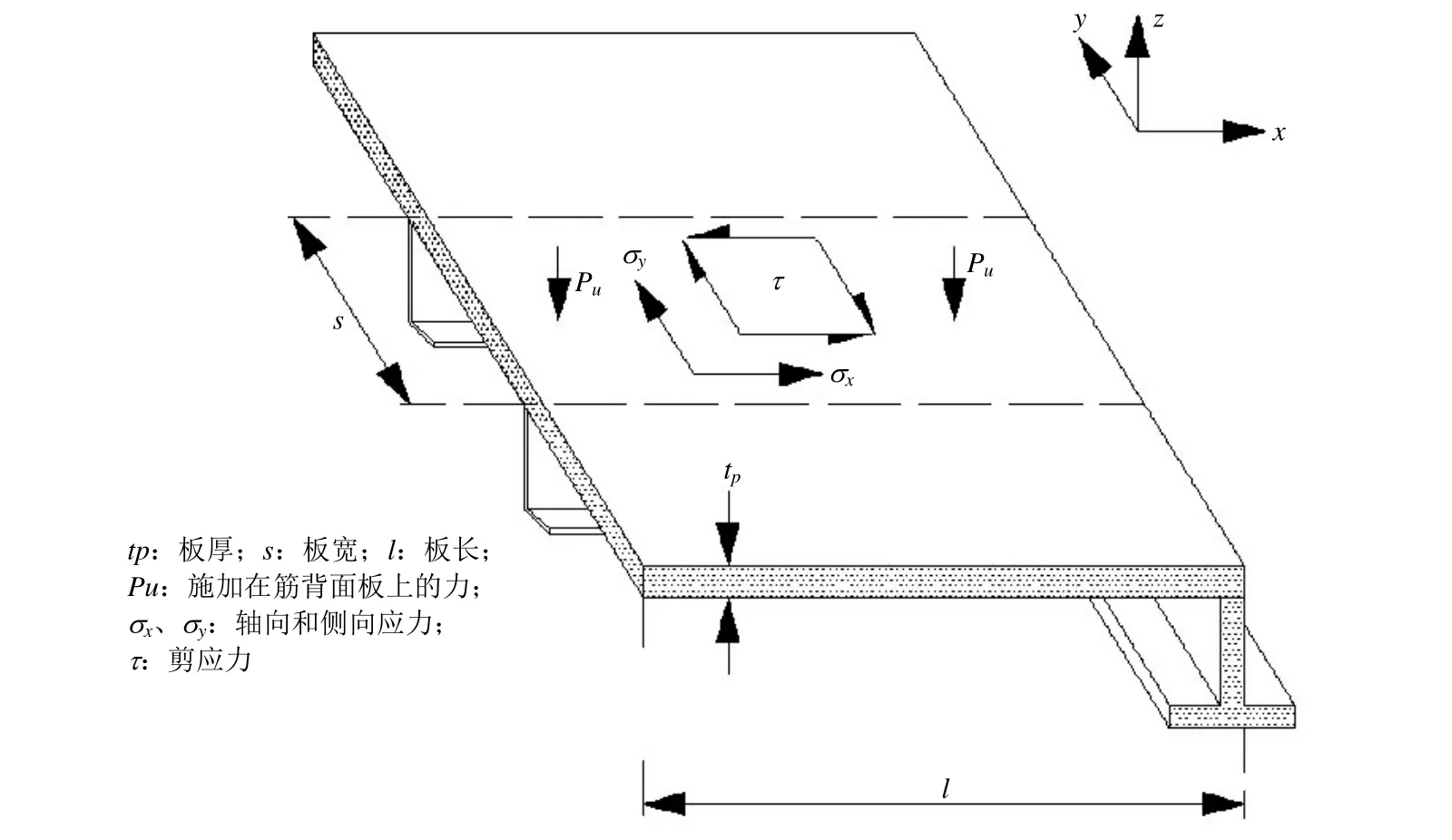
图8 加筋板几何尺寸

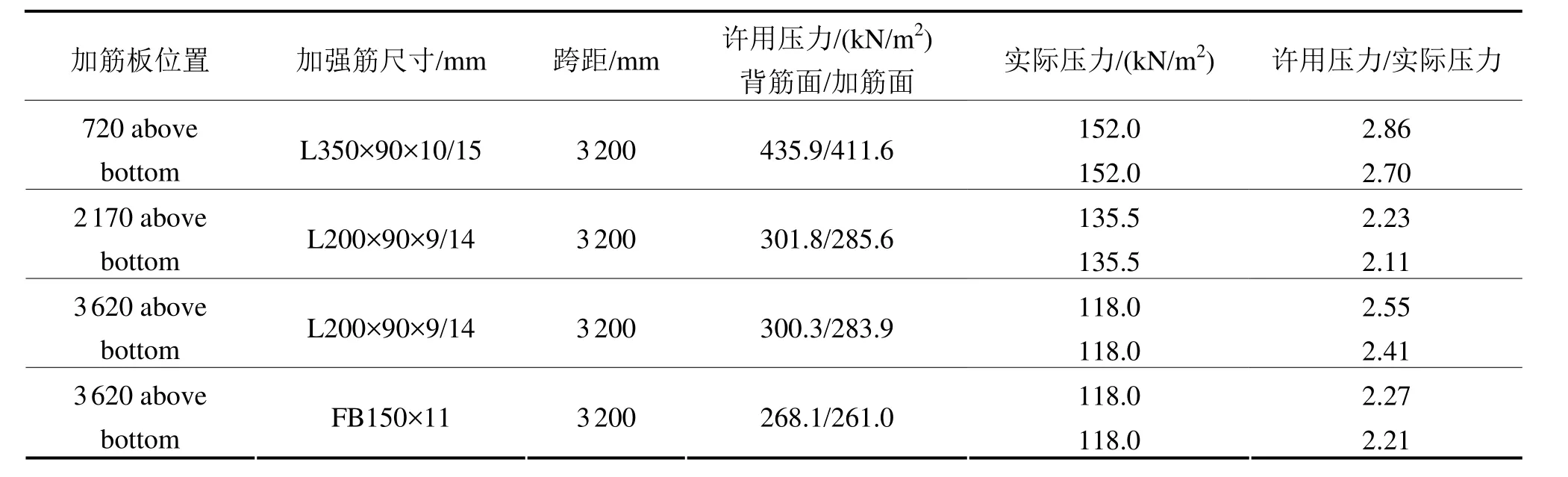
表1 某液舱晃荡压力结果评估

4 结 语

对于全冷式液化气船的菱形独立液舱而言，由于设计和衡准要求比较高，液舱晃荡问题成为菱形独立液舱结构设计和强度校核的一个关键问题。

通过对液舱内部液体运动与船舶运动相互耦合作用的评估，并借助切片理论，对舱内液体的运动状态和压力分布进行了研究，以此为基础对菱形独立液舱的结构强度进行了评估，为后期全冷式液化气船菱形独立液舱结构设计研发、优化，奠定了良好的基础。

[1] Lloyd’s Register. Rules and Regulations for the Construction and Classification of Ships for the Carriage of Liquefied Gases in Bulk[S]. 2010.

[2] Lloyd’s Register. Sloshing Loads and Scantling Assessment[S]. 2004.

[3] 娜日萨. VLCC液舱晃荡仿真及结构强度评估方法研究[D]. 哈尔滨：哈尔滨工程大学，2006.