火炬臂基座连接肘板的谱疲劳分析

李学华，李翠东，徐卜男

（惠生海洋工程有限公司，上海 201210）

0 引 言

目前对于海上油气装置生产过程中的伴生气体和泄漏气体，一般通过火炬系统将其引至船体外一定距离作放空燃烧处理，以保证人员及设备安全。火炬臂作为火炬系统的支撑结构，一端连接于主船体上，另一端则伸至空中，整个结构呈竖向或者斜向的悬臂梁状态，所以火炬臂与船体连接部分尤为关键。海上油气装置作业于固定海域，在服役期间受到风浪流等环境外力扰动而不断运动，并引起火炬臂随之运动，导致火炬臂与船体连接结构应力不断变化。火炬臂与船体连接结构的疲劳校核已经成为结构设计的关键控制因素之一。

疲劳谱分析方法相比确定性方法能够更好地考虑波浪的随机特性而在海洋工程领域广泛应用。这种方法的关键在于建立起关联环境条件和应力响应之间的传递函数，其间同时涉及水动力计算和结构计算，以及湿表面水动压力在两者之间的数据传递。由于两者计算原理和计算模型的巨大差异，要实现大量数据的自动传递将对工程软件提出很高要求。目前各大船级社开发出的软件，如SESAM虽然能够完成这一任务[1,2]，但由于投入较高，使其应用受到限制。另外，现有文献关注点集中在竖向火炬塔上部管节点的疲劳强度[3,4]，对于斜伸火炬臂基座这一特殊结构目前还未见到相关文献。

根据火炬臂受力特性，建立了火炬臂及其基座的有限元模型，并计算了校核点在横荡、纵荡、升沉各方向单位加速度下的热点应力响应。结合水动力计算中火炬臂重心位置处加速度响应的结果，组建了热点应力范围传递函数。在此基础上，根据海上装置实际运行海域的波浪散点图完成了校核点在整个服役期间的累积疲劳损伤计算。

1 水动力分析

随着计算机技术的发展, 基于三维水动力理论进行水动力分析已成为当今海洋结构物设计的主流。该理论中通常假定浮体所处的海洋是均匀、不可压缩、无粘和无旋的理想流场。因而, 流场的速度势满足拉普拉斯方程, 并满足流场自由表面和底部条件、浮体物面条件以及初始条件与辐射条件[5,6]。

海上装置在作业海域由于限位桩的限制使之方位朝向相对固定，因此不考察360°浪向下的运动响应，而是根据实际作业海域浪向分布，只确定了 3.5°和 26°浪向下火炬臂重心位置处的加速度运动响应。正常操作状态满载吃水条件下的结果分别见图1、2。为充分描述运动响应曲线规律，频率范围从0.2～1.8rad/s，间隔为0.05rad/s。

图1 火炬臂重心加速度RAO(3.5°)

图2 火炬臂重心加速度RAO(26°)

2 热点应力计算

一般来说，船体的运动和船体甲板变形是上部模块结构设计主要考虑的因素。出于环境及人员安全需要，火炬臂通常置于船首位置，即处于船体梁首端，所以船体梁载荷和甲板变形可忽略不计，只需要考虑由于船舶运动导致火炬臂所受惯性力变化引起的疲劳问题。

在Patran有限元模型中，以主甲板和艏封板为界面，并完全固定此界面上的模型节点作为位移边界条件。由于校核点位于连接肘板上趾端，距离边界有一定距离，边界条件对其影响可忽略不计。

以弦管、撑管和肘板的最小板厚t为网格边长，利用四边形网格划分连接肘板和肘板附近的部分火炬臂弦管，并在非疲劳敏感区域，使用少量三角形网格实现网格过渡。通过梁单元模拟第一层火炬臂弦管和撑管，通过壳单元模拟连接肘板和肘板附近部分火炬臂弦管，并利用RBE2单元将梁单元和同一截面中的壳单元节点相连接。

通过重量控制报告，计入火炬臂本身质量、管线、维修平台和火炬头等其他附加质量分布，将火炬臂及火炬系统整体质量模拟为重心位置处的点质量。将火炬臂重心位置处的运动视为第一层火炬臂3个节点运动的加权平均，通过RBE3单元将重心位置处的6个方向的自由度和火炬臂第一层3个节点平动自由度相连接，实现火炬臂所受惯性力向弦管节点的转移。整体有限元模型和局部网格分别见图3、4。

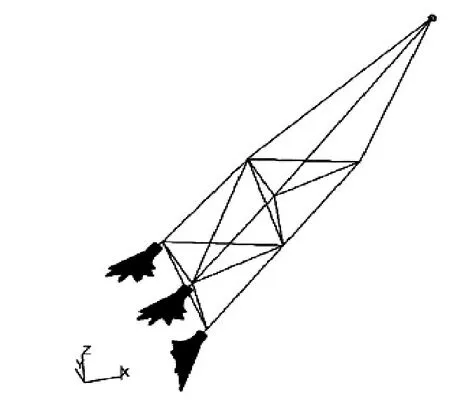
图3 整体有限元模型

图4 局部网格及目标裂纹

将单位加速度施加在各个方向，得到单位加速度下的结构应力响应。受制于篇幅，只选取图4所示目标点处的一种目标裂纹进行校核，位于强度校核中最危险连接肘板的上趾端焊缝。按照规范推荐的方法[7]，由1.5t处和0.5t处的单元表面最大主应力值向外插值得到校核点处的应力，计算结果见表1。

表1 单位加速度下热点应力 单位：MPa

3 热点应力范围传递函数组建

热点应力范围传递函数是校核点在同一浪向不同圆频率波浪作用下热点应力变化范围的集合。在火炬臂重心加速度RAO的基础上，采用将波浪诱导火炬臂重心位置加速度分量逐一作用在火炬臂重心上（谐和强迫加速度运动），计算火炬臂校核点在加速度运动激励下的热点应力强迫响应进程曲线，并计算出热点应力变化范围[8]。实际热点应力为各方向加速度引起的应力分量的合成。由于很难确定它们之间的相关系数，可按最保守的方法将它们引起的应力幅值直接相加。采用时程分析的主要优点是原理清晰并可以同时兼顾共振引起的动力放大效应，然而由于涉及动力响应分析，计算时间较长。另外，各个分量由于存在相位差，不可能同时达到最大值，将其导致应力幅值直接相加过于保守。

在本文中，通过模态分析得到火炬臂前五阶的自振频率和固有周期如表2所示。从表中可以看出，火炬臂的固有周期和船舶运动周期相差很大，故因船舶运动引起的动力放大效应可以忽略，从而可以通过静态的方法计算校核点随船体运动引起的应力变化范围。

表2 火炬臂固有周期

假定结构响应特性是线性的，在计算得到火炬臂重心位置处加速度RAO后，结合单位加速度的应力响应，通过“平方和开平方（SRSS）”法分别考虑其实部和虚部产生的结构应力[9]，即可得到不同圆频率波浪单位波幅下的热点应力幅值响应：

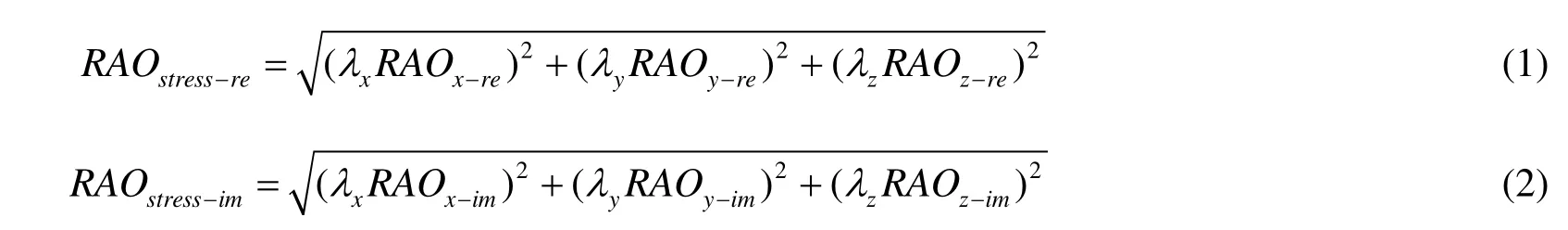
式中：λi——在i方向单位加速度下的热点应力响应值（见表1）；RAOi-re——火炬臂重心在i方向加速度RAO的实部；RAOi-im——火炬臂重心在i方向加速度RAO的虚部；RAOstress-amp——火炬臂疲劳校核点热点应力响应幅值；i表示方向的下标，i=x,y,z。

计算得到的校核点在不同浪向的热点应力范围传递函数见图5。

4 疲劳累积损伤谱分析

4.1 应力响应谱密度函数计算

应力响应谱密度函数的第n阶矩计算如下：

平均跨零周期：

图5 热点应力范围传递函数

4.2 短期疲劳损伤计算

假定每一短期海况下的应力变化过程是一个窄带的平稳正态随机过程，则其对应的应力范围分布可以用瑞利分布表示。对于具有双斜率的S-N曲线，短期海况引起的疲劳损伤可表示为：

式中：T——短期海况设计持续时间；μ——持续参数。其计算分别如下：

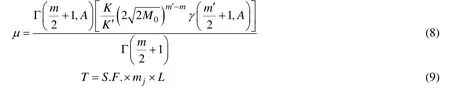
式中：K和m——空气中非管节点E等级S-N曲线高于拐点段参数，分别为 1.04×1012和 3.0；K'和m'——S-N曲线低于拐点段参数，分别为2.30×1015和5.0；S.F.——疲劳设计安全系数，根据规范取5；L——结构服役期限，文中为30a；mj——短期海况j在整个服役期所占比例；Γ(χ+1)——完全伽玛函数；Γ(χ+1,υ)——不完全伽玛函数；γ(χ+1,υ) =Γ(χ+1)-Γ(χ+1,υ)：

式中：SQ——S-N曲线拐点处的应力范围值。

4.3 长期累积疲劳损伤计算及结果

长期累积疲劳损伤计算如下：

校核点疲劳校核部分参数及最后结果（见表3）。

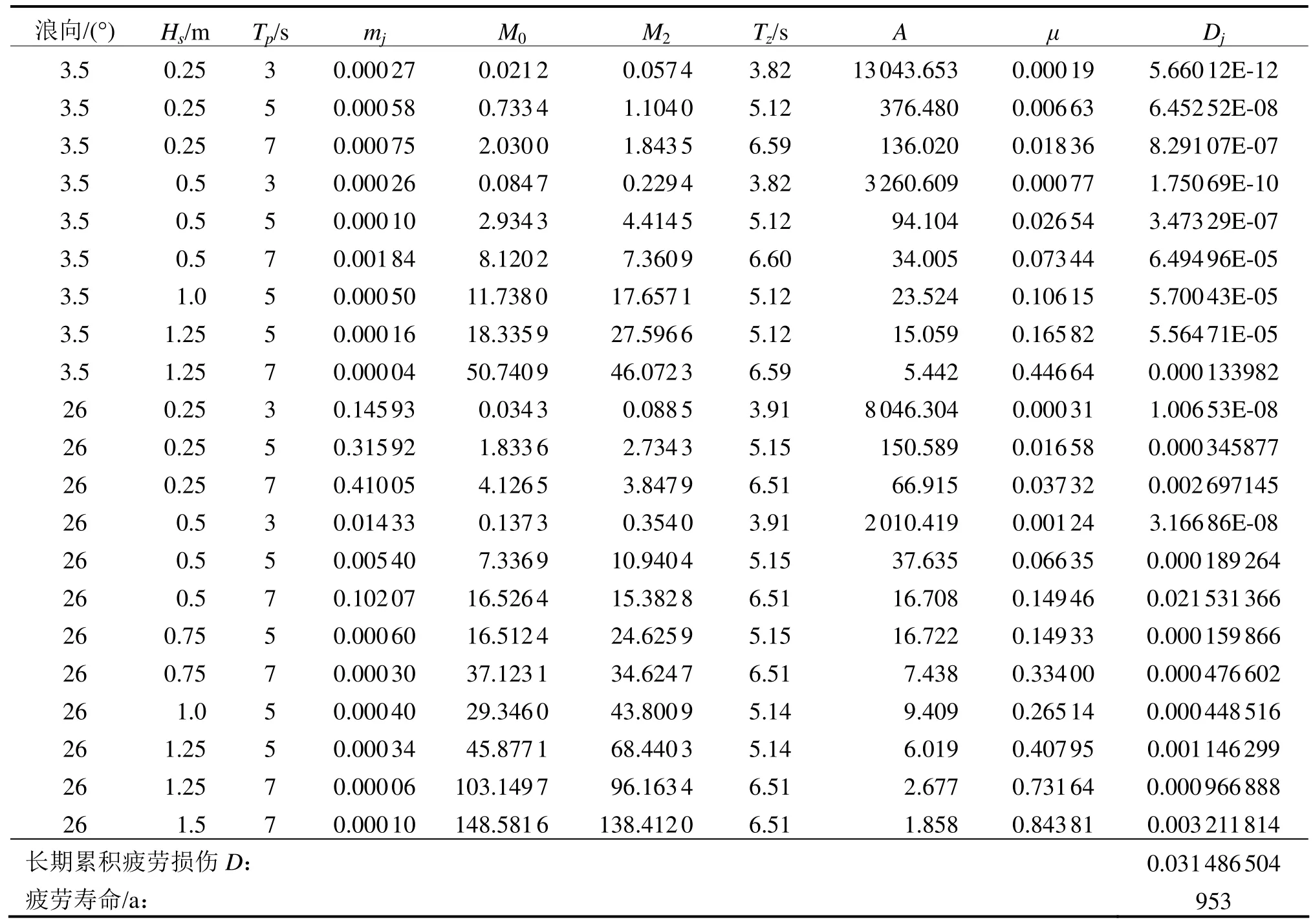
表3 长期累积损伤及疲劳寿命计算

5 结 语

通过计算火炬臂重心位置处的运动响应，结合单位加速度下的有限元分析结果，组建了各个校核点的应力范围传递函数，实现了校核点的疲劳校核，并避开了传递船体湿表面水动压力这一烦琐步骤。

1) 相比模拟所有火炬臂结构，通过RBE3单元和点质量单元可以更加准确模拟重心位置，而且不会使结构刚度增加，从而保证模型中力的传递准确性，又能减少建模的工作量；

2) 组建应力范围传递函数时，将加速度RAO的实部和虚部分别考虑，结合单位加速度下的结构静态响应，相比动力分析更加简单。通过SRSS方法得到不同方向加速度共同作用时的应力幅值相比将各方向加速度引起的应力分量直接相加更加合理；

3) 疲劳破坏是长期积累的过程，海上装置在生产场地完工后通过干拖或者湿拖的方法运输至作业海域。实际计算中，需要将途中各个海域中产生的疲劳损伤根据运输路径和海域划分图计算得到并考虑在内；

4) 海上装置在作业海域生产期间由于装载状态的不同可能会不同的吃水，并导致不同的运动结果。实际计算中要考虑不同装载状态在整个服役期可能出现的比例；

5) 疲劳寿命和制造工艺有很大关系，可通过增大圆弧半径将连接肘板上趾端做成软趾缓和硬点受力，或者打磨趾端焊缝减小应力集中来改善疲劳状况。计算中如何计及工艺影响有待进一步考虑。

[1] 张朝阳，刘 俊，白艳彬，等. 基于谱分析法的深水半潜式平台疲劳强度分析[J]. 海洋工程，2012,30(1):53-59.

[2] 马网扣，王志青，张海彬. 深水半潜式钻井平台节点疲劳寿命谱分析研究[J]. 海洋工程，2008,26(3):1-8.

[3] 魏行超. FPSO上火炬塔疲劳寿命及管节点强度研究[D]. 东营:中国石油大学（华东），2006.

[4] 胡志强，顾永宁，何 江. 浮式生产储油轮火炬塔结构的疲劳分析[J]. 中国海上油气（工程），2001,13(3):14-18.

[5] 张海彬，赵耕贤. 水动力分析在海洋结构物设计中的应用[J]. 中国海洋平台，2008,23(1):1-6.

[6] 童 波. 自升式平台运动性能预报研究[J]. 船舶工程，2011,33（增刊2）:168-172.

[7] ABS, GUIDE FOR THE FATIGUE ASSESSMENT OF OFFSHORE STRUCTURES[S]. 2003.

[8] 江华涛，顾永宁，胡志强. 海上石油浮式生产系统疲劳校核分析[J]. 船舶力学，2003,7(5):70-80.

[9] LIU Xiang-chun, FENG Guo-qing, REN Hui-long. Study on the application of spectral fatigue analysis[J]. Journal of Marine Science and Application,2006,5(2):42-46.