车辆主动悬架自适应模糊滑模控制研究
常 盛,王福明
(中北大学 机械工程与自动化学院,山西 太原 030051)
0 引言
所知的滑模控制可用于处理系统的非线性、模型的不确定性和外部扰动,具有较强的鲁棒性,可用来解决主动悬架随路面变化而产生的振动问题[1]。传统滑模控制方法需要系统的动态模型和设置控制器不确定约束值,在一个含有未知信息的复杂动态系统中是难以实现的。而模糊逻辑控制器只需要计算和编程能力就能进行控制行为,但模糊逻辑控制设计需要一个反复试验的过程来建立模糊控制规则,它缺乏稳定性和鲁棒性问题的分析解决方法。于是,研究人员结合滑模控制和模糊逻辑控制的优势发展了模糊滑模控制[2.3]。
1 车辆悬架系统模型
本文采用1/4主动悬架系统模型进行研究,其可简化为二自由度的动态模型,忽略轮胎的阻尼,视为弹性弹簧[4],如图1所示。
由模型得到的车辆悬架系统的振动微分方程为:
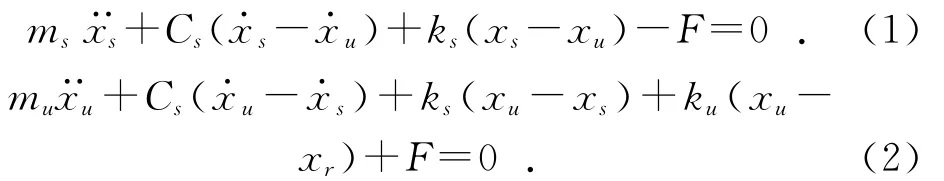
其中:mu为簧下质量;ms为簧上质量;ku为轮胎刚度;ks为悬架弹簧刚度;Cs为悬架阻尼;F为主动作动力;xu,xs和xr分别为以静态平衡点为参考位置的簧下质量、簧上质量和路面激励的垂直位移。建立状态变量X=[,xs,xu],则系统运动状态方程为:

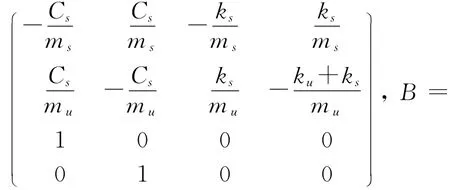

图1 1/4主动悬架系统模型
2 自适应模糊滑模控制器(AFSMC)的设计
2.1 模糊滑动面的建立
为了设计滑模控制器,将非线性悬架模型系统表示为:

其中:f(X,t)=AX为状态变量函数;g(X,t)=B为控制增益;u(t)=F为控制输入;d(t)=L为系统不确定性干扰。
控制器是让簧载质量轨迹跟踪期望模型的簧载质量变化,定义跟踪误差为:

其中:xd为期望簧载质量位移。
使用有滑动面的模糊规则,可用语句形式定义为滑动面s的控制器输入语言变量。定义的语言值为:负大(NB),负中(NM),零(ZR),正中(PM),正大(PB)。为了区分s的论域,定义如下模糊控制器的输入模糊集[5]为:

其中:为对应的模糊集,l=1,2,3,4,5.
同样定义模糊控制器的输出的模糊集为:

其中:为对应的模糊集,l=1,2,3,4,5。输入、输出模糊集的隶属度函数如图2所示。

图2 隶属度函数
条件语句形式的模糊控制规则为:

模糊集合执行模糊输入集X到模糊输出集Y的映射。令As~为X中的任意模糊集,Rl确定一个模糊集合As~◦Rl。于是根据sup-min合成推理规则有:

用xi代替的输入变量,则(xi)对应xi的隶属度函数,定义模糊基函数:

其中:i=1,2,3,4,5。
2.2 等效逼近控制
由于质量ms存在不确定性,定义:

其中:mns为参考模型簧载质量;Δm为簧载质量变化量。由于车辆受载荷的限制,设质量边界值为,满足:

根据悬架系统模型,建立一个二阶系统:
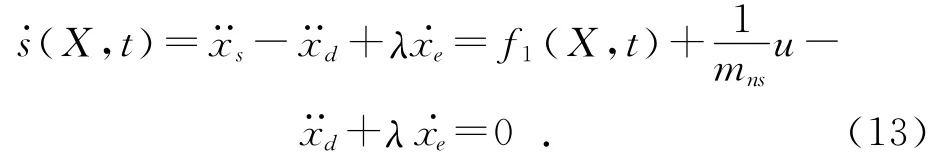
其中:f1(X,t)为f(X,t)的第2行;λ为正参数。为达到滑动面的条件,所用的控制律u设计为等效控制加上能实现对不确定性和外在干扰的切换控制:

其中:sgn(s)为符号函数;k为正常数,使系统快速接近滑动面;η是一个为实现适当鲁棒性的设计参数。
定义模糊系统逼近控制系统,即:

其中:(X|θ)=θTξ(X);θ为调节参数。
定义状态变量的跟踪误差为:

由式(13)、式(15)和式(16)得:

其中:φ=θ*-θ.
为了证明滑模控制系统达到条件,并设计调节参数θ的算法,运用一个Lyapunov函数:

其中:γ为有效学习率。由式(16)、式(17),得:

如果选择自适应律为:

则式(19)可变为:

因而滑模控制系统满足滑模存在条件,能使跟踪误差收敛。
3 仿真分析
为了验证设计的自适应模糊滑模控制器对主动悬架系统的有效性,利用MATLAB/SIMULINK进行系统的建模和仿真并对比研究。主动悬架的参数为:mns=1 314kg,mu=60kg,ks=16 000N/m,ku=1 600N/m,m~s=2 000kg;自适应模糊滑模控制器的相关数值为:γ=50,η=3 000,k=80,λ=25。其中外部路面干扰采用白噪声,建立的路面对悬架系统的时域数学模型为:

其中:q为路面位移;G0为路面不平度系数,取为6.4×10-5m2/m-1;U0为车辆前进速度;W为均值为零的高斯白噪声;f0为下截止频率,取为0.1Hz。这里假设汽车在C级路面60km/h的速度下行驶。
图3为车身的加速度轨迹误差。把自适应模糊滑模控制器(AFSMC)与传统的模糊控制器(FC)进行比较,在C级路面60km/h速度时车身垂直加速度和车轮动载荷的仿真曲线分别如图4和图5所示。
从图3可以看出,加速度轨迹误差能在较短的时间内收敛。从图4、图5中数据可知,在自适应模糊滑模控制器的控制下,最大车身垂直加速度为1.64m/s2,而在模糊控制下为3.17m/s2,在控制效率上提高了48.26%;自适应模糊滑模控制下的最大动载荷为11 374N,而在模糊控制下为18 960N,动载荷减小了40.01%。从而可以看出,自适应模糊滑模控制能在外界路面干扰的情况下有效地减小不利因素的影响,提高汽车的舒适性和可操作性。

图3 车身加速度轨迹误差

图4 C级路面60km/h速度时车身垂直加速度

图5 C级路面60km/h速度时车轮动载荷
4 结论
根据主动悬架的非线性特征,在有外部干扰的情况下,应用切换控制方法和函数逼近技术,并利用模糊语言,建立自适应模糊滑模控制器。对1/4主动悬架模型系统进行仿真,并与传统的模糊控制比较,结果显示自适应模糊滑模控制器在车身加速度和车轮动载荷控制方面具有良好的效果,改善了车辆的平稳性,使其具有良好的舒适性和可操作性。
[1]Sam Y M,Osman J H S,Ghani M R A.A class of proportional-integral sliding mode control with application to active suspension system[J].Systems Control Lett,2004,51(3-4):217-223.
[2]Chen P C,Huang A C.Adaptive sliding control of non-autonomous active suspension systems with time-varying loadings[J].Journal of Sound and Vibration,2005,282:1119-1135.
[3]Salim Labiod,Mohamed Seghir Boucherit,Thierry Marie Guerra.Adaptive fuzzy control of a class of MIMO nonlinear systems[J].Fuzzy Sets and Systems,2005,151(1):59-77.
[4]周长城.车辆悬架设计及理论[M].北京:北京大学出版社,2011.
[5]Kim Sung-Woo,Lee Ju-Jang.Design of a fuzzy controller with fuzzy sliding surface[J].Fuzzy Set and Systems,1995,71(3):359-367.

