基于多目标优化策略的框架车转向杆系优化设计

郭启涛，周云波

（南京理工大学 机械工程学院，江苏 南京 210094）

0 引言

随着工程建设的迅速发展，多轴转向车辆大量涌现［1］。对于拉杆数和轴数较多的框架车，转向时需对相当数量的车轮转角进行协调，若优化设计中只考虑车轮的转角误差最小，而忽略拉杆力，会造成拉杆力过大等不良后果，甚至还会出现拉杆损坏的情况；反之，如果只考虑拉杆力得到优化，而忽略转角误差，当误差过大时，轮胎磨损很严重［2，3］。刘从华等提出的转角误差和拉杆力同时优化的方法是以转角误差最小为优化目标，将拉杆力作为约束条件进行单目标优化［4］。本文通过对框架车转向系统的优化问题进行研究，提出了面向力和转角协调的多目标决策优化——分层序列法，并利用ADAMS对7轴车辆转向系统模型进行了优化设计。

1 面向转向杆受力和转角的多目标优化数学模型

多轴车的转向机构在进行优化分析时，一方面要求理论转角与实际转角的误差最小，另一方面要求在满足转向的要求下，拉杆力最小。同时应满足的约束条件如下：

（1）自变量上、下限约束。根据实际要求，自变量应有上、下限约束，即：

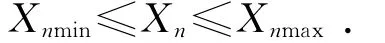
（2）结构运动特性条件。当车轮转角从最小变成最大时，油缸伸缩比须满足：

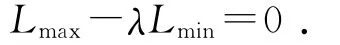
其中：λ为油缸伸缩比；L为油缸伸缩量。

（3）力约束。设Fn为第n个拉杆力，Fnmax为约束上限，则不等式约束可以表示为：

对于上述优化问题，采用多目标优化方法。分层序列法是多目标决策优化方法众多算法中的一种，根据各分目标函数的重要程度，在第一个分目标求出最优解之后，将其作为一个约束条件，加入到问题的约束集合中去，然后再对第二个分目标求解，以此类推，直到求出最后一个分目标的解，该解就作为多目标问题的最优解［5］。

1.1 优化变量

转向梯形的运动在转向行驶中起着至关重要的作用，当整车总体参数确定后，影响转向车轮转角关系的因素即为转向梯形底角和梯形臂长，同时影响拉杆受力的因素则为各拉杆的位置。而转向拉杆与蝴蝶板、转向节臂的连接位置均对上述因素有影响，故本文将它们的连接位置作为设计变量，优化设计变量为：

其中：xi1，yi1分别为第i（i＝1，2，…，6）根拉杆左侧连接点的横、纵坐标；xi2，yi2分别为第i根拉杆右侧连接点的横、纵坐标。

1.2 目标函数

1.2.1 转向杆受力

本文中的框架车是通过油缸的伸缩来实现轮胎的转向，而拉杆受力在不同伸缩量的情况下是不断变化的。图1为框架车结构示意图，图2为前油缸与拉杆之间的受力关系，其中ss′为油缸的伸长量，转向拉杆受力可完全由给定的优化变量表示，即Fn（x）＝fn（x），其中，fn（x）为各拉杆受力。

图1 框架车结构示意图

图2 前油缸与拉杆之间的受力关系

1.2.2 转角误差

在车辆行驶过程中，为减少轮胎磨损和行驶阻力，车辆在转向过程中所有轴应交于一点。本文中只考虑对框架车前半部分进行分析优化，令第i（i＝1，2，3）轴第j（j＝1，2，分别代表左、右）侧的车轮理论转角为α′ij，实际转角为αij，该车轮转角偏差为Δαij＝α′ij－αij。由于车辆转向时有不同转角，根据不同转角不同的使用频率引入如下加权函数［6］：

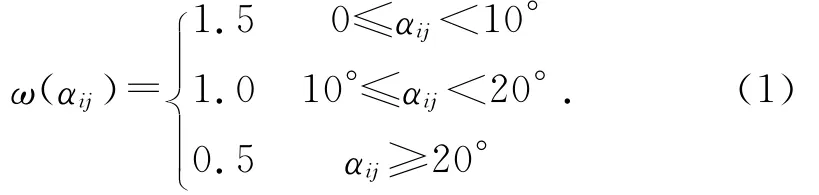
则实际转角与理论转角误差的目标函数可表示为：

2 框架车转向杆系的仿真分析模型

在ADAMS中针对7轴车辆建立框架车仿真模型［7］，如图3所示。油缸9在10s前伸长量不变，从10s开始到11s伸长量为100mm，11s后伸长量一直保持100mm，其运动时带动蝴蝶板8转动，与8连接的转向节臂带动第一轴左、右侧车轮运动，拉杆4和拉杆10带动第二轴左、右侧转向节臂运动，依次类推，从而实现各轴车轮的转向。由于该框架车前后是对称的结构，因此本文只考虑对框架车前半部分进行分析优化。

3 优化结果分析

根据分层序列法，本文将转角误差及各杆力中最大拉杆力作为首要优化目标，其他杆力在满足自身杆力约束的条件下作为次要优化目标。

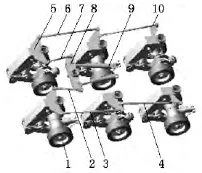
图3 框架车仿真模型

3.1 变量优化结果

利用上述优化算法优化后，对优化目标影响最大的变量的变化值见表1。

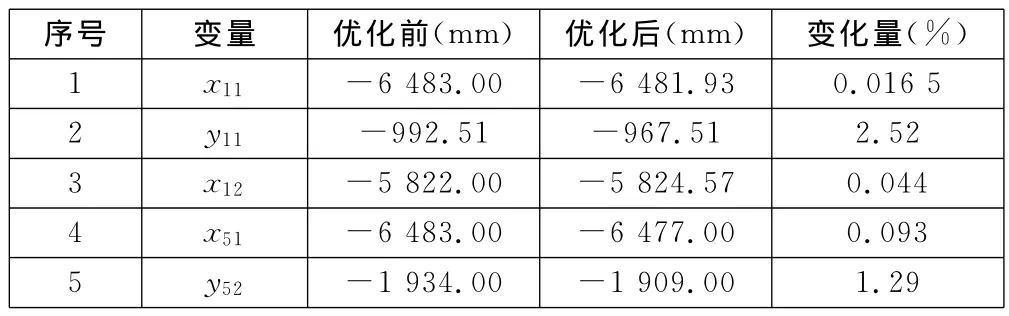
表1 优化变量结果分析

由表1可以看出利用分层序列法进行优化后，各变量对优化目标的影响程度各不相同，其中拉杆1、拉杆5与蝴蝶板、转向节臂连接位置的坐标对优化目标的影响最大，故重点对其进行了优化，以缩短优化时间，提高优化效率。

3.2 拉杆力分析

在拉杆力的计算中，通过建立拉杆力的输出通道和仿真测量即可获得各拉杆力随时间的变化关系曲线。转向时，需实时监控各转向拉杆的受力情况。转向拉杆为二力杆，其两端与其他部件铰接，因此测量转向拉杆铰接点在车辆转向平面内的合力即可得到转向拉杆的力。图4为受力最大的拉杆1优化前、后的拉杆力，表2为优化前、后各杆力对比。

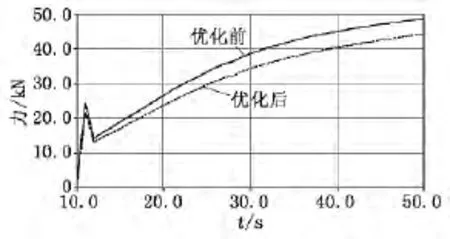
图4 拉杆1优化前、后的拉杆力

由图4可以看出，优化后拉杆1受力比优化前有了很大程度的减小，受力最大值由48 660N下降到44 264N。由表2可以看出，优化后多数拉杆力比优化前都有一定的减小，虽然个别拉杆力出现上升的情况，如第一轴外侧拉杆力从5 424N上升到6 095N，但是上升的幅度不大，且该拉杆力本身就比较小，故可得出优化后各拉杆力得到一定改善的结论。

表2 优化前、后各拉杆力对比

3.3 转角误差分析

由于车辆在转向行驶过程中会受到转向阻力矩等因素的影响，因此转向时车轮实际转角将与理论转角有一定的误差，当误差过大时，轮胎磨损将会很严重。本文中各轴车轮的理论转角是通过将一轴内转向轮的偏转角视为理想的阿克曼转角而推导得到的［8，9］。表3为优化前、后各轴转角误差对比。

表3 优化前、后各轴转角误差对比

通过表3中优化前、后各轴转角误差值，由式（1）、式（2）可以算出优化前、后转角误差目标函数分别为4.24°和2.76°，优化后各轴车轮的转角与理论转角的差值比优化前的减小了34.9%。同时可以看出，第二、三轴的左侧车轮转角优化效果最好，右侧车轮转角优化效果稍微差一点。故优化后转角误差较优化前有了较大的减小，从而减小了轮胎磨损。

4 结论

本文利用ADAMS软件建立框架车转向机构的运动学模型，在对原转向机构运动学分析的基础上，利用分层序列法，确定各目标的重要程度，并对车轮转角和杆力全程范围进行了优化，优化后的多轴转向机构转角误差减小了34.9%，同时大多数拉杆受力也得到了一定的改善，尤其是受力最大的杆件1的拉杆力较优化前有了很大的减小。由于转角误差的减小，从而减小了轮胎磨损，延长了轮胎的使用寿命，使该车的操纵稳定性有所提高。

［1］王云超，高秀华，张小江.重型多轴转向车辆轮胎原地转向阻力矩［J］.农业工程学报，2010，26（10）：146-150.

［2］王云超，高秀华，陈宁.多轴转向车辆转向杆系的受力分析［J］.计算机仿真，2009，26（12）：239-243.

［3］王翠，马力，邓小禾.多轴平板车转向机构优化设计［J］.武汉理工大学学报，2012，34（5）：573-576.

［4］刘从华，赵斌，高秀华，等.多轴转向车辆转向机构优化设计［J］.农业工程学报，2007，23（9）：81-85.

［5］徐玖平，李军.多目标决策的理论与方法［M］.北京：清华大学出版社，2005.

［6］杨新明.多轴转向汽车运动分析与仿真［D］.武汉：武汉理工大学，2003：27-28.

［7］Mohamed Kamel Salaani.Heavy tractor-trailer vehicle dynamics modeling for the national advanced driving simulator［J］.SAE Paper，2003-01-0965

［8］Babu R.Optimizing steering system design parameters of motorcycles using multi-body computer simulation［J］.SAE Paper，2002-32-1799.

［9］Zbigniew Lozia.Vehicle dynamics and motion simulation versus experiment［J］.SAE Paper，980220.