组合杂交Wilson矩形单元的加权能量正交关系
聂玉峰,张 玲,王惠玲
(西北工业大学 应用数学系,陕西 西安 710129)
随着航空航天、汽车、医疗等领域尖端技术的发展,仅研究材料的力学行为已不能够满足实际应用的需求,需要关注材料的多物理场(如热、力、电、磁)耦合行为[1-3],于是相关物理量及其空间梯度、时间变化率等的计算精度都非常重要。针对弹性力学问题,周天孝研究小组建立了组合杂交变分原理[4-5],它是稳定化的变分原理,为应力离散空间的优化设计提供了很大的便利,并成功建立了求解弹性力学问题的高性能四边形单元、六面体单元以及板单元等[6-8].在探索热力耦合问题的高性能组合杂交有限元求解算法之前,有必要探索热传导问题的有效求解算法.
当材料为各向同性,热传导问题的数学模型简化为Poisson方程,不同于文献[9]给出的结论,本文分析论证了用Wilson非协调模式增强温度函数插值所建立的组合杂交矩形元,其非协调温度插值梯度(热流)关于分片线性温度梯度插值加权能量正交,分片线性温度梯度插值的散度(热源)与非协调温度插值加权能量正交.排除舍入误差的影响,组合杂交矩形元与相应的双线性元在单元上对于温度及温度梯度数值求解结果相同.
1 组合杂交变分原理
对Poisson方程边值问题

由最小势能原理、最小余能原理出发,引入变量σ=▽u,借助区域分解技巧放松场函数在单元边界处的连续性要求,可建立两个相应的变分原理,对其直接离散需要满足LBB条件,为避免该条件并增强解的稳定性,将两个变分原理线性组合,可得到如下基于区域分解的组合变分原理:求(σ,u)∈Γ×U使得

其中,
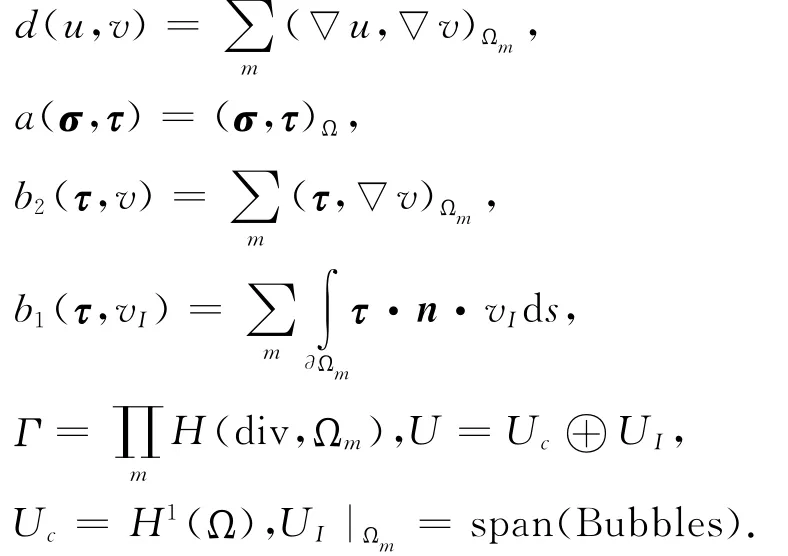
组合参数α∈(0,1),Th={Ωm}为区域Ω的有限元剖分,Bubbles表示在单元边界或部分边界上等于零的函数.
对于网格Th,令Γh,Uh为相应于区域剖分的有限元离散空间,满足Γh⊆Γ,Uh⊆U,则对上述问题有如下离散形式:求(σh,uh)∈Γh×Uh,使得


2 场函数的插值近似
对单元Ωm,设pj(xj,yj)(j=1,2,3,4)为单元按逆时针方向排列的4个顶点,Fm是从参考单元:[-1,1]×[-1,1]到Ωm的双线性等参变换

其中,Nj= (1+ξjξ)(1+ηjη)/4,(ξj,ηj)(j=1,2,3,4)是参考单元的4个顶点的坐标.
温度梯度插值函数离散空间Γh= {τ∈Γ:τ|Ωm=◦},在参考坐标系下温度梯度插值函数为

其中βj(j=1,2,…,6)为待定参数.


式(7)为Wilson Bubble,它将双线性插值丰富为完全二次多项式以提高逼近精度.
3 刚度矩阵推导

在单元Ωm上由式(4)可得

利用式(5)—(7)可计算得到
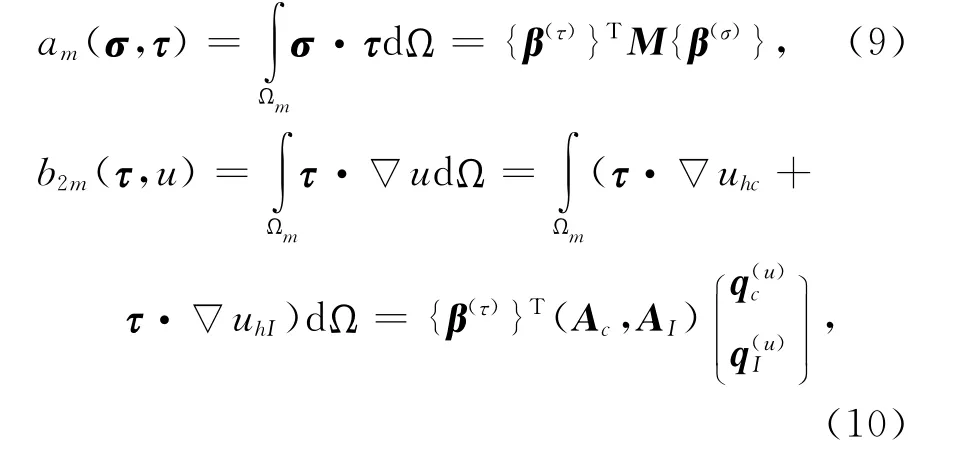

将式(9)—(11)带入式(8),得到温度梯度参数

又因为
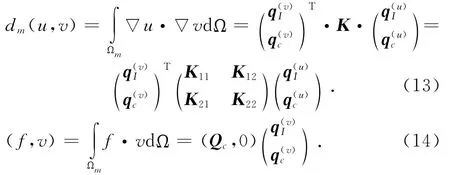
将式(9)—(14)带入式(3),可得

所以单刚矩阵

当单元为三角形时,推导过程相同,仅需替换相应的插值基函数.
4 矩形单元时的刚度矩阵分析
首先计算分析D12,对于矩形单元引入几何参数:
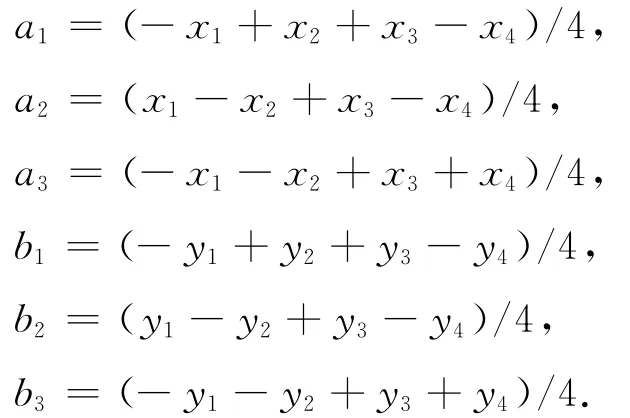
经计算可得


上式表明协调与非协调温度插值导出的梯度是正交的.进一步计算可以得到

经计算有-1AI= [0]4×2和-1BI= [0]4×2.进而得到
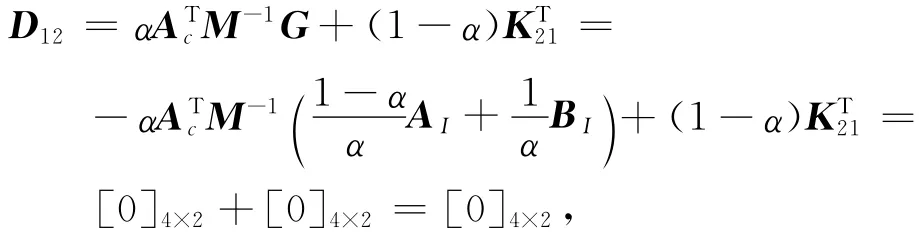
表明单元内部自由度和顶点自由度无耦合.
表达式-1AI= [0]4×2说明非协调温度插值的梯度(热流)关于分片线性温度梯度插值加权能量正交;表达式-1BI= [0]4×2则表明分片线性温度梯度插值的散度(热源)与非协调温度插值加权能量正交.
讨论D11与双线性等参元刚度矩阵K11的关系.经计算

这种组合元的温度结果与双线性参考元计算相同,后面算例也将表明这一结果的正确性.
矩形单元Ωm的4个顶点pj(xj,yj)(j=1,2,3,4)的温度值分别为uj(j=1,2,3,4),在参考坐标系下,四点温度插值基函数对ξ和η的偏导数分别为

这里,分别记∂Nj/∂ξ与∂Nj/∂η为Nj1、Nj2,其中j=1,2,3,4.
对双线性等参元,温度梯度由温度插值函数的梯度计算得到
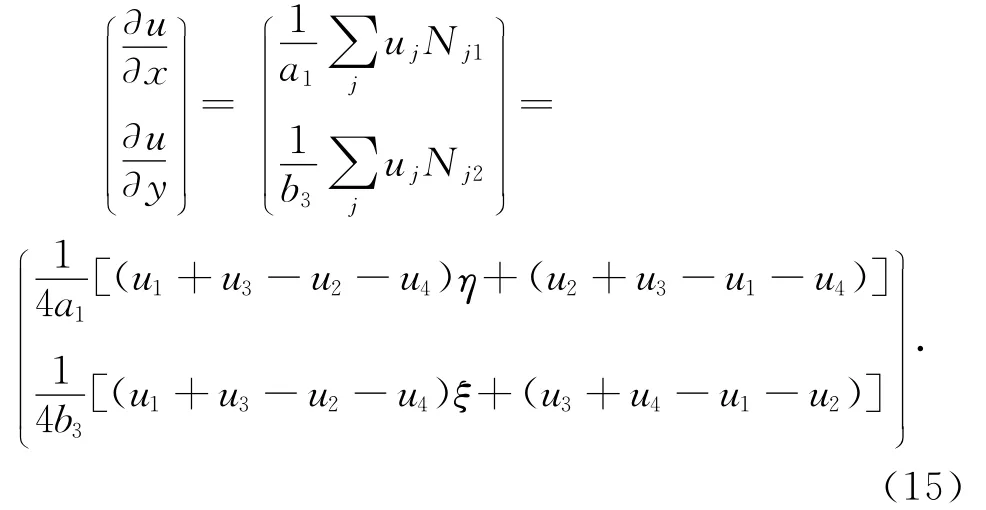


即两种方法得到的温度梯度结果相同.
综合以上结果知,当采用矩形剖分时,用Wilson非协调模式增强温度函数的插值所建立的组合杂交矩形元与相应的双线性元计算结果一致。这一结论不同于文献[6]在对弹性力学问题的求解时所给的结论.
事实上,可以证明当采用三角形剖分网格时,Poisson方程温度插值函数的协调部分span(L1,L2,L3)和非协调部分span(L1L2,L2L3,L3L1)关于分片线性温度梯度插值函数也是能量正交的,进而得到此时的三角形组合杂交元退化为三角形线性元,即有三角形组合杂交元与协调的三角形线性单元等价.这一结论与文献[10]中关于弹性力学问题的求解时所得到的结论相同.
5 数值实验
本节通过算例验证前面的分析结果,针对Poisson方程,采用文中的组合杂交元进行计算,并与双线元计算结果比较,参考点选为中心点,计算区域为[0,1]×[0,1],准确解u=x+y+x2y2,f=-2(x2+y2),剖分如图1所示.

图1 区域剖分Fig.1 Domain division
从表1和表2的数据可以看出,双线性元与本文建立的组合杂交元计算的温度和温度梯度相同.

表1 中心点温度绝对误差Tab.1 Absolute error of temperature at central point
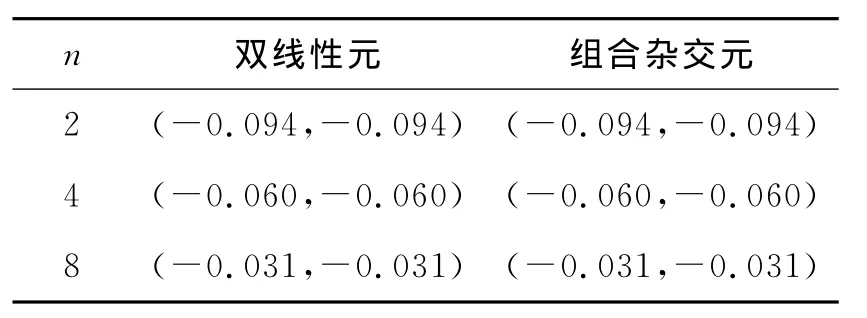
表2 中心点温度梯度绝对误差Tab.2 Absolute error of temperature gradient at central point
6 结论
对于Poisson方程,本文给出了其组合变分原理并分析论证了组合杂交矩形元的加权能量正交关系,与弹性力学问题求解所得结论不同,组合杂交矩形元刚度矩阵等同于协调的矩形双线性元刚度矩阵.当剖分单元为三角形时,能量正交关系依旧成立且三角形组合杂交元刚度矩阵等同于协调的三角形线性元刚度矩阵.要构造单元增强精度格式需着眼于突破D12=[0]4×2这个恒等关系.
[1]Chockalingam K,Wellford L C.Multi-scale homogenization procedure for continuum-atomistic,thermo-mechanical problems[J].Computer Methods in Applied Mechanics and Engineering,2011,200(1/4):356-371.
[2]Ren B,Qian J,Zeng X,et al.Recent developments on thermo-mechanical simulations of ductile failure by meshfree method[J].Computer Modeling in Engineering&Sciences,2011,71(3):253-278.
[3]Bonito A,DeVore R A,Nochetto R H.Adaptive finite element methods for elliptic problems with discontinuous coefficients[J].SIAM Journal on Numerical Analysis,2013,51(6):3106-3134.
[4]Zhou Tianxiao.Finite element method based on combination of"saddle point"variational formulations[J].Science China:E,1997,40(3):285-300.
[5]Zhou Tianxiao.Stabilized hybrid finite element methods based on the combination of saddle point principles of elasticity problems[J].Mathematics of Computation,2003,72(244):1655-1673.
[6]Zhou T X,Nie Y F.Combined hybrid approach to finite element schemes of high performance[J].International Journal for Numerical Methods in Engineering,2001,51(2):181-202.
[7]聂玉峰,周天孝.高性能八节点六面体组合杂交元[J].数值计算与计算机应用,2003,24(3):231-240.
[8]Zhou T X,Xie X P.Zero energy-error mechanism of the combined hybrid method and improvement of Allman′s membrane element with drilling d.o.f.s[J].Communications in Numerical Methods in Engineering,2004,20(3):241-250.
[9]张一凡,胡兵,王柱.Possion方程的组合杂交有限元方法[J].四 川 大 学 学 报:自 然 科 学 版,2005,42(3):467-470.
[10]聂玉峰,周天孝,聂铁军.三角形单元协调与非协调位移的能量正交关系[J].应用数学和力学,1999,20(6):619-624.

