具有Ivlev功能反应的捕食-食饵模型在零解处的分歧
吴建华,杨文彬
(陕西师范大学 数学与信息科学学院,陕西 西安 710119)
本文主要讨论以下反应扩散系统:

其中△表示Laplace算子,Ω是RN(N≥1)中具有光滑边界∂Ω的有界区域,u、v分别表示食饵和捕食者种群的种群密度.a(c)表示食饵(捕食者)种群的自然增长率,d表示食饵转化为捕食者的转化率,γ表示捕食者捕杀食饵的效率.a、c、d和γ均为正常数.系统(1)是一个具有食饵依赖关系的捕食 -食饵系统,这种依赖关系通过Ivlev型功能函数(1-e-γu)反映.这一功能函数单调递增而且一致有界,最早由Ivlev在文献[1]中提出.
数学家和生物学家对Ivlev型的捕食-食饵系统有浓厚的兴趣,同时也取得了重大的研究进展,相关成 果 可 参 考 文 献 [2-8](ODE 型 ) 和 文 献[9-11](PDE型).其中,文献[2-5]主要致力于极限环的存在性和相图的数值计算.文献[6]讨论了一类脉冲模型正周期解的存在性、稳定性以及系统的持久性.文献[7]讨论了一类脉冲模型的不稳定性和系统持久性.文献[8]研究了上(下)临界Hopf分歧的存在性及时滞对系统动力学的影响.齐次Neumann边界条件下,文献[9]通过数值计算讨论了噪音和周期外力对系统不稳定性和震荡与否的影响.在齐次Dirichlet边界条件下,文献[10]给出了系统正解存在的充分必要条件.文献[11]利用Leray-Schauder度理论和分歧理论得到了系统(1)正解存在的充分条件,并讨论了γ充分大时系统(正解)的多解性以及γ2(c+d)≤2时系统正解的唯一性.但是,文献[11]中并未讨论发自零解的小的分歧正解的存在性和稳定性.本文主要讨论系统(1)发自零解的分歧正解的存在性和稳定性.
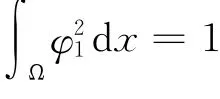
1 分歧正解的存在性
引理1[11]如果系统(1)存在正解(u,v),那么
1)(a,c)满足a>λ1,c+d>λ1;
2)(u,v)满足0<u<θa<a,0<v<θc+d<c+d,x∈Ω.进一步,若c>λ1,则v>θc.
假设p>N.定义Banach空间X和Y:

定义算子F:R×R×X→Y,
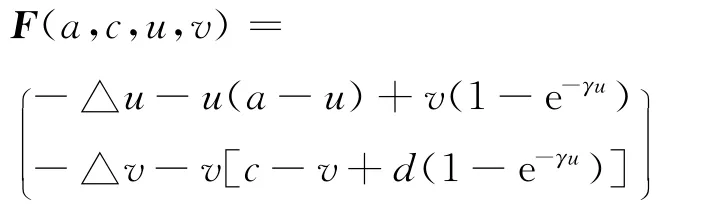
则系统(1)等价于非线性方程

则方程(2)变形为
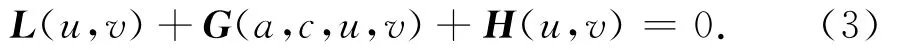
记L的核空间为N(L),L的值域空间为R(L),L的伴随算子为L*.容易验证 N(L)= N(L*)=span{(φ1,0)T,(0,φ1)T}.因此空间X和Y可以分解为



假设(u,v)∈X.由空间分解(4)可知,u和v可以表示为u=α(φ1+φ),v=β(φ1+ψ),α、β∈R,(φ,ψ)∈X2.因此,
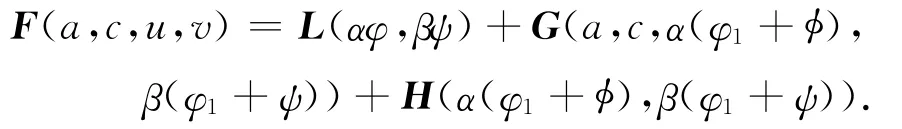
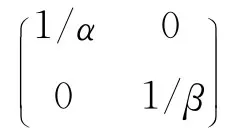
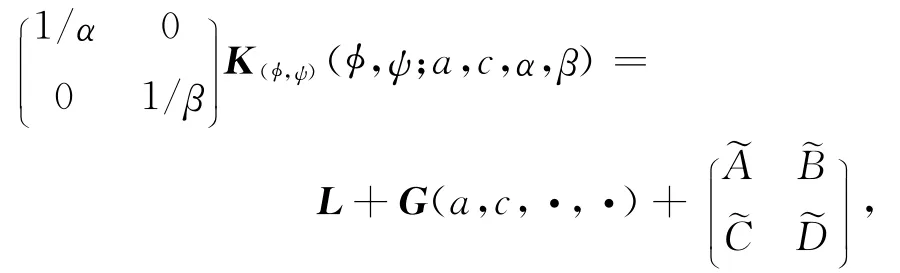
其中

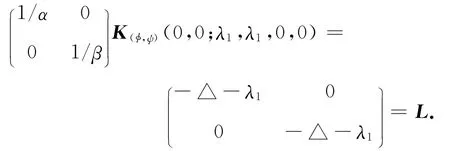

假设|a-λ1|、|c-λ1|、|α|、|β|<δ0,并令=α(φ1+)=β(φ1+).由投影P定义可知

显然,T(λ1,λ1,0,0)=0.类似地,有
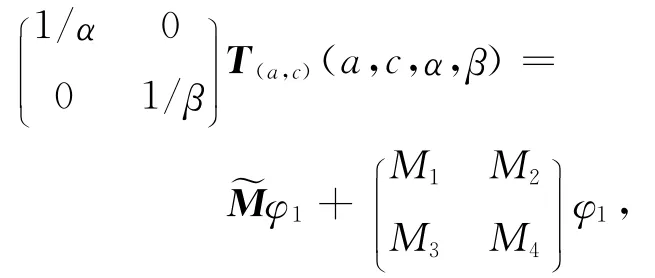

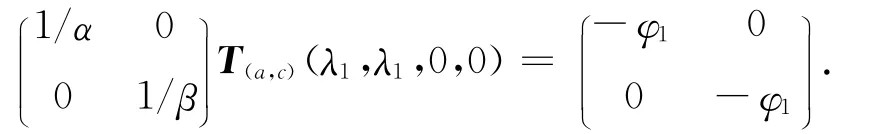
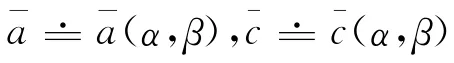
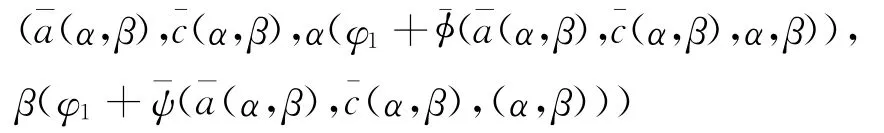
是系统(1)发自零解的分歧正解.
下面给出当α、β>0充分小时(α,β)(α,β)的线性近似表达式,将用在第2节判断上述正解的渐近稳定性.令
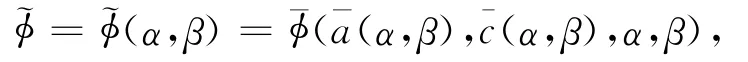

系统(1)发自零解的分歧正解可以表示为


将方程(7)的两边分别对α和β在(α,β)= (0,0)处求微分,得到

分别在(8)和(9)式的两边同时乘以φ1,然后在Ω上积分,由Green公式知

类似地,有
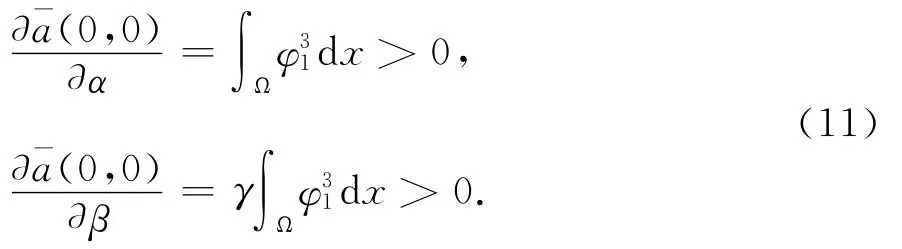
由(10)和(11)式可知,当α、β>0充分小时,

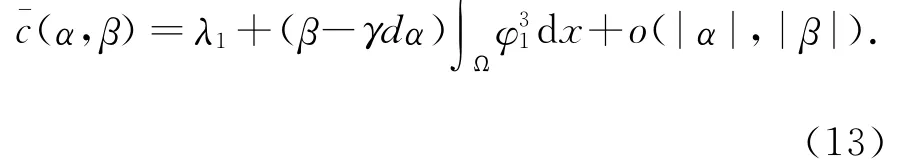
于是,得到本节的主要定理.
定理1 系统(1)存在发自零解的分歧正解,而且当α、β>0充分小时可以参数化为

其中(α,β)(α,β)的表达式见(12)和(13)式,而且(λ1,λ1,0,0)=0,(λ1,λ1,0,0)=0.
2 分歧正解的稳定性
通过线性化方法来判断前述正解的稳定性.假设α=β≐s.当s>0充分小时,发自零解的分歧正解(见定理1)可以由s参数化,即

系统(1)在((s),(s))处的线性化系统为


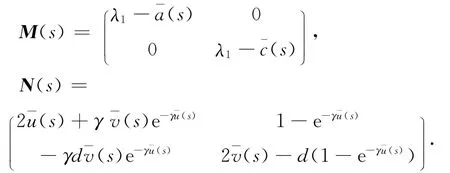
则系统(15)变形为B(s)U(L+M(s)+N(s))U=0,其中U= (u,v)T.系统(15)对应的特征值问题为

其中I是恒等算子.如果(16)式的所有特征值都位于右半复平面,那么(s),(s))渐近稳定;如果(16)式存在位于左半复平面的特征值,那么(s),(s))不稳定.
定理2 对于充分小的s>0,系统(1)的分歧正解((s),(s))渐近稳定.
证明 寻找特征值问题(16)的具有如下形式的特征函数(y,z):

其中m是复数,〈φ1,wi〉2=0,i=1,2.
令ξ= (φ1,0)T,η= (0,φ1)T,w= (w1,w2)T∈X2.于是,特征值问题(16)可以改写为


结合第1节中投影算子P、Q的定义,将Q作用于(18)式的两端,有

结合(19)和(21)式,定义算子E:X2×C×C×R→Y2×C:

显然,E(0,0;m,0)=0.现在给出E(w,μ)(w,μ;m,s)在(0,0;m,0)处的Frechét导数.通过计算,得到



由(12)和(13)式可知,

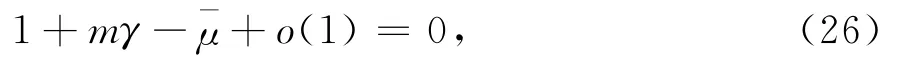
由(20)、(23)和(25)式可知

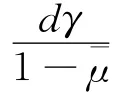
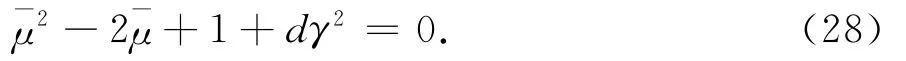
易知,方程(28)的所有根具有正实部,证毕.
3 数值模拟
这一节主要验证和补充上一节的理论分析结果.在一维空间区域模拟系统(1)对应的抛物系统.不失一般性,假设Ω= (0,2π),考虑系统

对系统(29)选择合适的参数,借助Matlab软件来模拟其解的情况(如图1—3所示).所有的图形均在充分大时刻做出,可以将它理解为平衡态解.这里,a=0.250 1.为描述不同的结果,其他参数c、d、γ>0待定.具体数值结果如下:
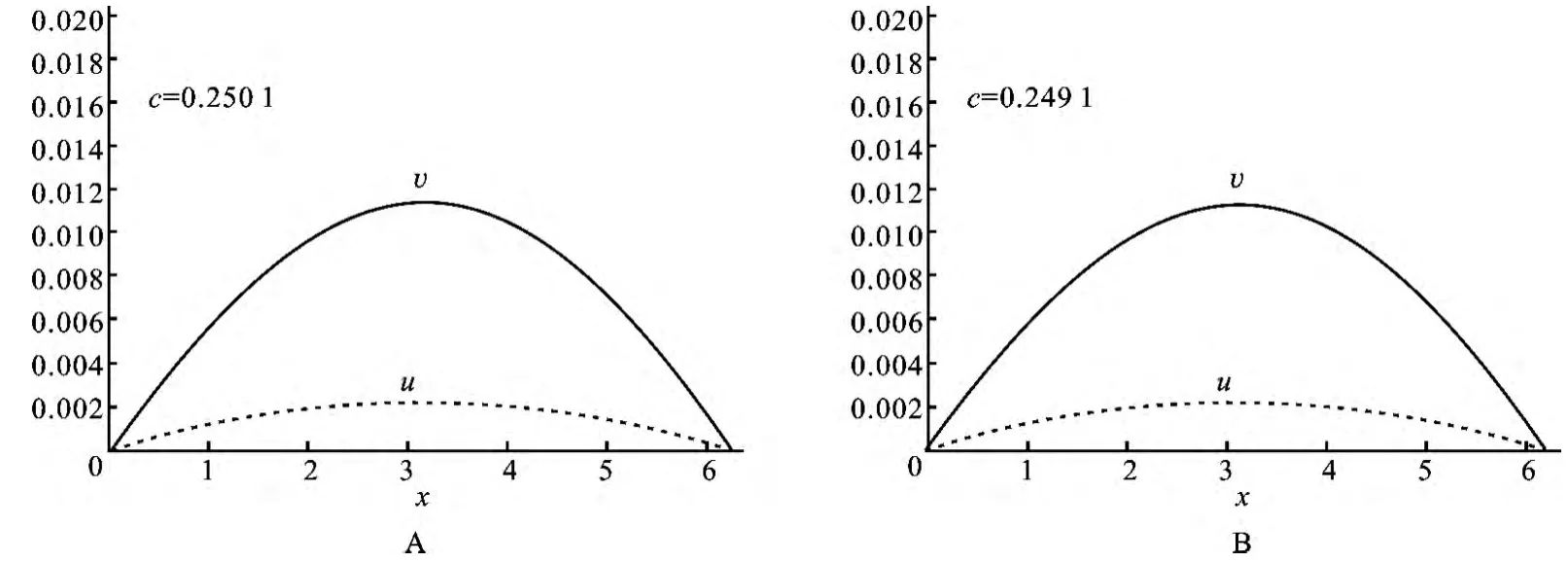
图1 系统(29)正平衡态解的存在性Fig.1 Existence of positive steady-state solution to system (29)
(1)已知a(c)表示食饵(捕食者)的自然增长率.假设a>λ1,c+d>λ1,如果|a-λ1|、|c-λ1|充分小,那么系统(29)存在正平衡态解.这与本文的分析结果一致.
(2)参数γ对系统(29)的正平衡态解存在性的影响(γ表示捕食者捕杀食饵的效率).存在常数γ1、γ2>0使得,当γ<γ1时系统(29)存在正平衡态解,当γ>γ2时系统(29)没有正平衡态解.进一步,当γ→0+时,系统(29)存在正平衡态解,而且趋向(θa,θc).

图2 参数γ对系统(29)的正平衡态解存在性的影响Fig.2 Effect ofγon the existence of positive steady-state solution to the system (29)
(3)参数d对系统(29)的正平衡态解存在性的影响(d表示食饵转化为捕食者的转化率).存在常数d1、d2>0使得,当d<d1时系统(29)存在正平衡态解,当d>d2时系统(29)没有正平衡态解.这与捕食-食饵模型的生物意义是一致的.
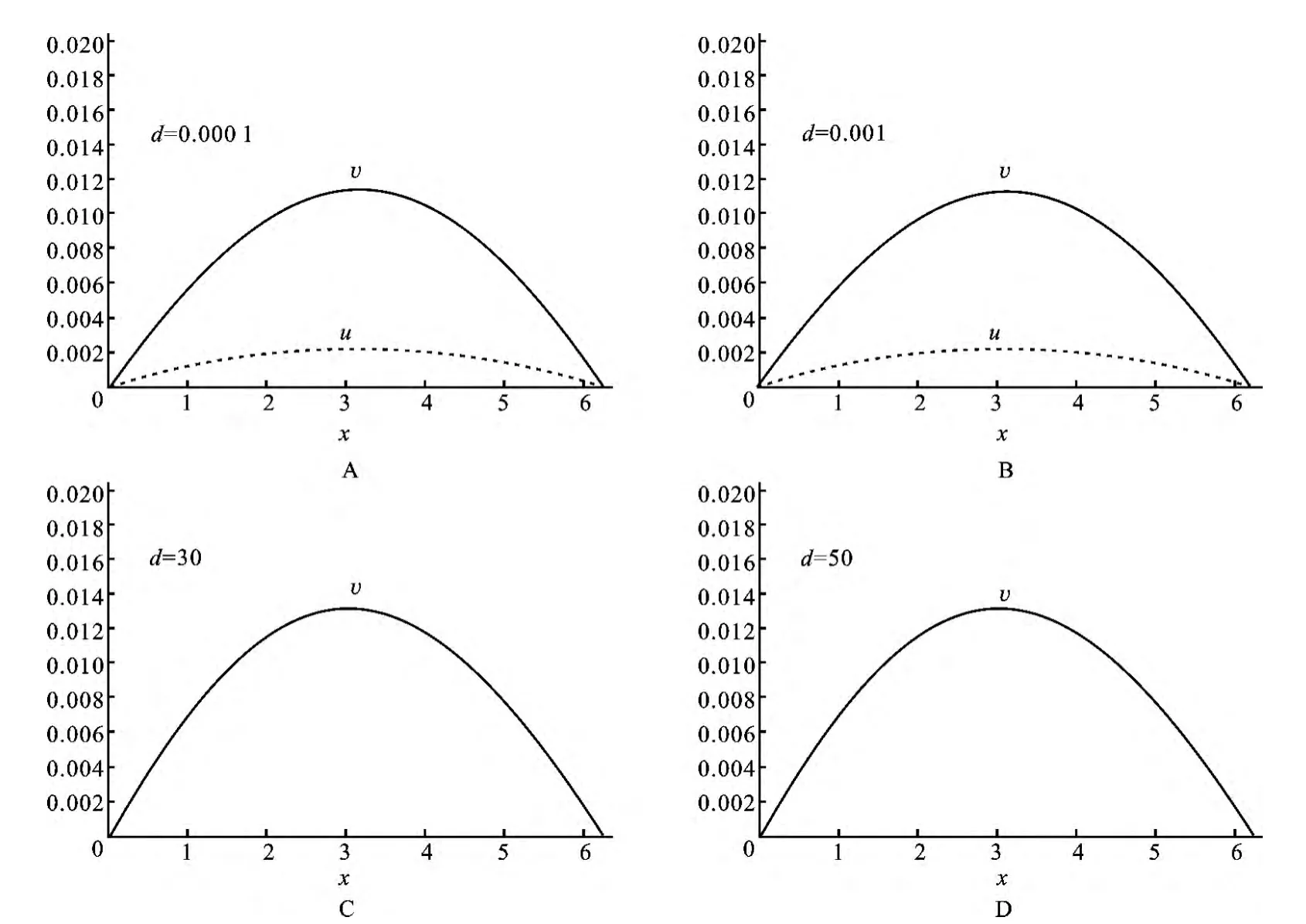
图3 参数d对系统(29)的正平衡态解存在性的影响Fig.3 Effect of don the existence of positive steady-state solution to the system (29)
[1]Ivlev V.Experimental ecology of the feeding fishes[M].New Haven:Yale University Press,1961.
[2]Rosenzweig M L.Paradox of enrichment:Destabilization of exploitation ecosystems in ecological time[J].Science,1971,171:385-387.
[3]May R.Limit cycles in predator prey communities[J].Science,1972,177:900-902.
[4]Kooij R E,Zegeling A.A predator-prey model with Ivlev′s functional response[J].Journal of Mathematical A-nalysis and Applications,1996,198(2):473-489.
[5]Sugie J.Two-parameter bifurcation in a predator-prey system of Ivlev type[J].Journal of Mathematical Analysis and Applications,1998,217(2):349-371.
[6]Liu Bing,Zhi Ying,Chen Lansun.The dynamics of a predator-prey model with Ivlev′s functional response concerning integrated pest management[J].Acta Mathematicae Applicatae Sinica:English Series,2004,20(1):133-146.
[7]Xiang Zhongyi,Song Xinyu.The dynamical behaviors of a food chain model with impulsive effect and Ivlev functional response[J].Chaos Solitons Fractals,2009,39(5):2282-2293.
[8]Ling Li,Wang Weiming.Dynamics of a Ivlev-type predator-prey system with constant rate harvesting[J].Chaos Solitons Fractals,2009,41(4):2139-2153.
[9]Rao Feng,Wang Weiming,Li Zhenqing.Spatiotemporal complexity of a predator-prey system with the effect of noise and external forcing[J].Chaos Solitons Frac-tals,2009,41(4):1634-1644.
[10]Jia Yunfeng.A sufficient and necessary condition for the existence of positive solutions for a prey-predator system with Ivlev-type functional response[J].Applied Mathematics Letters,2011,24(7):1084-1088.
[11]Guo Gaihui,Li Bingfang,Lin Xiaolin.Qualitative analysis on a predator-prey model with Ivlev functional response[J].Advances in Difference Equations,2013,2013(1):164-177.
[12]Delgado M,López-Gómez J,Suárez A.On the symbiotic Lotka-Volterra model with diffusion and transport effects[J].Journal of Differential Equations,2000,160(1):175-262.
[13]Yamada Y.Stability of steady states for prey-predator diffusion equations with homogeneous Dirichlet conditions[J].SIAM Journal on Mathematical Analysis,1990,21(2):327-345.
[14]Kielhofer H.Bifurcation theory:An introduction with applications to PDEs[M].New York:Spring-Verlag,2004:7-11.
[15]Ma Tian,Wang Shouhong.Bifurcation theory and applications[M].Singapore:World Scientific,2005:1-2.
[16]Smoller J.Shock waves and reaction-diffusion equations[M].New York-Berlin:Springer-Verlag,1983:168-171.
[17]Gilbarg D,Trudinger N S.Elliptic partial differential equations of second order[M].Berlin:Springer-Verlag,2001:446-450.

