临近空间无动力攻击器修正弹道建模与仿真
何 苹,王莹莹,贺 波,张圣杰
(空军工程大学,陕西 西安 710051)
0 引言
利用高动态临近空间平台的的高度、速度优势,从临近空间平台发射无动力攻击器,从顶部攻击敌方高价值目标是一种有前景的作战方式[1]。弹道建模是攻击器作战性能研究的基础。传统弹道建模中,因导弹射程不远,弹道高度较低,经常对影响弹道的某些因素作一些假设,如直接应用地面测得的空气动力系数曲线,用插值法确定气动力系数;将地球视作平面,忽略地球曲率的影响,不考虑地球椭球体造成的影响;忽略地球自转的影响等[2]。在常规导弹弹道研究中,这些因素的影响较小,简化假设是合理的。对远程导弹弹道建模的研究,为临近空间无动力攻击器弹道建模提供了参考。文献[3]用近似法对全球到达高超声速飞行器的弹道特性进行了分析;文献[4]针对远程弹箭飞行空域、速度的跨度和变化大的特点,对远程弹箭弹道特性进行了研究。本文综合考虑高空气动力、重力加速度随高度与纬度的变化,地球自转,以及地表曲率等因素对临近空间无动力攻击器弹道的影响,并用仿真计算分析上述因素的影响程度。
1 临近空间无动力攻击器弹道影响因素
1.1 空气动力模型
计算作用在攻击器上的空气动力,关键是确定空气动力系数。攻击器小攻角、小侧滑角飞行时,可近似认为

式中:CD,CL,CZ分别为阻力、升力和侧力系数;α,β分别为攻角和侧滑角为升力系数梯度;为侧力系数梯度;为拟合系数;CD0为零升阻力系数,是飞行马赫数Ma与飞行高度h的函数[4-6]。研究发现:攻击器超声速飞行时,CD0随Ma变化趋势符合Logistic下降型曲线的特点,随h变化趋势符合Logistic上升型曲线的特点,因此用Logistic曲线拟合CD0[7]。
高度相同时(h=0km),分别用文献[6]中的拟合公式和Logistic曲线拟合CD0的相对误差见表1。Ma为3时,分别用文献[6]中的拟合公式和Logistic曲线拟合CD0的相对误差见表2,表中原始数据由文献[4]中数据插值获得。
由表1、2可知:与文献[6]的拟合公式相比,Logistic曲线对临近空间攻击器CD0的拟合精度更高。因此,本文临近空间无动力攻击器弹道建模中,CD0采用Logistic拟合公式
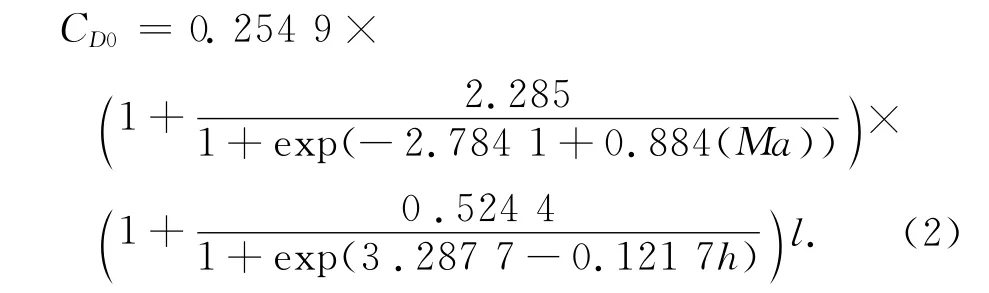
式中:l为弹形系数。
1.2 重力加速度计算模型
地球实际是一椭球体,重力加速度可表示为

式中:φs为地心纬度;a为椭球体长半轴长度;J为地球一阶扁率系数,且J=1.5J2;f为引力常数;M为地球质量;q为赤道上一点的离心惯性力与重力之比值,且q=ω2a3/(fM);r为攻击器质心至地心的距离,且r=R+h。此处:J2为地球形状动力学系数;ω为地球自转角速度;R为地面点到地心的距离,且
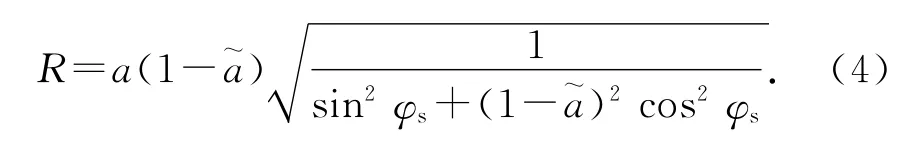
其中:为椭球体扁率。
对式(3),J=0时,可得将地球视为圆球体时重力加速度gpel的表达式为

式中:为地球平均半径;r=+h。
椭球体地理纬度Bell,φs与μ的关系可表示为
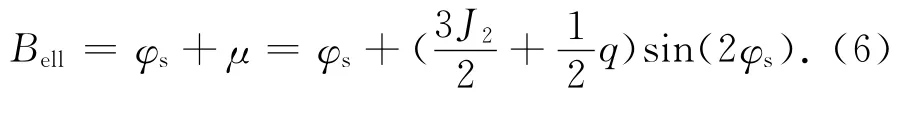
式中:μ为地球重力线与地心矢径间的夹角。
对式(6),J2=0时,可得圆球体的地理纬度Bpel,φs的关系可表示为

由式(3)、(5)、(6)、(7),采用牛顿迭代法,可计算临近空间攻击器处于不同高度(0~60km)、不同地理纬度(10°~60°),考虑与不考虑地球扁率时重力加速度的差异。经计算,在高度60km、北纬30°时,地球扁率对重力加速度的影响最大,但差值仅0.121 96%。因此,在临近空间无动力攻击器弹道建模中,忽略地球扁率的影响,将地球视为圆球体。则g的表达式为

表1 相同高度零升阻力系数拟合Tab.1 Coefficients of zero-lift drag on the same height

表2 相同马赫数零升阻力系数拟合Tab.2 Coefficients of zero-lift drag wit the same Math number
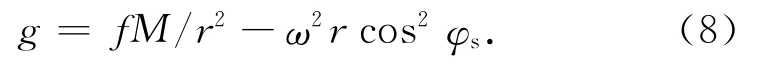
1.3 考虑地球曲率及自转影响
将地球视为旋转的圆球体,考虑离心惯性力、柯氏惯性力和牵连惯性力对攻击器弹道的影响[8]。假设攻击器在赤道平面内水平飞行,此时攻击器弹道倾角θ=0°,φs=0°,则

式中:m为攻击器质量;vm为攻击器速度;D为空气阻力;L为空气升力。
可见,离心惯性力的影响表现为m(vm)2/r,与vm平方成正比,与距离r成反比;柯氏惯性力的影响表现为2mvmω,与vm成正比,与r无关;牵连惯性力的影响表现为mω2r,与r成正比,与vm无关。
设攻击器飞行高度分别为7,30,60km,在每一高度飞行速度分别为200,1 000,1 500,2 000m/s,计算离心惯性力、柯氏惯性力、牵连惯性力与重力之比,结果见表3。由表3可知:随着攻击器飞行高度增大,三项附加力对攻击器弹道的影响略增,但不明显;从三项附加力的影响程度看,离心惯性力的影响最大,柯氏惯性力的影响次之,牵连惯性力的影响最小。其中牵连惯性力对攻击器弹道的影响最大值仅0.356%。因此,在临近空间无动力攻击器弹道建模中,考虑离心惯性力、柯氏惯性力攻击器弹道的影响,忽略牵连惯性力的影响。

表3 三部分附加力对攻击器弹道的影响Tab.3 Analysis of the influence of additional force on pursuer trajectory
2 临近空间无动力攻击器修正弹道建模
在常规弹道模型的基础上,综合考虑高空空气动力、重力加速度随高度与纬度的变化、地球曲率及自转等因素的影响,可得临近空间无动力攻击器质心在发射坐标系中的动力学方程组
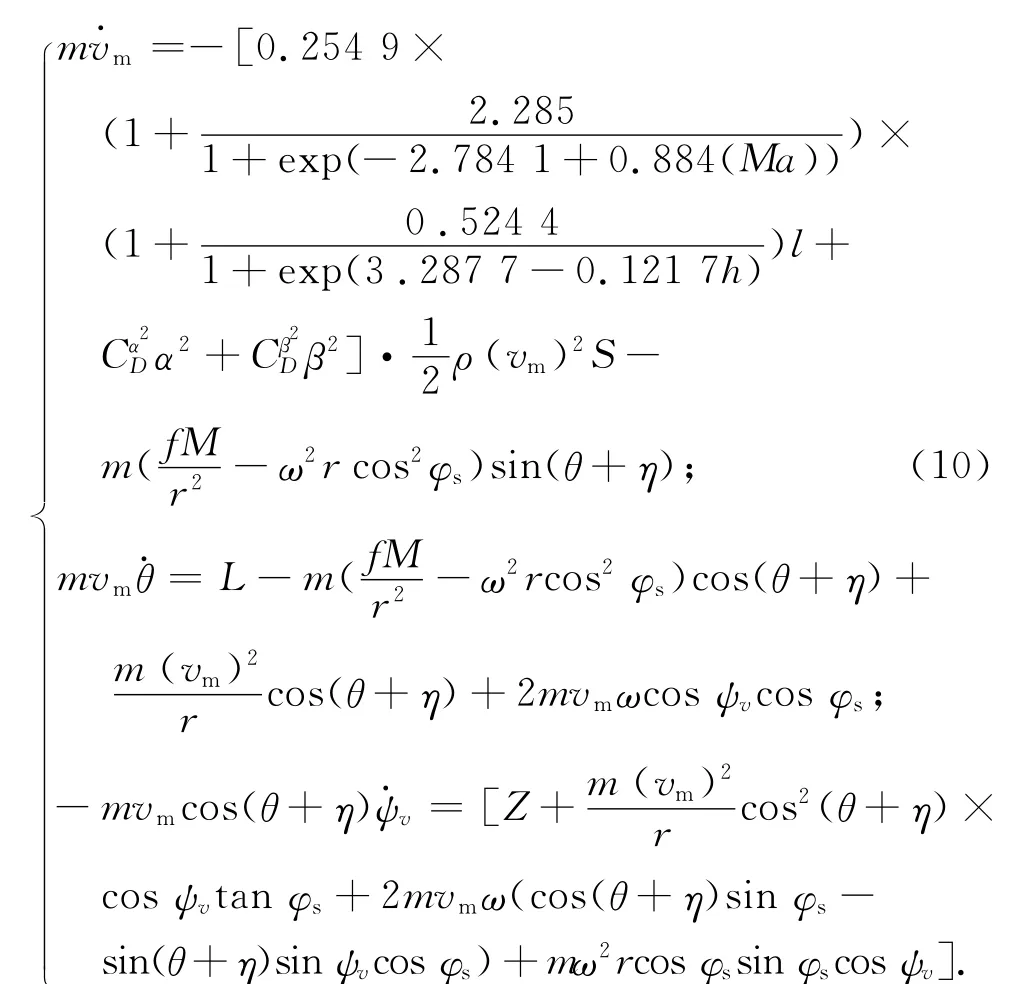
式中:ρ为空气密度;θ为攻击器弹道倾角;η为极坐标角;ψv为弹道偏角;L为空气升力;Z为空气侧力。本文只给出考虑以上因素的变化部分,常规弹道的动力学模型参考文献[2]。
3 仿真结果与分析
为校验本文建立的临近空间无动力攻击器弹道模型的合理性,并分析高空空气动力、重力加速度随高度与纬度的变化、地球曲率及自转等因素对攻击器弹道的影响,分别对综合考虑与不考虑上述因素的弹道模型进行仿真。仿真条件为:临近空间平台高度42km,以速度1 800m/s、发射角0°发射无动力攻击器,攻击距离150km外、高度10km,以Ma=0.7、半径50km作圆周巡航的目标,采用比例导引弹道,比例系数为4。三自由度弹道如图1所示。
由图1可知:两种弹道有较大差异。在相同发射条件下,攻击器采用常规弹道模型时,攻击器、目标遭遇点的坐标为(149 100,10 010,22 740)m,采用本文的修正弹道模型,攻击器、目标遭遇点的坐标为(149 200,8 253,19 820)m。两种弹道模型仿真中飞行性能见表4。由表4可知:末速度相差9.4%,平均速度相差2.0%,作战飞行时间相差1.9%,对临近空间无动力攻击器来说,此差别不容忽视。因此,对临近空间攻击器弹道建模,有必要综合考虑高空空气动力、重力加速度随高度与纬度的变化、地球曲率及自转等因素的影响。

图1 三自由度理想弹道Fig.1 Three-axis normal trajectory
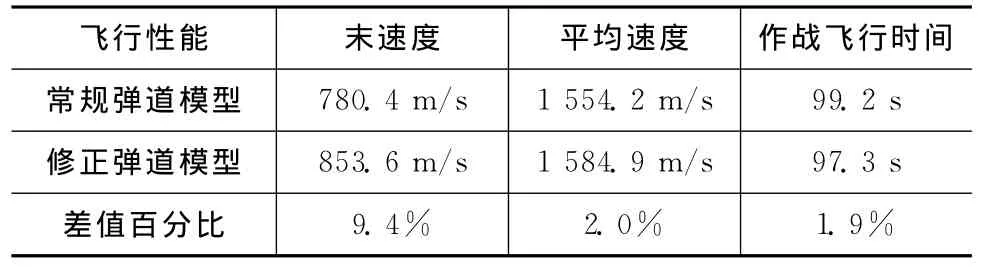
表4 两种弹道模型对应攻击器飞行性能指标Tab.4 Flight performance index result of trajectory models
4 结束语
针对临近空间无动力攻击器的特殊飞行情况,基于尽可能减小误差的原则,本文对弹道模型的精确化进行了研究。定量分析了高空空气动力、重力加速度随高度与纬度的变化、地球曲率及自转等因素对攻击器弹道的影响,并建立了适于临近空间无动力攻击器的修正弹道模型。仿真结果表明,综合考虑上述因素是必要的。研究结果对临近空间攻击器总体方案设计有一定的参考价值。
[1] HE Ping,YANG Jian-jun.Feasibility analysis of near space un-powered guided bomb when attacking aerial target based on genetic algorithm[C]//ICIECS 2009.Wuhan:ICIEC,2009:1516-1519.
[2] 雷虎民.导弹制导与控制原理[M].北京:国防工业出版社,2006.
[3] PERSTON H C,DARRY J P.Approximate performance of periodic hypersonic cruise trajectories for global reach[C]//Proceedings of AIAA 8thInternational Space Planes and Hypersonics and Technologies Conference.Norfolk:AIAA,1998:1-6.
[4] 李臣明.高空气象与气动力对远程弹箭弹道影响的研究[D].南京:南京理工大学,2007.
[5] 孙 鹏,张合新,孟 飞.再入飞行器最优减速研究[J].导弹与航天运载技术,2006(2):1-5.
[6] 张 毅,肖龙旭,王顺宏.弹道导弹弹道学[M].长沙:国防科技大学出版社,2005.
[7] 何 苹,杨建军.临近空间导弹空气阻力系数的Logistic曲线拟合[A]:军事系统工程年会论文集[M].北京:海潮出版社,2009:626-629.
[8] 张 弫.远程反空气动力目标拦截器推进和弹道问题优化研究[D].北京:中国航天科工二院,2002.

