变轨条件下卫星贮箱内液体推进剂晃动特性三维数值模拟
张博譞,李国岫,虞育松
(北京交通大学 机电学院,北京 100044)
0 引言
在微重力或零重力环境中,充液航天器内液体晃动及其对控制系统的影响是当前国内外航天技术研究的重要课题。微重力条件下的液体流动行为研究始于20世纪60年代,研究对象是火箭推进剂罐内的液体晃动动力学特性。随后,低重力条件下的在轨空间飞行器燃料贮箱内的液体晃动特性被重点研究。随着航天事业的发展,推进剂占火箭、卫星等航天器总质量的比重不断加大,推进剂晃动与箭体姿态运动通过惯性力的相互作用力而直接耦合。晃动不稳定,晃动幅值不断增大,火箭姿态角就会因晃动不断加大,从而导致箭体姿态运动发散[1]。充液航天器总体设计中必须考虑液体晃动,推进剂的运动对在轨航天器的稳定、定位、对接的影响相当关键[2]。在星体充液量不断增大和控制飞行器姿态的指向精度条件下,并考虑零重力或微重力环境,充液体晃动动力学的研究显得更重要和复杂[3]。
在液体的晃动对航天器的稳定性研究中,为便于分析,大量研究采用了等效单摆模型和质量-弹簧力学模型[4]。分析中进行了简化,忽略了部分力的影响,故与微重力或零重力下的实际状态相比,仍有一定差异。对微重力或零重力下的液体晃动的研究多为定体积,而航天器在变轨过程中必然使用液体推进剂,使贮箱内液体推进剂体积减小,且微重力或零重力下的液体晃动是一个非线性问题,这导致变轨过程中的液体晃动问题的研究更复杂。工程中最关心晃动频率和阻尼两个参数。在充液卫星姿态控制中,计算晃动频率以在设计中避免壁面液体晃动、姿态运动和弹性附件振动的共振,晃动过程中的阻尼与章动发散时间直接相关。在卫星入轨后,姿态控制系统必须在一定时间内及时开启,防止卫星章动发散失稳[5]。采用三维数值模拟对液体流动过程进行直接模拟,不作简化假设,对液体晃动的阻尼比和频率的预测更准确,同时能得到更直观的流场、压力、速度分布图,便于对流体流动过程做更进一步的研究。
本文用Fluent三维数值模拟软件,以某卫星液体推进剂贮箱为研究对象,在零重力环境中,选取不同充液比,对卫星变轨过程液体的分布及重定位进行预测。
1 基本方程
不相容气液两相牛顿流体的可压缩N-S方程为
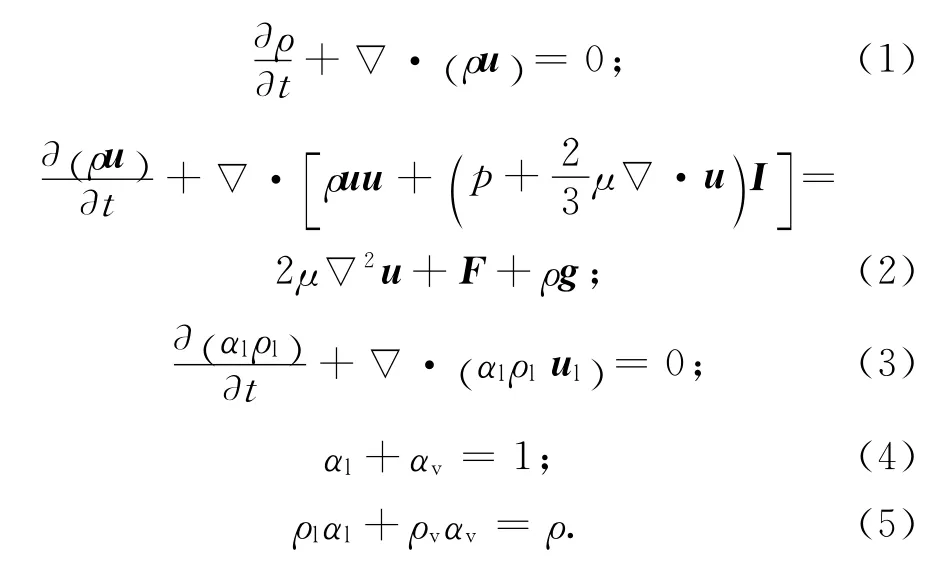
式中:ρ为流体密度;p为流体微元上的压力;I为单位对称矩阵;αl,αv分别为两相的体积分数;ρl,ρv分别为两相的密度;u为速度;F为表面张力;g为重力。
瞬态、不可压、不相溶、等温、定黏度且存在表面张力(不相溶)的两相牛顿流体Navier-Stokes方程为
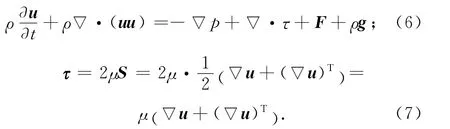
式中:τ为流体的黏性应力;S为应变率张量。式(6)、(7)考虑了压力、湍流、表面张力和重力对流动的影响。由于气液两相不相溶,相与相间存在一个界面,故相界面上存在法向的F。F与液体性质,液面曲率相关,有
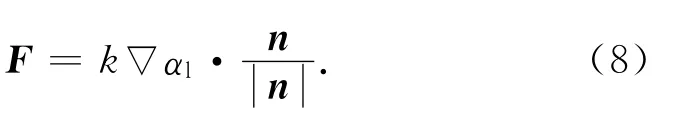
式中:n为法向向量。
为建立准确的近壁面数学模型,引入重整化群(RNG)k-ε双方程湍流模型。
标准k-ε模型中湍动能k和耗散率ε可表示为

式中:Gk为由平均速度梯度引起的湍动能;Gb为用于浮力影响引起的湍动能;YM为可压速湍流脉动膨胀对总的耗散率的影响;C1ε,C2ε,C3ε为经验常数,且C1ε=1.41~1.45,C2ε=1.90~1.92,C3ε=0.8。
标准k-ε模型也有一定的局限性,主要表现在:采用了Boussinesq假定,即采用了雷诺应力与平均速度梯度线性关联的梯度型和湍流黏性系数各向同性的概念,使k-ε模型难以准确模拟剪切层中平均场流动方向的改变对湍流场的影响。
重整化群k-ε模型是对瞬时的 Navier-Stokes方程用重整化群的数学方法推导而得。模型中的常数与标准k-ε模型不同,且方程中也出现了新的函数或项。其湍动能及耗散率方程的形式与标准k-ε模型相似。重整化群k-ε模型有助于处理低雷诺数和近壁流动问题的模拟。RNGk-ε模型的可信度和精度较标准k-ε模型更高。因此,本文的数值模拟研究采用RNGk-ε模型。
不相容的气液两相,相与相间存在界面。不同流体分子间作用力的差异将导致相界面上出现张力。利用体积分数(VOF)模型能只用一组N-S方程就可描述气液两相及相界面,使问题得以简化。位于相界面处的单元内气液两相同时共存,非相界面单元只存在单相。因此,引入k相的体积分数εk,某个单元内εk可表示为
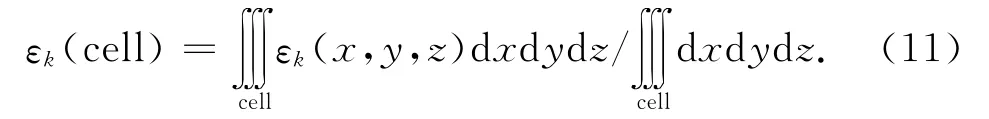
整个流场单元可被分为3个区域:εk(cell)=0时,单元内不存在k相流体;εk(cell)=1时,单元内只存在k相流体;0<εk(cell)<1时,单元内有相界面存在。
在微重力或零重力环境中,毛细力作用占主导地位,液体表面高度弯曲,且贮箱结构对液体定位的影响非常大。当邦德数Bo≤1时,毛细力占主导地位。Bo为惯性力与毛细力的比值,有
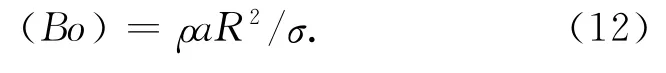
式中:σ为液体表面张力;a为加速度;R为贮箱特征尺寸[5]。文献[7]给出了圆柱容器内液体小幅晃动第一阶模态阻尼比的经验公式
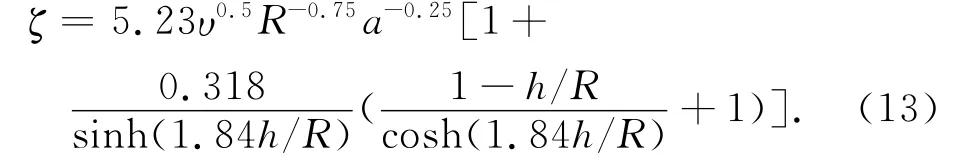
式中:υ为液体运动黏性系数;R为容器半径;h为容器内的液深。当h/R>1时,阻尼比基本不随液深变化。
2 计算结果及分析
推进剂甲基肼(MMH)的密度为875kg/m3(20℃),黏性系数为0.000 855Pa·s,表面张力系数为0.034N/m。某卫星推进剂贮箱结构如图1所示。考虑模型为对称结构,为节省计算时间,减小计算区域,将模型纵剖,推进剂贮箱的一半作为计算区域。将剖面设置为对称面。对卫星某次变轨过程行数值模拟,变轨过程初始条件为:变轨过程加速度3.78×10-3m/s2;微重力方向为-Z向;充液比0.89;变轨过程中的液体流出流量34.066g/s。
用Fluent三维数值模拟软件,对零重力环境中贮箱内液体推进剂分布及重定位过程进行了数值模拟。在零重力条件下,对贮箱有液体推进剂流出时的变轨过程进行了数值模拟计算。
变轨工况下液体质心变化的计算结果如图2所示。由图可知:整个流动过程的时间约4 000s;变轨过程初期(0~1 000s),贮箱内液体发生较大振幅的阻尼振荡,液体晃动幅值逐渐减小,同时液体质心位置随出箱内液体量的减少(液体的Z向质心位置线性下降)。变轨过程后期(1 000~4 000s),液体晃动幅度逐渐趋近于零,液体质心由于液体量减少而呈线性下降。
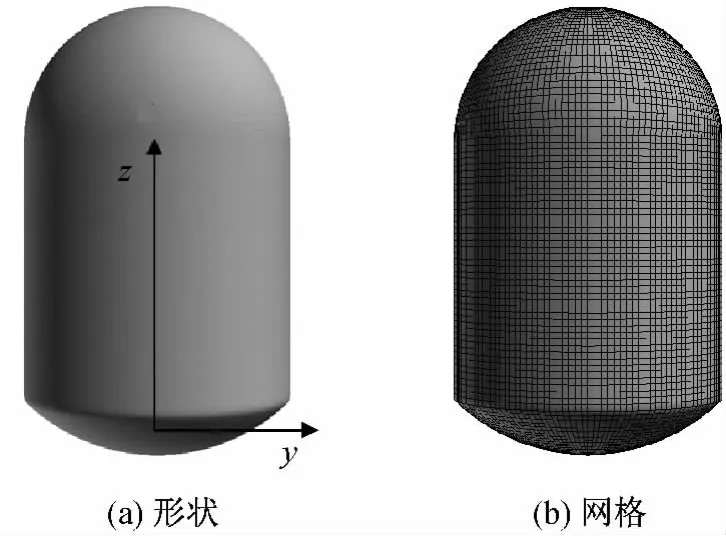
图1 贮箱结构Fig.1 Structure of tank
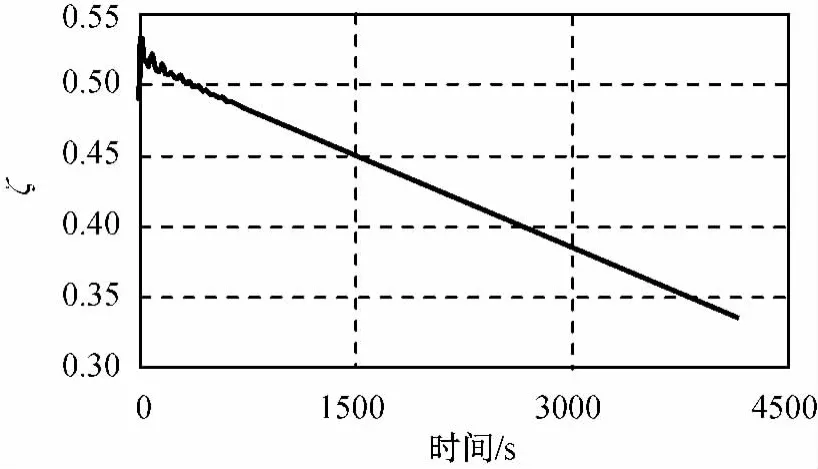
图2 变轨工况下液体质心(Z向)变化Fig.2 Change of gravity center of liquid(Zdirection)
变轨过程中,时刻t=0,136,1 336,4 180s和变轨结束后液面稳定状态下的轴线截面以及三维液面透视图如图3所示。
由于气液固界面处存在毛细力作用,在气液固界面处液面会与固体壁面呈一定角度,称为接触角。接触角是在固、液、气三相接触达到平衡时,三相接触周边的任一点上,液气界面切线与固体表面间形成的并包含液体的夹角。该值与固体、液体和气体属性均有关系。不同情况下,接触角可为0°~180°。文献[8]用光学张量测量法得到MMH与铝制容器间的接触角在10°附近。本文将MMH与铝制容器间的接触角定在10°[8]。
因存在接触角,微重力或零重力下贮箱内液体推进剂的液面不会为水平液面,液面会在毛细力与表面张力的共同作用下沿壁面爬升,直至固液气三相接触达到平衡。上述算例中的变轨零时刻液面为数值模拟形成,即将初始液面设置为水平液面,使液面在完全失重条件下沿壁面自由爬升,达到稳定平衡状态(质心稳定不再变化,且液面基本停止波动),并将此时刻作为变轨过程的初始时刻(图3(a))。
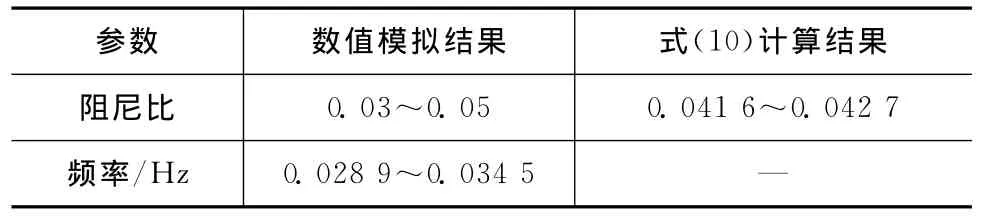
表1 两次变轨过程的液体晃动阻尼比和频率Tab.1 Damping ratio and frequency of liquid sloshing during two orbit changes
变轨过程中贮箱内液体不断流出,导致液面持续下降(贮箱内液深持续变化),且加上变轨初期液面有较大幅度晃动,故数值模拟方法与式(13)求得的阻尼比均为变动值。
不同液深时刻阻尼比的数值模拟计算值与经验公式的计算值如图4所示。由图可知:本文的计算结果与经验公式计算结果非常接近。国内学者曾对液体晃动的阻尼比进行简化计算,利用速度势函数推导的计算液体晃动频率和阻尼的特征值方程,简化处理转化为一般的广义特征值。其结果为充液比为0.5时,ζ为5.67×10-4[5]。此结果与由阻尼比经验公式得出的值相差非常大,故可认为简化计算对阻尼的预测结果并不可靠。本文模拟能较准确地得出的变轨过程中液体晃动的阻尼比。
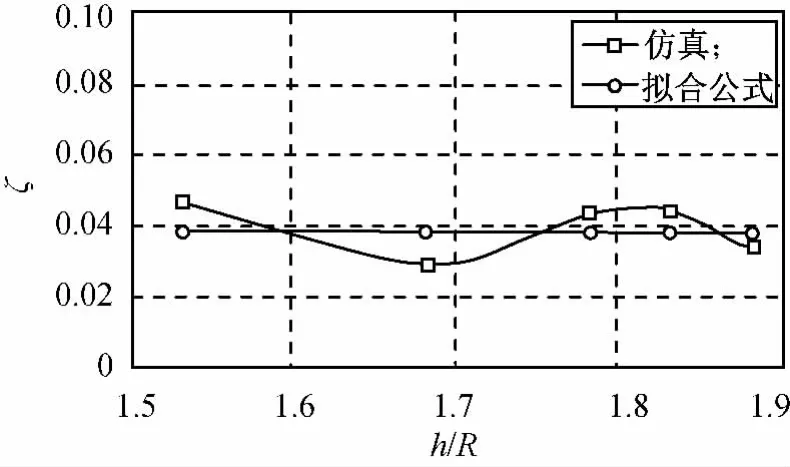
图4 不同液面高度晃动阻尼比计算结果对比Fig.4 Calculation results of damping ratios with various liquid height ratios
变轨过程初始时刻贮箱内流线如图5所示。由图可知:贮箱内液体推进剂甲基肼与氦气的流动趋势,甲基肼为Z轴负向流动。这一方面是贮箱模型底部有甲基肼质量流量出口,另一方面是变轨过程加速度为Z轴负向,导致液体推进剂会在变轨过程中有下沉的趋势。
变轨过程时刻136s贮箱内流线和速度场分别如图6、7所示。由图6、7可更直观地观察在变轨过程中贮箱内甲基肼与氦气的流动状态,甲基肼在贮箱近壁面处与贮箱中部的速度方向相反,即贮箱内甲基肼已开始在Z轴方向呈现震荡。

图5 变轨初期贮箱内流线Fig.5 Path line of flow in tank at begin of orbital transfer
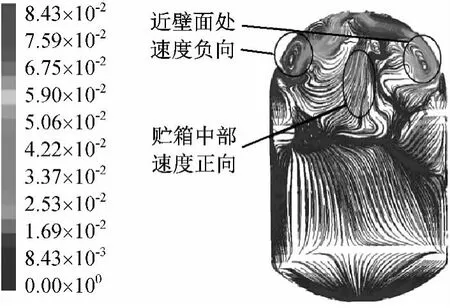
图6 变轨时刻136s贮箱内流线Fig.6 Path line of flow in tank at 136sof orbital transfer
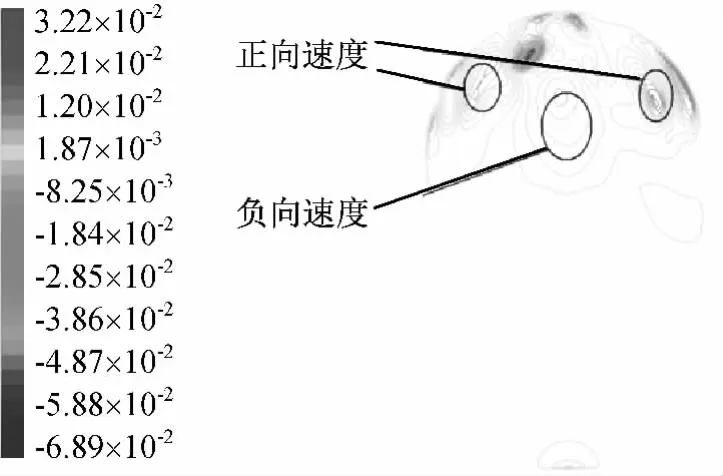
图7 变轨时刻136s贮箱内速度场Fig.7 Velocity field in tank at 136sof orbital transfer
甲基肼对贮箱的作用力如图8所示。由图可知:变轨开始后贮箱受到的作用力迅速增至约1.6N,作用力为Z轴负向;随后作用力出现衰减振荡;贮箱受到的作用力在变轨初期振荡衰减,随着变轨过程的进行以及贮箱内甲基肼体积的减少,作用力大小呈线性降低。

图8 变轨贮箱Z向受力变化过程Fig.8 Change of force of tank inZdirection during orbit change
贮箱内甲基肼在变轨前后质心的变化如图9所示。一方面,变轨过程中甲基肼以恒定的质量流量流出贮箱,导致变轨后甲基肼的体积较变轨前不断减少,另一方面,考虑表面张力的作用,液体在晃动中会有发散趋势,即随着时间的增加,自由液面不再回到其初始静平衡位置[3]。
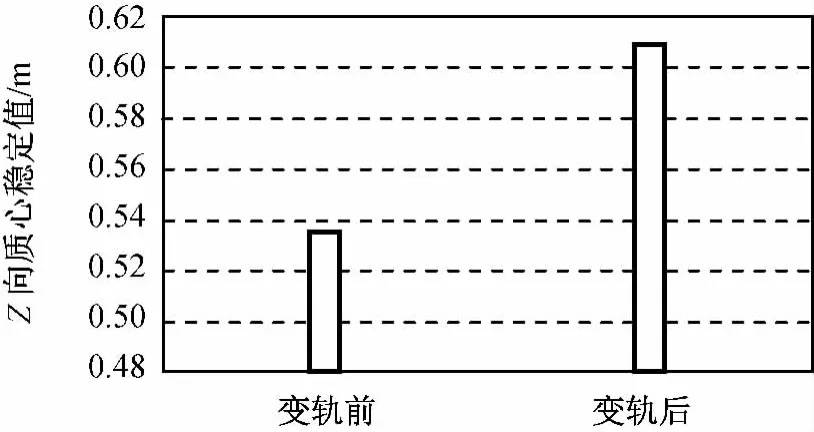
图9Z向质心稳定值Fig.9 Stable value of gravity center inZdirection
3 结束语
本文以某卫星作为研究对象,对变轨条件下贮箱内液体推进剂晃动特性进行了三维数值模拟。获得了卫星变轨过程中,液体推进剂的质心变化、液体推进剂对贮箱作用力变化、液体推进机晃动一阶频率以及液体推进剂的一阶晃动阻尼比,通过贮箱内的流场分布图和速度场图,直观地给出变轨过程中贮箱内推进剂的流动过程及流动的变化趋势。由本文数值模拟结果可知,考虑表面张力时液体晃动具有发散的趋势,即随着时间的增加,自由液面不再回到其初始静平衡位置,与文献[3]中的结论吻合。随时间的增加,贮箱壁面处的液体平衡位置有所增加,这说明将有更多液体依附壁面,从而引起液体晃动质量的降低。将本文得出的阻尼比数值模拟计算值与由实验值拟合出的经验公式得出的阻尼比计算值进行对比。可发现两者非常接近,即在对卫星变轨过程中,卫星贮箱内液体推进剂的阻尼比预测准确度较高。
[1] 尹立中,王本利,邹经湘.航天器液体晃动与液固耦合动力学研究概述[J].哈尔滨工业大学学报,1999,31(2):118-122.
[2] 陈存芸.运载火箭三级无动力飞行段晃动稳定性研究[J].上海航天,2004,21(4):29-33.
[3] 岳宝增,刘延柱.低重力环境下三维液体非线性晃动的数值模拟[J].宇航学报,2000,21(4):25-30.
[4] 包光伟,刘延柱.三轴定向充液卫星的姿态稳定性[J].空间科学学报,1993,13(1):31-38.
[5] 李俊峰,鲁 异,宝音贺西,等.贮箱内液体小幅晃动的频率和阻尼计算[J].工程力学,2005,22(6):87-90.
[6] 王 毅,常小庆.微重力环境下推进剂贮箱中三维气液平衡界面的数值模拟[J].火箭推进,2007,33(3):31-35.
[7] ABRAMSON H N.The dynamic behavior of liquids in moving containers[R].NASA SP 106,1966.
[8] 王 为,李俊峰,王天舒.航天器贮箱内液体晃动阻尼研究(二):数值计算[J].宇航学报,2006,27(2):177-180.
[9] KREPPEL S.Scaling and modeling of propellant sloshing and zero gravity equilibrium for the orion service module propellant tanks[D].Kenosha:Carthage College,2010.

