动静隔离、主从协同控制双超卫星平台设计

张 伟，赵艳彬，廖 鹤，赵洪波

（上海卫星工程研究所，上海 200240）

0 引言

随着高分辨率对地观测、大比例尺立体测绘、激光通信、深空观测等未来先进航天器搭载的有效载荷越来越精密，对卫星平台提出了超高指向精度、超高稳定度（双超）的需求［1－5］。如未来1∶5 000比例尺测绘卫星指向精度需求达到5×10－4（°）量级，姿态稳定度需求达到5×10－6（°）／s量级。但采用当前的卫星平台设计方法，指向精度仅为10－3（°）量级，姿态稳定度10－4（°）／s量级，已无法满足需求。因此，先进航天器的“超精超稳”控制已成为卫星平台有待突破的瓶颈。制约卫星平台超精超稳的主要因素是活动部件和挠性部件引发的平台干扰［6］。活动部件如飞轮、制冷机、推力器等工作时产生的各频段随机扰动和振动，极大地影响了卫星平台指向精度和姿态稳定度，是引起载荷振动的主要原因。太阳帆板、大型展开天线等挠性部件不仅引发卫星平台的干扰，而且其低频模态也极大地限制了控制系统带宽，导致控制系统性能不能发挥。目前，针对卫星平台干扰，主要采用抑制与隔离两种方法。本文对一种振源与载荷动静空间隔离、控制主从协同”的双超卫星平台设计进行了研究。

1 基于隔振器的平台干扰抑制方法

目前，抑制卫星挠性附件抖动和活动部件振动的主要手段有被动隔振、主动隔振及主被动隔振方法。

1.1 被动隔振

被动隔振是指在振源与系统间加入弹力刚性单元、能量耗散单元（吸收振动）或能量阻尼单元（负载振动路径）所构成的子系统。

被动隔振装置是一紧凑的连接器，结构简单，实现易，经济性好，可靠性高，且无需外部能量和信息，对卫星平台活动和挠性部件的被动隔振技术进行了大量研究和应用。某卫星飞轮隔振如图1（a）所示。通过抑制飞轮不平衡引起的振动，使卫星姿态稳定度精度提高了1倍。Hubble太空望远镜帆板隔振装置如图1（b）所示，此隔振装置极大地降低了帆板对卫星的干扰。

被动隔振器模型如图1（c）所示［7］。图中：m为隔振对象质量；k为隔振器刚度；c为阻尼系数；x为隔振对象铅直位移；u为基座铅直位移。

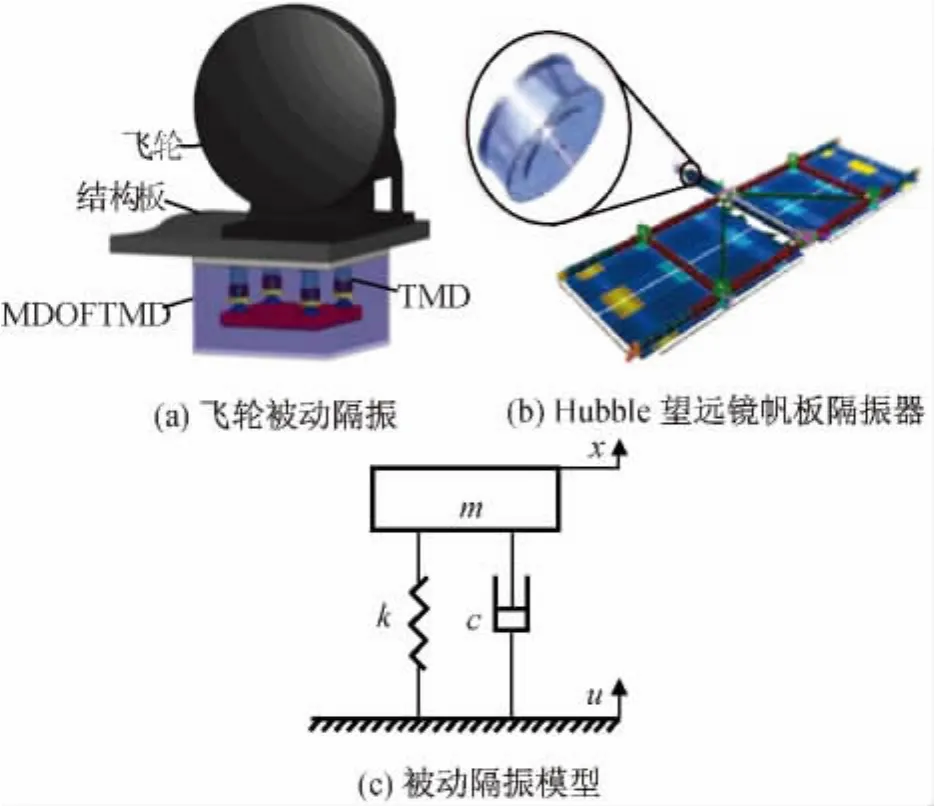
图1 被动隔振器及其模型Fig.1 Passive isolator and model

根据力学定律，被动隔振系统的动力学方程为

对式（1）作拉氏变换，可得被动隔振器的传递函数

式中：ξ为隔振系统阻尼比；ωn为隔振系统固有频率。不同阻尼比下被动隔振器性能计算结果如图2所示。

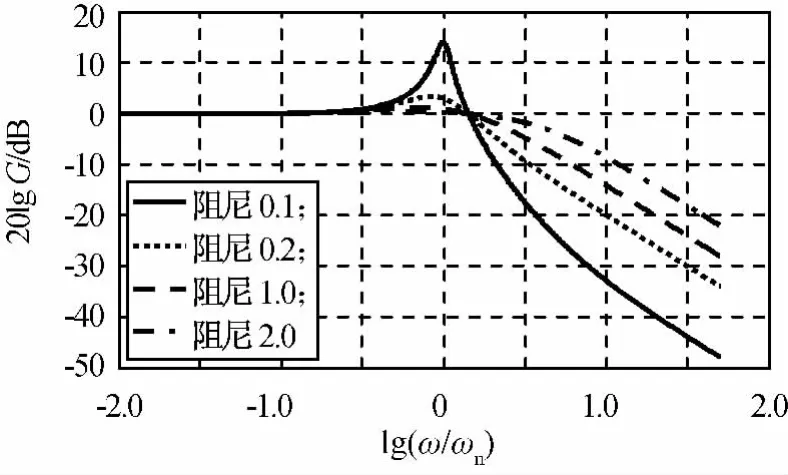
图2 被动隔振器性能Fig.2 Performance of passive isolator

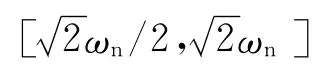
1.2 主动隔振

主动隔振是利用智能作动器进行隔振，是动力学、控制理论、计算机技术、测试和信号分析技术，以及材料科学的综合。它利用控制技术抑制振动，控制需要外界提供能源，主要针对中低频微振动进行抑制。

目前用于载荷振动隔离的典型主动隔振系统主要为多杆并联构形，如正交六杆组成的Stewart平台，结构如图3所示，其隔振频带可到5～100Hz［6］。

主动隔振系统的优点有：能克服被动隔振时低频放大与高频抑制的矛盾，并可根据环境变化随时改变控制算法，克服被动隔振时基座隔振和载荷扰动抑制矛盾。但主动隔振需额外提供能源及测量信息，要求有控制器、作动器、传感器和放大器等，控制系统可能产生不稳定性，且主动隔振失效会使系统失去隔振性能。此外主动隔振还有反馈控制的“水床效应”，即降低某频段干扰时会导致另一频段干扰放大［8］。

图3 基于Stewart平台的主动隔振系统Fig.3 Active isolation based on Stewart system

为克服被动隔振与主动隔振的缺点，本文设计了一种主被动隔振方式。主被动隔振综合了两种隔振的优点，即相对主动隔振减小了能源需要，主动级失效后，被动级仍可提供部分隔振。但若主动控制设计不佳，可能衰减被动隔振性能，且主被动隔振同样达不到完全隔振的效果。

综上所述，采用基于隔振器的平台干扰抑制方法时，干扰源与卫星平台间通过隔振器的接触式安装会导致振动隔而不绝的问题，卫星平台姿态精度难以进一步提高。常规卫星设计中载荷舱的姿态跟随卫星平台进行控制，载荷舱的姿态精度主要取决于卫星平台的姿态控制精度。因此，采用基于隔振器的平台干扰抑制方法无法使载荷姿态精度达到双超性能。

2 双超卫星平台设计方法

针对基于隔振器的平台干扰抑制方法无法满足载荷双超性能，本文设计了一种载荷与振源在空间上完全隔离方法，以达到载荷的完全隔振，实现载荷双超性能。

2.1 动静隔离

将卫星平台设计成相互独立又有机结合的两部分，其一为载荷舱，另一为服务舱，结构如图4所示。

两舱结构上相互独立。载荷舱安装载荷、姿态敏感器（星敏感器、光纤陀螺等），是安静舱段。服务舱安装动量交换执行器（飞轮、力矩陀螺等）、太阳帆板、储箱、推力器等，是嘈杂舱段。两舱间由非接触磁浮机构连接。

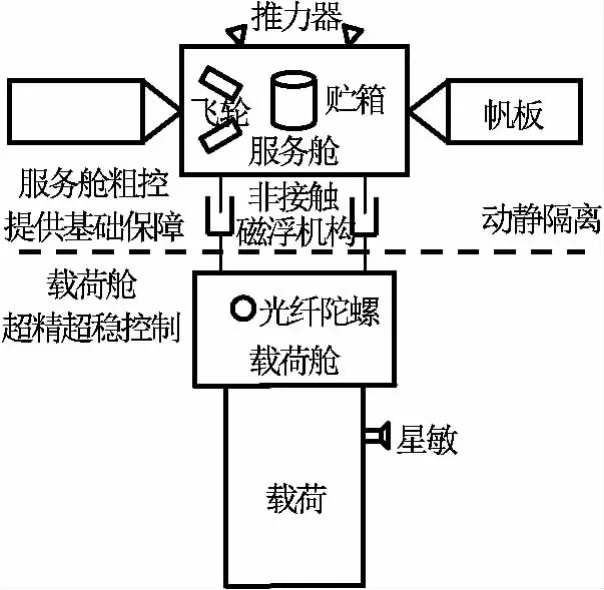
图4 动静隔离、主从协同控制双超卫星结构Fig.4 Configuration of active-quiet isolated and master-slave coordination controlled dual-super satellite

因非接触磁浮机构实现了两舱的非接触，故服务舱振动和干扰不会传输至载荷舱，由此实现有效载荷动中取静，两舱动静隔离。

载荷舱与服务舱由无接触通道或柔性电缆方式实现通信和能源供应，由无接触的相对位置传感器实时测量载荷舱与服务舱间的相对位置与姿态，由非接触的磁浮机构调节姿态和相对位置。

2.2 主从协同控制

双超卫星平台控制逻辑包含载荷舱姿态控制、两舱相对位置控制和服务舱姿态控制，共3个控制回路，如图5所示。与常规平台控制策略不同，双超平台采取载荷舱主动控制，服务舱跟随载荷舱从动控制的主从协同控制策略。其中载荷舱对姿态控制精度要求较高，其姿态反馈信息由姿态敏感器给出；服务舱姿态和两舱相对位置控制对控制精度要求较低，其反馈信息均由相对位置传感器测量信息解算得到。

两舱相对位置控制目的是保证两舱不碰撞，对控制精度的要求相对较低。通过设定相对位置滑模区域阈值，可降低相对位置控制频次，从而减轻磁浮机构压力，使其专注于载荷舱姿态控制。应用滑模间隙非线性控制，实现了“死区”的化害为利。

由于载荷舱无活动和挠性部件，可不考虑挠性部件基频对控制系统带宽的限制，加快系统反应速度，提高控制系统抗干扰性能。另载荷舱可等效为刚体，通过磁浮机构高精度力控性能，使卫星平台具有超高指向精度、超高稳定度的性能。

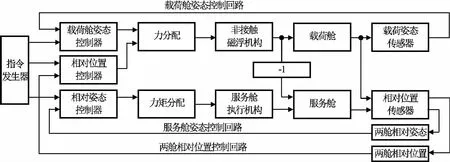
图5 双超卫星控制逻辑Fig.5 Control logic of the dual-super satellite

2.3 双超平台磁浮机构布局方法

为完成载荷舱六自由度运动，实现卫星平台的双超性能，至少需要单自由度执行器6个。

a）基于六杆磁浮机构的双超卫星平台两舱间磁浮机构A1～A6的布局采用Stewart斜拉式形式，如图6所示。

根据磁浮机构的安装位置及布局，可得磁浮机构对载荷舱产生的合力与合力矩。分析发现6个磁浮机构控制力解耦复杂，且任一磁浮机构损坏将导致任务失败，可靠性较低。

b）基于八杆磁浮机构的双超卫星平台结构如图7所示，该平台有磁浮机构8个，且磁浮机构与两舱对接面平行或垂直布置。

图7 8磁浮机构布局Fig.7 Layout of 8maglev devices

根据磁浮机构的安装位置及布局，可得磁浮机构对载荷舱产生的合力与合力矩。分析发现有8个磁浮机构的卫星平台控制力更易解耦，控制更简单，且有冗余备份，提高了系统可靠性。

某磁浮机构出现故障时，磁浮机构产生的合力与合力矩见表1。表中：左侧“×”表示某个磁浮机构故障；右侧“×”表示此合力或合力矩不能实现。

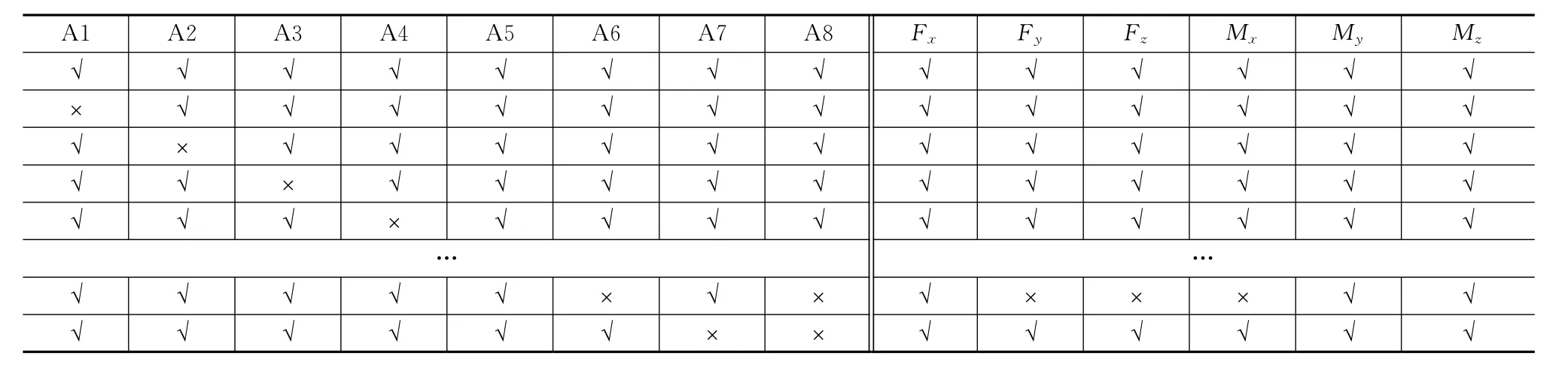
表1 磁浮机构故障模式分析Tab.1 Failure mode analysis of maglev devices

分析发现，当仅有1个磁浮机构故障时，并不影响载荷舱6个自由度的运动；2个磁浮机构故障有28种方式，其中16种不影响载荷舱6个自由度的运动；八杆磁浮机构构型实现了磁浮机构的冗余备份，提高了可靠性。

当前卫星多任务模式要求卫星平台具敏捷机动性能，非接触构型能将载荷舱单独隔离，较传统卫星平台可大幅降低载荷舱的转动惯量，从而提升卫星敏捷能力。此外，考虑磁浮机构线性范围内输出力的能力，还可在载荷舱加装磁悬浮飞轮以增加姿态机动的时效性。

3 仿真分析

载荷舱无活动和挠性部件，可视作刚体进行动力学建模，有

式中：Ip为载荷舱惯量矩阵；ωp为载荷舱角速度；li为磁浮机构相对载荷舱质心的力臂；ΔFAi为磁浮机构输出力误差；Md1为外干扰力矩。

服务舱含活动部件和挠性部件，动力学方程为

式中：Is为服务舱惯量矩阵；ωs为服务舱角速度；hc为飞轮角动量；Caf1，Caf2分别为＋Y、－Y向太阳帆板振动对卫星中心体转动的耦合系数阵；qf1，qf2分别为＋Y、－Y向太阳帆板模态坐标；Mc为飞轮控制力矩；Md2为飞轮动不平衡与挠性部件干扰力矩；Md3为外干扰力矩；Λf为太阳帆板模态频率对角阵；ζf为太阳帆板模态阻尼系数。

对某卫星磁浮机构性能进行姿态仿真，结果如图8、9所示。

由图8可知：载荷舱指向精度为6×10－5（°），姿态稳定度为5×10－6（°）／s，可满足先进航天器双超需求。由图9可知：服务舱指向精度为3×10－3（°），姿态稳定度为1×10－4（°）／s，主要是源于飞轮动不平衡与挠性部件干扰。

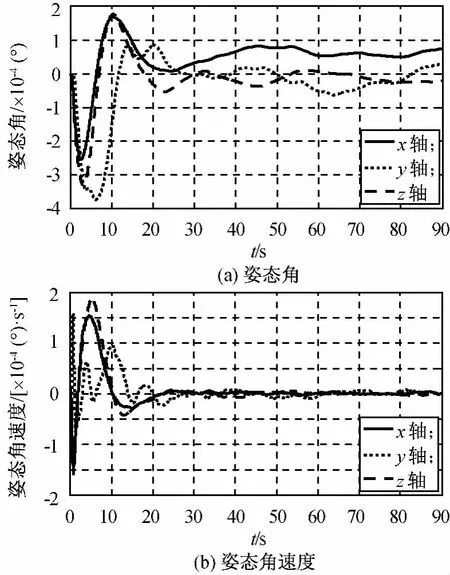
图8 载荷舱姿态角与姿态角速度Fig.8 Attitude angle and angular rate of payload cabin

图9 服务舱姿态角与姿态角速度Fig.9 Attitude angle and angular rate of service cabin

4 结束语

本文针对传统卫星平台设计中干扰抑制方法无法实现完全隔振的不足，提出了一种振源与载荷动静空间隔离、控制主从协同的卫星平台设计方法。采用八杆非接触磁浮机构实现平台动静空间隔离，以消除平台微振动对载荷的干扰；采用载荷为主，平台为辅的协同控制策略，合理有效利用死区的间隙非线性，实现卫星的超精超稳控制。某卫星的磁浮机构性能仿真结果表明：平台满足双超性能。

［1］ PEDREIRO N.Spacecraft architecture for disturbance-free payload［J］.AIAA Journal of Gauidance，Control and Dynamics，2003，26（5）：794-804.

［2］ DEWELLA L，PEDREIROA N，BLAUROCKB C，etal.Precision Telescope pointing and spacecraft vibration isolation for the terrestrial planet finder coronagraph［R］.Proceedings of SPIE，589902，2005.

［3］ PILINSKI E B，LEE A Y.Pointing-stability performance of the Cassini spacecraft［J］.Journal of Spacecraft and Rockets，2009，46（5）：1007-1015.

［4］ BRONOWICKI A J.Vibration isolator for large space telescopes［J］.Journal of Spacecraft and Rocket，2006，43（1）：45-53.

［5］ O’BRIEN J.Micro-precision interferometer pointing control system［R］.JPL 20060035174，1995.

［6］ 刘 磊.航天器主动隔振及精确定向控制技术研究［D］.哈尔滨：哈尔滨工业大学，2011.

［7］ 张士峰，张 辉.高精度测量的被动隔振研究［J］.现代机械，2006（4）：3-5.

［8］ 张丽敏，祖峰磊，邹小军.反馈有源噪声控制系统水床效应的分析与改善［J］.应用声学，2010，29（6）：401-408.