卫星天线双轴驱动机构旋转铰磨损规律研究

张慧博，陈 军，李甘霖，王兴贵，程东起，田 艳

（哈尔滨工业大学（威海）飞行器动力学及仿真研究所，山东 威海 264209）

0 引言

磨损是机械设备失效的主要原因之一，是机械零部件的一种主要失效形式，也是引起其他后续失效的最初原因［1－2］。卫星天线是航天器中实现星地、星间通信与数据传输的重要组成部件，卫星天线驱动机构是实现卫星天线实时跟踪、小范围调姿、定位等功能的一个关键组件［3－4］。双轴驱动机构主要功能是实现卫星天线两自由度的转动，控制天线的精确指向，其指向精度是决定其使用寿命的关键指标。目前航天器的发展趋势是长寿命、高可靠性，卫星的使用寿命由3～5年提高到10～12年，机构磨损变得不可忽视。轴承与轴系间出现磨损间隙，将直接导致卫星天线指向精度下降，严重时将使卫星失效。为分析轴承与轴系间的磨损规律，常将其简化为平面旋转铰，通过动力学仿真与磨损量计算，给出双轴驱动机构旋转铰的磨损规律。但磨损研究很少考虑机构运行中的动态变化，认为磨损率在磨损过程中是不变的，这与实际磨损规律差距较大，故计算准确性较差。为提高磨损计算的精度，出现了以动力学仿真为主，结合磨损实验的磨损规律研究方法：文献［5］用动力学仿真法研究四杆机构的磨损规律；文献［6-7］基于ADAMS动力学仿真，研究磨损规律，提出了磨损寿命仿真预测方法；文献［8］以Virtual.Lab Motion为平台对某履带车辆同步器进行仿真，研究其磨损规律。但由于磨损问题的复杂性，现有研究方法只能根据具体构件进行分析，无通用的磨损规律。另外受实验条件的限制，无法进行微重力条件下的整机磨损实验。为此，本文用仿真法对某空间驱动机构旋转较磨损规律进行了研究。

1 动力学建模与仿真

1.1 运动副间隙描述

含间隙运动副在运行过程中不可避免会发生接触碰撞，这使含间隙系统有两种拓扑状态：一种是不含任何约束的自由运动状态，另一种是单边约束运动状态［9］。含间隙的变结构系统总在自由运动和单边约束两种状态间相互切换，判断系统当前处于的状态，以及对含间隙运动副接触碰撞过程的正确描述，是含间隙动力学建模的关键。

对卫星天线双轴驱动机构旋转铰，间隙Δ用轴承与轴半径之差描述，则

式中：R1为轴承（大圆）半径；R2为轴（小圆）半径。如图1所示。

图1 含间隙转动副模型Fig.1 Revolute joint with clearance

为正确描述接触碰撞过程，判断系统当前处于何种状态，在旋转铰中心处建立坐标系o-xy，设轴的中心坐标为（x1，y1），则接触变形量

由式（2）可知：当δ≤0时，系统处于自由运动状态；当δ＞0时，系统处于单边约束运动状态。

1.2 运动副间隙接触碰撞模型

根据运动副元素的相对运动关系的不同假设，对间隙碰撞问题的处理方法主要有二状态模型、三状态模型、连续接触模型三种。其中二状态模型认为：在运动过程中运动副元素处于分离和接触两种状态，其碰撞特性用无质量等效弹簧阻尼模型描述，该模型假定碰撞为点接触，碰撞力通过接触点作用于两体，碰撞力大小取决于等效弹簧的刚度和阻尼特性。等效弹簧阻尼模型虽然是一种近似分析方法，但它易与机构动力学方程结合，且一般有较好的精度，在含间隙机构动力学分析中应用广泛。

用非线性等效弹簧阻尼模型建立旋转铰间隙接触碰撞模型，其广义形式可表示为

式中：Fn为接触点处法向接触力；Fs为等效弹簧力；Fd为等效阻尼力；K为等效接触刚度；δ分别为运动副元素间的接触变形量和法向相对速度；C（δ）为与δ有关的阻尼因子；m为力指数，由实验确定，通常金属与金属材料碰撞取1.5。

Fn可用Hertz接触模型计算；Fd主要反映碰撞过程的能量损耗特性，同时保证接触力Fn满足碰撞过程的边界条件

式中：Cmax为最大阻尼系数，由实验确定；S（δ）是为防止碰撞过程中阻尼力的不连续引入的函数，且

此处：d为最大嵌入深度，它决定何时阻尼力达到最大；β＝δ／d。

1.3 动力学仿真分析

本文以ADAMS动力学仿真软件为平台，利用虚拟样机技术建立卫星天线双轴驱动机构动力学仿真模型，如图2所示。通过静态校验和运动学校验，保证无间隙虚拟样机的可信性。然后将运动副间隙的接触碰撞模型嵌入动力学模型，用实验确定接触碰撞模型的参数，以保证含间隙双轴驱动机构虚拟样机的可信性。

双轴驱动机构主要由纵轴、横轴两个旋转铰组成，纵轴带动整个驱动机构转动，其旋转铰承受径向力较大。用动力学仿真研究其动态特性，设仿真参数为 间 隙 0.2mm，转 速 3.0 （°）／s，刚 度 1.7×107N／m，阻尼175.0N·s／m，仿真所得运动轨迹、接触变形量、径向速度和接触力分别如图3～6所示。

图2 卫星天线双轴驱动机构虚拟样机模型Fig.2 Virtual prototype model of two-axis-position mechanism for satellite antenna

图3 轴中心运动轨迹Fig.3 Axial center path

图4 接触变形量Fig.4 Deformation

由图4可知：在驱动机构平稳运行时，δ始终大于0，则旋转铰中轴与轴承处于连续接触状态。由图6可知：接触力为周期变化，且幅值较小，旋转铰周向受力相对均匀，可取接触力的平均值作为该工况下的旋转铰受力，同时近似认为旋转铰处为均匀磨损。

图5 径向速度Fig.5 Radial velocity

图6 接触力Fig.6 Contact force

接触力平均值随磨损间隙而变，在磨损过程中的变化规律是计算磨损量的动力学基础。因假设旋转铰为均匀磨损，改变运动副间隙以模拟磨损间隙变化，进行动力学仿真实验，得到不同磨损间隙的接触力平均值如图7所示。

图7 接触力变化规律Fig.7 Contact force variation

由图7可知：运动副间隙随着机构的磨损不断变大时，旋转铰接触力近似成线性增大。由多项式拟合，额定工况下双轴驱动机构纵轴旋转铰处接触力

2 磨损数学模型

磨损过程是一个极其复杂的过程。现阶段的磨损机理研究不充分，对磨损过程很难建立详细的数学模型。对于运动副磨损的研究，多是根据实验确定磨损的宏观规律，用磨损率和各因素之间的简单函数关系表达。根据摩擦学理论同时结合相关的磨损实验，可建立磨损过程的数学模型，磨损率γ可表示为

式中：W为磨损量；t为磨损时间；P为摩擦面的表面接触压力；V为运动副构件间的相对速度；Tk为摩擦表面温度；Kw为摩擦表面形态、润滑状态及材料特性等因素［5］。为研究磨损量的极限值，认为磨损在干摩擦条件下进行，忽略润滑、温度等因素的影响。根据当前干摩擦较为通用的磨损率表达式，可得经验公式

式中：Kw，m，n为与材料特性有关的参量，由实验获得［10］。则磨损量可表示为

相应的磨损深度

式中：ρ为材料密度；S为磨损面积。

根据磨损深度的函数表达式和接触力变化函数，可建立磨损过程的数学模型。为提高计算速度，采用分段近似方法，在一个时间积分段中将压力和速度作为常数处理。建立数学模型

式中：N为运行次数，N≥1，取旋转铰相对转动1周为运行1次；ΔN为运行N次的磨损间隙（Δ0为初始间隙）；hN为运行第N次的磨损深度；S＝2π（R＋ΔN－1）b；R为旋转铰处轴承内径；b为轴承宽度；p（ΔN－1）为间隙为ΔN－1时的接触力；v为轴与轴承的相对速度，由卫星天线的运行工况决定；T为积分时间，即运行1次的时间。

根据数学模型，在MATLAB软件中编制程序，进行递推运算，可得与运行次数N相关的磨损间隙的变化规律。将N换算为时间，即为驱动机构运行过程中的磨损规律。

3 旋转铰磨损规律分析

结合接触力变化函数和磨损数学模型，研究双轴驱动机构纵轴旋转铰的磨损规律。设磨损参数为：T＝120.0s；m＝1.5；n＝2.0；Kw＝0.92；Δ0＝0.05mm，仿真所得磨损过程如图8所示。

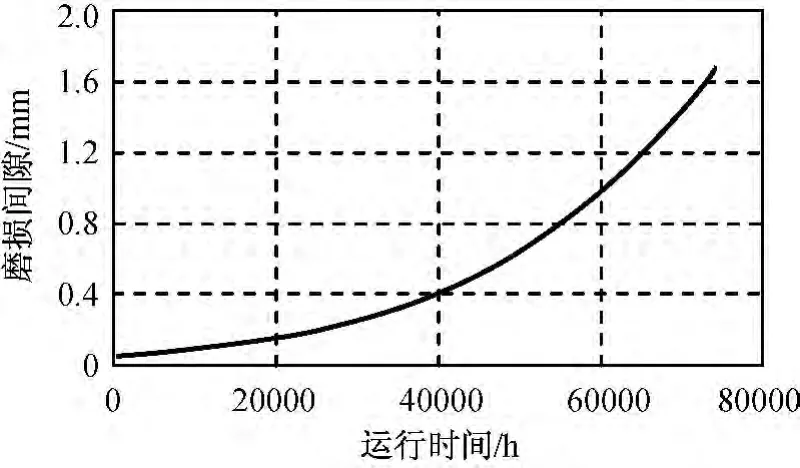
图8 磨损过程Fig.8 Wear curve

由图8可知：在运行初期，运动副间隙小，接触力较小，磨损率基本保持不变，处于稳定磨损阶段，此时机构运行稳定，驱动机构指向精度能得到保证；运行一段时间后，磨损量不断累加，运动副间隙增大，接触力随之增大，导致磨损率迅速增加，磨损越来越剧烈，工作条件急剧恶化，这对驱动机构的位置误差、姿态误差及速度误差都有影响，会导致卫星天线指向精度迅速下降，甚至卫星天线完全失效。因此，根据驱动机构旋转铰的以上磨损规律，可进行合理的机构设计和控制系统设计，尽可能降低磨损间隙变化对系统运行的影响，保证卫星天线指向精度。

4 结束语

本文对某卫星天线双轴驱动机构旋转铰的磨损规律进行了研究。用虚拟样机技术建立并验证无间隙整机模型，结合构件的接触碰撞实验和磨损实验，建立合理的旋转铰接触碰撞模型和磨损模型。将接触碰撞模型嵌入虚拟样机，保证含间隙虚拟样机的可信性。用动力学仿真研究了旋转铰的动态特性及接触力在磨损过程中的变化规律，给出了旋转铰的磨损规律。在虚拟样机建立合理，并有构件的接触碰撞实验和磨损实验作为支持的情况下，可保证磨损规律的可信性。该方法降低了实验难度，所得的磨损规律可为双轴驱动机构的性能评估与优化设计提供指导。

［1］ 刘英杰，成克强.磨损失效分析［M］.北京：机械工业出版社，1991.

［2］ 任 和，冯元生，贾少膨.机构磨损的模糊可靠性计算研究［J］.机械科学与技术，1998，17（1）：46-48.

［3］ 孙 京，马兴瑞，于登云.星载天线双轴定位机构指向精度分析［J］.宇航学报，2007，28（3）：545-550.

［4］ 田 浩，赵 阳，孙 京，等.双轴定位点波束天线波束指向计算［J］.宇航学报，2007，28（5）：1215-1218.

［5］ FLORES P.Modeling and simulation of wear in revolute clearance joints in multibody syste-ms［J］.Mechanism and Machine Theory，2009，44：1211-1222.

［6］ 张景柱，徐 诚，胡良明，等.基于ADAMS的操纵摩擦件寿命仿真预测方法［J］.机械科学与技术，2007，26（6）：767-769.

［7］ 张箭锋，郑 坚，马吉胜.基于ADAMS的某型炮闩系统关键件磨损寿命计算［J］.机械工程与自动化，2009（5）：114-118.

［8］ 王 炎，王玉军，张 磊，等.某履带车辆同步器工作过程仿真及磨损寿命预测［J］.军械工程学院学报，2009，21（6）：26-30.

［9］ ZHAO Y，BAI Z F.Dynamics analysis of space robot manipulator with joint clearance［J］.Acta Astronautica，2010，10：1016-1025.

［10］ 温诗铸，黄 平.摩擦学原理［M］.北京：清华大学出版社，2008.