InSAR编队卫星全零多普勒姿态导引研究

槐 超，王文妍

（上海航天控制技术研究所，上海 200233）

0 引言

SAR卫星的多普勒特性是决定雷达方位向性能的主要因素，直接影响雷达方位向分辨率、PRF的选择。多普勒中心频率不准确将降低信噪比，增加方位模糊度，出现输出图像位置偏移，影响图像的定位。在星载SAR中，由于地球曲率及自转的存在，导致多普勒中心偏移，典型的偏移值远高于系统脉冲重复频率［1］。除采用杂波锁定等直接估计回波信号多普勒中心的方法解决多普勒中心偏移外，还可在数据阶段进行获取处理，偏航导引等导引方法即基于此思路。通过对卫星合理的姿态导引，降低多普勒中心频率，简化后期图像处理过程。

单星SAR姿态导引角的推导均由卫星发射信号的多普勒历程出发，得出回波信号中回波延迟产生的相位关系，进而推导多普勒中心频率的公式［2］。此公式是卫星和地面目标相对位置、速度关系的函数，而卫星的相对位置、速度关系则隐含了卫星的姿态角信息。通过分析公式，找出合理的姿态角，降低多普勒中心频率。文献［3-4］对降低多普勒中心的导引方式进行了研究，分别提出偏航导引和二维导引方式，并在卫星工程中应用，但此两种方法均未能准确分析全零多普勒产生的原因，因此无法实现理论上的全零多普勒导引，当未来的卫星成像质量的要求越来越高时，其应用可能会受局限。

InSAR编队是由数颗SAR卫星组成的卫星编队系统。在系统中，主从星间保持一定的空间构形，形成合理的测量基线，协同工作实现单星SAR系统难以完成的地形高程测量、动目标检测等任务。对双星InSAR编队，主星发射电磁波、主从星同时接收电磁波。主星信号的多普勒历程与传统单星SAR相同，因此多普勒中心频率的计算公式也将相同，可用传统的姿态导引方法。但对从星，接收到的是由主星发射、经地面目标点反射回从星的信号，多普勒历程发生了变化，相应的多普勒中心频率的计算公式也有变化。在此状况下，原姿态导引方法对从星的适用性亟待论证，但相关研究较少。

本文对InSAR编队卫星全零多普勒姿态导引进行了研究。

1 InSAR从星多普勒中心频率

1.1 从星多普勒中心频率

如图1所示：S1为主星，S2为从星，T为地面目标。S1发射的电磁波经T反射到S2。设RS1（t），RS2（t）为卫星位置矢量；RT（t）为地面目标随时间t变化的位置矢量，则雷达与地面目标的斜距

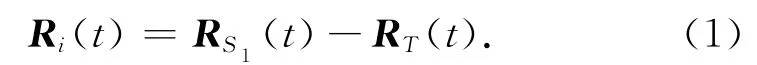
式中：i＝1，2，分别代表主星和从星。

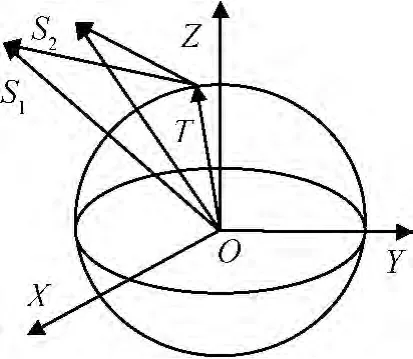
图1 双星编队工作模式Fig.1 Operation mode of InSAR formation

分析SAR回波信号相位历程时，对一个孔径时间内的信号，令波束中心照射目标的时刻t＝0，则有

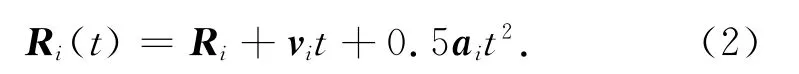
式中：Ri，vi，ai分别为t＝0时两颗卫星与地面目标的相对距离、速度和加速度，且

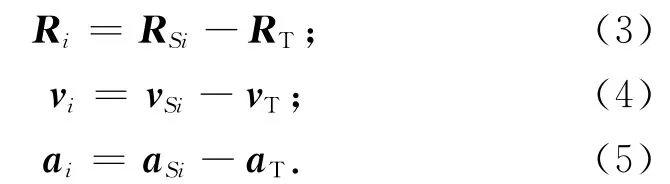
此处：RSi，vSi，aSi分别为t＝0时的卫星位置、速度和加速度；RT，vT，aT分别为t＝0时的目标位置、速度和加速度。

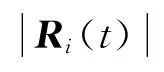
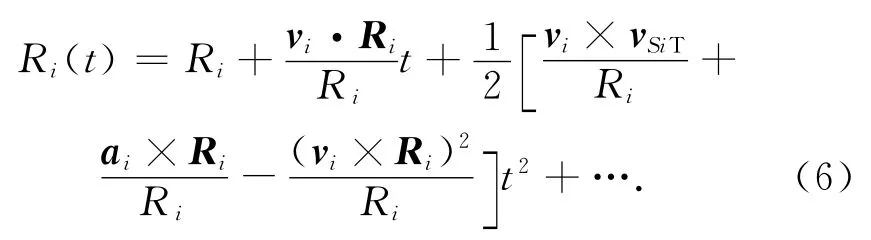
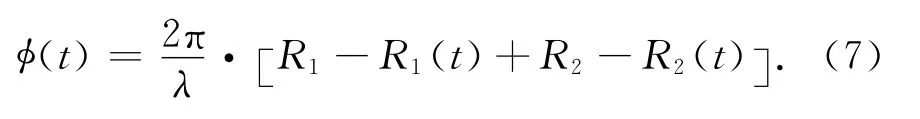
式中：λ为波长。瞬时频率

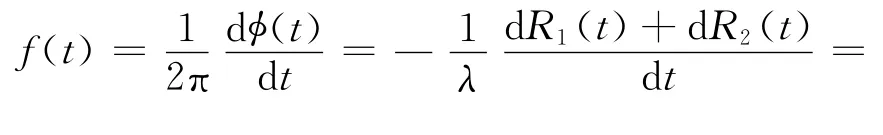
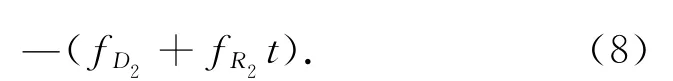
式中：fD2为从星的多普勒中心频率，且

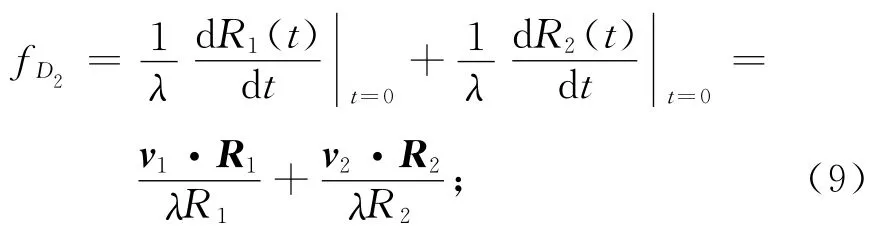
fR2为从星的多普勒调频率，与姿态导引角的导出无关；λ为波长。

1.2 从星多普勒中心频率分析

主星多普勒中心频率

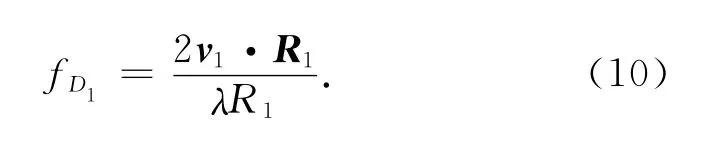
回波信号的不同相位产生不同的多普勒中心频率，由式（9）、（10）可知：对收发信号均在同一星上的主星，多普勒中心频率和主星与目标点的相对位置、相对速度有关。对接收主星发射信号的从星，多普勒中心频率则不但与从星与目标点的相对位置、速度有关，而且与主星相对目标点的位置、速度有关。

对单星来说，推导全零多普勒姿态导引角时，一般是找到fD1与欧拉角的关系，进而推导出合理的姿态导引角尽量降低fD1，最好令其为0。对In－SAR中的从星，由式（10）可知：多普勒中心频率与主星和从星的姿态均有关。但两者的表达形式极类似，有

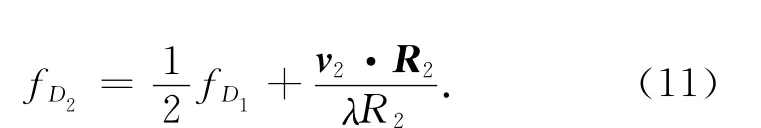
由式（11）可知：若主星采用全零多普勒导引方法，则第一项为0；若从星采用与主星推导方式相同的导引方法，则可使第二项为0，此时从星的多普勒中心频率fD2＝0，故从星采用的导引方式可称为全零多普勒姿态导引。若主星无法实现全零多普勒导引，即使从星采用全零多普勒导引的方式，从星的多普勒中心频率也不能为0。上述分析从理论上证明了InSAR编队中，主从星同时采用全零多普勒导引方法的可行性与正确性。

2 全零多普勒中心频率姿态导引

2.1 偏航和俯仰导引角解析表达式

设卫星相对地心的位置和速度分别为Rs，vs，地面目标相对地心的位置和速度分别是Rs，vs，地球自转的角速度为ωe，则可得卫星的多普勒中心频率

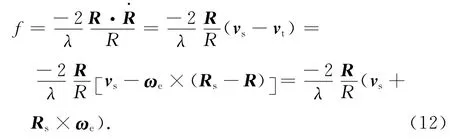
为计算姿态导引角，定义卫星本体坐标系，设初始时刻卫星本体坐标系与轨道坐标系重合：原点在卫星质心；Z轴由卫星质心指向地心；X轴在轨道平面内，垂直于Z轴，指向卫星速度方向为正（因存在航迹角，X轴向与真实的卫星速度方向并不一致）；Y轴由右手定则确定。另令ix，iy，iz分别为X、Y、Z轴的单位矢量；X、Y、Z三轴分别称为滚动轴、俯仰轴和偏航轴。

卫星未进行姿态导引时，在体坐标系中有

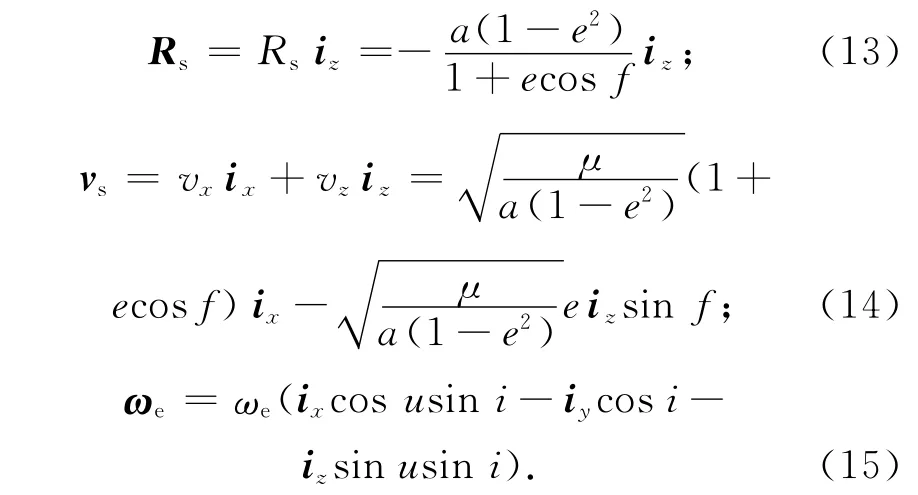
式中：u为纬度幅角［5］。此时，有

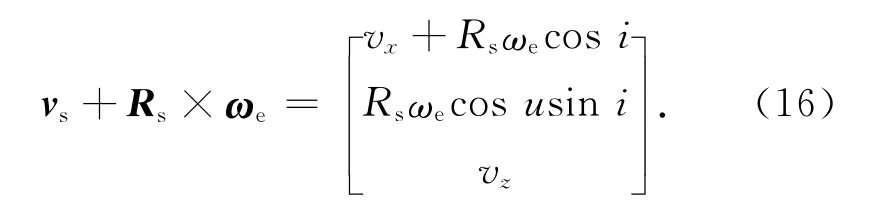
当对卫星进行偏航和俯仰导引后，设偏航角为ψ，俯仰角为θ，在卫星本体坐标系中有

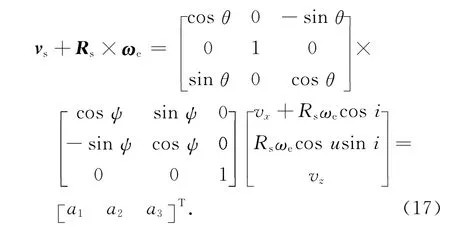
式中：a1＝cosθcosψ（vx＋Rsωecosi）＋cosθ×sinψRsωecosusini－vzsinθ；a2＝－sinψ（vx＋Rsωecosi）＋cosψRsωecosusini；a3＝ sinθ×cosψ（vx＋Rsωecosi）＋sinθsinψRsωecosusini＋vzcosθ。

SAR天线中心相对于目标点的位置矢量R在卫星本体系中表示时，仅与SAR天线的安装方式有关。假设SAR天线安装在本体系的YOZ平面上，方向与X轴垂直，下视角为α（即天线中心与Z轴的夹角为α）。此时，进行偏航和俯仰导引后，有

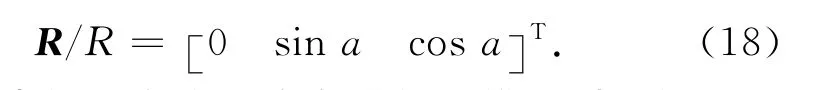
则式（12）中的所有变量均在进行二维导引后的卫星本体系中表示，有

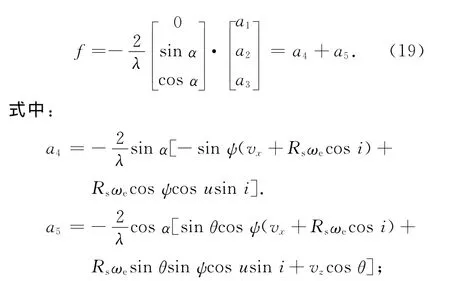
分析式（19），欲使全零多普勒导引与下视角无关，即SAR天线距离向的天线中心始终指向零多普勒线，只需满足

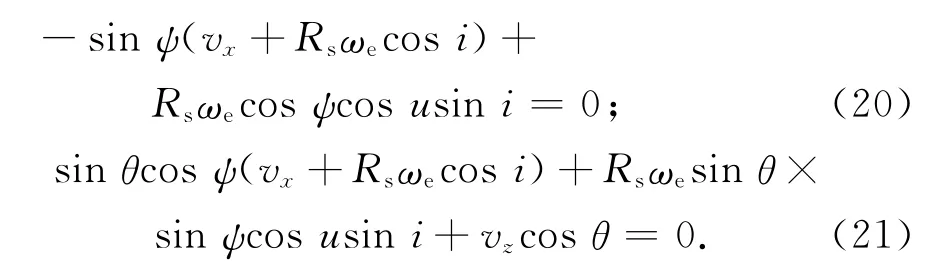
对求解式（20）、（21），可得

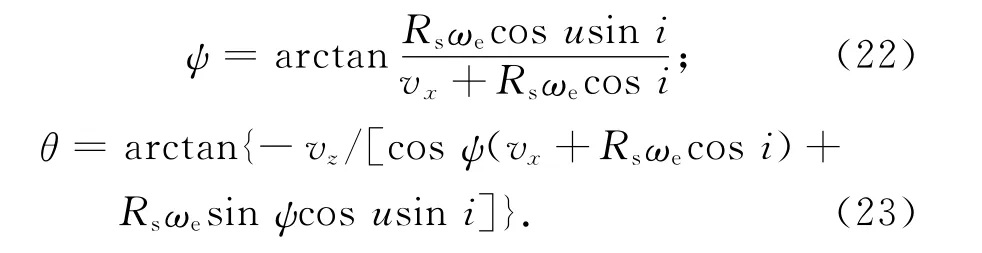
式中：

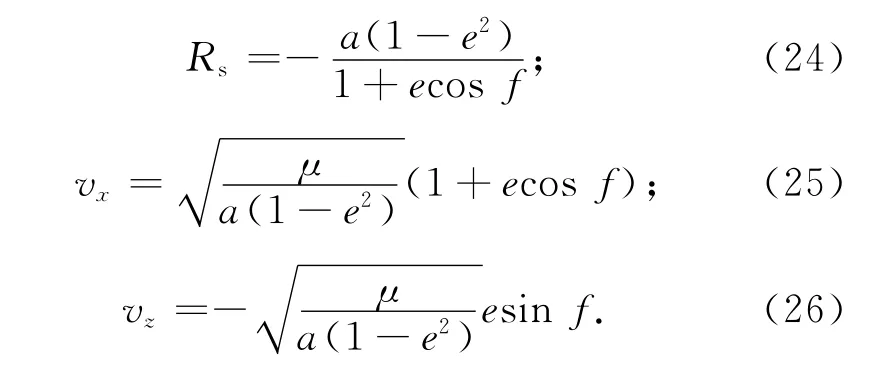
由上述分析可知：理论上按以上方法对偏航角和俯仰角进行二维导引，在距离向上SAR天线中心始终指向零多普勒线，无多普勒残余，可实现全零多普勒姿态导引。

当e＝0时，椭圆轨道变为圆轨道，式（22）可简化为

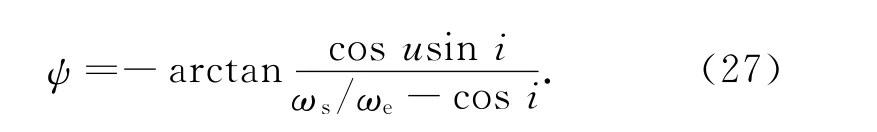
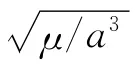
2.2 仿真

为验证本文所推导的全零多普勒中心频率导引方法的有效性，取仿真参数为：半长轴7 000km，偏心率0.001，轨道倾角97.43°，升交点赤径85°，近地点 幅 角 90°，在 下 视 角 分 别 为 20°／35°／50°，波 长0.031m。

文献［3］因轨道SAR偏航导引方法的仿真结果如图2所示；文献［4］提出的全零多普勒中心频率导引方法的仿真结果如图3所示，这种导引方法也是现今卫星中普遍使用的；本文方法所获得的结果如图4所示，仿真显示此方法将多普勒中心频率降低到了10－10量级，误差是由计算机计算误差引起的，理论上为0。本文提出的导引方法能真正获得全零多普勒中心频率，且与真近点角和下视角无关。

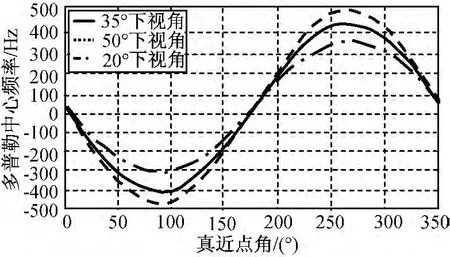
图2 文献［3］方法结果Fig.2 Simulation result of method in reference 3

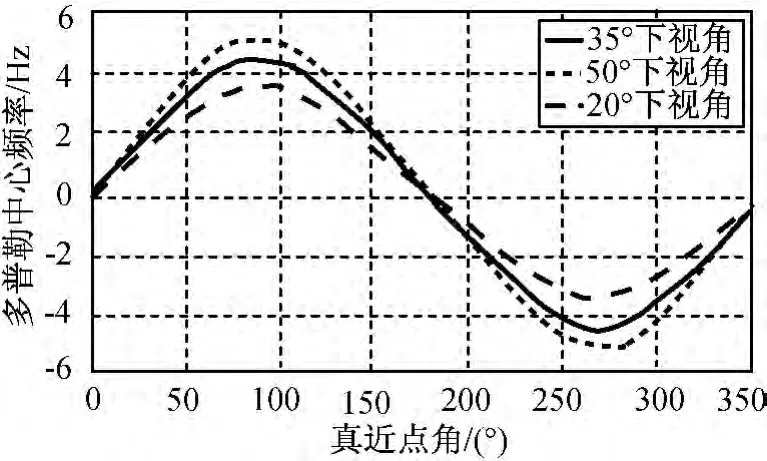
图3 文献［4］方法结果Fig.3 Simulation result of method in reference 4

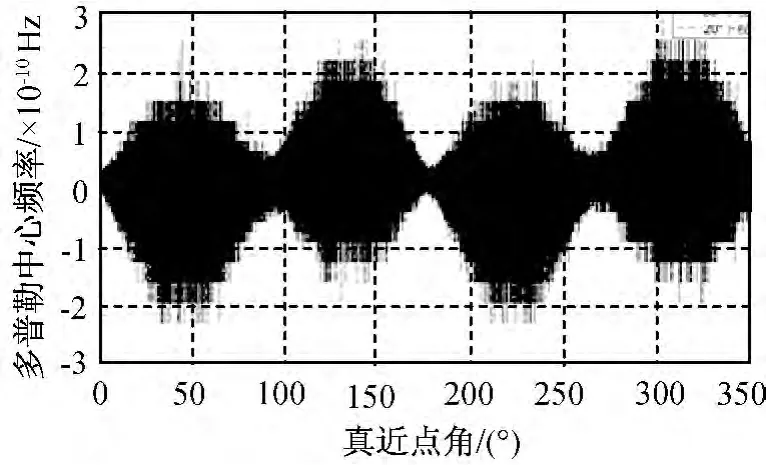
图4 本文方法结果Fig.4 Simulation result of method in 3this paper

需要指出，以上仿真未加入轨道与姿态控制误差。应用本文轨道参数仿真可得控制误差对多普勒中心频率的影响结果见表1。其中：三轴姿态误差均选为0.01°，轨道误差采用轨道半长轴1 000m。

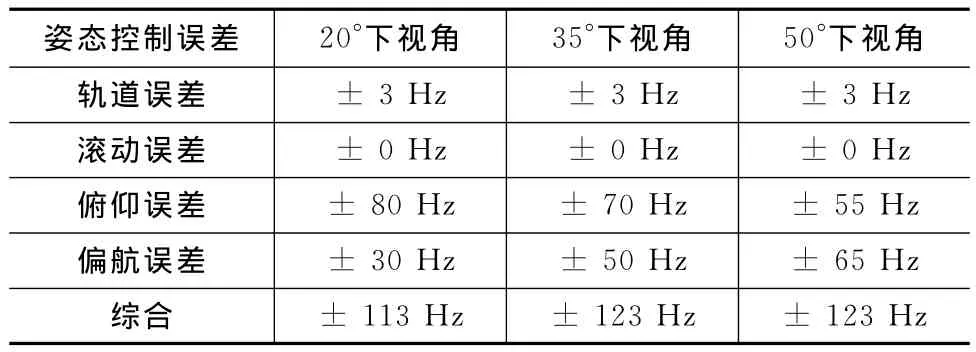
表1 控制误差引起的残余多普勒中心频率Tab.1 Residual Doppler centroid due to control error

由表1可知：控制误差会对多普勒中心频率造成较大的影响。甚至从某种程度上抵消了本文全零多普勒导引方法的优越性。因此，为获得更好的图像质量，还需进一步提高卫星控制精度。

3 结束语

本文对InSAR编队卫星全零多普勒姿态导引进行了研究，从理论上论证了InSAR编队中，主从卫星均采用全零多普勒导引的可行性与正确性。研究发现在InSAR编队中，当主星无法实现全零多普勒导引时，即使从星进行全零多普勒导引，从星的多普勒中心频率也无法为零。提出了一种精确的全零多普勒中心频率导引方法，推导了二维姿态导引角的解析表达式，并通过对比仿真验证该方法的精确性。该研究对InSAR编队系统的二维导引方式具有理论和工程指导意义。

［1］ 张永俊，黄海风，张永胜，等.椭圆轨道全零多普勒导引律研究［J］.电子与信息学报，2010，32（4）：937-940.

［2］ 魏钟铨.合成孔径雷达卫星［M］.北京：科学出版社，2001.

［3］ RANEY R K.Doppler properties of radars in circular orbits［J］.International Journal of Remote Sensing，1986，7（9）：1153-1162.

［4］ FIEDLER H，BOERNER E，MITTER J，etal.Total zeros Doppler steering-a new method for minimizing the Doppler centroid［J］.IEEE Geosci Remote Sens Lett，2005，2（2）：141-145.

［5］ 章仁为.卫星轨道姿态动力学与控制［M］.北京：北京航空航天大学出版社，1998.