基于木星借力的太阳极轨探测器轨道设计方法

董泽政，李绿萍，张靖沛，张 嵬，陈昌亚

（1.上海卫星工程研究所，上海 200240；2.上海航天技术基础研究所，上海 201109）

0 引言

太阳是距离地球最近的恒星，也是支撑人类活动的最重要能源。对太阳进行全方面、深入观测，进一步提高人类对太阳的认识有重要的现实意义。太阳极轨探测器运行于日心大倾角轨道，可飞抵太阳两极区域并绕行运转，对太阳表面实现全方位的观测，对了解太阳活动分布和演化有重要意义。美国于1990年10月发射了尤利西斯探测器，在轨服役近17年，尤利西斯探测器发回的数据进一步加深了科学家对太阳的认识，对探测太阳两极做出重要贡献。

日心大倾角轨道设计方法是实现太阳极轨探测的前提。与一般深空轨道不同，日心大倾角轨道并非以某行星作为目的地，而以特定日心轨道为目标，由此产生实现的特殊性。目前，国内外对日心大倾角轨道设计方法的研究并不多，尤利西斯探测器的参考轨迹特征报告中有所提及，但仅限对轨道设计结果的描述，未提供可行的设计方法［1，5］。本文对日心大倾角轨道的实现方式和借力方案进行了分析，研究了步轨道设计方法。

1 日心大倾角轨道实现方式

分析地球直接发射和不同行星借力方式下实现日心大倾角轨道对运载能力的要求和可能性。考虑地球直接发射的方式，如图1所示。

以黄道面夹角60°～90°为目标倾角，从地球直接发射，所需速度增量

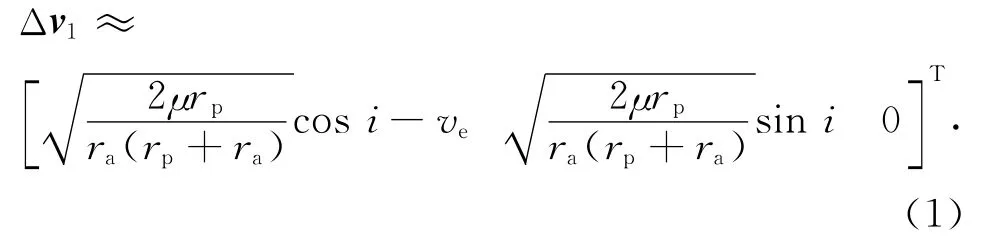
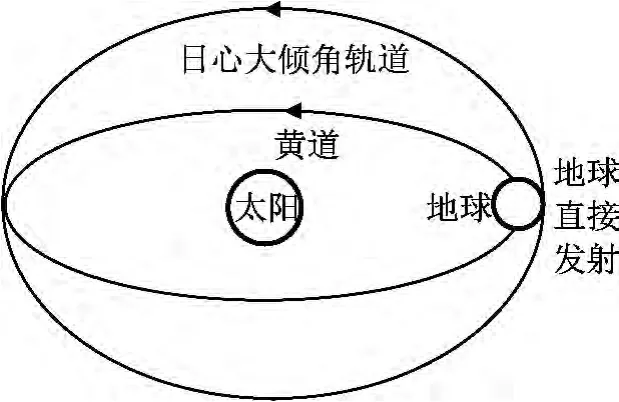
图1 地球直接发射进入日心大倾角轨道Fig.1 Geometry of larger inclination heliocentric orbit launched from earth directly

式中：μ为太阳引力常数；rp为目标轨道近点日心距；ra为目标轨道远点日心距；i为目标轨道倾角；ve为地球公转速度，据此得到地球直接发射C3与rp，i的关系如图2所示。图中：C3为地球逃逸速度v∞的平方。由图2可知：若从地球直接发射，实现日心大倾角轨道的C3需求为700～1 400km2／s2，远超出目前运载火箭的实际能力，即目前技术条件下从地球直接发射进入日心大倾角轨道是不可行的。应考虑通过行星借力方式实现（如图3所示），从地球发射探测器，使之与某行星交会，通过飞越行星过程中的“借力效应”获取大倾角轨道所需的速度增量。

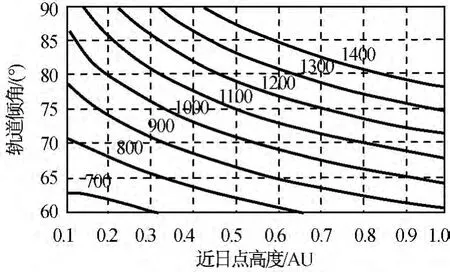
图2 地球直接发射下实现日心大倾角轨道对运载能力C3要求Fig.2C3requirement to larger inclination heliocentric orbit launched from earth directly

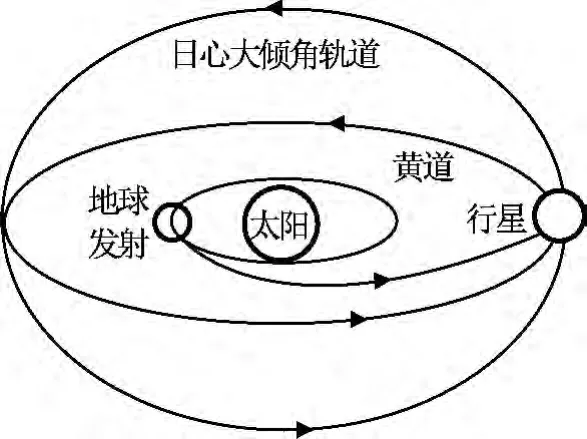
图3 行星借力进入日心大倾角轨道Fig.3 Geometry of larger inclination heliocentric orbit by planet gravity-assists

太阳系各大行星的公转轨道基本参数见表1。

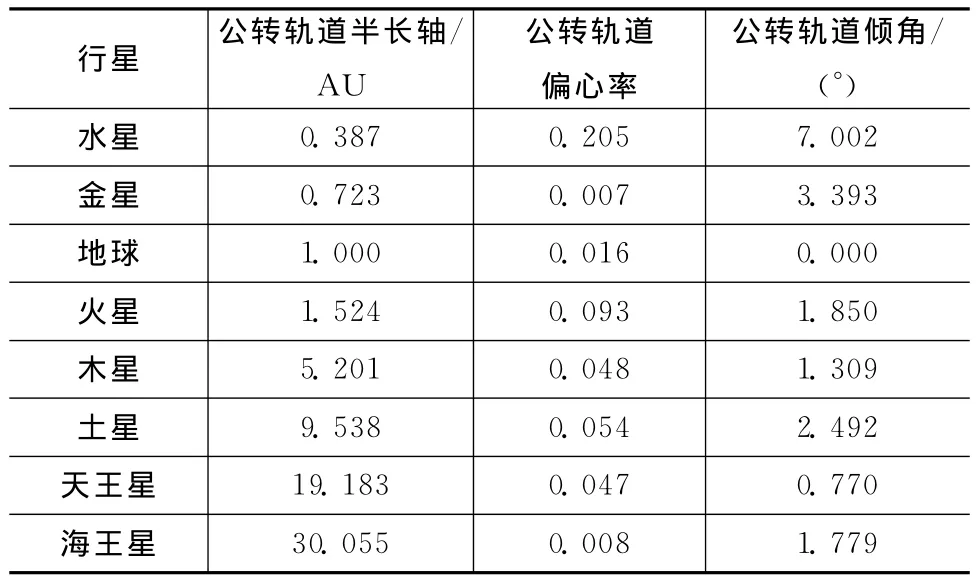
表1 太阳系各大行星公转轨道参数Tab.1 Heliocentric orbit parameters of solar system planets

由表1可知：除水星外各行星运行轨道倾角均小于3°，水星倾角也不足8°。从地球发射至其他行星的探测器星际转移轨道将近似于黄道面，类似于地球发射，不同行星借力实现日心大倾角轨道的速度增量

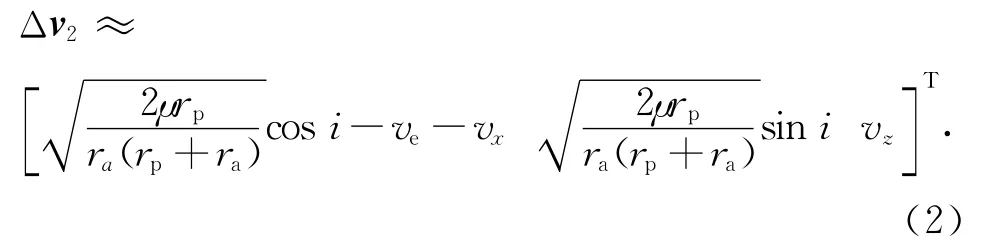
式中：［vx0vz］T为探测器飞越前的速度矢量。由此可粗略计算出不同行星轨道借力进入日心大倾角轨道所需速度增量见表2。

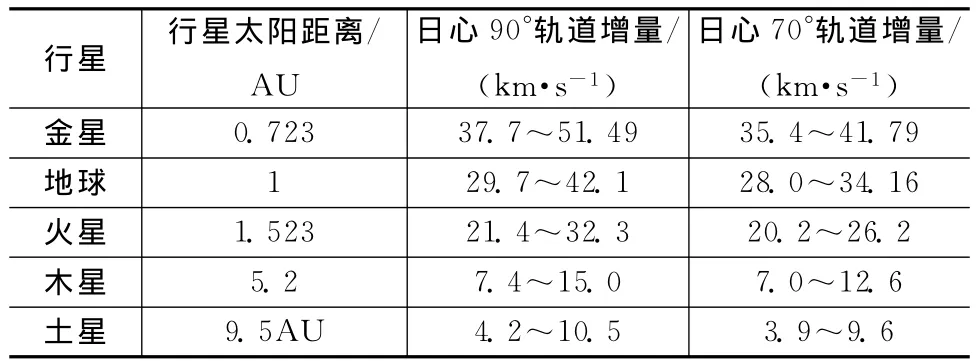
表2 不同天体借力进入日心大倾角轨道的速度增量需求Tab.2 Δvrequirements of larger inclination heliocentric orbit by different planet gravity-assists

根据文献［1，2］，行星飞越速度增量

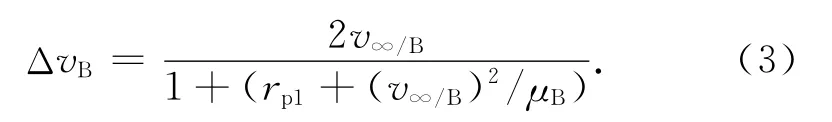
式中：v∞／B为探测器与飞越星体的相对速度；rp1为飞越轨道的近心点半径；μB为飞越天体的引力常数。实际上rp1存在最小值，当rp1为飞越星体半径（或大气层半径）时，ΔvB取局部最大值，进一步分析可知当v∞／B与借力天体的第一宇宙速度相等时，可得ΔvB的最大值，且其数值与第一宇宙速度相等。当rp1取最小值时，由式（3）可得不同v∞／B下各星体提供ΔvB如图4所示。

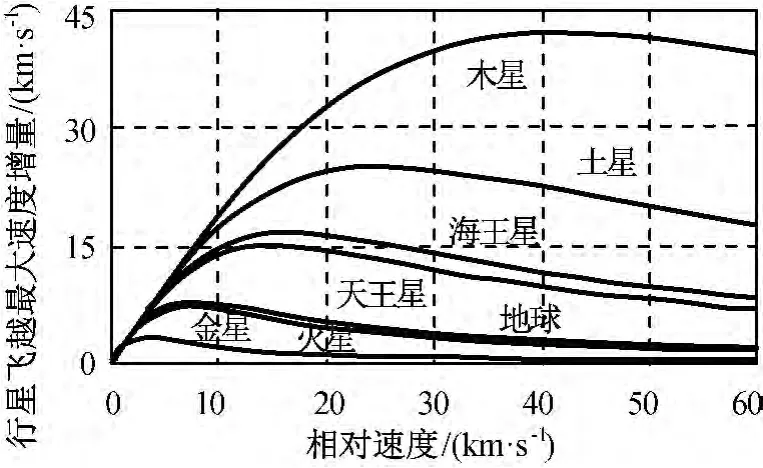
图4 不同相对速度时行星借力最大速度增量Fig.4 MaximumΔvunder various relative velocity of planet gravity-assists

比较图2、表2可知：金星、地球和火星能提供的最大速度增量无法满足日心大倾角轨道转移需求；木星和土星可满足速度增量需求。若选择的借力天体越远，运载发射负担越重，任务实施时间越长，因此建议选择木星作为飞越天体，以获得日心大倾角轨道所需的速度增量。

2 轨道设计

采用地球发射木星飞越的方式实现日心大倾角轨道，轨道设计将包括地球－木星转移轨道和木星借力轨道两部分。

2.1 星际转移轨道设计

探测器通过运载工具提供速度增量，从地球逃逸并经日心轨道运动至木星周围。这类典型的星际转移轨道设计可通过兰伯特问题解决：给定两点位置矢量r1，r2及转移时间Δt，可确定转移轨道的飞行轨迹。工程实际中，习惯将地球发射时间t0、木星借力时间tf作为设计变量，由此根据星历计算出地球和目标天体的空间位置，完成转移轨道设计。具体可表示为

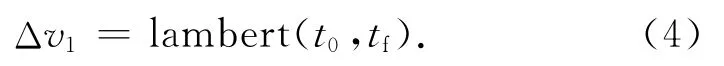
式中：lambert（t0，tf）为兰伯特问题求解，具体可参见文献［3］。通过求解兰伯特问题，可算出地球逃逸所需C3能量及木星进入日心速度vin，这两个参数将分别作为地球逃逸轨道设计和木星借力轨道设计的输入。

2.2 木星借力轨道设计

为便于日心大倾角轨道设计，建立如图5所示木星借力坐标O-XYZ：坐标系原点O位于木星；OX轴指向为借力时木星相对太阳的矢量；OZ轴垂直木星公转轨道面；OY轴与OX、OY轴构成右手系，指向木星前进方向。

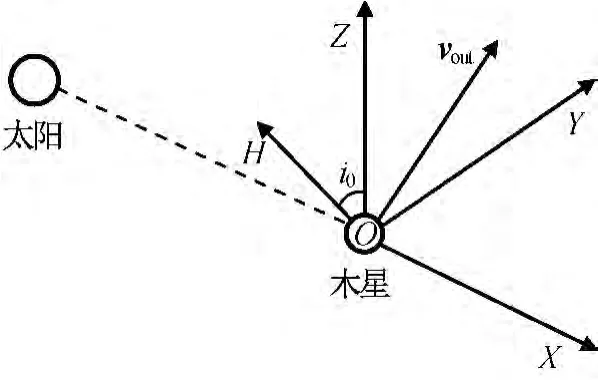
图5 木星借力坐标系Fig.5 Reference system of Jupiter gravity-assist

木星公转轨道倾角较小（iJ≈1.309°），XOY平面近似于黄道面，另忽略木星影响球的影响。在O-XYZ坐标系中，探测器沿日心地木转移轨道到达木星附近的相对速度vin已知，而借力后日心速度vout是目标轨道倾角i0、近日点日心距rp0、远日点日心距ra0、近日点幅角ω0和真近点角θ0的函数。定义vout的分量形式可表示为

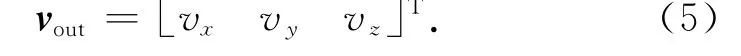
式中：vx，vy，vz分别为借力后日心速度vout在O-XYZ系OX、OY、OZ轴方向的分量，且

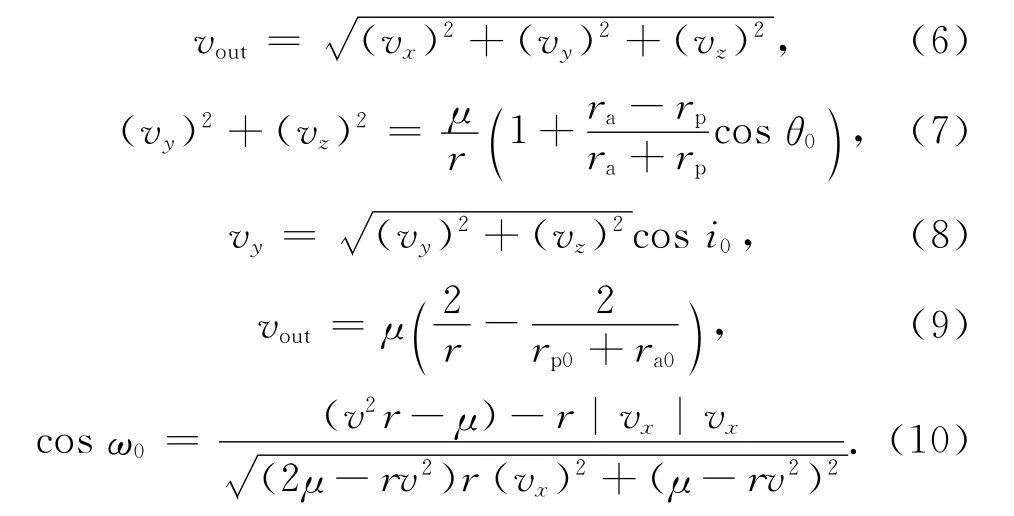
若探测器地木转移轨道ra0与木－日距离r接近时，可认为θ0≈180°，而探测器地木转移轨道近日点接近黄道，即ω0≈0°，180°。由此可算得探测器日心速度vout的分量为

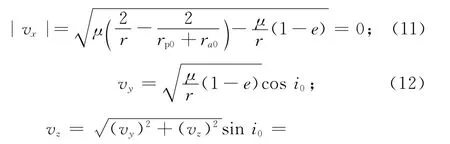
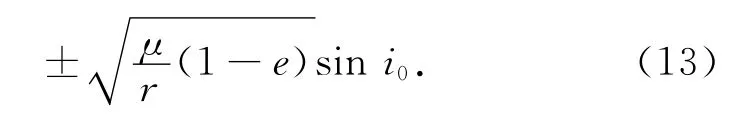
式中：e为木星公转轨道的偏心率。

据此可得飞越后的木星相对速度

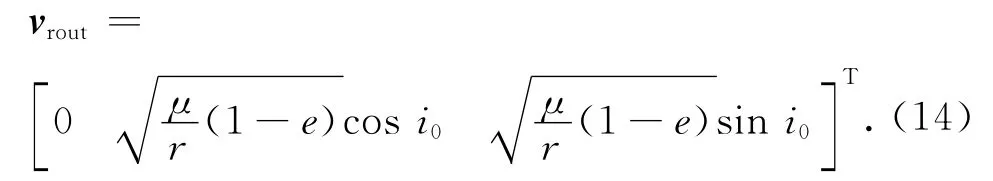
同样，飞越前木星相对速度

则由飞越前后的相对速度矢量vrin，vrout，可计算木星飞越的近木点木心距离和倾角，具体如下：为实现进出木星相对速度vrin，vrout的大小相等，假设在近木点位置存在一个脉冲机动，木星借力几何如图6所示。图中：真实运动轨迹由脉冲前后的两条双曲线轨道轨迹拼接而成。两条轨迹的近地地心距相同。在近地点进行深空机动（DSM）的原因是此时探测器动能最大，相同的速度增量可获得最多的能量增加。由图6可知：速度变化角度α可分为α1，α2两部分，分别为过近地点前后的速度方向变化角度。由文献［4］，

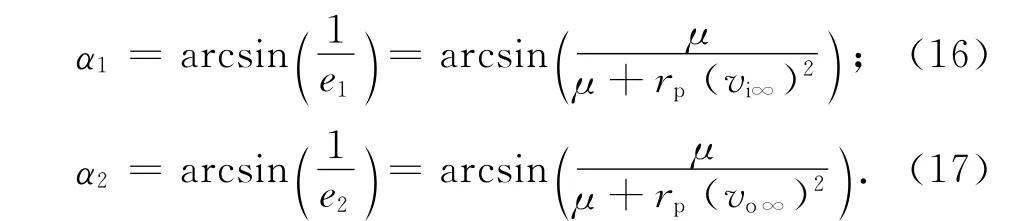
式中：vi0，vo∞分别为进出木星相对速度vrin，vrout的大小。由此可得相对速度的变化角

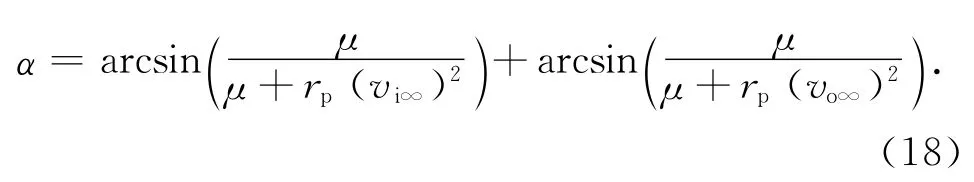
由式（18）用迭代算法可解出rp。

对双曲线轨道长半轴a大小取决于剩余速度v∞，即进出木星相对速度vrin，vrout的大小，有

图6 木星借力几何描述Fig.6 Geometry of Jupiter gravity-assist

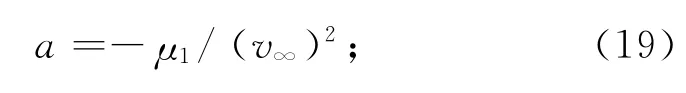
能量式为

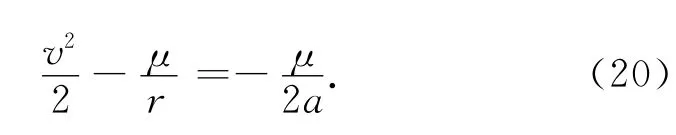
式中：v为探测器任一位置的速度大小；μ1为中心天体的引力常数；r为探测器至中心天体质心的距离。由此可得近木点处的速度

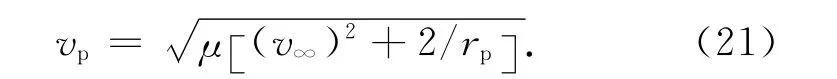
因此在近地点处的速度增量

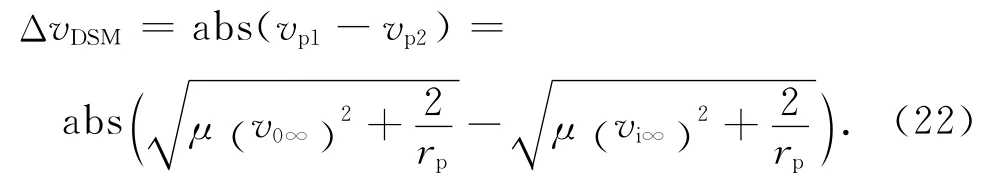
由此计算出了飞越时所需要的速度增量Δv以及近点地心距rp。用文献［4］中的方法可计算出瞄准的通径

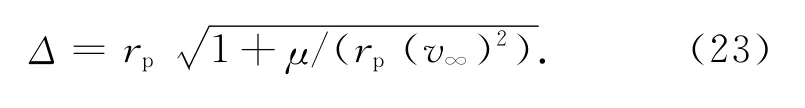
2.3 日心大倾角轨道设计方法

根据前文分析，在已知t0，tf时可设计出确定的星际转移轨道和木星借力轨道，并可据此计算该方案的包括地球逃逸C3能量、木星借力脉冲速度Δv、木星借力木心距rp、日心轨道半长轴、日心轨道倾角等指标。通过对设计指标的寻优，可完成日心大倾角轨道的优化设计。地球发射、木星借力至太阳极轨探测器轨道的初步设计方法如下：

a）初步确定发射日期、借力日期范围；

b）根据t0，tf，通过兰伯特问题求解得到地球逃逸速度增量Δvesp和木星进入时日心速度矢量vin；

c）根据i0，rp0，ra0，ω0，θ0的设计要求，由式（5）～（10）或式（11）～（14）计算vout；

d）由式（14）、（15）计算借力前后vrin，vrout；

e）根据vrin，vrout，用式（16）～（22）计算木星借力脉冲机动ΔvDSM和rp；

f）重复步骤b）～e），根据寻优算法优选转移方案。

3 仿真

尤利西斯探测器是美欧合作的太阳极轨探测器，于1990年10月6日11点47分由发现号航天飞机发射入轨，经16个月的地木转移后于1992年2月8日到达近木点，随后进入近日点1.34AU、远日点5.4AU、倾角80°的太阳极轨轨道。用本文方法分析尤利西斯探测器发射窗口，所得目标轨道倾角80°时发射－到达时间与近日点日心距rp0和地球逃逸C3的关系如图7所示。

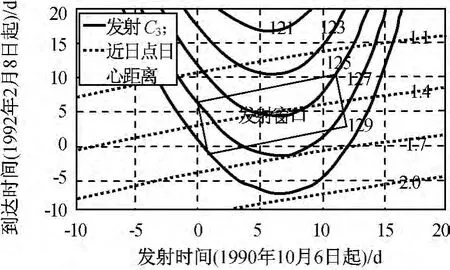
图7 发射－到达时间与近日点日心距和发射C3需求的关系（目标轨道倾角80°）Fig.7 Date of launch and arrival under launchC3and heliocentricrp

根据尤利西斯轨道设计要求，近日点距离范围应为1.28AU≤rp≤2.3AU，而探测器运载发射的C3最大能力为128.94km2／s2，得到发射窗口为发射时间1990年10月3日至1990年10月22日［5］。尤利西斯探测器实际发射日期为1990年10月6日，设计得到地木转移轨道和木星借力轨道参数见表3［5］。

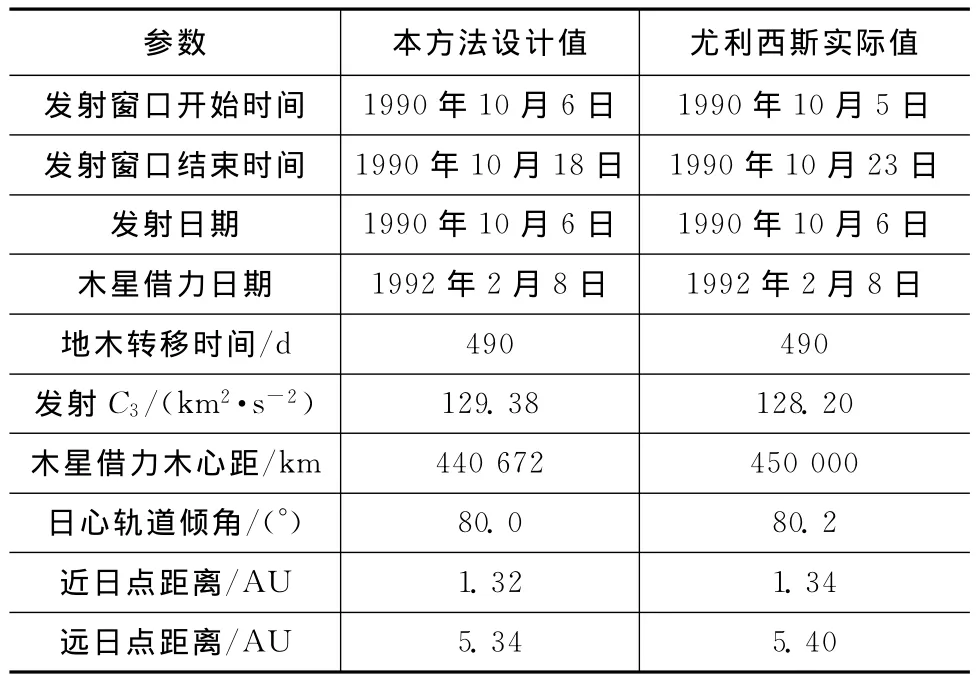
表3 尤利西斯探测器轨道设计结果Tab.3 Characteristics of Ulysses orbit designation

根据表3中的参数，设计1990年10月6日地球发射，1992年2月8日木星借力的太阳极轨探测器轨道如图8所示。可见本方法轨道设计结果与尤利西斯探测器轨道参数基本吻合，证明了本文方法在处理此类轨道设计问题中的有效性：在固定发射时间和到达时间时，发射所需C3和主要日心轨道参数误差为2%～3%，设计结果与尤利西斯轨道参数基本吻合。

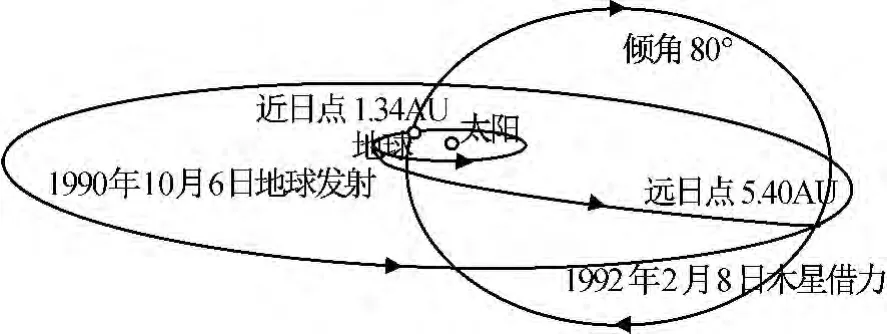
图8 尤利西斯探测器运行轨道Fig.8 Trajectory of Ulysses mission

4 结束语

本文对地球发射至太阳极轨探测器轨道设计方法进行了研究，分析了基于行星借力实现日心大倾角轨道的可行性，通过分析借力前后各轨道参数的关系给出借力参数计算方法并进行适当简化，给出太阳极轨的设计方法。用本文方法对尤利西斯探测器进行轨道设计，结果与实际轨道参数基本吻合，表明本文方法可用于此类轨道的初步设计。

［1］ 赵 钧.航天器轨道动力学［M］.哈尔滨：哈尔滨工业大学，2011.

［2］ CURTIS H D.轨道力学［M］.周建华，等（译）.北京：科学出版社，2009.

［3］ OLDENHUIS R P S.Trajectory optimization for a mission to the solar bow shock and minor planets［M］.Delft：Delft University of Technology，2010.

［4］ CAPDEROU M.Satellites orbits and missions［M］.Berlin：Springer，2005.

［5］ POJMAN J L.Ulysses：reference trajectory characteristics［R］.California Institute of Technology：JPL，1990.