密频结构实模态参数的特征曲线法

张 淼

在结构振动分析中，经常需要求解广义特征问题Kφ=λMφ，其中K和M是结构的质量和刚度矩阵，λ为特征值，φ为特征向量。求解特征值问题，即为求解结构的固有频率和振型，在工程实际应用及求解结构动力响应方面都具有重要的意义［1－2］。特征值即为结构的无阻尼固有频率(实频率)，特征向量即为结构的无阻尼固有振型(实模态)，再加上阻尼比，在工程中统称为实模态参数。一个结构的动力特性可以用它的实模态参数进行完整的描述，因此对它们的研究伴随着工程应用的设计、分析、修正、损伤识别等各个环节。若特征值和特征向量在设计参数的某可行域内或局部发生了转向和弯曲，表明结构对该设计参数是敏感的，尤需关注的是，结构很可能产生密频或重频现象［3］，从而为结构的稳定性带来隐患。特征对发生变化的测量方式之一是其导数，工程中称为灵敏度［4］，它们可在数值上反映变化的位置及弯曲发生的程度等。因此，特征曲线法的应用可以在很大程度上使设计工作远离可能产生危险的假定模型，在工程上具有良好的应用价值。

1 特征值分析

对N自由度的线性离散振动系统的运动方程为

式中M，C和K∈RN×N分别为系统的质量、阻尼和刚度矩阵。作拉普拉斯变换x(t)=uewt=ueiwt(w=iω)代入(1)式可得(w2Mu+wCu+Ku)ewt=0。令C=0，则无阻尼固有频率与规范化实模态为(ω2，φi)(i=1，2，…，N，w2=－ω2=λ)，满足特征方程

实际上特征方程(2)是关于矩阵M和K的广义特征问题。λi为固有频率(也可称为特征值)，φi为无阻尼正则实模态(也可称为特征向量)。

考虑如下弱耦合系统［5］，这是一个由两个弹性元件k1和k2及两个质量块m1和m2构成，并用一个弱弹性元件k联接的两自由度系统，假定只在x轴方向上发生振动，见图1。

图1 弱耦合系统示意图

特征方程

其中 p=m1m2，h=－(k1+k)m2－(k2+k)m1，c=k1k+k1k2+k2k.

令m1=m2=1，k2=1，而取设计参数为k1，其变化区间取为0.6至1.4，分别在k=0.05及k=0.01两种情况下用MATLAB绘制λ1和λ2关于设计参数k1的关系图(图2)。

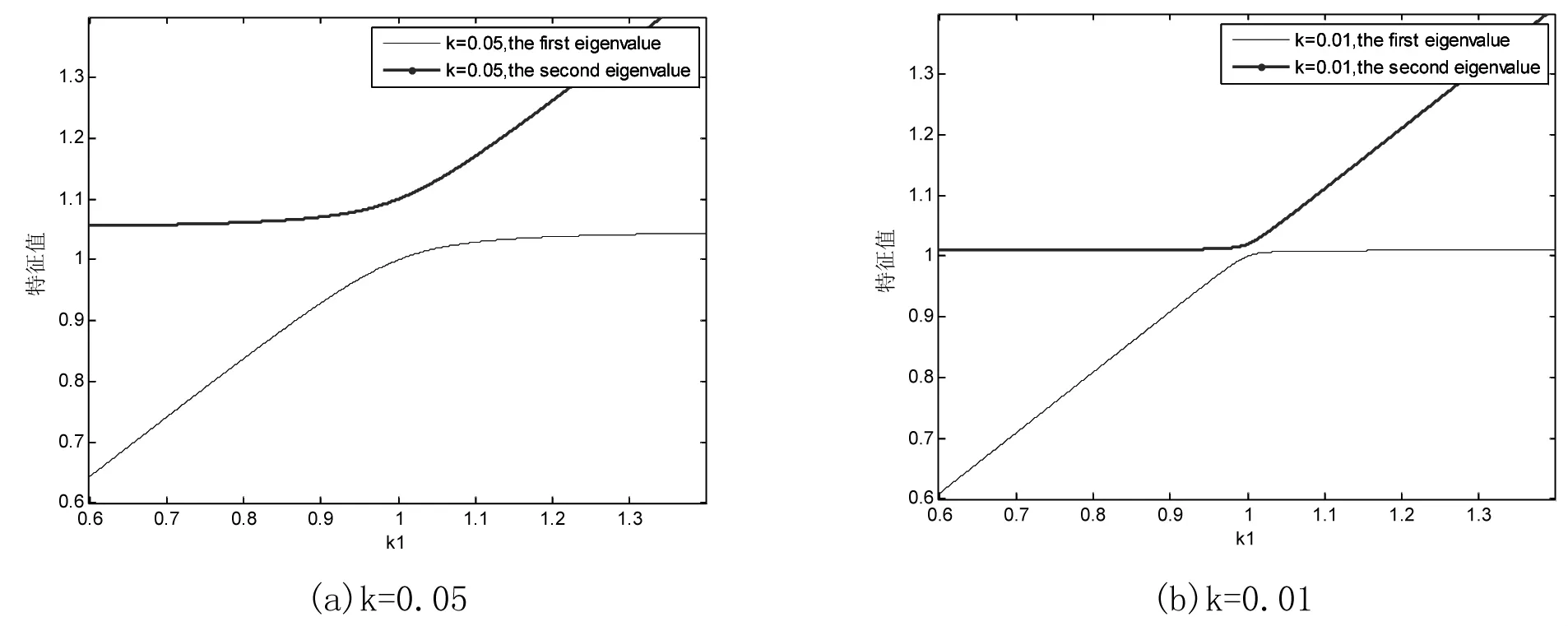
图2 特征值函数的关系图

由图2分析可知，首先对不同的k值，系统均在k1=1处发生两个特征值接近(密频)的现象，即在k1=1的邻域内出现了密频现象，而对k=0.01时更加接近一些，这说明更小的值会加重密频现象的发生。其次，两个特征值曲线均在k1=1处发生了弯曲与转向，k的取值越小，弯曲发生得越剧烈。

对公式(4)直接求导得两个特征值的一阶灵敏度为

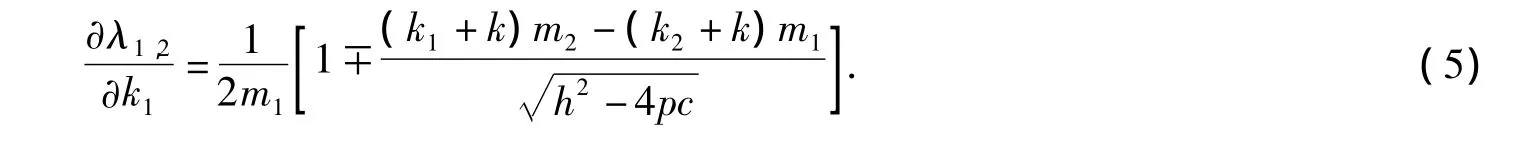
用MATLAB绘制λ1和λ2关于设计参数k1的一阶灵敏度关系图(图3)。

图3 特征值一阶灵敏度的关系图

由λ1的一阶灵敏度分析可知，在k1∈［0.6，0.9］内，λ1以几乎恒定的变化率增加;到k1=1附近时，变化率发生了较大变动，从1迅速地减少到0左右，其后不再发生大的变化，说明特征值λ1由与设计参数同步增加迅速地转变为与设计参数无关，只稳定在固定值。由λ2的一阶灵敏度分析可知，在k1∈［0.6，0.9］内，λ2变化率几乎为0，反映了λ2在此范围内不发生大的变化;到k1=1附近时变化率也发生了较大变动，从0迅速地增加到1左右，其后不再发生大的变动，说明λ2由稳定值迅速地转变为与设计参数的增加而同步增加。以上说明，两条特征值曲线均在k1∈［0.9，1.1］范围附近发生了剧烈的转向和弯曲，而且k的取值越小，弯曲发生得越剧烈。这一分析与图2的分析结果一致，可见灵敏度分析确实能反映系统的原始动特性。

2 特征向量分析

相应地，规范化特征向量为

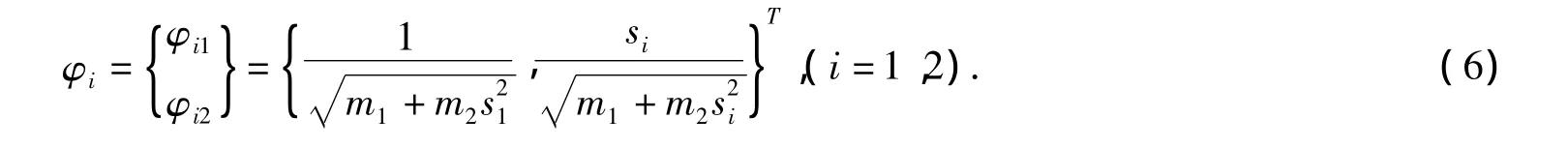
用MATLAB绘制φ1和φ2关于设计参数k1的关系，见图4和图5。

图4 φ1关于设计参数k1的关系图

图5 φ2关于设计参数k1的关系图

对不同的k值，模态1的第1维分量与第2维分量均在k1=1附近发生了转向，且变化剧烈。在k1=1的小幅变化范围内，k的取值越小，模态1所发生的变化越剧烈。这说明模态1的不稳定性发生在密频点k1=1处。同样地，对不同的k值，模态2的第1维分量与第2维分量均在k1=1附近发生了转向，且变化剧烈。模态的不稳定性也发生在密频点k1=1处。从前文的分析可知，由于k取值越小，显示结构密频的程度越高，因此图4和图5反映的是密频的程度越高，模态的跳跃性越强。

用公式(6)式直接求导得两个特征向量的一阶灵敏度为

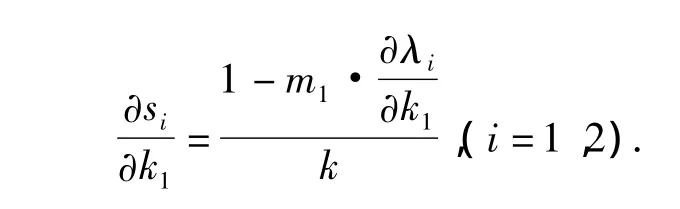
用MATLAB绘制φ1和φ2的第1维分量关于设计参数k1的一阶灵敏度关系见图6。

图6 不同k值时φ1和φ2的第1维分量关于设计参数k1的一阶灵敏度对比图

图6仅以模态1和模态2的第1维分量为研究对象，图形显示，这两个模态的第1维分量均在k1∈［0.6，0.9］范围左右变化率几乎为0，说明模态此时随设计参数的变化不大，较为稳定;但在k1∈［0.9，1.1］范围附近，变化率发生了较大的变动，其中k值越小，变化率变化的幅度越大，显示出模态在这个范围内发生了一定程度的跳跃;然后变化率又几乎为0，模态又呈现出稳定状态。这一分析结果与图4和图5的分析结果一致。

3 结语

本文针对一个弱耦合系统，首先利用特征值及特征向量与设计参数的关系图，来分析设计参数对系统状态的影响，尤其是发生密频现象时，密频现象对结构可能产生的破坏作用进行了分析;再利用特征值与特征向量关于设计参数的灵敏度曲线图，来分析和验证上述结果，表明特征对灵敏度分析确实能在很大程度上反映结构性态。同时说明在工程实践中若没有条件获得足够的结构原始实模态参数信息，却仅凭其导数信息，也可判断和预知那些隐藏的信息，在一定程度上能够节省研究和设计的成本。

［1］张淼，鞠伟.计算各种振系模态灵敏度的统一算法［J］.长春工程学院学报:自然科学版，2012，13(4):119－122.

［2］于澜.模态参数的灵敏度分析在结构工程领域中的应用［J］.长春工程学院学报:自然科学版，2012，13(3):1－3.

［3］张淼.基于松驰技术的重频密频结构模态灵敏度分析［J］.合肥工业大学学报:自然科学版，2012，35(12):1605－1609.

［4］于澜，张淼，鞠伟，等.非保守系统复模态的规范正交性及其应用［J］.华南师范大学学报:自然科学版，2013，45(4):21－24.

［5］于澜，张文丹，付向南.非对称重频阻尼系统状态向量的摄动分析［J］.长春理工大学学报:自然科学版，2011，34(3):170－172.