无急回特性曲柄摇杆机构的优化设计

苏有良

曲柄摇杆机构的设计可采用图解法，也可采用解析法进行设计.图解法设计精度低，解析法计算繁杂［1］.在设计无急回特性摇杆机构时，我们希望所设计的机构具有较优传动性能和合理结构尺寸，同时使设计计算过程变得简单，并达到设计结果精度高的目的.为了实现这一目的，本文通过分析推导得到γmin1=γmin2(如图2，γmin1是曲柄与机架重合共线位置时机构的传动角，γmin2是曲柄与机架拉直共线位置时机构的传动角);通过分析建立了曲柄摇杆机构的设计公式，公式中当给定摇杆摆角和d/c时，即可求出a/c、b/c的比值，显然当初定某杆长度就可根据d/c、a/c、b/c的比值求出其余各杆长度;同时建立了最小传动角与杆比的函数方程，并依据函数方程应用MATLAB编写程序获得γmin－d/c变化线图，通过γmin1－d/c变化线图取合适的d/c值就可使所设计的机构具有较优传动性能和合理结构尺寸.按d/c的取值和给定的摆角以及初定的某杆长度时，根据设计计算公式就可方便地计算出其余各杆长度.通过此法不仅使所设计的无急回特性曲柄摇杆机构具有较优传动性能和合理结构尺寸，而且使设计过程变得简单灵活、精度高.

1 无急回特性曲柄摇杆机构杆长与机架要求及的分析

图1中，AB为主动曲柄，令 AB=a、BC=b、CD=c、AD=d，φ 为摇杆的摆角、θ为极位夹角.

图1 曲柄摇杆机构处两极限位置简图

图2 具有最小传动角所处两位置简图

在图1中，由三角形AC1D和AC2D得:

若 θ=00，则 A、B1、C1、B2、C2各点共线.由此可得:

将(1)减(2)可得:

将(4)和(5)联立，同时因传动角为锐角，所以无急回特性曲柄摇杆机构所处两位置最小传动角γmin1和γmin2的关系是 γmin1=γmin2=γmin.

2 无急回特性曲柄摇杆机构设计方程

由图1三角形AC1C2得:

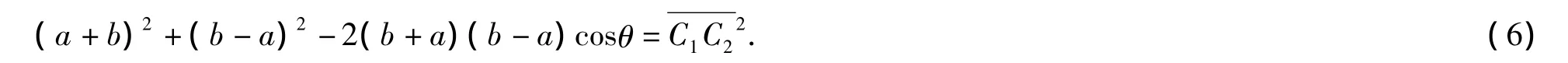
将(3)代入(1)或(2)可得:

(4)式中，a是曲柄的长度，a必最小;d是机架的长度，d必最长［2］.故无急回特性曲柄摇杆机构的存在要求是［3］:最短杆与最长杆的平方和=其余两杆平方和;机架为最长杆.

在图2中，∠B2C2D=γmin1和180°－∠B1C1D=γmin2两角之一为机构的最小传动角［4］，

由△B2C2D和△B1C1D得:

令图1中摆角∠C1DC2=ψ，由三角形DC1C2得:

当 θ=0°时，将(5)和(6)联立得:

由图2中的三角形B2C2D(γmin1=γmin2=γmin)得:

将a2+d2=c2+b2代入(9)得:

由(10)式可得:

由(4)式可得:

综上分析结果，无急回特性曲柄摇杆机构的设计计算公式为:

当无急回特性曲柄摇杆机构给定摇杆摆角和d/c时，根据(13)即可求出a/c、b/c的比值，显然当初定某杆长度就可根据d/c、a/c、b/c的比值求出其余各杆长度.

3 最小传动角γmin随杆比d/c变化情况分析

将(8)分别代入(11)、(12)分别可得(14)和(15):

将(14)和(15)联立可得(x=d/c):

由(16)可得:

根据上式，利用MATLAB编写程序并运行，可得:

输入 fplot(f1，［1，10］)［5］，得到图 3.

图3 γmin－d/c变化线图(ψ=80°)

图4 γmin－d/c变化线图(ψ=90°)

同理，若当ψ=90°时，根据(17)应用MATLAB编写程序运行后可得图4.

从图3并结合所编程序运行的结果可以看出，当摆角ψ一定时，最小传动角γmin随机架与连杆长度比d/c的增大而增大.当d/c=1时，γmin=0;当d/c=9.9999时，γmin=0.8702rad;当d/c=1～2时，最小传动角γmin随d/c的增大而急剧增大;d/c=2～3时，最小传动角γmin随d/c的增大而缓慢增加;d/c＞3时，d/c增大很多时，最小传动角γmin也只会有很小的增加，显然此时的机构结构尺寸增加较大.所以当d/c的值取在2附近时，此时机构有较好的传动性能和较为合适的结构尺寸(图4分析同图3分析).

4 应用实例

例 设计无急回特性曲柄摇杆机构，已知摆角ψ=80°，摆杆c=10.00cm.要求设计结果结构尺寸合理、传动性能较优.

解 按图3，γmin－d/c变化线图分析，取d/c=2.0，γmin=0.8012rad=45.93°，此时的无急回特性曲柄摇杆机构结构尺寸合理、传动性能较优.

将d/c=2.0，代入(13)可得:

将摆杆c=10.00cm代入上式，则所得设计结果为:

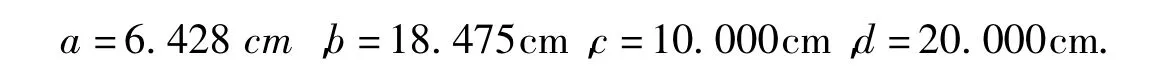
将设计结果代入(4)可得b2+c2=a2+d2=441.3.可知，设计结果满足无急回特性曲柄摇杆机构的杆长条件.此时以d杆为机架就可得到满足设计条件要求的无急回特性曲柄摇杆机构.

5 结语

综上所述，通过分析建立最小传动角与杆比的函数方程，依据所建立的函数方程应用MATLAB编写程序获得γmin－d/c变化线图，通过γmin－d/c变化线图可分析无急回特性曲柄摇杆机构传动性能随d/c变化情况，此时根据γmin－d/c变化线图所取的d/c的值可使机构具有较优传动性能和合理结构尺寸.按d/c的取值和给定的摆角，根据设计方程就可计算出摆杆与其余各杆比值，当初定某杆长度时就可方便地计算出其余各杆长度.通过此法不仅使所设计的无急回特性曲柄摇杆机构具有较优传动性能和合理结构尺寸，而且使设计过程变得简单灵活、精度高.

［1］梁崇高.平面连杆机构的计算设计［M］.北京:高等教育出版社，1993.

［2］郑文伟，吴克坚.机械原理［M］.7版.北京:高等教育出版社，1997:96－103.

［3］苏有良.无急回特性曲柄摇杆机构解析设计法［J］.轻工机械，2007(1):60－62.

［4］孙恒，陈作模.机械原理［M］.北京:高等教育出版社，1996:180.

［5］苏有良.偏置摆动导杆机构的解析设计与运动仿真［J］.机械设计，2013(10):21－24.