局部阴影条件下光伏阵列的建模与优化设计

张玉发

(中电电气〈南京〉太阳能研究院有限公司，江苏 南京211106)

0 引言

太阳能作为一种新型的绿色可再生能源，具有永不枯竭、不受地域限制、清洁环保等优点，正被迅速推广应用。为保证发电效率，在光伏发电系统阵列设计和安装时常遵循以下原则：光伏阵列东、西、南一定范围内没有高大的建筑物、树木等遮挡物。然而在工程实际中，由于城市密集的高大建筑物、树木甚至云层遮挡、阵列表面的灰尘、树叶等因素，使阵列不可避免地产生阴影或受光不匀等问题。此时组件的输出伏安特性曲即为台阶状，对应的功率电压曲线显现多峰值。现有的数学模型只能描述太阳能光伏阵列在日照均匀的条件下的特性，并不适用于光照不均匀情况下光伏阵列的研究。因此，创建局部阴影条件下的数学模型并对分析其输出特性，从而优化光伏系统的阵列设计，具有十分重要的现实意义。

根据光伏电池的工程应用模型，结合串并联电路的原理，建立了光伏阵列在局部阴影条件下的数学模型，研究光伏阵列在局部遮挡情况下的输出特性与阴影数量、阵列格局、遮挡模式等因素的关系，并根据阵列输出特性随阵列的布局、阴影的数量和分布以及遮挡模式的不同而有所差异，给出光伏阵列优化设计方法，为光伏发电系统的工程优化设计提供依据。

1 局部遮挡条件下光伏阵列的建模

在实际应用中，光伏组件制造商通常只向用户提供产品在标准试验条件(standard test condition，STC)下测出的短路电流Isc、开路电压Voc、最大功率点电流Im和最大功率点电压Vm值。本文选择文献[2]提供的光伏电池工程用数学模型：

其中：

在光照强度不超过2个太阳常数时，式(1)误差较小[2]。

光伏阵列是由若干光伏组件根据逆变器电气特性要求，通过串并联的方式组成的较大功率的装置。因此，光伏阵列和单个组件之间有如下关系：

式中：V、I、P为单个光伏组件的输出电压、输出电流、输出功率；Ns、Np为光伏组件串联数目和并联数目，若Nt为光伏阵列总的组件数，则Nt=NsNp；Va、Ia、Pa光伏阵列的输出电压、输出电流、输出功率。

因此，可以用如下方程描述同一光照下光伏阵列的数学模型：

式中Ia是阵列电流，Va是阵列电压。但是当光伏阵列工作于局部阴影条件时，式(7)不再适用。为便于建立局部阴影条件下光伏阵列的数学模型，约定相关术语如下：

将具有相同光照和温度的单串阵列中的组件称为子串，如图1(b)中的Ns1；

将具有相同阴影条件的单串阵列并联在一起称之为子阵列Group（简称Gx），见图1(c)。

建立只有2个子串串联的单串阵列为单元的光伏阵列的数学模型。正常光照的子串称为Ns1，局部阴影的子串称为Ns2，在非均匀光照强度下，子串Ns1产生的电流Isc1大于Ns2产生的电流Isc2，即Isc1ffgt;Isc2。

图1光伏阵列模型示意图

当确定了温度、光照和阵列布局时，负载阻抗决定了光伏阵列工作在其特性曲线什么位置。 当电路负荷较大时，组件将工作在小电流条件下，若组件的电流不大于Ns2产生的光电流，这时Ns2最大功率点即为局部阴影组件的最大功率点。随着电路负荷的减少，组件的电流逐渐加大，当组件电流大于Ns2产生的光电流时，配置于Ns2侧的旁路二极管导通，对其形成反向电压，Ns2及旁路二极管成为Ns1的负载。此时Ns1的最大功率点即为局部阴影组件的最大功率点。

综上所述，得出由2个子串串联组成的单串阵列特性方程的分段函数：

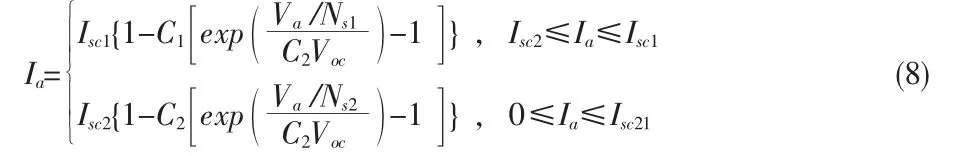
因此，由式(4)—(6)和式(8)得出图1(d)所示光伏阵列在任意阴影情况下的数学模型：

式中Ix、Vx为式(8)提供的单串阵列模型的电流及电压。

为了验证上述模型，对2块组件串联组成的单串阵列进行模拟仿真并与测试值进行比较。实验采用BP太阳能生产的BP585U光伏组件。其标称参数为：Pmax=85W，Voc=22.1V，Isc=5A，Vm=18V，Im=4.72A。参考温度是25℃，参考光照为1000W/m2。遮挡部分光照为166W/m2。根据式(8)画出模型的I-V、P-V曲线，与实测的曲线相比较见图2。

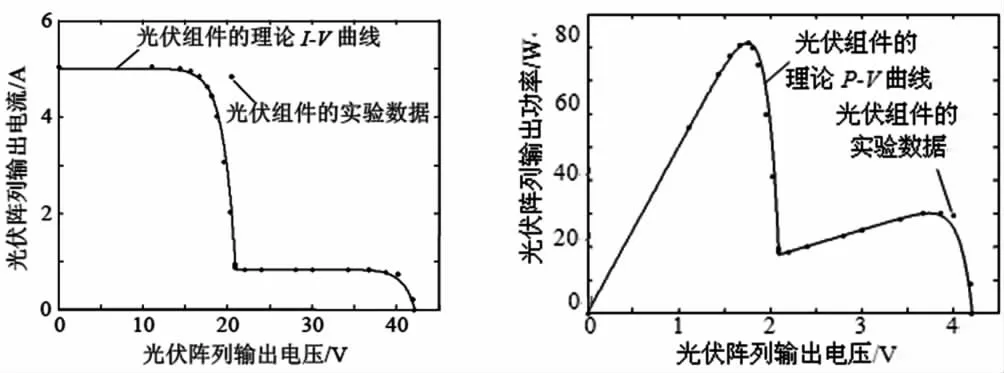
图2 2串联组件阴影条件下的实验与理论输出特性曲线

从图2可以看出理论值和实验值略有不同，是因为仿真模型忽略了二极管的损耗以及组件串联匹配因素，但误差在可接受的精度范围，因此可用式(8)描述2个子串串联的单串阵列。光伏阵列的建模是以式(8)为基础的，因此式(9)也可以准确地描述光伏阵列在任意阴影条件下的输出特性。

2 局部阴影对阵列输出特性的分析

通常光伏电站阵列大小由光伏系统安装容量和光伏组件的额定功率决定，光伏组件的串联数则由光伏供电系统的额定电压和光伏组件的最佳工作电压决定。例如，采用额定功率和最佳工作电压分别为125W和35V的光伏组件组成一个功率为4.5kW的系统。如果用于光伏扬水，阵列可采用{12×3}的结构，通过逆变器直接驱动三相380V的水泵电机，无需升压；如果用于单相并网发电，考虑到逆变器的升压电路的作用，阵列可采用{6×6}结构。

为分析阴影对阵列输出特性曲线的影响，引入透光因子的概念：

式中：Es为有阴影电池板的光照强度；Eref为参考光照强度，通常取1000W/m2。

假定阴影数量不超过光伏阵列组件总数的1/3，r=0.4。用式(9)对不同的阴影数量及可能的阴影分布模型进行仿真计算，得出所对应的最优及最差阴影分布。在本小节的讨论中，假定每块光伏组件均配备旁路二极管，防止热斑效应的产生；每个组串串接一个防反二极管，防止并联运行时逆电流的通过。

对于{12×3}阵列，若阴影数为6，则相应的阴影分布和输出功率如表1所示。

表1局部阴影条件下最大功率点

由表1可以看出，不同阴影分布对阵列输出功率影响差异很大。最优阴影分布为[2:2:2]，对应的输出功率为3.95kW；最差阴影分布为[5:1:0]，对应的输出功率为3.54kW。最优与最差阴影分布情况相差0.41kW，占最大功率的10.4%。随着阴影数量的增加，最优分布与最差分布的偏差呈上升趋势。表2和表3列出了{12×3}、{6×6}阵列的最优分布与最差分布时最大输出功率值以及两者之间的偏差。

表2{12×3}阵列局部阴影条件下的最佳分布及最差分布

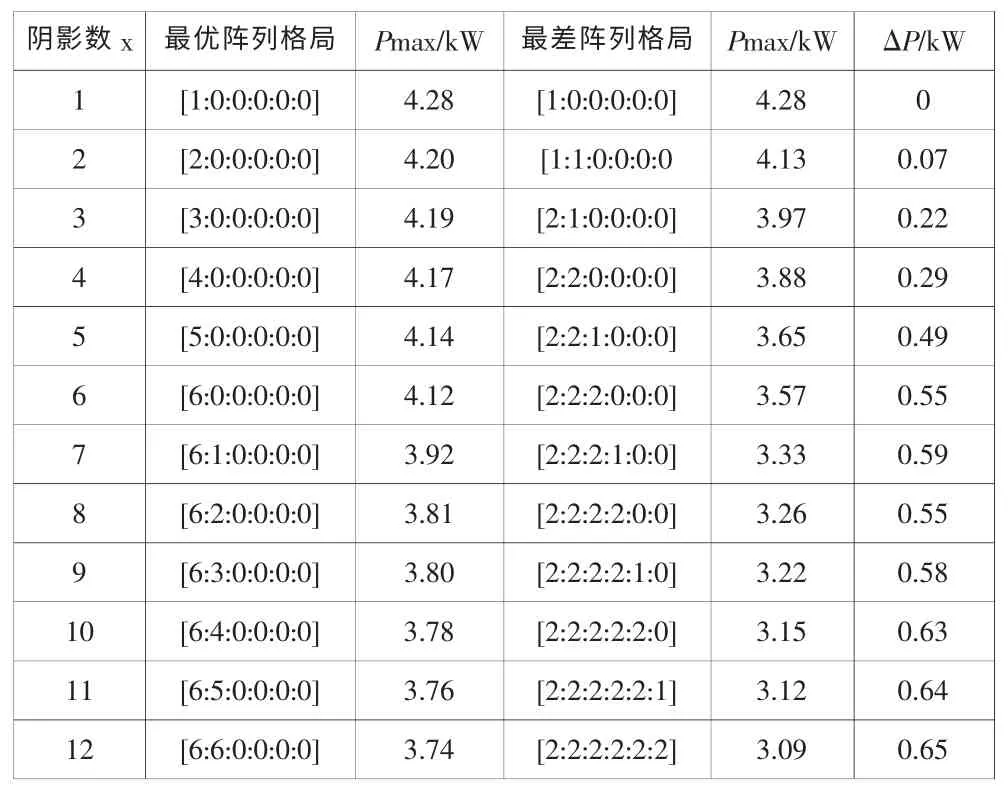
表3{6×6}局部阴影条件下最优分布及最差分布

由表2和表3的数据得出：

1）阴影对阵列的输出功率影响很大。阴影越多，功率损失越大。但是最大输出功率损失与阴影数量不成线性比例关系。

2）不同的阴影分布对阵列最大输出功率的影响很大。阴影越多，最优分布与最差分布所能获得的最大输出功率的偏差越明显，甚至高达20.7%。因此，阴影分布的优化设计是十分必要的。

3）阵列的输出特性受不同阵列布局的影响呈现不同的特性，因而最优阴影分布的特点也不同。对于串联数多，并联数少的阵列，例如{12×3}阵列，阴影总数远离串联组件总数时，通常阴影均匀地分布于各串阵列中能获得较大的输出功率，如表2所列；阴影总数接近串联组件总数时，通常阴影集中在某(几)个串联阵列中能获得较大的输出功率。串联数少，并联数多的阵列，例如{6×6}阵列，阴影集中分布能获得较大的输出功率，如表3所列。

除了阴影分布和阵列格局，遮挡模式、温度、光照等也会使光伏阵列的输出特性曲线发生变化。当单串阵列存在遮挡的时候，不同遮挡模式对应的光伏阵列输出不同的特性曲线，具体伏安特性曲线会呈现多个阶梯形，功率电压曲线呈现局域多峰状。由此可以推论出在单串阵列受到M个不同强度的光照射时，阵列的I-V特性曲线将出现M个膝型平台，P-V特性曲线将出现M个峰值。

此时若用传统的MPPT方法会使光伏系统工作在某一个较小的峰值附近，而错过了真正的最大功率点。

3 光伏阵列的优化设计

基于局部阴影下光伏阵列的数学模型的建立，理论计算及实测数据分析，总结出光伏阵列优化设计的基本原则如下：

1）根据实际的安装条件，实测量和利用软件仿真，确定发生阴影的时间段、阴影数及透光因子，在保证满足系统工作电压的前提下，调整阵列串并联数，尽量使阴影数为串联数或并联数的整数倍；

2）如系统结构简单，可直接选择在各串阵列中均匀分布或集中分布阴影；

3）在不同的季节、不同的时间段，遮挡的阴影数量及影响会发生变化。当选择的逆变器输入工作电压（MPPT）范围宽时，可使阵列的阴影分布均匀，以获取系统最大的输出；当选择的逆变器工作电压（MPPT）范围窄时，为了使不致使系统因欠压而保护，保证逆变器正常工作，通常电气连接时使阴影集中分布于某一串中，同时保证系统最大的输出；

4）根据以上设计原则，可以将光伏系统优化设计按照如图流程进行（图3）。

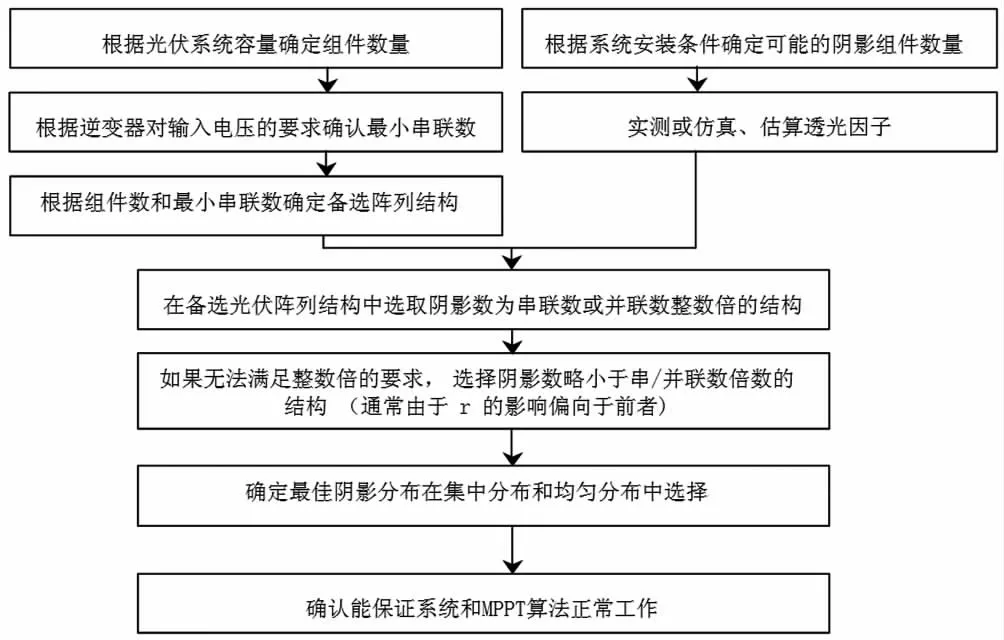
图3光伏阵列优化设计流程图

4 结论

本文以光伏电池的工程模型为基础，结合串并联电路理论，建立了局部阴影条件下光伏阵列的数学模型，并进行了详细的理论分析和实验验证，验证了局部阴影条件下光伏阵列的输出特性可以用分段函数较准确的描述，而且该特性除了与常规的温度、光照等因素有关，与阴影数量、阵列布局、遮挡模式也息息相关。通过分析和实测，提出了阵列优化设计是将阴影以集中式分布于单串阵列或均匀分布于各串阵列的特点，并且阴影集中于组串阵列分布时最大功率点电压最高，不影响系统MPPT正常运行。总结了针对阴影影响光伏系统设计的优化原则，给出了系统优化设计流程，为工程实际应用提供了可靠的支持。

［1］峁美琴，余世杰，苏建徽.带MPPT功能的光伏阵列matlab通用仿真模型[J].系统仿真学报，2005，17（5）：1248-1251.

［2］苏建徽，余世杰，赵为，等.硅太阳电池工程用数学模型[J].太阳能学报，2005，20（5）：409-412.

［3］肖景良，徐政，林崇，等.局部阴影条件下光伏阵列的优化设计[J].中国电机工程学报，2009，29（11）：119-124.

［4］翟载腾，程晓舫，丁金磊，等.被部分遮挡的串联光伏组件输出特性[J].中国科学技术大学学报，2009，39（4）：398-402.

［5］陈如亮.光伏热斑现象及多峰最大功率跟踪的研究[D].汕头：汕头大学，2007.

［6］翟载腾.任意条件下光伏阵列的输出性能预测[D].合肥：中国科学技术大学，2008.

［7］刘素梅.光伏方阵失配现象研究[D].汕头：汕头大学，2008.

［8］王章权，张超，何湘宁.基于Pspice模拟行为模型的光伏阵列建模[J].计算机仿真，2007，24（8）：225-240.

［9］刘晓艳，祁新梅，等，电网技术，局部阴影条件下光伏阵列的建模与分析.2010，11，34（11）：192-197.