浅谈不定式极限

张石凤

（云南大学旅游文化学院 信息科学与技术系，云南 丽江674100）

limα(x)=limβ(x)=0.

对于这种类型的未定式是非常重要的一种极限，求该类型的极限，通常用到洛必达法则。

定理1.1（洛必达法则） 若函数α(x)与β(x)满足条件：

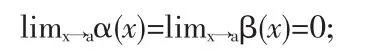
(2)在点 a的某去心领域内 α(x)与 β(x)可导，且 β'(x)≠0；

(3)limx→a存在（或为∞）

则 limx→a=limx→a

注：（1） 极限过程改为 x→a+,x→a-,x→∞,x→-∞,x→+∞ 有类似的结论。

（2）若 limx→a仍然满足洛必达法则的条件，则可连续运用该法则，即:limx→a=limx→a

（3）若 limx→a不存在（不含∞）,不能断言limx→a不存在。

在实际计算中，常常把该法则与等价变形、重要极限及等价无穷小代换等其他求极限的重要方法一起使用。

解：若用洛必达法则，分子分母分别求导得limx→0，该极限为振荡不存在，故洛必达法则失效。实际上，可利用等价无穷小量代换 ln（1+x）∽x（x→0），得

limα(x)=limβ(x)=∞

定理2.1（洛必达法则） 若函数α(x)与β(x)满足条件：

（1）limx→aα(x)=limx→aβ(x)=∞；

（2）在点 a 的某去心领域内 α(x)与 β(x)可导，且 β'(x)≠0；

（3）limx→a存在（或为 ∞）

则 limx→a=limx→a

该定理也有类似于定理1.1的注释，定理1.1与定理1.2统称为洛必达法则。

3 其它类型的不定式极限

不定式极限还有0·∞，∞-∞，1∞，∞0等类型。经过简单变换，它们一般都可化为型或型的极限。

对于0·∞及∞-∞型不定式极限，经过适当的变化，即可将其化为型或的极限。

例 4 limx→0＋x ln x（0·∞）

对于该种类型的不定式极限，只要将其一除至分母，即可将其化为型或的极限。

对1∞，00，∞0等型不定式极限，可先化为以e为底的指数函数的极限，再利用指数函数的连续性，化为求指数部分的极限，而指数部分的极限，可化为型或的极限，再运用洛必达法则即可。

例 7 limx→0+χx（00）

解：limx→0+

χx=limx→0+eχlnx=e0=1.

4 总结

洛必达法则是解决不定式极限的很有效的方法。但必须注意的是，只有型和型不定式而且必须在符合洛必达法则的各项条件时才能直接使用洛必达法则。对于其他型不定式必须经过变换化为满足条件的型和型不定式才能使用洛必达法则。有时还需要与其他求极限的方法结合使用。在求极限时，不必一一去验证洛必达法则的各项条件，只要判断是型和型不定式即可先用着洛必达法则，若求极限过程可进行下去，说明洛必达法则可以失效，若运用洛必达法则不能得出最后结果（极限不存在），这个时候说明洛必达法则失效，不能使用，不能说明该极限不存在，此时需要用别的办法判断极限是否存在。

［1］赵树嫄．经济应用数学基础（一）微积分[M].3版.中国人民大学出版社.

［2］华东师范大学数学系编.数学分析:上册[M].3版.高等教育出版社.