破解实质蕴涵怪论之谜
●李铁强
(武警学院部队管理系,河北廊坊 065000)
(本栏责任编辑、校对 李献惠)
在经典命题演算系统中,出现了四个让人费解的实质蕴涵怪论:(1)p→(q→p)。即真命题被任何命题所蕴涵。(2)~p→(p→q)。即假命题蕴涵任何命题。(3)(p→q)∨(q→p)。即任一两个命题之间都有蕴涵关系。(4)(p→q)∨(p→~q)。即任意命题p不是蕴涵任意命题q,就是蕴涵~q。
对于为什么会出现这些怪论又如何消除它们,是逻辑学研究的一项重要任务。要完成这一任务,我们必须仔细审视如下对于实质蕴涵理论一般性评价的真实性:“实质蕴涵抽象、概括出了语言中‘如果,则’这类联结词的共性,在对‘如果,则’的各种解释中是最弱的,因而具有普遍适用性和简单性,而这种普适性和简单性是逻辑的本质要求”[1],并由此出发,探讨消除实质蕴涵怪论的途径。
一、实质蕴涵经典含义的内在矛盾性
把真值和真值函项的概念引入逻辑,是现代命题逻辑取得实质性进步的关键环节。但是,在用“→”来表示的实质蕴涵以概括性地把握“如果…那么…”的条件句时,“p→q”的真值与“如果p那么q”这种形式的条件句的真假是否是一致的?
如果我们把讨论问题的范围限定在原子命题的范围之内,那么非常明显的是,命题p的真值与命题p的真假是完全一致的。但是,如果我们把讨论问题的范围限定在除了~p之外的复合命题的范围之内,那么情况就会变得复杂起来。事实上,自古希腊提出蕴涵概念开始,将“如果p那么q”的真假与“p→q”的真值就混淆起来。我们以实质蕴涵的首倡者斐洛为例。他认为“一个条件命题是正确的,不是前件真,后件假。”这就是说,一个真的充分条件假言命题可以用三种方式得到:(1)以真的前件开始并且以真的后件结束。例如:“如果这是白天,那么这是亮的。”(2)以假的前件开始并且以假的后件结束。例如:“如果地球会飞,那么地球有翼。”(3)以假的前件开始以真的后件结束。例如:“如果地球会飞,那么地球存在。另外当且仅当前件真而后件假时,条件命题才是假的。例如:“如果是白天,那么是黑夜。”[2]从斐洛对蕴涵命题的定义和他举例的方式来看,他的核心思想是,条件命题的真值与条件命题的真假是完全一致的。这种思想深刻地影响了从皮尔士、弗雷泽,到罗素、维特根斯坦等众多的现代逻辑学家,使他们普遍继承并坚持这一观点,所以,他们才丝毫不怀疑斐洛所例示的条件命题的真实性,进而构造出不计其数且认为是正确的类似命题。此种对条件命题的理解所导致的最为致命的后果是,一个条件命题的真假可以由前件和后件的一组真值来确定。[3]而这一点却给条件命题的描述引入不可避免的矛盾:用前件和后件的一组赋值的真正目的是确定条件命题的真假。但如果是这样的话,我们将无法确定一个条件命题的真假。以“如果两物体产生摩擦,那么地面会湿”这个命题为例,在某种场景之下,前件和后件都是真,依据斐洛的观点,这个条件命题是真的;但是,这个命题在另外的场景之下,会出现前件真而后件假的情形,这样依据斐洛的观点,这个条件命题是假的。所以,如果斐洛的观点是正确的话,那么我们不得不得出这样的结论,条件命题的真假因时而异、因地而异!
这样的结论与我们通常要建立“如果p那么q”形式的条件命题、特别是用这种形式建立科学理论的目的是背道而驰的。建立条件命题的目的是要寻求前件和后件之间的必然联系,通过利用这种联系,我们可以有效地预期未来或者对事物的运动变化和发展实施有效的控制,以达到认识世界和改造世界的目的。在通常情况下,条件命题,如“如果两物体产生摩擦,那么会产生热”,并不对前件和后件的真假做出具体的承诺,它只是承诺:当两物体确实产生摩擦时,一定会产生热;当两物体没有产生摩擦时,它可能会产生热也可能不产生热;不会发生这样的情况,当两物体产生摩擦时,没有热量产生。这样的承诺与墨子学派的经典描述:“有之必然,无之未必不然”完全吻合,而与实质蕴涵的经典描述不完全相符。
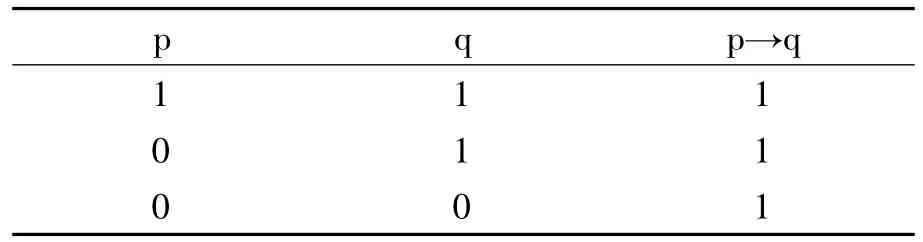
国内普通逻辑教材中充分条件假言命题的定义,由于采用墨家学派的经典描述,因而与科学中条件命题的使用相符合;它把充分条件假言命题之真与真值在不自觉间有效区分开来,即前件和后件的一组确定真值赋值不足以确定充分条件命题的真假,其真必须在综合地考察前件和后件的全部赋值对后才能确定:它既要考察前件p与后件q在不同的情形下是否会出现赋值对〈1,1〉与〈1,0〉以确定是否满足“有之必然”,也要考察在不同的情况下是否会出现〈0,1〉与〈0,0〉以确定是否满足“无之未必不然”。当然作为逻辑的抽象,当我们用符号表示充分条件假言命题的变项和常项后,一个真的充分条件假言命题的真值情况就可以用真值表(如下)来表示。这个真值表的地位极其重要。因为就是依据这个真值表我们才得到充分条件假言命题推理的基本规则和两个基本推理有效形式:肯定前件式和否定后件式。在此我们应特别注意其基本有效式的建立过程(以肯定前件式为例):假定“如果p那么q”是真的,p和 q的真值有三种可能:〈1,1〉、〈0,1〉和〈0,0〉,这清楚地表明,一个真充分条件假言命题是不能断定前件与后件具体真值情况的;当第二个前提断定了前件真的情况下,我们才从这三行真值中断定,只有第一行才满足“如果p那么q”和p都是真,所以,q必真。
p q p→q 1 1 1 0 1 1 0 0 1
既然在建立基本有效推理式的时候,从假定“如果p那么q”是真的不能具体断定前件和后件的真值,那么我们有什么样的理由在知道前件和后件的一组真值组合后就断定“如果p那么q”是真或假的呢?即使在这种情况下我们有充分的理由断定“如果p那么q”的真值,但有什么确切的理由说其真值与其真假是一致的呢?实质蕴涵理论恰恰做出了这样的断定。这种把真值与真假视为等同的观点导致了实质蕴涵的内在矛盾性:一方面,当这种理论建立基本推理有效式时默认了前面的真值表,即从“p→q”是真的出发,只能陈列p和q的各种可能的真值组合,而不能具体断定前件和后件的真值;但另一方面,当p和q的某种真值组合确立后,这种理论却不仅立即断定“p→q”的真值,也同时断定了“p→q”的真假,并以此为依据构造出众多的与人们的直观相违背的条件命题。
二、产生实质蕴涵怪论的原因
当逻辑学家用真值函项理论刻画实质蕴涵以及整个命题逻辑时,他们都没有真诚地、科学地对待真值函项这个概念,进而导致实质蕴涵的内在矛盾性;这种矛盾性的进一步后果是实质蕴涵的多样化,而这一点正是产生实质蕴涵怪论的原因。
既然实质蕴涵理论是用函数理论来刻画的,那么,用函数做类比既是恰当的也是有益的。我们的问题是:在什么情况下,函数f(x)和g(x)两者相等;又在什么情况下它们不相等呢?用标准的数学语言来说其答案非常简单:f(x)=g(x),当且仅当对于x的任意赋值 xi,f(xi)=g(xi);f(x)≠g(x),当且仅当存在着赋值xi,使得f(xi)≠g(xi),而不管有多少情况xj,使f(xj)=g(xj)。数学家乃至学习函数的学生,从来没有把一个点或几个点看作曲线或曲面,因为有无数条曲线或曲面会通过一个或几个点,但当经典实质蕴涵理论把复合命题的真值充当其真假时,恰恰是用一个或几个点来代替曲线或曲面。于是,多种实质蕴涵就出现了。
当且仅当p与q的真值组合至少有一种不可能实现时,这种情况下的实质蕴涵“p→q”是限定赋值实质蕴涵。事实上,日本学者石黑满虽然没有提出限定赋值实质蕴涵的概念,但从本质上讲,他已经提及缺行真值表,并提出相应的推理规则[4]。限定赋值实质蕴涵包括单赋值实质蕴涵(共四种)、二赋值实质蕴涵(共六种)、三赋值实质蕴涵(共四种)和四赋值实质蕴涵(一种)。其中,单赋值实质蕴涵就是斐洛所举实例所理解的实质蕴涵,这相当于把一个点看作曲线或曲面,或者把函数自变量和因变量的一组确定的值看作函数本身。以此方式理解而得的实质蕴涵导致两个不良后果:一是它无法与许多其它逻辑常项所构成的单赋值真值函项进行有效区分。如在单赋值〈1,1〉的情况下,p→q 与 p∧q、p∨q、p←q及p↔q的真值都为1,这样一来,几个真值形式就无法区别开来;二是以单赋值的实质蕴涵的有效推理规则与充分条件假言推理规则不完全相同。仍以单赋值〈1,1〉情况为例,以p→q为大前提的推理规则有两条,即肯定p可以肯定q和肯定q可以肯定p。但这样一来,推理有效式将得到极大地扩张,然而其存在的合理性却存在疑问。
当然,这两个后果也体现在其它不同赋值数量的实质蕴涵当中。但各种实质蕴涵的类型是否有实际的意义及其深入研究不是本文的目的,在此我们只要证明“→”有不同的意义就足够了。事实上,前件实质蕴涵后件不同种类的存在可以从形式上得到枚举证明。p∨~p→q∨~q和p∧~p→q∧~q是单赋值实质蕴涵;p→p和p→~p是二赋值实质蕴涵;p∧q→p和p→p∨q是三赋值实质蕴涵中充分实质蕴涵;p∧q→~p和p∨q→p是全赋值实质蕴涵。由此我们可以得出这样的结论:当逻辑学用符号“→”做出统一的处理后,不但没有揭示出“如果…那么…”不同用法的共同涵义,反而将其差异和逻辑特性掩盖起来了。正如美国学者科庇所指出的:“→”这个符号“不应被看做表达了‘如果…那么…’或者蕴涵关系的含义,而应看做用‘如果…那么…’这一短语表示的各种不同的蕴涵所共有的局部因素的符号化。”[5]
正是经典实质蕴涵理论把真值与真假等同起来的观点所导致的实质蕴涵的多样性,为我们揭示产生实质蕴涵怪论的根源打开了大门。因为,由此我们可以得出一个重要的结论:在以真值函项理论为基础的有效推理形式中,“→”的每一次出现往往代表不同的实质蕴涵。
我们以文章开头所列出的⑴为例。⑴可以表述为:“如果一个陈述是真的,那么它被任何一个陈述所蕴涵”(如,由于“地球是圆的”是真的,可以推出“现任美国总统是奥巴马蕴涵地球是圆的”)。要说明为什么会出现这样的怪论,我们只需看这一推理的真理形式中“→”两次出现的语义是否相同即可。在⑴的真值表中(如下),我们不难发现:第一,p与q→p的真值组合只有〈1,1〉、〈0,1〉和〈0,0〉三种,但没有〈1,0〉的真值组合,这说明推理的前提p是结论q→p的充分条件;但是,第二,在结论中的q→p,q与 p的真值组合却有〈1,1〉、〈0,1〉、〈0,0〉和〈1,0〉四种,是四赋值实质蕴涵,其中q不是p的充分条件。

p q q→p p→(q→p)1 1 1 1 1 0 1 1 0 1 0 1 0 0 1 1
所以,我们可以得出一个重要的结论:在以真值函项理论为基础的有效推理形式中,“→”的每一次出现往往代表不同的实质蕴涵。一句话,由于把复合命题的真值与复合命题的真假等同起来,导致实质蕴涵理论没有科学地对待真值函项概念而产生多种多样的实质蕴涵,由此使实质蕴涵怪论的产生成为必然。
三、消除实质蕴涵怪论的形式途径
既然我们已经知道实质蕴涵怪论是如何产生的,那么就有可能寻找到某种途径,通过它我们可以有效消除实质蕴涵怪论。当然,这样的途径有语义途径和形式途径之别。语义途径即通过真值方法以判明命题推理形式中“→”在前提中的每一次出现保证为充分实质蕴涵的条件下,其后续的每一次出现是否为充分实质蕴涵,并进而判明命题推理形式是否为实质蕴涵怪论;如果是,则在命题推理系统中取消其定理的地位;如果不是,则保留它,将它视为命题推理系统中的定理。语义途径从实质上讲,是一种对实质蕴涵进行语义限制的方法,以此来消除实质蕴涵怪论。应该说语义途径只是一种理论上的能行途径,但由于可以被称为定理者不计其数,所以不可能通过这种途径完成此项任务。这迫使我们不得不把考察的视野转向形式途径。
科庇提供了由9条推理规则、10条置换规则、(加强)条件证明规则和间接证明规则所构成的命题演算系统。[5]现在我们就以此系统为对象,寻求有效消除实质蕴涵怪论的形式途径。
综观前述推理⑴-⑷,在科庇提供的命题演算系统内如果没有推理规则中的加法规则“p,∴p∨q”(即∨引入规则),⑴-⑷都不能得到有效证明;相反,有了加法规则,它们都可以得到简易而有效的证明。但就是这条规则的地位是十分可疑:它不仅在实际的思维过程中很少得到应用,而且就是借助于它的存在和使用,⑴-⑷才在命题演算中得以产生;更为重要的是,如果我们承认,说推理能够有效进行下去是建立在假定了前提为真的情况下,那么,在假定p的情况之下,所能得出的确切结论是p∨q的真值为真,而不是p∨q的真,这样一来,我们即使能合逻辑地推出~p→q(或~q→p)的真值为真,却无法推出~p→q(或~q→p)的真,否则,就会犯用真值函项的某个真值来取代真值函项真的错误。如果这一结论是真实的,那么如下结论就是正确的:取消加法规则在推理规则中的合法地位就可以消除一切实质蕴涵怪论。另外还有一个强有力的理由来消除加法规则。为了保证推理的有效性,谓词演算系统中的存在例示和全称概括两个规则都对变项是否为自由出现有所限定,而命题演算系统中的加法规则却对变项q的出现没有任何限定,其结果一是结论中出现了在前提中没有出现过、可以作任意解释的同时可能与实际思维过程毫不相关的变项,二就是实质蕴涵怪论的产生。
必须承认,我在这里只是提供了消除实质蕴涵怪论的一种可能途径。这与其说是提供了一种确切的形式方法,倒不如说是提出了一系列有待研究的问题:消除加法规则在科庇命题演算系统内真的能够消除一切命题推理反例和实质蕴涵怪论吗?如果说不能,那么是否存在着其它的途径?如果说能,那么在自然演算SN系统如何消除它们?是否在公理演算系统如弗雷泽系统、丘奇、希尔伯特-阿克曼系统中重新考察其设定公理的合理性(不管怎样,在这些系统中要么以实质蕴涵怪论要么以加法规则为其有效公理)呢?进一步地,当我们实现了这一目标之后,那些为克服实质蕴涵怪论而建立起来的其它系统(如严格蕴涵理论等)是否还有存在的必要呢?在消除了实质蕴涵怪论之后,命题逻辑系统还是完备的吗?这些问题,我并没有找到确切的解决方法和途径,也超出了本文讨论的范围。现在把它们提出来供广大同仁深入探讨。
[1]陈波.逻辑哲学导论[M].北京:中国人民大学出版社,2000:117.
[2]马玉珂.西方逻辑史[M].北京:中国人民大学出版社,1985:258.
[3]斯蒂芬·里德.对逻辑的思考[M].辽宁:辽宁教育出版社,1988:82.
[4]末木刚博.逻辑学——知识的基础[M].北京:中国人民大学出版社,1984:144-145.
[5]I·M·科庇.符号逻辑[M].北京:北京大学出版社,1988:43-81,25.

