求解CVRP 的改进蚁群系统算法

陈 亮，周晶晶

(蚌埠汽车士官学校 运输勤务系，安徽 蚌埠233011)

车辆路由问题(vehicle routing problem，VRP)是分布管理中的核心问题。在CVRP(capacitated VRP)中，一个中心仓库需要给n个客户提供服务。CVRP 的目的是找出一种运货成本最小的路由方式，并且满足:①每个客户只接受1 次服务，而且只有1 辆货车送货给这个客户;②每一辆货车的运货线路都是从货仓出发，并且返回货仓结束;③每一辆货车运货的总质量都不超过自身的质量。由于CVRP 包含了旅行商(traveling saleman problem，TSP)作为其子问题，因此CVRP 是一个NP-难问题。原因是它含有装箱问题，目标是把客户看作物品，把所有的客户“装进”一个供应线路中去。然后，对于每一条供应线路都需要求出访问所有客户的最短访问路线，这又涉及解答TSP。

由于蚁群算法在求解TSP 上取得了一定的成功，许多学者也开始将蚁群算法应用到求解VRP中。Bullnheimer 等［1］提出了一种ASrank-CVRP，这种方法后来又被Reimann 等［2］进行了改进，得到算法ASrank-CVRPsav。这2 种算法均是在ASrank的基础上，使用基于存储启发式方法的启发式信息，并结合最近邻域列表构建路径。国内的研究学者在将蚁群算法用于求解VRP 问题上也作了许多研究，西南交通大学的李军教授和郭耀煌教授对车辆优化调度的基础理论及各类问题进行了系统的研究。刘晓勇等［3］把城市和仓库间的距离矩阵和路径节约矩阵信息融入到初始信息素矩阵中，作为启发式信息引入到蚁群算法中用于求解CVRP。万旭等［4］提出一种基于改进MMAS 的VRP 算法，通过对最大最小信息素策略和信息素更新方式的改进，提高了有时间窗车辆路径质量。张锦等［5］提出一种交叉变异蚁群算法，该算法利用遗传算法对蚁群算法的参数进行优化，然后利用优化后的蚁群算法求解车辆路径问题。总体来说，目前我国对车辆调度问题的理论研究仍相对薄弱，需要进一步研究。

1 改进的蚁群算法

1.1 CVRP 的描述

CVRP 可表描述为完全加权有向图G=(V，A，d)，其中，V= {v0，v1，…，vn}为定点的集合，A={(vi，vj);i≠j}为边的集合。顶点v0为仓库，其他顶点为城市或者客户，非负权重dij与每条边(vi，vj)相关，代表vi和vj间的距离(或者运行时或者运行费用)。对于每一个客户vi，都有一个非负需求qi。CVRP 的目标就是找到一条路由方式使得总运货时间(距离)最小，并且:①每一个客户只接受1次服务，而且只有1 辆货车送货给这个客户;②每一辆货车的运货路线都是从货仓出发，并以返回货仓结束;③每一辆货车运货的总量都不超过自身的载质量。

1.2 路径的构造

蚁群算法求解CVRP，关键在于单个蚂蚁一次迭代如何构建一个可行解，即可行的路径。在一次迭代中，蚂蚁通过一定的规则，选择下一个客户构建路径。同时，蚂蚁在选择下一个客户时，还要考虑蚂蚁的载货量是否满足客户的需要，如果载货量不满足任何一个未访问的客户，就返回货仓再次出发，此时蚂蚁的货物容量重新设置为Q。如此循环，直到所有客户都被访问，就构建了一条可行路径。当所有的蚂蚁均构建路径后，更新信息素完成算法的一次迭代。蚂蚁在选择下一个可访问的客户时，受到2 个要素的影响:一个是当前客户i到选择客户j边上的信息素τij，表示蚂蚁访问完客户i之后立刻访问客户j的期望度，它只与边有关;另一个是启发信息ηij，表示客户i与j间的可见度。在可访问的客户节点集Ω ={vj∈V:vj是可访问的客户}∪{v0}，蚂蚁k按照伪随机比例规则［6］选择城市j作为下一个访问的城市，即

式中:q为均匀分布在区间［0，1］间的一个随机变量，q0(0≤q0≤1);J为根据式(2)概率分布产生的一个随机变量。

式中:α 为决定信息素的相对影响力参数;β 为启发信息素的相对影响力参数;通过调整α、β 来决定残留信息素和启发信息在选择概率的相对作用大小。对于TSP，启发信息被定义为距离的倒数，即ηij=1/dij。

对于CVRP，启发式信息一般是基于存储启发式方法［1-2］，针对CVRP 的存储算法可简单描述为每一对客户(i，j)之间的存储值，即

式中:下标0 为仓库;g和f为参数。

本文采用文献［2］的方法定义启发式信息，即

1.3 信息素的更新

信息素更新有局部更新和全局更新2 种方式。

(1)局部更新。每只蚂蚁从城市i移动到城市j后，就会去掉边(i，j)上一定量的信息素，以增加探索其余路径的可能性。更新规则为

式中:ε(0≤ε≤1)为局部信息素挥发系数;τ0为信息素的初始值。

(2)全局更新。当所有蚂蚁走完全部城市后，仅对最优路径上的信息素进行更新。更新规则为

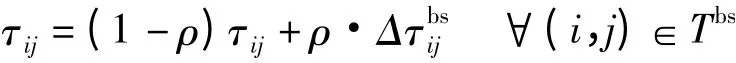
1.4 局部的搜索

在蚂蚁完成路径构造之后，对每条路径的每个子路径采用GIIM 算子［7］优化，以提高解的性能。该算子不仅能防止早熟、跳出局部最优，而且还具有很强的邻域搜索能力［7］。

1.5 基于DT 的候选列表

在求解TSP 中，实验结果表明候选列表可提高ACO 算法所能获取的解的质量，同时也会明显加快求解速度［8］。文献［1—2］采用最近邻域候选列表以提高解的质量;文献［9］研究表明，采用基于DT(delaunay triangulation)策略的候选列表较最近邻域候选列表更优。因此，本文采用基于DT 策略的候选列表。

综合以上要点，得到改进的蚁群算法(IACS-CVRP)流程如下:

读入城市坐标;输出最优路径及长度。

2 实验比较

为了验证改进的蚁群算法(IACS-CVRP)在求解CVRP 问题上的性能，本文采用VRPLIB 的一组基准数据集，数据集分为4 类:A、B、E 和P，每类按规模小、中、大各选择1 组数据。将IACS-CVRP 与ACS-CVRP 及文献［1］ASrank-CVRP 进行比较。本实验全部采用Matlab2010b 编程，运行环境为Window XP sp2、intel Core i3-2100 CPU 3.10GHZ、DDR3 1333MHZ 2GB PC。

2.1 参数设置

ASrank-CVRP 和ACS-CVRP 这2种算法的基本参数设置见文献［1，3］。IACS-CVRP 的参数设置［6］如下:蚂蚁数m为10，迭代次数T为1 000次，α、β、ε 和p分别取1、2、0.1 和0.1，伪随机比例行为选择规则中q0=0.9。

2.2 实验结果

为了更科学、客观地进行比较，实验结果均是算法在相同环境和参数配置条件下运行20 次的平均值(见表1)。Best 为得到的最优解路径长度;Worst 得到的最差路径长度;μ 和σ 分别为运行20次得到解的路径平均长度和标准偏差;T为算法的平均收敛时间。

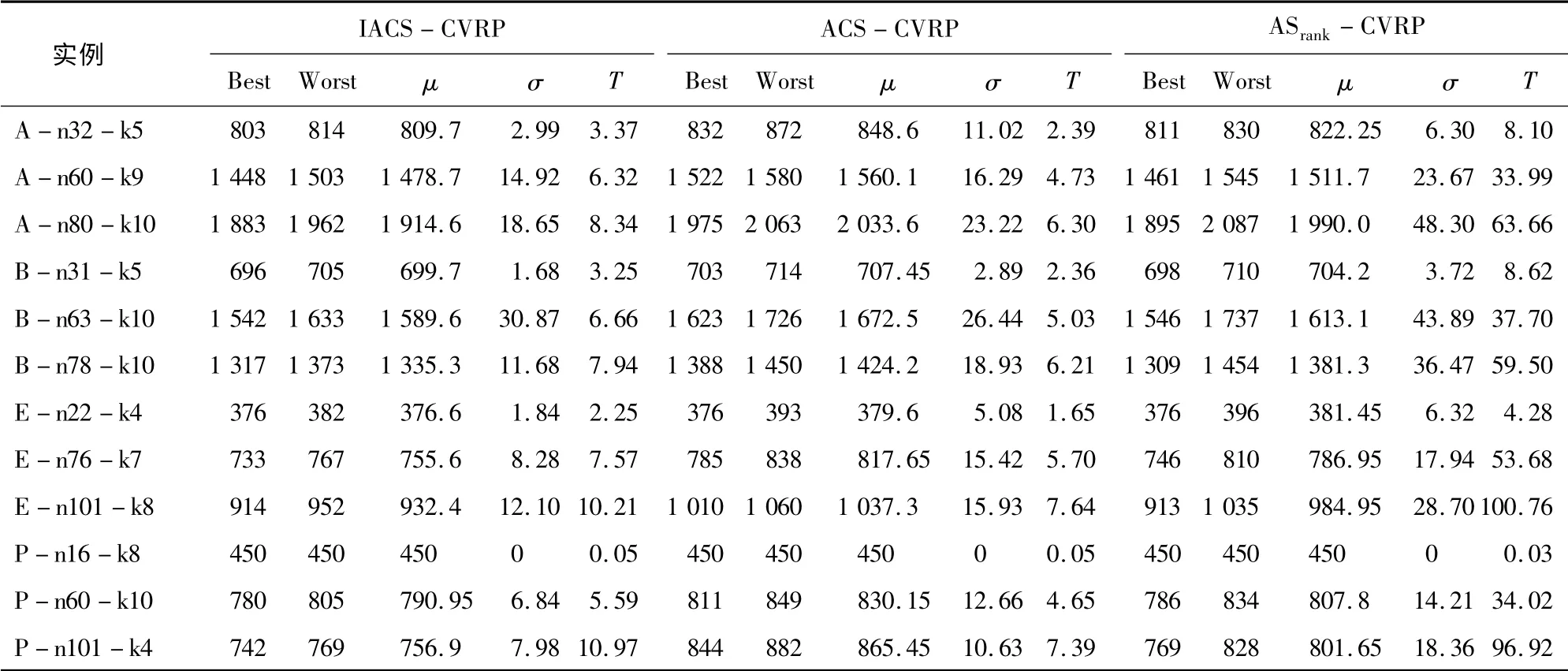
表1 IACS-CVRP 算法与其他算法的总体性能比较

从求得的路径长度(见表1)来看，IACS-CVRP 比另外2 种算法在12 个数据集上获得的最优路径长度、平均路径长度和路径长度标准差都要好，最差路径长度与ASrank-CVRP 相当，并且算法的平均收敛时间较ASrank-CVRP 有很大提高。

3 结 论

本文利用ACS 求解TSP 的优良特性。在ACS的基础上，引入了基于DT 策略的候选列表，提高了构建路径质量;同时在每次迭代中加入了GIIM算子，加强了算法的局部搜索能力。将改进的ACS 算法应用于CVRP，并与2 种蚁群算法在一组数据集上的实验表明，IACS-CVRP 能获得更好质量的解，并且具有较快的收敛速度。

［1］ Bullnheimer B，Hartl R F，Strauss C. An improved ant system algorithm for the Vehicle Routing Problem［J］.Annals of operations Research，1999，89:319-328.

［2］ Reimann M，Stummer M，Doerner K.A saving based Ant System for the vehicle routing problem［C］//Proceedings of the Genetic and Evolutionary Computation Conference(GECCO-2002)，2002:1317-1325.

［3］ 刘晓勇，付辉. 基于启发式蚁群算法的VRP 问题研究［J］.计算机工程与应用，2011，47(32):246-248.

［4］ 万旭，林健良，杨晓伟. 改进的最大-最小蚂蚁算法在有时间窗车辆路径问题中的应用［J］. 计算机集成制造系统，2005，11(4):572-576.

［5］ 张锦，李伟，费腾.交叉变异蚁群算法在VRP 问题中的应用研究［J］. 计算机工程与应用，2009，45(34):201-203.

［6］ Dorigo M，Stutzle T. 蚁群优化［M］. 张军，胡晓敏，罗旭耀，译. 北京:清华大学出版社，2007:75-76.

［7］ 王超学.遗传算法和蚁群算法及其在TSP 问题和配电网重构问题中的应用研究［D］.西安:西安理工大学，2004.

［8］ Gambardella L M，Dorigo M. Solving symmetric and asymmetric TSPs by ant colonies［C］//Proceedings of the1996 IEEE International Conference on Evolutionary Computation(ICEC’96)，1996:622-627.

［9］ 陈亮，李畅. 一种基于知识的快速求解TSP 的蚁群算法［J］. 军事交通学院学报，2013，15(3):78-81.