基于混合模糊神经网络的入侵检测系统

马 乐，赵 锐，阚 媛

(1.军事交通学院 研究生管理大队，天津300161;2.军事交通学院 基础部，天津300161)

随着计算机技术、网络通信以及信息产业的 高速发展，网络入侵攻击的事件频繁发生，计算机网络安全形势日益严峻，迫切需要采取一定的技术手段来保证网络安全。近年来发展起来的一种动态监测、预防或抵御系统入侵行为的安全机制——入侵检测技术是维护网络安全的主要手段之一。它是一种主动防御的安全技术，能够实时地保护内、外网攻击和误操作，使得网络系统受到破坏之前能够及时得到响应和处理。目前，入侵检测技术有许多模型和方法，模糊系统、神经网络等技术的引入使入侵检测的智能型研究成为热点。

模糊神经网络(fuzzy neural network，FNN)融合了神经网络和模糊逻辑特点，从提高神经网络的启发性、透明性和鲁棒性出发，将模糊化概念与模糊推理规则引入神经网络的神经元、连接权和网络学习中。模糊逻辑本身是人工智能领域中的一个重要分支，以模糊逻辑为基础，针对人类思维中模糊性的特点，模仿人的模糊信息识别，解决常规方法难以处理的模糊信息识别问题，成为了人工智能邻域中目标识别的方法之一。神经网络是以人脑神经物理结构为依据，在知识储备和自我学习中发展，从而使人工智能的自组织和并行处理功能得到提高。为了更好地发挥模糊系统和神经网络各自优势、弥补不足，二者结合形成了模糊神经网络。模糊神经网络具备较强的学习和表达能力、自适应性强、能够处理模糊信息等优点，具有广阔的应用前景［1-2］。

1 神经网络与模糊控制相融合的形式

1987 年，美国学者B. Kosko 在他的论文Fuzzy Associative Memories 中第一次对模糊神经网络进行了较为系统的研究，提出了模糊神经网络的概念——具有神经网络与模糊系统的优点，集学习、联想、识别、自适应及模糊信息处理于一体。模糊逻辑与神经网络的融合形式随着研究角度和应用领域的不同而不同，但从系统模型最终实现的功能上看，神经模糊融合的形式归纳起来主要有3种［3］。

(1)神经元模糊模型(如图1 所示)。模型以模糊控制为主体，应用神经元网络实现模糊控制的决策过程，以控制方法为“样本”，对神经网络进行离线训练学习。

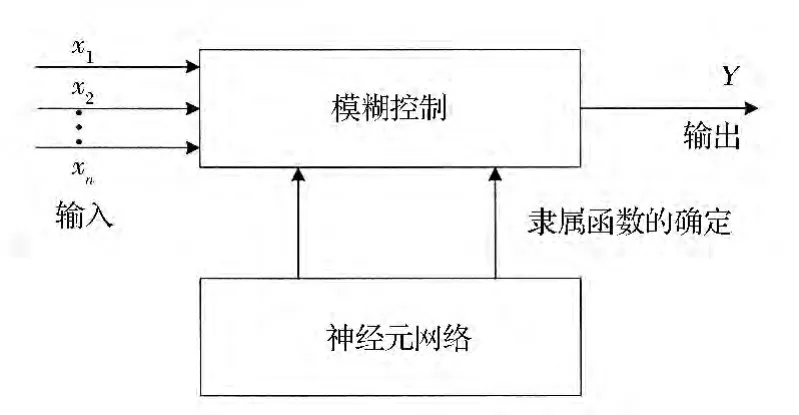
图1 神经元模糊模型

(2)模糊神经模型(如图2 所示)。模型以神经网络为主体，将输入空间分割成若干不同形式的模糊推论组合，对系统先进行模糊逻辑判断，以模糊控制器输出作为神经元网络的输入。

图2 模糊神经模型

(3)神经与模糊混合模型(如图3 所示)。模型中神经网络与模糊系统起着同等重要的作用，它们在系统中各自完成自己的任务，利用各自的长处，相互补充和合作，共同达到统一的目标。神经网络与模糊逻辑系统的组成结构可以根据需求来搭建，一般有并联、串联、串—并联或递阶等结构。

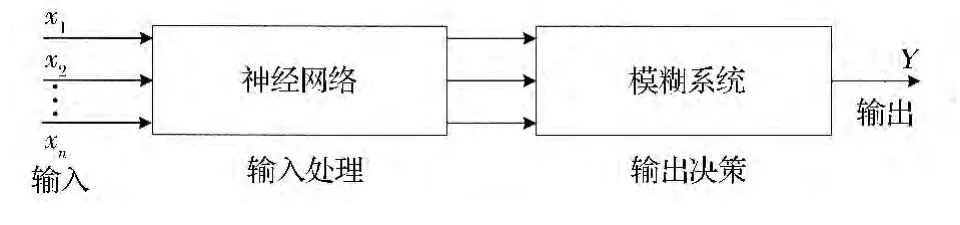
图3 神经与模糊混合模型

该模型结构的神经网络用以完成对输入信号的处理，而模糊逻辑系统用作决策与控制输出。这个系统充分发挥了神经网络的信号处理速度优势和模糊逻辑进行决策和控制中的软推理优势［4］。

2 混合模糊神经网络的网络入侵系统

2.1 入侵检测技术的发展与通用模型

自1980 年入侵检测的概念被提出以来，入侵检测这种主动的网络安全保护技术得到了长足发展。以加州大学戴维斯分校、洛斯阿拉莫斯国家实验室为代表的国内外众多机构开展了入侵检测技术的研究工作，主要集中在基于主机入侵检测系统、基于网络入侵检测系统等方向［5］。自1990年，神经网络、免疫学、遗传算法、信息检索、数据挖掘等技术在入侵检测中的应用而产生的基于智能网络的入侵检测系统，在应对新的网络入侵威胁方面成为一种新趋势。图4 是一个入侵检测系统的通用模型，符合美国国防高级研究计划署提出的通用入侵检测框架CIDF 标准［6］。

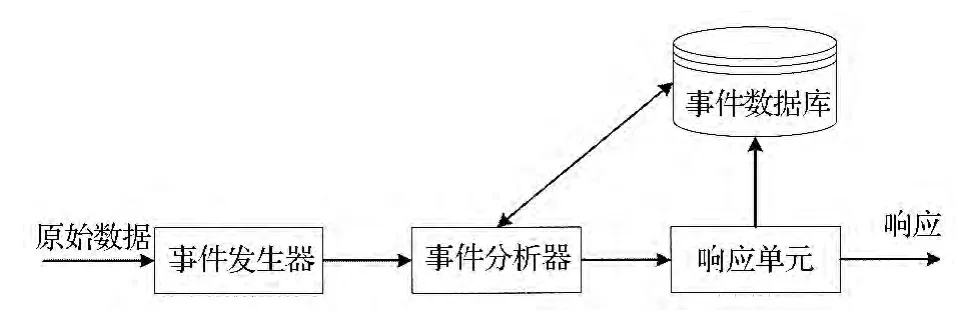
图4 通用入侵检测模型

2.2 混合模糊神经网络入侵检测系统模型

本文选用神经网络与模糊系统混合的结构，来构造入侵检测系统(如图5 所示)。该模型可以分为5 个部分:网络数据获取模块、数据预处理模块、特征提取模块、神经网络模块和模糊控制模块。

图5 混合模糊神经网络入侵检测系统模型

(1)网络数据获取模块。数据获取是进行检测和决策的基础，它的准确性、可靠性和实时性将直接影响到整个系统的性能，模块主要功能是负责网络数据的采集、获取。

(2)数据预处理模块。主要负责对网络原始数据的处理，将网络中的原始数据转化为神经网络可以识别的数据信息，即进行数值化和归一化处理，然后将数据保存为神经网络可识别的标准格式。

(3)特征提取模块。分析数据预处理模块初步处理后的数据，提取神经网络需要的各种输入参数，将提取的符合网络输入要求的特征信息送往神经网络，即去掉冗余属性信息的干扰，将高维的输入特征进行降维。

(4)神经网络模块。整个入侵检测系统的核心，即接收来自特征提取模块处理后的数据，并将其送入已经训练好的神经网络分类器中进行类别检测，输出的检测结果将作为模糊控制系统的输入。

(5)模糊控制系统模块。根据已建立的模糊规则库对输入的分类结果进行决策和判断。根据用户定义的响应形式采取相应的措施或进行相应的报警，包括文字警告、声音警告、电子邮件通知、重新配置路由器或防火墙、关闭连接等［7-8］。

2.3 BP 神经网络模型与改进BP 算法

BP 神经网络是最具有代表性的一种神经网络模型，是当前最流行的神经网络模型之一，得到了广泛的应用。BP 神经网络是一种多层前向型、采用误差反向传播学习算法的神经网络，其结构如图6 所示。它除了输入层和输出层之外，中间还有1 层或多层隐层。在BP 神经网络中同层节点间无任何连接，相邻2 层神经元之间形成全连接。由于同层节点间无任何藕合，因此，每一层的神经元只接受前一层神经元输入，每一层神经元的输出只影响下一层神经元输出。

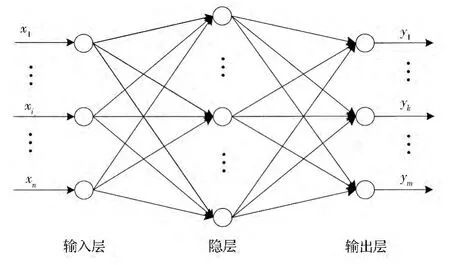
图6 BP 神经网络结构

网络的输入数据X=(x1，x2，…，xn)从输入层依次经过各隐层节点，然后到达输出层节点，从而得到输出数据Y=(y1，y2，…，ym)。可以把BP 神经网络看成是一个从输入到输出高度非线性映射，即f:Rn→Rm，f(X)=Y。

传统BP 算法是采用的最速下降算法(SDBP)，每一次的权值和阈值的修正按式(1)进行，即

式中:x(k)为第k次迭代各层之间的连接权值或阈值向量;为第k次迭代的神经网络输出误差对各个权值或阈值的梯度向量，负号表示梯度的反方向，即梯度的最速下降方向;α 为学习速率，是一个常数。

网络训练开始时，权值初始化为一组随机值，节点输出的期待值是预先规定的，当输入训练数据后，网络的代价函数可以计算出来，通过BP 算法，误差逐层向输入层方向逆向传播，使网络不断自适应地修改网络权值，以减小代价函数值。它采用非线性规划中的最速下降方法，按误差函数的负梯度方向修改权值，通常存在学习效率低、收敛速度慢、易陷入局部最小状态的问题［9］。

为了克服这些不足，在设计神经网络时引入了LM 算法。LM 算法是为了在以近似二阶训练速率进行修正时避免计算Hessian 矩阵而设计的。当误差性能函数具有平方和误差的形式时，Hessian 矩阵可以近似表示为

式中:H为包含网络误差函数对权值和阈值一阶导数的雅克比矩阵;J为对应的横向量。

梯度的计算表达式为

式中e为网络的误差向量。

LM 算法用上述近似Hessian 矩阵按式(4)进行修正

当系数μ 为0 时，即为牛顿法;当系数μ 的值很大时，式(2)变为步长较小的梯度下降法。牛顿法逼近最小误差的速度更快、更精确，因此应尽可能使算法接近于牛顿法，在每一步成功的迭代后(误差性能减小)，使μ 减小;仅在进行尝试性迭代后的误差性能增加的情况下，才能使μ 增加。因此，该算法每一步迭代的误差性能总是递减［10］。

2.4 网络设计

1989 年，Robert H.Nielson 证明了对于在闭区间内的任意一个连续函数都可以用一个3 层(含1个隐层)的BP 神经网络来逼近，因而一个3 层的BP 神经网络可以完成任意的n维到m维的映射，即设计1 个隐层即可。输入层到隐层的传输函数选择双曲正切S 型函数，即

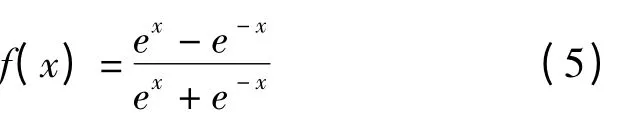
隐层到输出层的传输函数选择对数-S 型函数，即

输入层神经元个数为特征提取后数据的维数，输出层神经元个数为1。

隐层神经元数目的选择是一个十分复杂的问题，需要根据经验和多次实验来确定，不存在一个理想的解析式。参考公式为

式中:m为输神经元数;n为输入单元数;a为［1，10］区间的常数。

3 实验仿真与分析

3.1 实验环境与实验数据

用于实验的计算机配置为Intel Core Duo T6600 @ 2.20 GHz，2 GB 内存，500 G 硬盘。操作系统为Windows 7，仿真实验环境采用Matlab 2010a，实验数据集采用KDD CUP 99。

KDD CUP 99 数据集共包含22 类攻击，分属于4 种入侵类型，即包括拒绝服务攻击(denial of service，DOS)、漏洞探测与扫描攻击(PROBE)、远程非授权访问攻击(remote to local，R2L)和非授权得到超级用户权限攻击(user to root，U2R)。KDD CUP 99 数据集已经完成了数据采集及部分数据预处理、特征提取工作，但在其41 维特征变量中，第2 维协议类型(protocol_type)、第3 维服务类型(service)、第4 维状态标志(flag)均为非数值形式，神经网络无法识别，因此必须进行数值化处理［11］。

数值化编码采取的规则是统计在2、3、4 维中出现的内容，并各自按字母排序，以序号代替原内容。

(1)协议类型。协议类型共有3 种，其编码见表1。

表1 协议类型编码

(2)服务类型。服务类型共70 种，其编码见表2 。

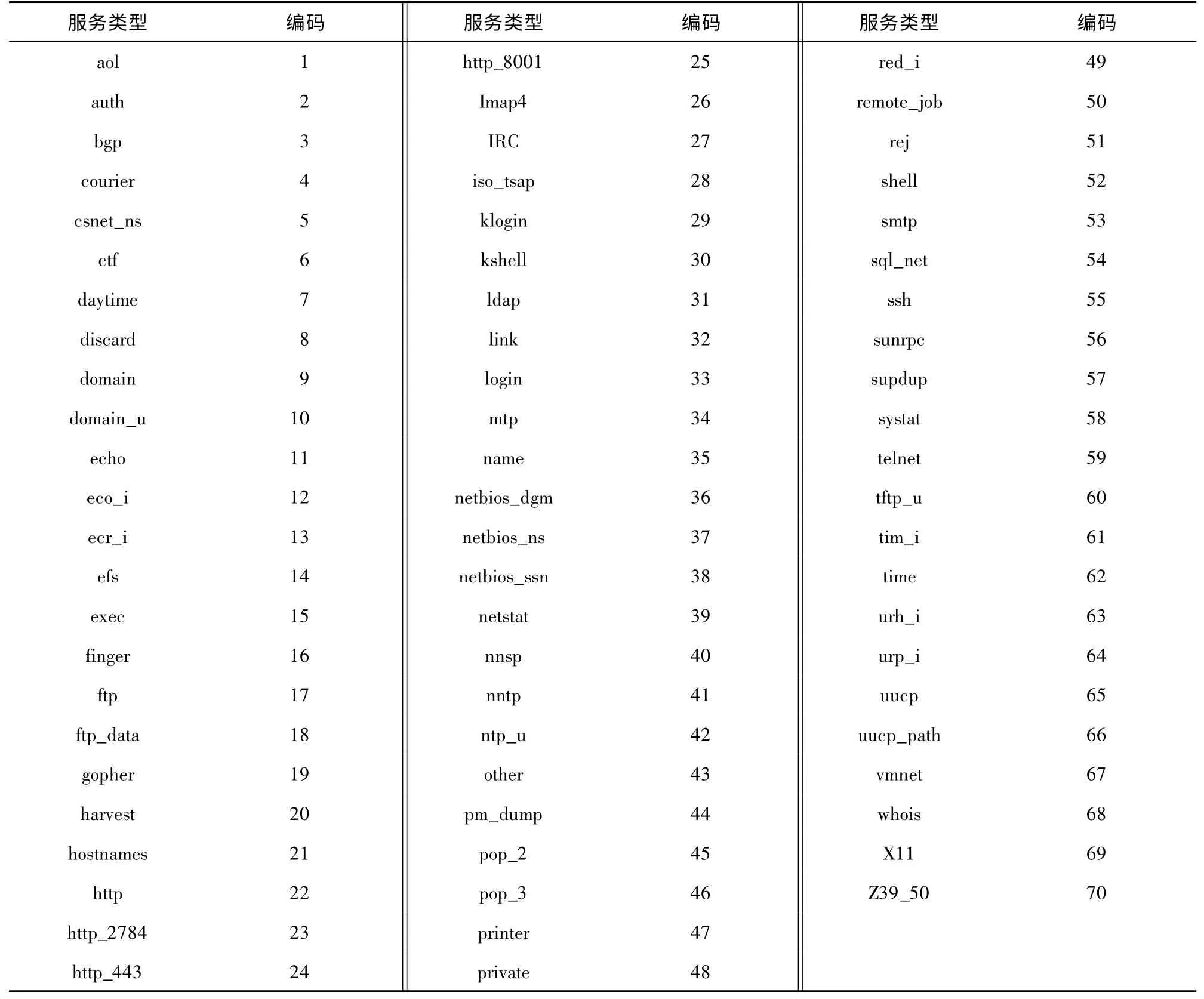
表2 服务类型编码

(3)状态标志。状态标志共有11 种，其编码见表3。

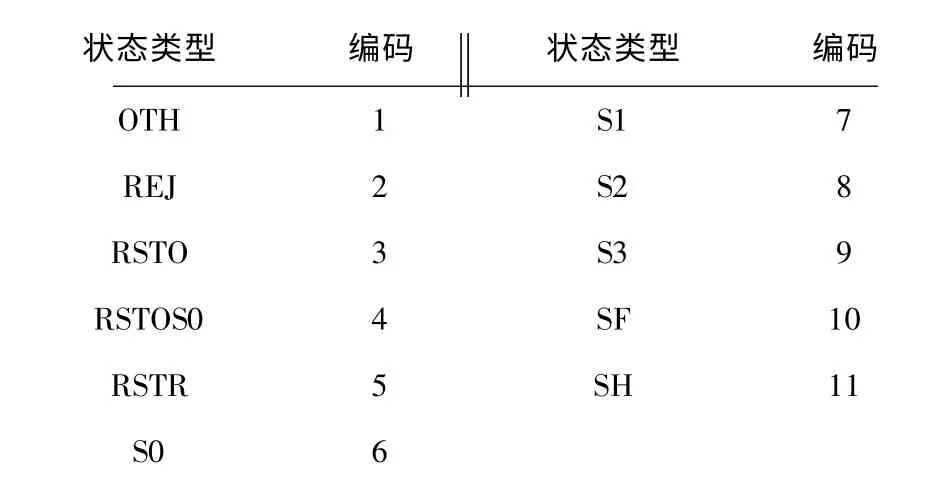
表3 状态类型编码

用SQL server 2008 处理KDD CUP 99 数据集提供的kddcup.data. corrected 文件中的原始数据，删除重复记录，进行数字化编码，构造文本文件，包括训练样本文件Train.txt、训练样本目标输出结果文件Out.txt，以及4 个测试样本文件Test 1. txt、Test 2.txt、Test 3. txt 和Test 4. txt。文件中的攻击(正常)数据均由SQL server 2008 在对应攻击(正常)类型的全部数据中随机选取产生，其中测试样本文件中攻击数据10%，正常数据90%［12］。

3.2 实验结果及分析

误报率和漏报率是检验入侵检测算法的2 个重要指标［13］，分别为

神经网络误差性能目标值为0.01，训练的最大步长为2 000 步，学习率为0.05，最小梯度值为1 ×10-30，网络的训练过程如图6 所示。

神经网络的输出数据位为0 ～1 ，对其进行模糊化处 理，其 中0. 7 ～1 为“yes”，0. 4 ～0. 7 为“maybe”，0 ～0.4 为“no”。再根据先验经验构筑模糊规则库，进行决策与控制输出，实验结果见表4。

图7 LMBP 算法训练的误差性能曲线

表4 实验结果统计

实验表明，改进算法的BP 神经网络较原始BP 算法呈现出了较低的误报率和漏损率，识别效果明显提高，在入侵检测中有着巨大的应用潜力。另外，系统模型中的模糊系统能够在神经网络检测判断的基础上，根据一定的准则构建模糊规则库，为系统的决策实施提供依据。

4 结 语

实验结果表明，LMBP 算法采用在高斯牛顿算法和最速下降算法之间平滑调和的方式，在最初的迭代运算中，函数的斜率比较大，在接近极小值点时，下降速度放慢，使得函数收敛，从而使训练的时间大大的缩短，稳定性得到保证，有效地解决了传统的BP 算法在非线性的迭代计算中不能保证收敛，稳定性差和Hessian 矩阵有可能变成奇异矩阵而无法运算等缺陷。综上所述，基于LMBP 算法的混合模糊神经网络在入侵检测中应用效果良好，精度高，自适应能力更强，学习速度快，能够在很大程度上实现对未知的异常数据包的检测，是一种行之有效的入侵检测方法。通过修改训练样本中的数据进一步发现，检测效率与正常数据的比例有关，即正常数据在训练样本中所占的比重越大，越能区分出攻击数据。

［1］ 曹大元.入侵检测技术［M］.北京:人民邮电出版社，2007.

［2］ 张凯，钱锋，刘漫丹.模糊神经网络技术综述［J］. 信息与控制，2003，32(5):431-435.

［3］ Takagi H.Fusion technology of fuzzy theory and neural networks- survey and future direction［C］//Pro. Int. Conf. on Fuzzy Logic and Neural Networks.1990:13-26.

［4］ 王耀南. 智能信息处理技术［M］. 北京:高等教育出版社，2003:192-196.

［5］ Lough D L. A taxonomy of computer attacks with applications to wireless networks［D］.The Degree of Doctor of Philosophy，Virginia Polytechnic Institute and State University，2001.

［6］ 常佶，陈志坚. 基于CIDF 的网络入侵检测系统设计与实现［J］.内蒙古工业大学学报，2006，25(2):1-2.

［7］ 褚永刚，吕慧勤，杨义先，等. 大规模分布式入侵检测系统的体系结构模型［J］. 计算机应用研究，2004(12):105-106.

［8］ 刘延涛.基于混合神经网络技术的入侵检测模型［D］. 哈尔滨:哈尔滨师范大学，2010.

［9］ 高小伟. BP 神经网络在入侵检测系统中的应用及优化［D］.济南:山东大学，2007.

［10］ 陈海，丁邦旭. 基于神经网络LMBP 算法的入侵检测方法［J］. 计算机应用与软件，2007，24(8):183-188.

［11］ The University of California Irvine KDD Archive［EB/OL］.［2007-06-26］. http://kdd. ics. uci. edu/databases/kddcup99/kddcup99.html.

［12］ 陈晓梅.入侵检测中的数据预处理问题研究［J］. 计算机科学，2006，33(1):81-83.

［13］ Joo D，Hong T，Han I.The neural network models for IDS based on the asymmetric costsof false negative errors and false positive errors［J］.Expert Systems with Applications，2003，25(1):69-75.