基于模糊TOPSIS 方法的军事物流配送中心选址研究

钱 昂，李 欣，石红霞，潘宏达，夏 琰

(1.军事交通学院 研究生管理大队，天津300161;2.军事交通学院 军事物流系，天津300161;3.军事交通学院 综合训练基地，天津300180)

军事物流配送中心是构成军事物流网络的主干实体，在军事物流过程中起到调节流向和流量的作用，它不仅是平战时期物资保障的中心源，也是体现国家军事实力的重要标志;因此，建设强大的军事物流配送中心对满足信息化战争后勤保障需求具有重要意义。军事物流配送中心选址是军事物流配送中心建设的起始步骤，也是其建设的基础，选址的好坏直接影响其保障作用的发挥，对整个军事物流系统有着巨大影响。

军事物流配送中心的选址大多使用定性与定量相结合的综合集成方法，根据不同的目标选择不同的位置。常用的方法有因素评分法、德尔菲法、混合整数规划法、模糊评价法以及计算机辅助决策法。其中模糊TOPSIS 法是有限方案多目标决策的综合评价方法之一，它对原始数据进行同趋势和归一化的处理后，消除了不同指标量纲的影响，并能充分利用原始数据的信息，反映各方案之间的差距，具有真实、直观、可靠、受主观因素影响小的优点。与其他方法相比，具有不受参考序列选择和数据样本多少的影响，应用范围广，信息失真小，灵活简单易行等特点。

1 选址的影响因素分析

(1)军事因素。首先考虑其保障范围，应尽量选择距离所保障部队较近的地区，便于快速及时地提供后勤保障;其次考虑其安全防卫性，应选择较为隐蔽、不易被敌方发现的地区。

(2)经济因素。包括地价因素、离主交通干道距离、周边干线、周边企业状况、所保障的部队分布情况等，尽量减少装卸载次数。

(3)地理因素。地形坡度应在1% ～4% 之间。建设在地形高的地段，容易保持物资干燥，减少物资保管费用;临近河海地区，必须注意当地水位，不得有地下水上溢［1］。应远离闹市或居民区，军事物流配送中心周边不应有产生腐蚀性气体、粉尘和辐射热的工厂，应与易发生火灾的单位保持一定的安全距离，如油库、加油站、化工厂等。

(4)基础设施因素。军事物流配送中心占地规模较大，应充分考虑动力能源供应状况、通信状况、道路设施、废物处理能力等相关基础设施的建设情况［1］。

(5)其他因素。除以上因素外，劳动力条件有时也是军事物流配送中心选址评估的重点之一，有时需要聘请或雇佣地方人员协助完成物资保障任务。

2 选址模型的构建

根据配送中心的实际情况和相关文献的研究成果，本文构建的指标体系分为3 层，如图1 所示。

本文在多人决策的情况下，充分考虑决策者和决策对象的不确定性，将各备选方案的评价指标权重和各指标下的评价值分别用语言变量和梯形模糊数来表示。运用模糊运算法则和模糊排序方法，得到各备选方案的总体评价值，为实际决策提供参考［2］。该方法可以更好地将多个专家的经验知识反映到决策过程中，使决策更加切合实际［3］。

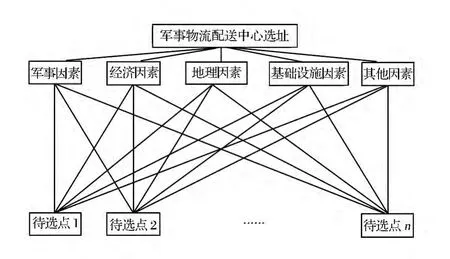
图1 军事物流配送中心选址评价指标体系

在本文提出的配送中心选址评价的模糊层次分析模型中，决策者在给出各指标的权重和评价值意见时，将用到“语言变量”和“梯形模糊数”这2 个基本概念［4］。在评价过程中，专家采用评价值集W={非常低，低，较低，中等，较高，高，非常高}来对指标权重赋值，采用评价值集S= {非常差，差，较差，中等，较好，好，非常好}来评价各指标下关于各备选点的评价值。权重集W和评价值集S的隶属度函数可用适当的梯形模糊数来表示［5］，如图2 和图3 所示。

图2 指标权重对应的语言变量

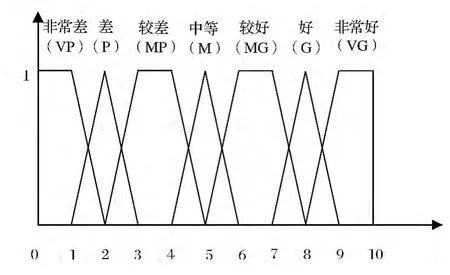
图3 备选点指标权重对应的语言变量

(1)各位专家对指标权重赋值。设评价专家集合为D=(D1，D2，…，Dk)，评价指标集合为C=(C1，C2，…，Cn)。将专家的上述权重语言变量赋值转化为梯形模糊数，即

式中j为指标序号，j=1，2，…，m。集结专家组成员的梯形模糊数赋值，得出群体评价值:

(2)各位专家给出各指标下关于备选点的评价值。将上述针对各备选点的语言变量评价值转化为梯形模糊数，即

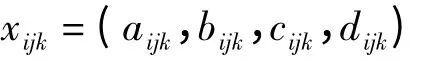
式中i为备选点序号，i=1，2，…，n。集结各位专家的模糊数形式的评价值，可以得出各备选点的专家组群体集结评价值:

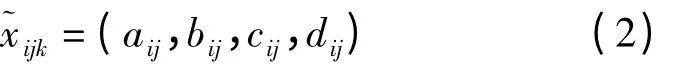
(3)根据上式，可得出指标模糊评价矩阵˜D和指标模糊权重向量˜ω 如下:

(4)对指标模糊评价矩阵进行规范化处理。效益型指标规范化:

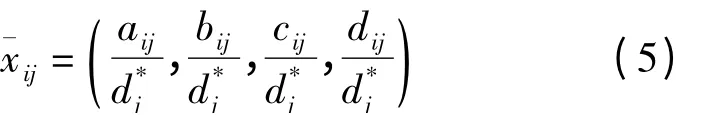
成本型指标规范化:

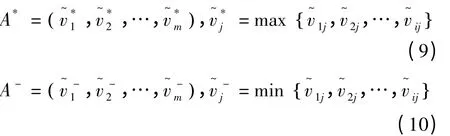
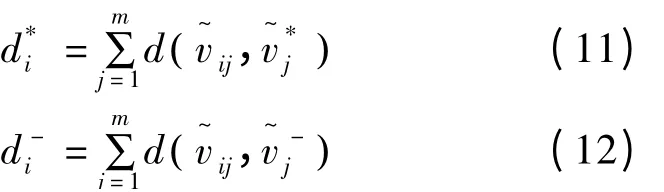
(8)计算贴近度系数，确定备选点如果cci=1，Ai=A*;cci=0，Ai=A-。可见，如果cci越接近1，则Ai越接近理想解A*，cci越接近0，则Ai越接近负理想点［6］。

3 算例分析

假设某部欲建造军事物流配送中心，要在5 个基本符合要求的候选地点中进一步选择各项指标最好的3 个作为军事物流配送中心建设地点，因此需要对这5 个候选地的各项因素进行综合评价。其选址的层析结构模型如图1 所示。

(1)邀请3 位专家(D1，D2，D3)组成委员会对初步筛选得出的5 个候选地(A1，A2，A3，A4，A5)的各项指标进行评价。其评价值见表1。

表1 专家给出的指标权重语言变量评价值

(2)3 位专家组成委员会(D1，D2，D3)给予各指标下(C1，C2，C3，C4，C5)针对各备选点的评价赋值(见表2)。

(3)按照图2 和图3，转化为梯形模糊数，然后根据式(1)、(2)，得出模糊判断矩阵和备选点的模糊权重(见表3)。

表2 专家给出的备选点指标权重语言变量评价值

表3 模糊判断矩阵和备选点权重

(4)按照式(3)—式(6)，将表3 构造加权模 糊矩阵并进行规范化(见表4)。

表4 规范化矩阵

(5)根据上述的加权模糊评价矩阵，可以得出其理想解和负理想解，设正负理想解值分别为(FPIS，A*)和(FNIS，A-)，则

(6)由式(11)、式(12)计算各备选点指标与正负理想点之间的距离，结果见表5 和表6。

(7)根据式(13)计算贴近度系数，确定备选点(见表7)。虑了专家在给出指标权重和备选方案评价值时的不确定性，同时将多名专家意见集成到模糊数中，与传统的AHP 法相比更加直观和易于理解;而且，还可以更好地将多名专家的经验知识反映到决策过程中，使决策更加切合实际，具有较好的应用前景。

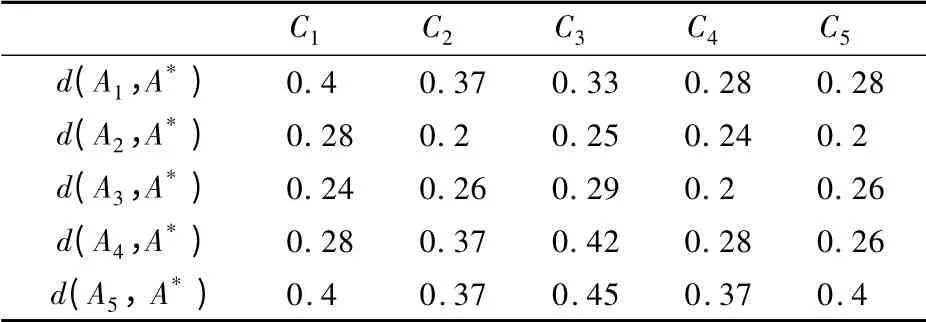
表5 各备选点指标与正理想点之间的距离

表6 各备选点指标与负理想点之间的距离

表7 确定贴近度系数

如果cci=1，Ai=A*;cci=0，Ai=A-。可见，如果cci越接近1，则Ai越接近正理想解A*;cci越接近0，则Ai越接近负理想点。根据表7 中cci的大小进行排序:0.64 ＞0.62 ＞0.51 ＞0.5 ＞0.4，据此确定A2，A3，A4为备选点。

4 结 语

军事物流配送中心选址的影响因素较多，本文充分考虑决策者和决策对象的不确定性，将模糊TOPSIS 方法运用于选址决策中，建立了基于模糊TOPSIS 方法的选址决策模型。由于该方法考

［1］ 王战权，杨东援，汪超.配送中心选址的遗传算法研究［J］.物流技术，2001(3):11-14.

［2］ 龚延成，郭晓汾，蔡团结，等.物流配送点选址模型及其算法研究［J］.中国公路学报，2003，16(2):123-126.

［3］ 张培林，魏巧云. 物流配送中心选址模型及其启发式算法［J］.交通运输工程学报，2003，3(2):65-68.

［4］ 孙亮，汪晓霞，郑吉春. 物流中心选址评价指标体系设计［J］.物流技术，2006(10):26-28.

［5］ 夏玉森，周海云.模糊综合评判在军事物流中心选址中的应用［J］.包装工程，2006，27(1):142-143.

［6］ 关志民，周宏波，马钦海. 基于模糊多指标评价方法的配送中心选址优化决策［J］. 东北大学学报:自然科学版，2005，26(8):801-804.