基于云模型-AHP 的运输勤务训练场保障效能评估

朱 亮，张武军，田 海

(1.蚌埠汽车士官学校 训练部，安徽 蚌埠233011;2.蚌埠汽车士官学校运输勤务系，安徽 蚌埠233011)

训练一直是部队的热点问题，尤其是习主席 提出“能打仗、打胜仗”的强军目标后，部队训练逐步向实战化聚焦，部队运输勤务训练问题亦是如此。针对部队运输勤务训练场普遍存在场地设施不足、训练器材缺少、训练内容陈旧等问题，总部加大投入，制定并落实“十二五”期间部队运输勤务训练场建设规划，进一步加强部队运输勤务训练基地化、现代化的目标，不断提高部队军交运输专业训练的质量和效益，各部队都加强了汽车运输勤务训练场的建设［1］。在建设投入使用后，对各个训练场的总体评价以及各个训练场之间的评比就变成总部迫切需要解决的问题。传统意义上的评价，一般采用总部选派专家，专家依照一定的标准进行现地评价，总体上是一种人为的、主观上的一种评价方式，受人为影响因素较大，科学性明显不高。

运输勤务训练场涉及场地、车辆、保障设施等众多要素，难以建立一套纯定量的方式来进行评估。效能评估是对某种事物或系统执行某一项任务结果或者进程的质量好坏、作用大小、自身状态等效率指标的量化计算或结论性评价，广泛用于军事、科研、制造行业，也可用于评估某种计划、工程。因此，笔者设想用效能评估对运输勤务训练场进行评价，提出运输勤务训练场保障效能评估，从运输勤务训练场保障功能、过程、效果等方面进行评价。本文从运输勤务训练场保障效能入手，提出基于云模型-AHP 的运输勤务训练场保障效能评估，给出详细算法，最后进行实例分析。验证结果表明，基于云模型-AHP 进行运输勤务训练场保障效能评估可行、有效。

1 运输勤务训练场保障效能评估

1.1 基本概念

运输勤务训练场，是为了满足部队运输勤务训练而设置的场地，一般包括铁路输送训练场地、水路输送训练场地、配置展开训练场地、障碍路段训练场地等等。运输勤务训练场保障能力是指其保障部队训练数量、质量等相关方面的能力，如运输勤务训练场一定时间内能保障多少部队同时训练、能保障部队训练多少课目等方面的能力。对运输勤务训练场保障效能进行评估，就是运输勤务训练场保障效能评估。

1.2 评估方法分析

运输勤务训练场保障效能评估涉及的要素比较多，很难准确地对其进行有效的评估，需要一种评估方法，能够充分考虑到评估过程中出现的模型，同时又能够有效而简便地实现定性与定量相互转换。层次分析法(AHP)是20 世纪中期提出的多准则决策方法。它把一个复杂的问题表示为一个有序的递阶层次结构，通过构造两两比较矩阵计算各子指标层的相对权重，从而得出系统的效能值。该方法将定性和定量分析相结合，是分析、评估多目标、多准则的复杂系统的有力工具，具有思路清晰、方法简便、适用面广、系统性强等优点，但其属于主观评估法，由专家打分的方式获得判断矩阵，所以评估结果有较强的主观性［2］。模糊综合评判法是在模糊集理论的基础上，应用模糊关系合成原理，对被评判对象隶属等级状况进行综合评判的一种方法［3］。其优点是可以较好地解决包含难以精确定量表达的评价因素的评估问题，其缺点是不能给出具有明确物理意义的定量评估结果，并且隶属函数的建立在很大程度上依靠经验，需要在实践中反复修正，才能得出适合具体问题的隶属函数。Lanchester 方程法就是基于兰切斯特战斗理论的一种效能评估方法。它在一些简化的假设前提下，建立了一系列描述交战过程中双方兵力变化数量关系的微分方程组，通过战斗效能比和交换比等指标的计算得出效能评估结果［4］。随着信息技术的发展，李德毅院士提出一种定性定量互换模型——云模型，它作为不确定性人工智能的重要理论和工具，把空间实体的模糊性和随机性集成到一起，在一定程度上克服了以上方法的局限性，能较好地处理定性定量信息的互相转换，尽最大程度地减少人工干预，为定性定量相结合的信息处理提供有力工具，可以有效地实现系统效能评估［5］。综合以上评估方法，本文提出用层次分析法建立评估指标和权重，用云模型来进行运输勤务训练场保障效能评估。

1.3 评估指标体系及权重

指标体系采用层次分析法。首先分析军车交通安全风险构成要素，建立树状的关系结构，运用目标层次分类展开法，将目标按逻辑分类向下展开为若干目标，再把各目标分别向下展开成分目标和准则，以此类推，直到可以定量或可进行定性分析为止，从而建立一套初步的指标结构体系。然后利用德尔菲法对初步的指标体系进行完善与确定。德尔菲法的基本步骤为:一是选择咨询专家组，不少于10 人;二是设计调查表，进行专家组问卷调查;三是回收调查表并进行统计处理，以此统计结果为依据，制作第二轮调查表，这样循环往复直至调查数据趋于一致;四是统计数据，整理最终的调查报告，得出最终的评价指标体系。

在建立层次结构体系后，由于各层次元素的权重界定比较困难，所以在上层的评定标准下，对本层次元素互相的重要性进行两两比较，取1→9值对各自的重要性进行赋值，进行量化从而可以构造各层次的指标判断矩阵A=［aij］:

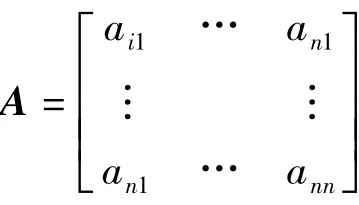
式中n为对进行判断的相邻下一层的指标因素数。

(1)判断矩阵A的最大特征向量:

最大特征值对应的最大特征向量为

(2)计算A的最大特征值:

(3)一致性检验。进行一致性检验后得到各指标的相对权重。

依照上述方法，建立部队运输勤务训练保障效能指标体系及权重表(见表1)。

2 建立基于云模型-AHP 的评估数学模型

2.1 云及隶属云的基本理论

云是用自然语言值表示的某个定性概念与定量表示之间的不确定性转换模型，具有直观性和普遍性。它主要反映概念上的不确定性，即模糊性(边界上的亦此亦彼性)和随机性(发生的概率)［6］。云的数字特征用3 个参数来描述，即期望值Ex、熵En和超熵He，3 个数字特征整体表征一个概念，记CG(Ex，En，He)。其中期望值Ex为概念上的原型值(中心值、标准值)，最能代表这个定性概念的数值;熵En为概念不确定程度的度量，熵越大，概念相对越模糊;超熵He为熵的不确定程度的度量，即熵的熵，反映了云的离散程度。当所研究的问题是纯随机问题时，Em→∞n，为纯模糊问题时，En=0。

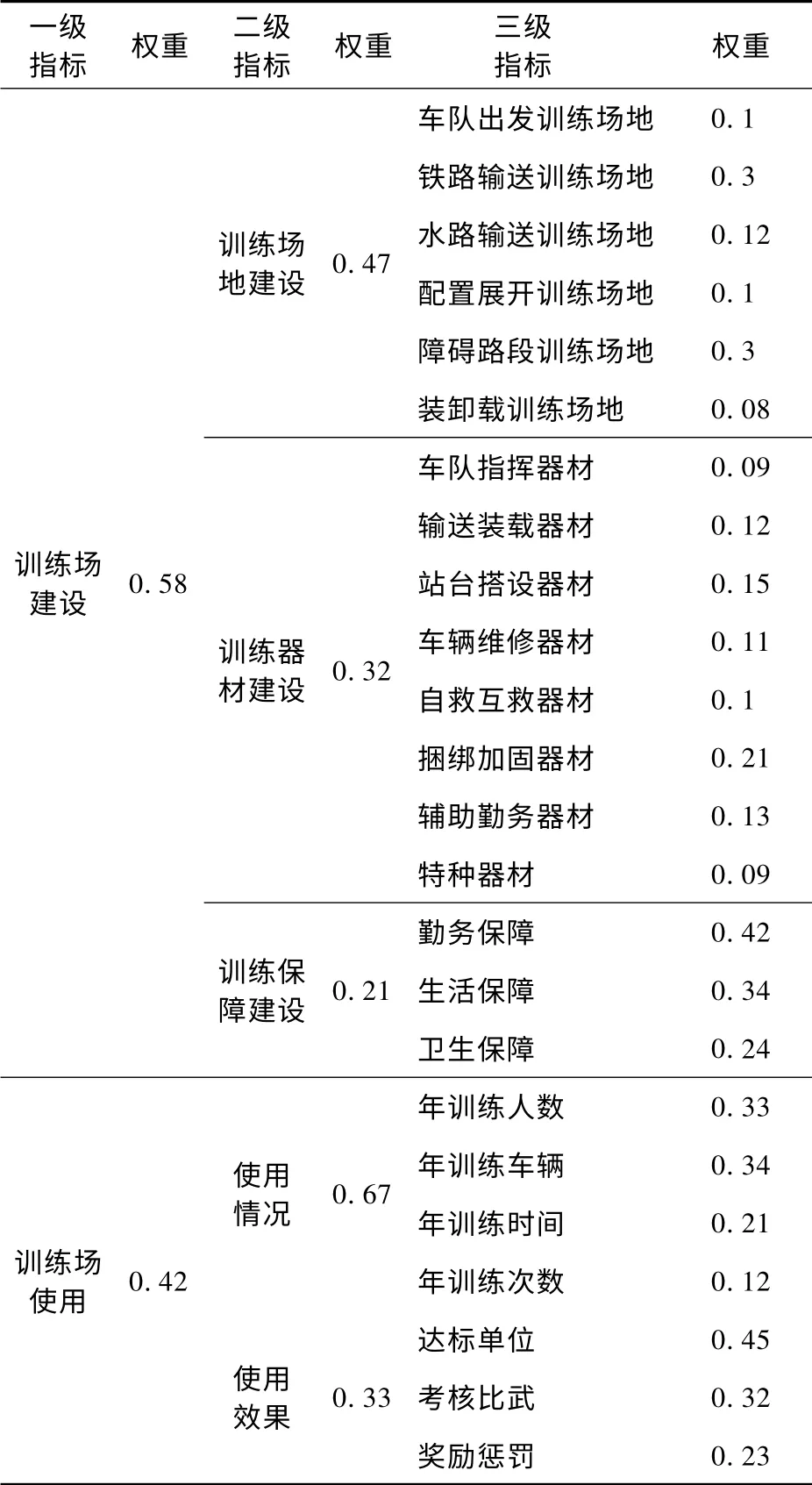
表1 部队运输勤务训练场保障效能指标体系及权重

2.2 云重心评估法

云重心可以表示为T=a×b。a表示云重心的位置，b表示云重心的高度。期望值反映了相应的模糊概念的信息中心值，即云重心的位置。当期望值发生变化时，它所代表的信息中心值发生变化，云中心的位置也相应改变。在一般情况下，云重心的高度通常取常值(0.371)，期望值相同的云可以通过比较云重心高度的不同来区别它们的重要性，即云重心高度反映了云的重要性。

其具体评估步骤如下:

(1)各指标的云模型表示。在给出的指标体系中，提取n组样本组成决策矩阵，其云模型为式中En=［max(Ex1+Ex2+… +Exn)-min(Ex1+

同时，每个语言值的指标都可以用云模型表示，那么n个语言值的表示方法为

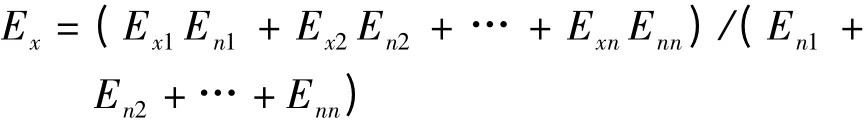
式中En=En1+En2+… +Enn。当指标为精确数值型时，“Ex1-Exn”为各指标量的值;当指标为语言值时，“Ex1-Exn”为指标云模型的期望，即指标云模型的熵。

(2)系统状态的表示。n个性能指标可用n个云模型来刻画，n个指标所反映的系统状态可用n维综合云表示。对于n维综合云的重心T用一个n维向量表示，即

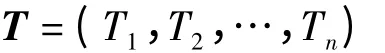
式中Ti=ai×bi，i=1，2，…，n。当系统发生变化时，其重心变化为T'=(T'1，T'2，…，T'n)。

(3)确定各指标体系的权重wi。

(4)加权偏离度的计算。理想状态下，n维综合云重心的位置向量，高度为b=(bi)1×n，其中bi=wi×0.371。云重心的向量T0=a×bT=(T0i)1×n。同理可得，一定状态下系统n维综合云重心的向量T=(Ti)i×n，进行归一化，可得

经过归一化，表征系统状态的综合云重心向量均为有大小、有方向，无量纲的值，把各指标归一化之后的向量值乘以其权重值，再相加，取平均值后得到加权偏离值θ(0≤|θ|≤1)的值为

(5)评估模型语集的确定。评语集V= (极差，非常差，很差，差，较差，一般，较好，好，很好，非常好，极好)构成一个定性评测的云发生器。

3 实例分析

以某部队运输勤务训练场为实例，以其训练场地建设为研究对象，运用云模型对其进行效能评估，其余的效能评估类似。训练场地建设指标有车队出发训练场地、铁路输送训练场地、水路输送训练场地、配置展开训练场地、障碍路段训练场地和装卸载训练场地，以4 名专家进行定性检查的结果情况进行评估分析，结果见表2。

表2 指标状态

利用云模型把语言值用相应的3 个特征值(Ex，En，He)来表征，即用一个云对象来表示，并由此组成决策矩阵:

由B求得各个指标云模型的Ex，En(见表3)。

6 个指标的权重值wj=(0.1，0.3，0.12，0.1，0.3，0.08)，则该六维加权综合云重心向量T=(0.047 5，0.202 5，0.045，0.055，0.195，0.032)，理想状态下加权综合云重心向量T0=(0.1，0.3，0.12，0.1，0.3，0.08)，归 一 化 后 得 到TG=(0.525，0.325，0.625，0.45，0.35，0.6)，加权离散度θ=0.423，距离理想状态下的加权偏离度为0.423，即最终评价结果为0.577，对应评价结果介于“一般”与“很好”中间，倾向于“很好”。同理，可以依此方法对所建立的评估体系的其他指标进行评估，给出最终评价结果。

表3 各指标云模型的期望值和熵

4 结 语

对运输勤务训练场保障效能评估是一个复杂的过程，既有主观上的评价，又需要有可行的评估模型和方法。本文提出的基于云模型-AHP 的运输勤务训练场保障效能评估方法，较好地解决了评估的模糊性和随机性，很好地结合了定性的评估结果和定量的评估模型和方法，去除了系统的不确定性，为下一步总部开展运输勤务训练场建设考核，改进部队运输勤务训练场保障效能评估有一定的参考价值。

［1］ 周和平，单忠年.浅谈运输勤务训练场建设现状与对策［J］.国防交通，2012(4):53-54.

［2］ 段维清.基于层次分析法的微格教学评价模型的构建［J］.太原师范学院学报:自然科学版，2012，26(3):34-36.

［3］ 李伯虎，柴旭东，李潭.复杂系统高效能仿真技术研究［J］.中国电子科学研究院学报，2012，7(3):55-58.

［4］ 陈向勇，井元伟，李春吉. 基于Lanchester 方程的作战混合动态系统最优变招控制［J］. 控制理论与应用，2012，29(6):28-31.

［5］ 张磊，李晓霞，艾伶俐，等.基于模糊综合评判法的营运车辆使用可靠性评价［J］. 山东交通学院学报，2012，20(3):22-25.

［6］ 李存斌，周小萌，杜哲. 基于云模型的风险智能预测方法［J］.科技与管理，2012(6):46-49.