多功能工程车最佳动力性换挡规律

蒋美华，刘咏标，陈 欣，苏俊刚

(1.军事交通学院 国家应急交通运输装备工程技术研究中心，天津300161;2.军事交通学院 研究生管理大队，天津300161;3.军事交通学院 军用车辆系，天津300161;4 蚌埠汽车士官学校 学员旅，安徽 蚌埠233000)

换挡规律是指2 个挡位之间自动换挡时刻随控制参数变化的规律，最佳换挡规律是指以获得较好的动力性为目的的换挡规律［1］。工程车辆换挡通常模仿汽车换挡规律而采用二参数或者三参数自动换挡技术，然而这些都是以发动机和车辆稳态为前提，即都是静态的换挡规律。多功能工程车在实际运作时处于非稳定状态，并且要兼顾高速行驶与低速作业2 种工况。鉴于此，本文提出了行驶工况三参数(车速、加速度和油门开度)和作业工况四参数(牵引力、油门开度、车速和工作装置液压系统压力)相结合的动态换挡策略，并利用Matlab 对最佳换挡点参数进行运算求解。

1 行驶工况三参数最佳动力性换挡规律

反映发动机和车辆工作状况的基本参数是车速和油门开度，一般自动换挡都以它们作为确定挡位的基本参数。若仅采用车速或油门开度中的一个参数作为换挡参数，即所谓的单参数换挡是不合理和不全面的。若采用油门开度作为控制参数，大油门升高挡，小油门回低挡，则无法在低挡发挥大牵引力;若采用车速作为控制参数，油门开度变化不能影响换挡点变化，则势必造成动力性和经济性难以兼顾的后果。试验表明，静态与动态换挡点速度的最大误差可达13%以上［2］，油门开度越大，加速度越大，则误差越大。因此，行驶工况下的换挡规律应采用能够反映真实动态过程的3 个参数——车速v、加速度a和油门开度α 作为控制参数，才能使车辆真正发挥出其最佳性能。

同一油门开度下相邻2 个挡位的加速度曲线交点为换挡点，即

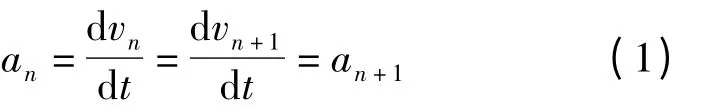
式中an、an+1分别为同一油门开度下第n挡、第n+1 挡的加速度。

将不同油门开度下相邻2 个挡位的加速度交点连成曲线，即为最佳动力性换挡特性，将其转换到油门开度与速度关系图上就是最佳动力性的换挡规律。严格来说，反映加速度对换挡规律的影响，应以加速度、速度和油门开度确定的空间坐标来表达。式(2)给出了任意挡位的加速度表达式:

式中:Ftn为变速器第n挡驱动力;Ff为滚动阻力;Fwn为变速器第n挡时车辆的空气阻力;m为汽车质量;δn为第n挡考虑了发动机非稳定特性以及旋转惯量影响的回转质量换算系数，且

式中:Iw为车轮的转动惯量;If为飞轮的转动惯量;r为车轮滚动半径;ηT为传动效率;ign为变速器n档传动比;i0为主减速比;λ 为发动机非稳定状态下转矩的下降系数。

根据同一油门开度下相邻2 个挡位的加速度相等得到

式中Fn、Fn+1分别为同一油门开度下第n挡、第n+1 挡的行驶阻力。

发动机转矩与转速的关系Te+f(ne)可拟合为二次曲线，即

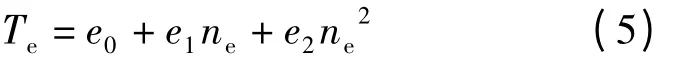
式中e0、e1、e2为转矩回归系数。则变速器第n挡驱动力为

行驶阻力为

车辆的行驶阻力可以用车速的二次函数表示，即

式中:h0=Gf，G为作用于汽车上的重力，f为滚动阻力系数;h1=CdA/21.15，Cd为空气阻力系数，A为迎风面积。

将式(6)和式(8)代入式(4)化简得

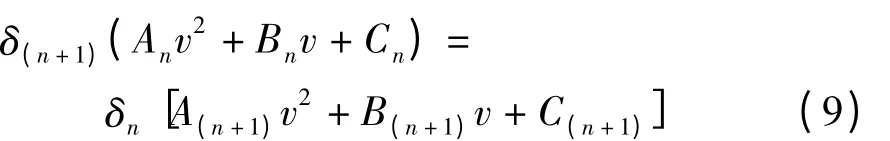
即

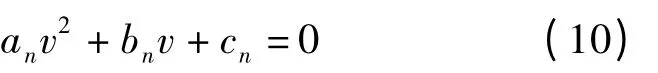
则相邻2 个挡位的最佳动力性换挡点速度为

2 作业工况四参数最佳动力性换挡规律

作业工况下多功能工程车的动力性主要取决于牵引力特性，因此，研究其换挡规律时应采用牵引力、油门开度和车速作为控制参数［3］。此外，由于与行驶工况相比，作业工况还加入了工作装置的运行，工作装置中液压系统的油压也是影响换挡规律的一个重要参数。故对于多功能工程车，在研究其作业工况下的换挡规律时，应选择牵引力、油门开度、车速和工作装置液压系统压力4 个参数作为控制参数。

在已知油门开度的情况下，换挡点的车速计算需要考虑工作装置所消耗的转矩［4］，也就是发动机输出转矩需扣除工作油泵消耗的转矩后与液力变矩器进行匹配，故发动机输出到液力变矩器的转矩为

式中:Tp为扣除工作油泵消耗后发动机的输出转矩;Te为发动机转矩;Mg为工作油泵消耗转矩，且

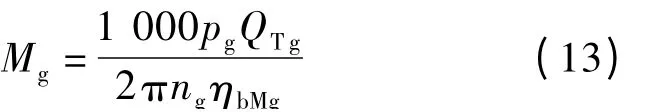
式中:pg为工作油泵的输出压力;QTg为工作油泵的流量;ng为工作油泵的转速;ηbMg为工作油泵的机械效率。

通过发动机与液力变矩器的匹配，得到液力变矩器涡轮轴的输出转矩Tt，通过拟合可得

式中nt为涡轮轴转速。

多功能工程车在低速作业工况下对牵引力的要求较高，按照最佳动力性换挡的原则，取相邻2个挡位牵引力曲线的交点为换挡点［5-6］，即

将式(14)代入式(6)，根据式(15)整理简化可得

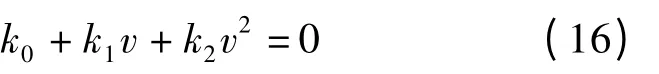
则相邻2 个挡位的最佳动力性换挡点速度为

3 实例分析

3.1 2 个工况下的输出特性

以某多功能工程车为例，其基本参数见表1。

表1 某多功能工程车基本参数

选择油门开度为100%工况点，在作业工况下考虑工作装置液压系统额定压力，即工作装置全负荷运转。行驶工况和作业工况发动机与液力变矩器共同工作输出特性分别见表2 和表3。

表2 行驶工况发动机与液力变矩器共同工作输出特性

表3 作业工况发动机与液力变矩器共同工作输出特性

利用Matlab 对数据进行多项式计算，得行驶工况下发动机与液力变矩器全功率匹配后，涡轮轴输出转矩特性为

作业工况下发动机与液力变矩器部分功率匹配后，涡轮轴输出转矩特性为

3.2 行驶工况最佳换挡点车速

行驶工况下换挡点计算选取全油门工况时最佳动力性升挡点。由式(18)已知的涡轮轴输出转矩特性，结合式(4)通过Matlab 编程得到该工况下的加速度—速度曲线(如图1 所示)。根据换挡点加速度相等的原则，由已知参数联立式(6)得到最佳换挡点车速及其对应参数(见表4)。

图1 行驶工况加速度曲线

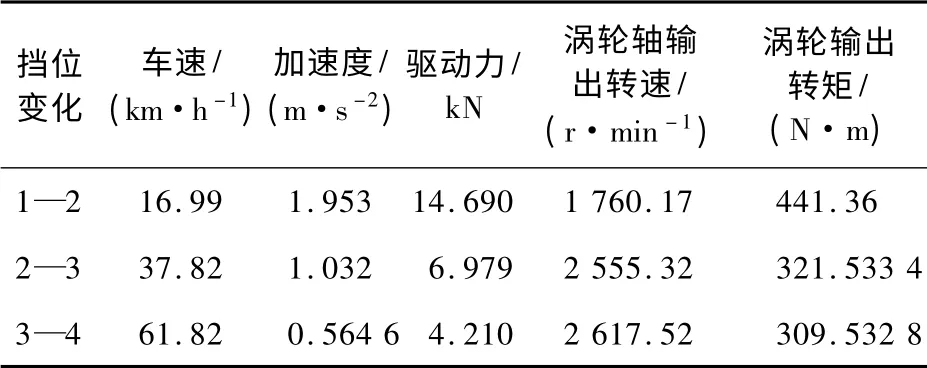
表4 行驶工况最佳换挡点参数

3.3 作业工况最佳换挡点车速

计算选择作业工况工作装置液压系统额定压力下发动机油门全开的升挡点。如前所述，发动机转矩扣除工作装置消耗转矩后与变矩器部分功率匹配，由式(19)中已拟合的涡轮轴输出转矩特性，结合式(15)通过Matlab 编程绘出各挡牵引力特性曲线(如图2 所示)。根据相邻2 个挡位换挡点牵引力相等的最佳换挡原则，结合计算公式得到该工况下最佳换挡点车速及其对应参数(见表5)。

4 结 语

本文通过分析影响多功能工程车在行驶与作业2 种工况下的最佳动力性换挡规律的主要参数，研究确定了多功能工程车最佳动力性换挡规律的方法。并根据确定的多功能工程车最佳换挡规律的方法，建立了多功能工程车在不同工况下的最佳动力性换挡规律数学模型。

图2 作业工况牵引力曲线

表5 作业工况最佳换挡点参数

通过实例分析，利用Matlab 仿真得出不同工况下影响换挡规律的特性曲线，求取了在发动机全油门开度下换挡点车速及其对应参数。可见，采用行驶工况三参数和作业工况四参数相结合的动态换挡策略，可更加准确地求出最佳换挡点。

［1］ 张勇，刘杰，宋健，等.汽车不同质量参数的最佳动力性换挡规律［J］.同济大学学报，2005(9):70-73.

［2］ 葛安林，车辆自动变速理论与设计［M］. 北京:机械工业出版社，1991.

［3］ 崔功杰，赵丁选.动态四参数工程车辆的自动换挡规律［J］.西安交通大学学报，2008(9):1099-1102.

［4］ WEILHG，PROBST G，GRAF F. Fuzzy expert system for automatic transmission control application［C］//The 1st IEEE Conf Fuzzy Systems，San Diego，CA，USA，1992:716-721.

［5］ 张勇，刘杰，卢新田，等.工程车辆自适应模糊换挡决策方法［J］.同济大学学报，2005(1):104-108.

［6］ 张国胜，方宗德，牛秦玉. 最佳动力性换挡规律的制定与仿真研究［J］.机械科学与技术，2005(7):768-770.

［7］ 将美华，邵宏，张磊，等. 高速工程车匹配性能分析研究［J］.机械工程，2008(5):39-42.