基于证据推理的设计方案多属性决策新方法
卢章平,李小蕾,袁 浩,刘 明
(江苏大学机械工程学院,江苏镇江212013)
概念设计方案评价是一个典型的不确定多属性决策问题,是近年来决策研究中的一个重要内容,具有广泛的应用背景.处理多属性决策问题的方法有很多种,也各自存在一些不足,例如,层次分析法是在评价决策中应用较多的一种方法[1-3],通过两两比较进行评价决策,缺点在于对不确定信息缺乏充分考虑,且两两比较矩阵难以保证一致性;模糊评价法主要有模糊综合评价法和改进的模糊综合评价法、模糊优序法等[4-6],利用隶属度及模糊推理等方法对概念方案进行排序,不足在于确定隶属度较困难易造成评价误差;TOPSIS方法[7]和多属性效用理论[8]往往只考虑定量指标忽略定性指标,而现实中的多属性决策问题,尤其是概念设计方案评价问题常包含定性属性;证据推理法也称为Dempster-Shafer证据理论,是由 Dempster首先提出、后由 Shafer进一步发展的一种不精确推理理论,由于它能够处理不确定和不完全信息,所以在概念设计方案评价中有着广泛的应用[9-13],但证据推理在概念设计方案决策应用过程中存在一些缺陷.首先,证据推理算法要求目标属性的权系数是确定且完全的,在已有的证据推理方法中,权重大多采用主观赋权法,由于决策者对问题认识或自身知识的局限性,给出的权重太主观且无实际意义,有些文献也提出构建客观权重,如文献[10-11]引入信息熵的概念,利用熵权求得各属性的客观权重,但决策结果显示方案排序不完全一致,仅依据评价系统中数据确定权值绝对客观,有可能产生与实际相悖的权值;其次,证据推理算法要求基本属性与广义属性应具有相同的评价集,这在实际决策中较难做到,特别是对定性的基本属性.
为了克服这些问题,文中以证据推理决策这一最具代表性的决策方法为基础,引入反偏好函数的概念,利用主客观因素相结合的反偏好函数法确定目标属性的权重,以便决策者做出更合理的决策;通过建立不同反偏好阶段的区间边界值,确定统一的模糊评价集,以解决传统证据推理评价中定性定量指标分别构建评价集及评价集的统一处理等一系列复杂的问题.
1 基于证据推理算法的多属性决策
应用证据推理进行方案评价决策时把各个基本属性ei看成相应的证据,将评价等级H={Hn|n=1,2,…,N}看成辨识框架,方案的评价决策问题可以用不同证据E={ei|i=1,2,…,L}下各方案A={al|l=1,2,…,M}相应的期望程度及依据ER算法构造的基本概率分配函数mn,i(al)表示[12]为
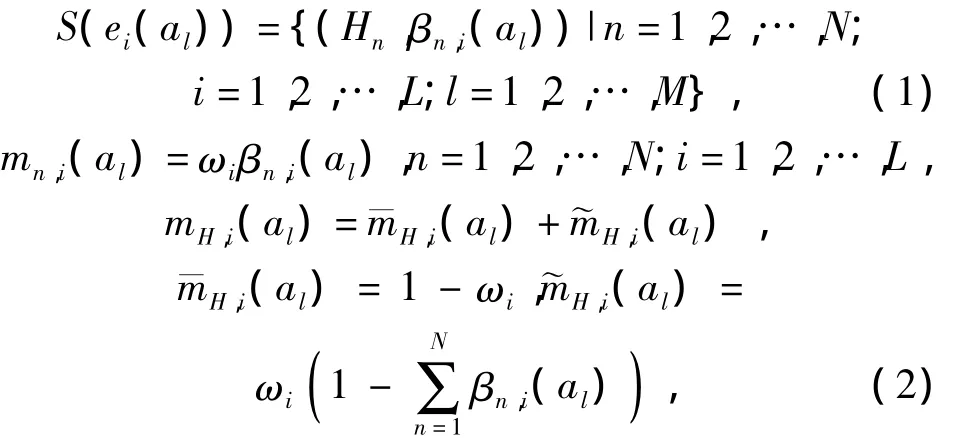
式中:βn,i(al)为方案al在基本属性ei下被评为等级Hn的信任度,βn,i(al)≥ 0 且,当时为完全评价,否则为不完全评价;mH,i(al)为剩余的概率指派函数.
再进行基本概率分配函数的证据集成,如下:

对于∀al∈A,可令.其中,I(i+1)表示集成i+1个基本属性,KI(i+1)为规模化因子,反映了各属性间的冲突程度,即各证据不同时支持某一评价等级的程度.
方案al的上层分布评价如下:
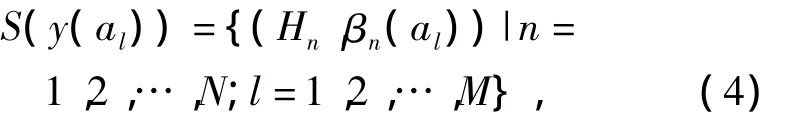
式中S(y(al))表示方案al在上层属性(各备选方案)y下以βn(al)为信任度的等级Hn的分布评价.设等级Hn的效用值为u(Hn),令u(H1)<u(H2)<…<u(HN),则∀al∈A,最大最小平均效用值为
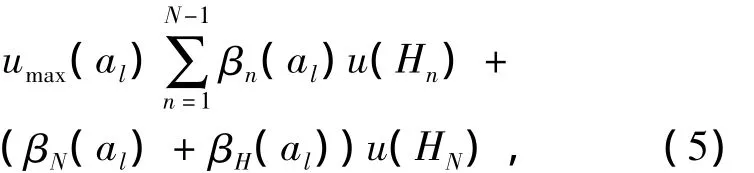

当对方案al做完全评价时,βH(al)=0,显然有umax(al)=umin(al)=uave(al).
最后,根据效用值的高低确定方案的优劣排序.对于∀al∈A,有

式中:“≺”表示“差于”;“~”表示“无差异与”.
2 证据推理决策新方法中的要点
2.1 评价指标的模糊标度
针对概念设计阶段评价指标具有模糊性和预测性的特点,需要将评价指标进行模糊标度,鉴于三角模糊数具有使用简便、易于理解、能很好表达各种模糊变量的特点,文中在对概念设计方案指标值进行标度时采用三角模糊数形式[14].
将三角模糊数表示的指标Ei记为(Ei1,Ei,Ei2),对于数值指标有

式中:β1,β2称为扩增系数,一般取 0.05 ~ 0.30;Ei为不考虑模糊性的第i个指标的实际预测值,Ei1,Ei2采用容差分析中的扩增系数法确定.
对于定性指标,用语言等级确定方案目标属性的满意度,各语言值隶属度函数如图1所示,例如,可将“较好”表示为(0.50,0.67,0.83).
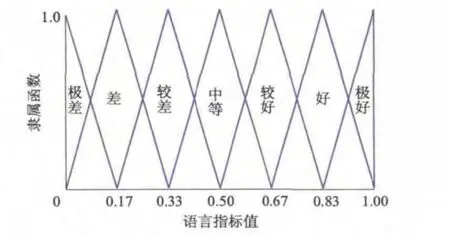
图1 定性指标值的隶属函数
2.2 反偏好权重的确定
文中提出反偏好权重的概念,即采用反偏好函数法确定的属性权重,与Achille Messac教授提出的物理规划法构建偏好函数[15]类似,通过反偏好函数来表达决策者对各设计目标的偏好程度,不同之处在于,文中通过反偏好函数区间即边界值的确定来计算目标属性权重,不是直接利用综合偏好函数进行评价,且在物理规划法中,最终计算出的偏好函数值越小越满意,而文中研究的反偏好权重反映了决策者对各目标属性的重要程度,自然越大越好.
记ei为第i个设计目标,ej,i为区间边界,j=1,2,…,5,nsc为设计目标的数量,则各区间边界上的反偏函数及其一阶导数表示为

例如,对于1R型反偏函数有

2.3 各目标属性值的反偏好函数类型及区间边界
设计目标的反偏好函数,有4种类型:正指标型(1R型),指标越大越好;逆指标型(2R型),指标越小越好;最佳指标型(3R型),指标趋于某值最好;区间指标型(4R型),指标取在某个范围内最好.以目标属性e为横坐标,反偏值作为纵坐标,反偏好函数的定性含义如图2所示.
则方案l在目标属性Ei=(Ei1,Ei,Ei2)上的反偏好函数确定的权值ωi(al)也称反偏权值,可以表示为

式中μ˜Ei(ei)为Ei的隶属函数.则综合反偏好函数值即各目标属性(指标)的权重值ωi可以表示为

这里,0≤ωi≤1,因为权重的确定方法不同于以往传统方法,无需满足.显然,利用反偏好函数来划分重要度区间,在不同的区间范围内,决策者对于此目标属性的重要程度判断是不同的,这符合决策者在多目标属性决策中的思维特点,因此反偏好函数法能够从本质上把握决策者对目标属性的重要度偏好设置.

图2 4种类型的反偏函数
2.4 决策属性评价集的构建
模糊评价集可以依据不同偏好阶段的属性偏重程度来划分,即:

应用证据推理法中针对各评价等级为相应属性区间值的情况确定等级区间.以1R型反偏好区间为例,确定各属性ei对应等级的区间值,如下:应用模糊方法可确定方案al在目标属性ei下的评价信任度为

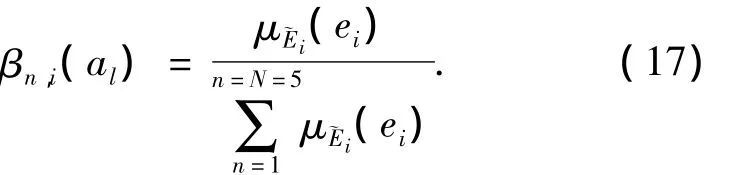
其中μ˜Ei(ei)为Ei的隶属函数,其确定方法见文献[15].
3 实例分析
文中以文献[14]中的应用实例即螺旋输送机输送系统4套初始方案为例进行证据推理决策新方法的应用,确定其有效性,方案如表1所示.
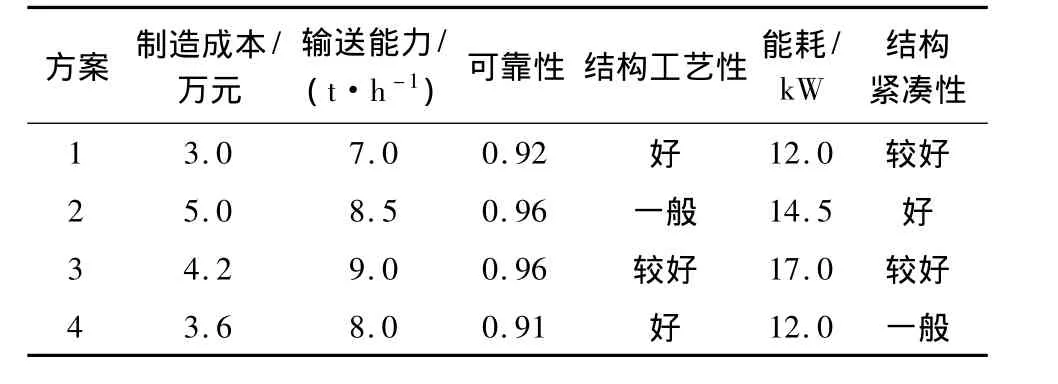
表1 螺旋输送机初始方案指标值
具体步骤如下:
首先,采用模糊标度的方法对备选方案每一目标值进行模糊化处理,结果见表2;
然后,设定各目标属性的反偏好函数类型及等级偏重程度区间边界,本例中,制造成本和能耗的反偏好函数为2R型,其他目标属性为1R型,相应的等级偏重程度区间边界见表3;
最后,根据2.2节的方法,通过反偏好函数法确定决策者对螺旋输送机各评价指标的偏好程度,即偏好权重值.首先,利用公式(11)-(12)确定每个方案目标属性各区间段的反偏函数;然后,通过分段曲线拟合,便可得到符合要求的定量描述的反偏好函数;最后,利用公式(13)-(14)确定各目标属性的权重值,结果见表4.

表2 方案指标的模糊标度

表3 各目标属性的反偏好函数类型及等级区间

表4 各目标属性权重值
应用证据推理算法对属性E={ei|i=1,2,…,5}的指派函数进行证据集成,由公式(16)-(17)确定各评价信任度,则可得方案A={al|l=1,2,…,4}的上层分布评价集:

假设各上层评价等级的效用值分别为u(H1)=0,u(H2)=0.25,u(H3)=0.5,u(H4)=0.75,u(H5)=1,则依据效用值进行方案决策的结果如表5所示.

表5 决策结果
显然,方案优劣排序为a1≺a4≺a2≺a3,文中采用证据推理新决策方法得出的决策值虽与文献[14]的物理规划法决策值含义不同(其最优方案为得分最小值),但排序结果一致,验证了多属性决策方法研究的有效性.
另外,证据推理相比于其他方法的优势在于可以定量描述决策者主观判断上的不确定性和不完全性,本实例中为完全评价;若在决策中,决策者对目标属性的评价把握不准,如本例中,若在设置初始偏好时对于能耗的判断难以估计,将80%的信任度给了中等区间,其他区间不给予评价,即u˜E5(e5)=1,u˜Ei≠5(ei≠5)=0,βn,5(al)=0.8,,则,采用证据推理法得到的决策结果见表6.

表6 不完全决策结果
方案排序为a1≺a4≺a3≺a2,文中假定的情况“将所有方案80%的信任度给了中等区间,其他区间信任度滞空”,相当于决策者“投机取巧”放弃了难以评价的能耗指标,在文献[14]中,方案3原为最优,但出现能耗指标太高不满意的情况,调整偏好后的评价结果与文中的不完全决策结果相同,说明了证据推理法在定量描述决策者主观判断指标不确定性和不完全性上的巧妙之处.
4 结论
1)提出了一种基于反偏好函数的权重确定方法,并采用三角模糊数进行目标属性的模糊标度,通过偏好区间的划分来确定评价等级区间.
2)利用证据推理法中评价等级、概率分配函数、效用值等思想进行了方案的评价决策工作.
3)应用实例验证了所用方法的有效性,并且说明了证据推理法有可以定量描述决策者主观判断上的不确定性和不完全性的优势.
References)
[1]Fan Liguo,Zuo Feng.Research on multi-attribute decision-making method based on AHP and outranking relation[C]∥Proceedings of the2008Workshop on Power Electronics and Intelligent Transportation System.Guangzhou:IEEE Computer Society,2008:227-232.
[2]Vidal L A,Marle F,Bocquet J C.Using a Delphi process and the analytic hierarchy process(AHP)to evaluate the complexity of projects[J].Expert Systems with Applications,2011,38(5):5388-5405.
[3]Mizutani Eiji.A counterexample to a proposed dynamic programming algorithm for optimal bid construction in an auction-based fully distributed manufacturing system[J].International Journal of Advanced Manufacturing Technology,2014,71(1/2/3/4):377-380.
[4]张跃刚,向 号.基于模糊综合评判法的传动方案设计[J].煤矿机械,2007,28(6):36-37.Zhang Yuegang,Xiang Hao.Design of transmission schemes based on fuzzy synthetic evaluation[J].Coal Mine Machinery,2007,28(6):36-37.(in Chinese)
[5]魏锋涛,宋 俐,李 言,等.基于模糊理论的机械多目标优化设计[J].工程图学学报,2010(2):9-12.Wei Fengtao,Song Li,Li Yan,et al.Mechanical multi-object optimization design based on fuzzy theory[J].Journal of Engineering Graphics,2010(2):9-12.(in Chinese)
[6]张 晖,严新平,高 岩,等.基于模糊评价的安全感知与车速相关性分析[J].江苏大学学报:自然科学版,2011,32(5):511-515.Zhang Hui,Yan Xinping,Gao Yan,et al.Relationship between driver safety cognition and vehicle speed based on fuzzy comprehensiveevaluation[J].Journal of Jiangsu University:Natural Science Edition,2011,32(5):511-515.(in Chinese)
[7]Martin H,Spano G,Küster J F,et al.Application and extension of the TOPSIS method for the assessment of floating offshore wind turbine support structures[J].Ships and Offshore Structures,2013,8(5):477-487.
[8]Gruca A,Sikora M.Rule based functional description of genes-estimation of the multicriteria rule interestingness measure by the UTA method[J].Biocybernetics and Biomedical Engineering,2013,33(4):222-234.
[9]邵晓明,安鲁陵,孙小峰,等.一种基于证据推理的机械零件配合设计方法[J].航空制造技术,2010(5):77-80.Shao Xiaoming,An Luling,Sun Xiaofeng,et al.Design method of mechanical part fitting based on evidential reasoning[J].Aeronautical Manufacturing Technology,2010(5):77-80.(in Chinese)
[10]李 磊,裴 凤.基于熵权和证据推理的多属性决策方案评价方法[J].合肥工业大学学报:自然科学版,2010,33(9):1396-1400.Li Lei,Pei Feng.Evaluation method of multi-attribute decision making plans based on entropy weight and evidence reasoning[J].Journal of Hefei University of Technology:Natural Science,2010,33(9):1396-1400.(in Chinese)
[11]郭凯红,李文立.基于证据推理的不确定多属性决策方法[J].管理工程学报,2012,26(2):94-100.Guo Kaihong,Li Wenli.Evidential reasoning-based approach for multiple attribute decision making problems under uncertainty[J].Journal of Industrial Engineering/Engineering Management,2012,26(2):94-100.(in Chinese)
[12]周 谧.基于证据推理的多属性决策中若干问题的研究[D].合肥:合肥工业大学管理学院,2009.
[13]Yang Jianbo.Rule and utility based evidential reasoning approach for multiattribute decision analysis under uncertainties[J].European Journal of Operational Research,2001,131(1):31-61.
[14]薄瑞峰,黄洪钟.交互式模糊物理规划在概念设计方案多目标决策中的应用[J].应用基础与工程科学学报,2005,13(4):442-450.Bo Ruifeng,Huang Hongzhong.Application of interactive fuzzy physical programming in multi-objective decision making for concept selection[J].Journal of Basic Science and Engineering,2005,13(4):442-450.(in Chinese)
[15]Messac A.Physical programming effective optimization for computational design [J].AIAA Journal,1996,34(1):149-158.

