基于新型Gregory三角面片的G1 连续曲面拼接

张华阳，张志毅，杨 龙

（西北农林科技大学 信息工程学院，陕西 杨凌712100）

0 引 言

在逆向工程、电脑动画和地质建模等应用领域中，构造G1连续的光滑曲面是基本要求之一。通过相邻面片间的拼接，在其公共边界每个控制点处有相同的切平面，保证其G1连续［1］。目前最常用的拼接方法：四边域曲面和三角域曲面。郝茹等［2］采用双四次有理Bezier曲面拼接算法来构造G1连续光滑曲面；随后高占恒等［3］采用B样条曲面以及施侃乐等［4］采用周期B样条曲面构造一阶几何连续光滑曲面；R.T.Farouki等［5］采用Coons曲面和Kouichi Konno等［6］采用Gregory面片分别对曲面进行拼接构造光滑曲面，但是他们采用的方法有一定的局限性［7］，不能满足任意的拓扑结构。传统的Gregory三角面片和Bézier三角面片［8］能够自由、灵活地表示任意拓扑结构，但是并不能保证在任意情况下的G1连续。

在本文中，我们采用张志毅［9］提出的新双三次Gregory三角面片对给定的数据进行插值，它不仅满足局部性，而且满足任意三角形［9］或者四边形曲线曲面的拼接并能够达到G1连续。

1 Gregory三角面片

新的Gregory三角面片的几何定义请参考文献 ［10］，其中G 为Gregory三角面片的控制节点或控制网。如图1所示：G 中的每个点称为控制点，例如，｛P0，P1，P2｝为角控制点， ｛P01，P10，P12，P21，P20，P02｝为边界控制点，｛q01，q10，q12，q21，q20，q02｝为内部控制点。所有的控制点可分为3个控制单元。

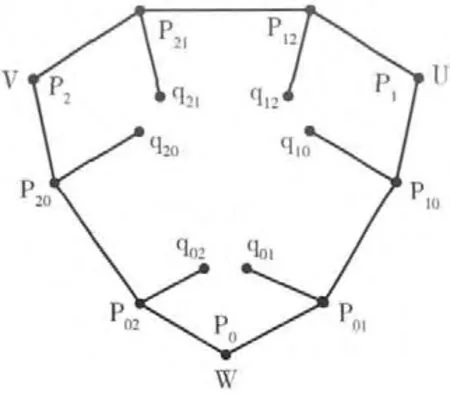
图1 Gregory三角控制网格

在三角面片中，我们用GNT（u，v）表示在这个三角形重心坐标 （u，v）中各个点的位置，那么GNT（u，v）函数可表示为

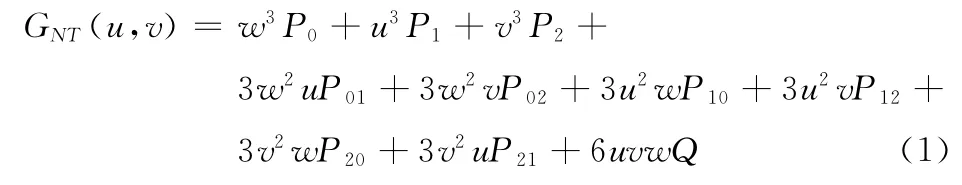
其中u＋v＋w＝1，Q0，Q1，Q2同一个控制单元内一个角控制点相应的2个内部控制点的混合函数，它们表示为

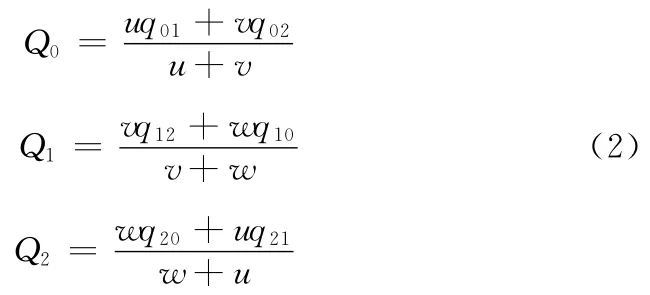
那么Q＝wQ0＋uQ1＋vQ2。

我们利用这种新的Gregory三角面片对给定的数据进行插值，实现G1连续的光滑曲面［9］。

2 G1 连续性条件

一个满足G1连续性条件的曲面具有以下特性：在这个曲面的任意一点，只有唯一一条法线。为了保证全局的G1连续性，我们需要保证2个相邻面片的公共边界能够连续。

相邻Gregory三角面片间的连续性：2个相邻的Gregory三角面片S1和S2如图2所示。2个相邻面片之间的公共边界曲线分别定义了四边界控制点： ｛P0＝P’0，P02＝P’02，P20＝P’20，P2＝P’2｝。

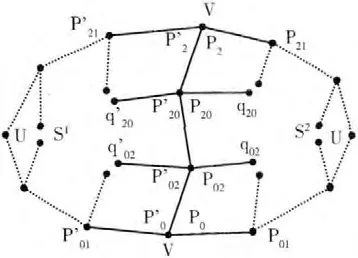
图2 两相邻Gregory三角面片

为了能够更加容易、清楚的对其表述，我们将Gregory三角面片转化为 （u，v）2个变量表达式。用Su表示u 方向的偏导数，Sv表示v方向的偏导数，那么两相邻Gregory三角面片S1和S2满足G1连续的充分必要条件，即方程

要在最严格水资源管理制度试点工作带动下，全面推进最严格水资源管理各项工作，确保各项制度有措施、能落地。一是按照“节水优先、空间均衡、系统治理、两手发力”的治水思路，以水定需，量水而行，因水制宜，严格水资源论证、取水许可管理和水资源有偿使用制度。二是把节约用水贯穿于经济社会发展和群众生活全过程，优化用水结构，切实转变用水方式，全面实行计划用水管理，加快推进节水技术改造。三是全面落实 《全国重要江河湖泊水功能区划》，从严核定水域纳污容量，切实加强水污染防控，加强饮用水水源保护，推进水生态文明建设。四是按照最严格水资源管理制度考核工作要求，积极有序开展辖区内考核工作，切实落实水资源管理责任制。

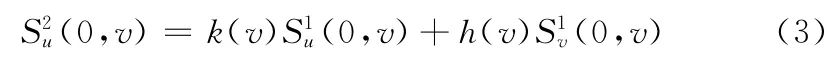
这里，k（v）和h（v）是有关v的标量函数，即公式：

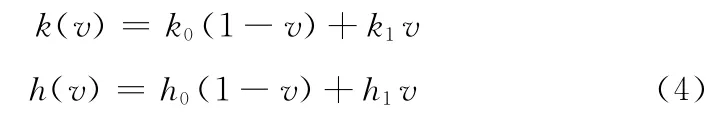
式中：k0，k1，h0，h1——任意实数。

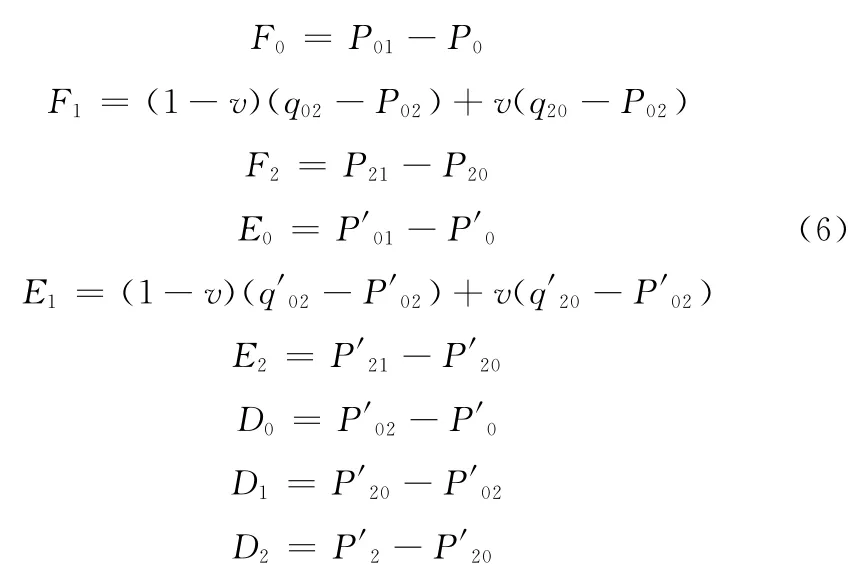
Fj，Ej，Dj称为相邻控制点对的向量组，Fj，Ej为交叉切向量，Dj为公共边界切向量。

对条件方程 （5）进行求解，可得两三角面片间的G1连续性条件，即方程组

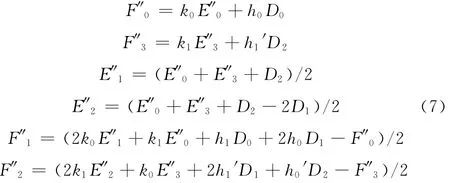
从式 （7）可得到，沿着公共边界的2个相邻三角面片的G1连续是由边界控制点和内部控制点确定的，只是沿着共同的边界曲线通过调整四个内部控制点的位置对2 个Gregory三角面片进行拼接，产生G1连续的光滑表面。

图3表示2个相邻面片的拼接，图中垂直面片的线表示控制点所对应的法线。图3 （a）表示2个面片在公共边界线处具有相同起点的法线不是一致的，导致G1不连续，图3 （b）表示2 个面片在公共边界线处的法线是一致的，G1连续。从扩大部分可见，图3 （a）的曲率等值面与曲面交线是不连续的，而图3 （b）的曲率等值面与曲面交线是连续的。

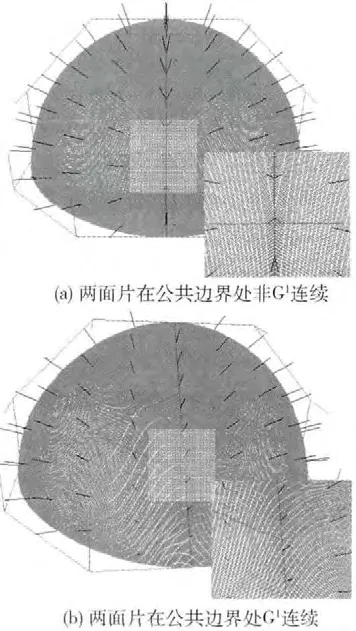
图3 2个相邻三角面片

3 实验结果

由于Gregory三角面片插值方法不能直接用于上述情况，需要预处理原始网格，将基本的三角面片［11］调整为Gregory三角面片，然后使用Gregory三角面片进行插值生成G1光滑曲面的过程［12］，即：①为每一个三角面片的控制顶点生成一个统一的法向量。②为三角面片的每条边界生成边界控制点。③计算每个面片的内部控制点。根据G1连续条件的式 （8），可以计算出相对应的内部控制点。④插值每个Gregory 三角面片控制网格。根据GNT（u，v）（式 （1））中 （u，v）步长的选择，对形体的全局Gregory三角控制网格插值，并构造出G1连续的光滑形体表面。

通过上述介绍的方法对形体曲面的三角形控制网格进行插值，生成G1连续光滑曲面。4个实例形体的G1光滑表面重建结果如图4～图7所示。

图4为cow 的Gregory三角面片的插值过程，■表示角控制点，▲表示边界控制点，●表示内部控制点。图4（a）为相邻两三角面片的原始控制点，图4 （b）为局部两相邻三角面片通过上述的步骤 （2）、步骤 （3）计算获得边界控制点和内部控制点，组成相应的Gregory 三角面片，图4 （c）为全局的控制网格所组成的cow 模型，图4 （d）为插值过后得到的G1光滑曲面。

由于模型中组成三角面片的原始控制点以及通过对原始的三角面片进行预处理得到的Gregory三角面片与cow模型中（a）（b）的相似，图5～图7分别表示其相应的全局控制网格所组成的模型以及插值后得到的光滑曲面结果。

4 结束语

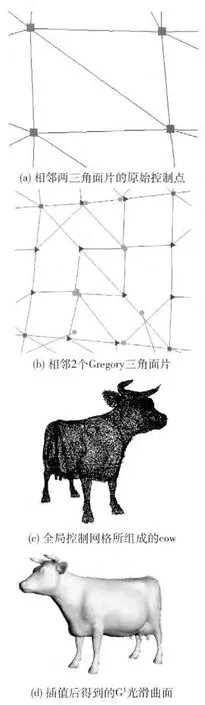
图4 cow 的Gregory三角面片插值过程

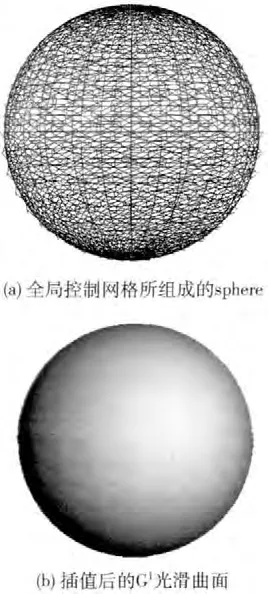
图5 sphere的Gregory三角面片插值

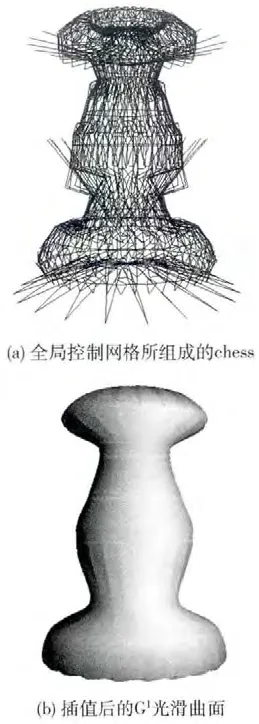
图6 chess的Gregory三角面片插值

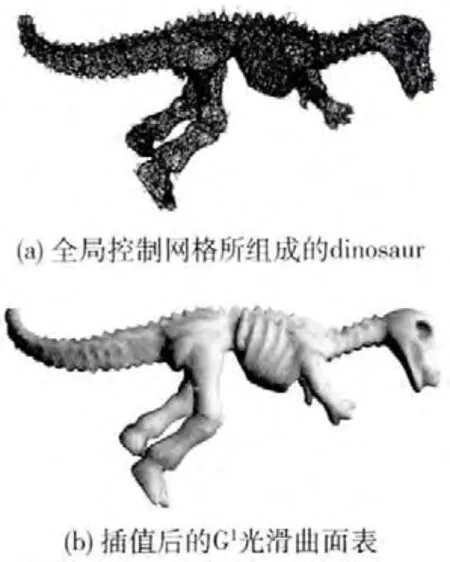
图7 dinosaur的Gregory三角面片插值

Gregory三角面片插值方法为构造光滑连续的形体表面提供了新的途径，随着对三维模型形体设计要求的不断提高，不仅要求光滑甚至要求三维模型形体表面达到一定的光滑标准，因此对形体表面造型技术的基础研究仍然有很大需求。相比传统的Gregory 三角面片，采用新双三次Gregory三角面片插值方法构造G1连续的光滑表面，仅仅通过调整所产生的相邻内部控制点，而没有改变原始的顶点信息。实验结果表明了该插值方法不仅能够重建任意拓扑结构，而且还可以使用原始数据产生令人满意的光滑表面。

今后的研究方向可以生成更加光滑 （二阶几何连续）的三维模型形体表面，从三维模型的形体点云和控制网格以及曲面的高阶几何连续拼接条件为前提，对生成高质量的形体曲面做更加深入的研究。

［1］Farin G.Curves and surfaces for computer aided geometric de－sign：A practical guide ［M］4th ed.New York：Academic Press，1997：64－306.

［2］HAO RU，LIU Runtao.Joining between adjacent rational Bezier surfaces ［J］.Computer Engineering and Application，2010，46 （4）：174－175 （in Chinese）. ［郝茹，刘润涛.双四次有理Bezier曲面G1光滑拼接算法 ［J］.计算机工程与应用，2010，46 （4）：174－175.］

［3］GAO Zhanheng，LIANG Xuezhang，GAO Fushun，et al.Research on G1continuity conditons between B－spline surfaces and construction of local scheme ［J］.Journal of Computer－Aided Design ＆ Computer Graphics，2007，19 （7）：866－870 （in Chinese）.［高占恒，梁学章，高福顺，等.B 样条曲面间G1连续条件及局部格式构造问题 ［J］.计算机辅助设计与图形学学报，2007，19 （7）：866－870.］

［4］SHI Kanle，YONG Junhai，SUN Jiaguang，et al.Gnfilling orbicular N－sidede holes using periodic B－spline surfaces ［J］.Science China：Information Science，2011，41 （9）：1112－1125 （in Chinese）. ［施侃乐，雍俊海，孙家广.基于周期B样条曲面的环状N 边洞Gn连续性过渡 ［J］.中国科学：信息科学，2011，41 （9）：1112－1125.］

［5］Farouki RT，Szafran N，Biard L.Construction and smoothing of triangular coons patches with geodesic boundary curves［J］.Computer Aided Geometric Desgin，2010，27 （4）：301－312.

［6］Kouichi Konno，Hiroaki Chiykura.An approach of designing and controlling free－form surfaces by using NURBS boundary Gregory patches ［J］.Computer Aided Geometric Design，1996，13 （9）：825－849.

［7］ZHU Xinxiong.The modeling technology of free－form curve and surface ［M］.Beijing：Science Press，2000：198－232 （in Chinese）.［朱心雄.自由曲线曲面造型技术 ［M］，北京：科学出版社，2000：198－212.］

［8］ZHANG Lei，WANG Guo－jin.Computation of lower derivatives of rational triangular Bezier surfaces and their bounds estimation ［J］.Journal of Zhejiang University Science，2005，6（1）：108－115.

［9］Barnhill R E，Gregory J A.Compatible Smooth Interpolation in Triangles［J］.Journal of Approximation Theory，1975，15（3）：214－225.

［10］Zhang Zhiyi，Wang Zhenhua，He Dongjian.A New Bi－cubic Triangular Gregory Patch［C］／／Proceedings of the 2008International Conference on Computer Science and Software Engineering.Wu－Han：IEEE Computer Society Press，2008：1003－1007.

［11］Hans Hagen，Gregory Nielson，Yasuo Nakajima.Surface design using triangular patches［J］.Computer Aided Geometric Design，1996，13 （9）：895－904.

［12］Long Yang，Dongjia He，ZhiyiZhang，Construction of G1smooth surface employing triangular Gregory Patches［C］／／Proceedings of the 5th International Conference on Image and Graphics.Xi’an：IEEE Computer Society Press，2009：577－580.