VEI规模、偏好与科技型中小企业分享机理

孔令夷

（西安邮电大学 经济与管理学院，陕西西安 710061）

一、引言

创业股权投资（Venture Equity Investment，VEI）特指投资公司或企业以收购科技型中小创业企业股权为形式的投资。①Thomas Anderson，Glenda Napier，The Role of Venture Capital：Global Trends and Issues from a Nordic Perspective.Malmö：International Organization for Knowledge Economy and Enterprise Development，2005，PP.1-104.据悉，上世纪60-70年代，全球500 强的四分之一都从事着VEI 活动。②Gompers P，Lerner J，The Determinants of Corporate Venture Capital Success： Organizational Structure， Incentives and Complementarities.Cambridge，MA：NBER Working Paper No.6725，1998，PP.1-49.科技市场竞争强度的加剧使得企业研发活动外部性成为常态，而科技型中小企业具有强烈的融资需求和旺盛的创新力，因此更多从事高新技术的企业涌入VEI，将其作为外部创新渠道之一。VEI 不仅具有传统投资的回报功效，更能满足企业创新战略的需要①Deloitte，Global Trends in Venture Capital 2009 Global Report.http：//www.deloitte.com，2009.，有证据显示还能带动投资方实施多元化运营②Ernst ＆ Young，Corporate Venture Capital Report.http：//www.ey.com，2002.、独立创新。③Dushnitsky G，Lenox M J，“When do Incumbents Learn from Entrepreneurial Ventures？ Corporate Venture Capital and Investing Firm Innovation Rates”，Research Policy，Vol.34，No.5，2005，PP.615-639.

另一方面，对于科技型中小企业而言，VEI 对于其成功创业是举足轻重的。④Allen D，Gorham J，Peake T，“Small Business Incubators-phases of Development and the Management Challenge”，Economic Development Commentary，Vol.2，No.2，1987，PP.6-11.在科技型中小企业创业过程中，风险大、投入及回报多、成长快，最突出的资源瓶颈就是有限资金。⑤Smilor R W，Gill M D，The New Business Incubator：Linking Talent， Technology， Capital， and Know －how.Kentucky：Lexington Books，1986，PP.87-91.因此，科技型中小企业与创投机构联手必然是解决其最大创业瓶颈的首选路径。然而，近年来多项国际性调查发现二者的融合仍不理想⑥Al-Mubaraki H M，Busler M，“Business Incubators：Findings from a Worldwide Survey，and Guidance for the GCC States”，Global Business Review，Vol.11，No.1，2010，PP.1-30.，国内VEI 也存在不少桎梏，包括官办色彩浓厚、科技型创业企业信誉度低、VEI 管理制度不健全等。⑦卢珊、赵黎明：《基于协同理论的创业投资机构与科技型中小企业演化博弈分析》，《科学学与科学技术管理》2011年第7 期。

股权交易价格始终是创投机构与科技型中小企业的关注焦点。虽然核定成交价的方法不少，比如有股价收益比率法、股票期权计划等，但是解释股权交易价格产生机制、演化路径的文献却很少。实际上，股权交易价格产生机制的重要性远远超出估价方法，因为它不但可以反映VEI 的不完全动态信息，而且有助于深入探析被投资股权的真正市场价值，高效配置资金与技术等关键资源，优化投资效率，实质性提升创业企业的创新绩效。

竞标是一种科学高效的交易方式，适用于不完全信息条件下的复杂性股权投融资，为资金流动及技术创新提供了理想的实现平台，有利于确定被投资股权的实际市场价值。到底怎样分析VEI 竞标中极为重要的交易价格产生机制？博弈论以其关注个体或群体间交互作用、反应及影响而著称，以彼此间对抗、依赖和制约为研究前提和出发点，在大规模、更集中的、强对抗或深度合作问题研究方面发挥了积极而不可替代的作用。⑧谢识予：《经济博弈论》，复旦大学出版社2006年版，第233-275 页。而有限理性假设下的演化博弈论可能更适合于分析VEI 竞标及中小企业分享VEI 问题。⑨Mengel F，“Conformism and Cooperation in a Local Interaction Model”，Journal of Evolutionary Economics，Vol.19，No.3，2009，PP.397-415.本文拟探析不同VEI 规模及偏好下科技型中小企业的竞标策略交互影响及其要因，设计竞标激励条件以加强创投中创业企业竞合性及其对VEI 的合理分享。

二、VEI竞标的演化博弈模型分析

（一）理论假设

（1）首先约定本文研究的是进行VEI 的一个创投企业和接受投资的两个科技型中小企业。创投企业在VEI 中计划投资或购买股权数为I，而两家科技型中小企业的股权规模不同，即引资能力不同，令W1为实力较强、对VEI 吸收资金能力较强的中小企业1，总股权数I1；令W2为对VEI 吸收能力较弱的中小企业2，总股权数I2，可知I1> I2。

（2）假设两家科技型中小企业的投资价值是无差异、可替代的。它们对各自股权的单股评估价值分别为V1和V2，二者具有独立性，且服从同类统计分布。

（3）VEI 竞标中两家科技型中小企业互为竞争对手，既想要中标，又希望获利。作为第三个局中人的创投企业是VEI 招标方，有权确定股权投标方的可选价格。创投企业要求并告知两家科技型中小企业：可以选择且只能选择一个高价格和一个低价格出让各自股权，高价为h，低价为l，因此竞标博弈局中人的竞标价格决策就是选择h 或l。

（4）本文只讨论VEI 下的合资经营行为，即创投企业与科技型中小企业组建合资企业，而不考虑创投企业全资收购中小企业的独资化情形。假定创投企业的股权比例不能超出49%，两家科技型中小企业的引资能力足够大，能确保实现VEI 市场的出清，创投企业投资股权（份）数量I不大于两家科技型中小企业股权数之和Is的49%，即I≤0.49（I1+I2）=0.49Is。

（5）作为第三个局中人的创投企业是股权购买方，也有权确定招投标规则，其中极为重要的就是对竞标方的优选偏好，优先级依次降低。

第一偏好：价格最低化。创投企业在VEI 过程中，首选竞标价格低者的股权进行投资。

第二偏好，管理及治理成本最小化。买入中小企业股权后创投企业需要参与合资企业的管理，包括派驻管理者、研发投入、科技资源共享、运营资金支持和人员培训等，必然会增大创投企业的管理及治理成本。因此，本文假定，在同等价格条件下，如果买入一家科技型中小企业的股权就能够满足创投企业的VEI 计划数，则不考虑买入两家中小企业的股权。

第三偏好：总控制权最大化。创投企业在选择投标方的情境中，总是希望对所有科技型中小企业的总控股权最大，以求得到它在合资企业经营管理及技术研发中最大的控制权及话语权。如果创投企业必须同时买入两家科技型中小企业的股权，才能够满足VEI 计划数，为了加强对技术扩散和合资企业经营管理的控制，创投企业对两家科技型中小企业的VEI 数量分配决策将以总股权比例最大化作为投资偏好。

（6）两家科技型中小企业归属于两类群体参与者（生物种群），它们的理性程度是有限的，在竞标的反复博弈中，也即两类种群的相互观察、学习和调整适应过程中，学习速度较慢，报价策略调整用生物进化的“复制动态”机制模拟。

（二）模型构建

给出两家科技型中小企业在竞标中不同股权报价形成支付的矩阵（表1）。

表1 两家科技型中小企业在VEI竞标中支付矩阵的一般形式

设W1报价h 的概率p1用x 指代，W2报价h的概率p2用y 指代，那么VEI 竞标过程中双方策略类型比例变化复制动态的关系，在以两个比例为横纵坐标轴的正方平面图上可以表示出来。任一时刻两家科技型中小企业局中人的交互情况为：P=［（p1，1-p1），（p2，1-p2）］＝［（x，1-x），（y，1-y）］，这都可用图中的对应点（x，y）来描述。企业W1报价h 的期望得益为π1h=yπ1hh+（1-y）π1hl，报价l 的期望得益为π1l=yπ1lh+（1-y）π1ll，故W1的平均得益为π1=xπ1h+（1-x）π1l；同样地，W2报价h 的期望得益为π2h=xπ2hh+（1-x）π2lh，报价l 的期望得益为π2l=xπ2hl+（1-x）π2ll，故企业W2的平均期望得益为π2=yπ2h+（1-y）π2l。据演化博弈的复制动态机理，两家科技型中小企业竞标价格策略动态变化速度可用微分方程表示为：

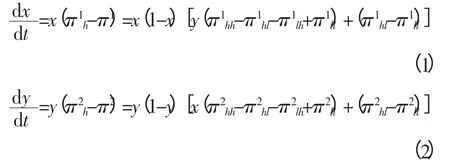
易算出该VEI 竞标演化博弈的均衡解（点）有5 个：A（0，0），B（1，0），C（0，1），D（1，1），E若要判断这些均衡点的演化稳定性，应借助方程（1）及（2）的Jacobian 矩阵J：

判断法则是：与均衡点取值相应的矩阵J 的行列式Det（J）大于0，且行列式的迹Tr（J）小于0，则该均衡点为ESS；若迹等于0，则为鞍点。显然两家科技型中小企业在各种情形下的收益不同，就会产生不同的ESS 和鞍点。

三、演化博弈均衡分析

结合本文的VEI 规模及内资出让股权数的数值比较，分为三种不同条件来分析两家科技型中小企业的博弈支付矩阵及相应的均衡点性态。

（一）投资股权数小于W2 的最大出让股权数

基于创投企业对投标方优选的管理及治理成本最小化偏好，此时任何一家科技型中小企业都能满足创投企业的VEI 计划数I，不能同时买入两家科技型中小企业的股权。进一步地，到底买前者还是后者？根据总控制权最大化偏好，由于企业2 的总股权基数较小，当然选择其更优。表1转换为表2的具体形式，此博弈矩阵无稳定均衡点。

表2 当0＜I≤0.49I2 时两家科技型中小企业的支付矩阵

（二）投资股权数处于两家科技型中小企业最大出让股权数的中间

基于第二条偏好，只有企业W1才能满足创投企业的VEI 计划数I，那么在同等竞标价格条件下，创投企业应该只买入东道国企业W1的股权，见表3：

表3 当0.49I2＜I≤0.49I1 时两家科技型中小企业的支付矩阵

如果π1hl＞π1ll，即中小企业W1选择高价h，均衡点为B（1，0）；反之，如果π1hl＜π1ll，即无稳定均衡点，但是中小企业W2的占优策略是低价。

（三）投资股权数大于科技型中小企业W1的最大出让股权数

创投企业必须同时买入企业1 及企业2 的股权；到底先全部买入企业1 的49%股权再买入小企业的股权还是相反顺序？如果创投企业先全部买入W1的49%股权再买入W2的股权，那么总控股权比例为，如果先全部买入W2的49%股权再买入W1的股权，那么总控股权比例，两种相反的投资顺序的创投企业总控股权比例之差：

综上，在同等竞标价格条件下，先全部买入W2的49%股权，再买入W1的部分股权，以满足剩余的VEI 计划数。此种情形下，表1变换为表4。

为了对支付矩阵归类为不同条件下的演化均衡分析，拟借鉴稳定性定理。①孙庆文、陆柳、严广乐、车宏安：《不完全信息条件下演化博弈均衡的稳定性分析》，《系统工程理论与实践》2003年第7期。

（1）如果π1hh＞π1lh，即该复制动态系统具有4 个均衡点A ～D，仅D（1，1）是ESS，一并分析各个均衡点的演化稳定性，如表5所示。

此情形下的非对称博弈中，两家科技型中小企业群体通过复制动态学习及策略调整演化，最终的稳定均衡状态是双方都会采取高价竞标。W2以最大限度出让其总股权数的49%，即0.49I2；W1出让剩余股权数，即I-0.49I2，以满足创投企业的VEI 计划。

表4 当0.49I1＜I≤0.49Is 时两家科技型中小企业的支付矩阵

表5 π1hh>π1lh 条件下各均衡点的演化稳定性

（2）如果π1hh＜π1lh且π2lh＞π2ll，即该复制动态系统具有4 个均衡点A～D，仅C（0，1）是ESS，如表6所示。

非对称博弈中，两类科技型中小企业群体通过复制动态学习及策略调整，演化到稳定均衡状态为企业1 采取低价竞标，企业2 采取高价竞标。W1以最大限度出让其总股权数的49%（0.49I1）；W2出让剩余股权数（I-0.49I1），以满足创投企业的VEI 计划。

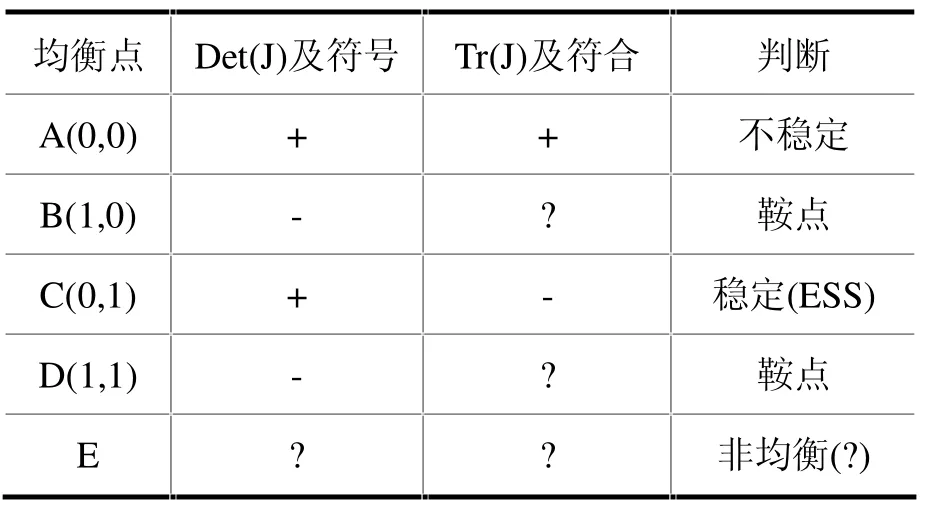
表6 π1hh＜π1lh 且π2lh＞π2ll 条件下各均衡点的演化稳定性

根据博弈论的箭头法，也可验证出该情境下的相对稳定性策略是C（0，1）。不妨先从（高价，低价）开始，那么局中人1 会单独改变策略以增加得益，使策略组合变为（低价，低价），接着，局中人2 也会单独改变竞价策略以获得更多收益，使策略组合变为（低价，高价），此时哪一方单独改变竞价策略都是不划算的，因此C（0，1）是稳定的策略组合；如果局中人2 先改变，接着局中人1 再改变，结果也是如此，不再赘述。

（3）如果π1hh＜π1lh且π2lh＜π2ll，即V1）+V1且具有5 个均衡点A～E，均不具有演化稳定性，没有ESS。A～D 是鞍点，如表7所示。

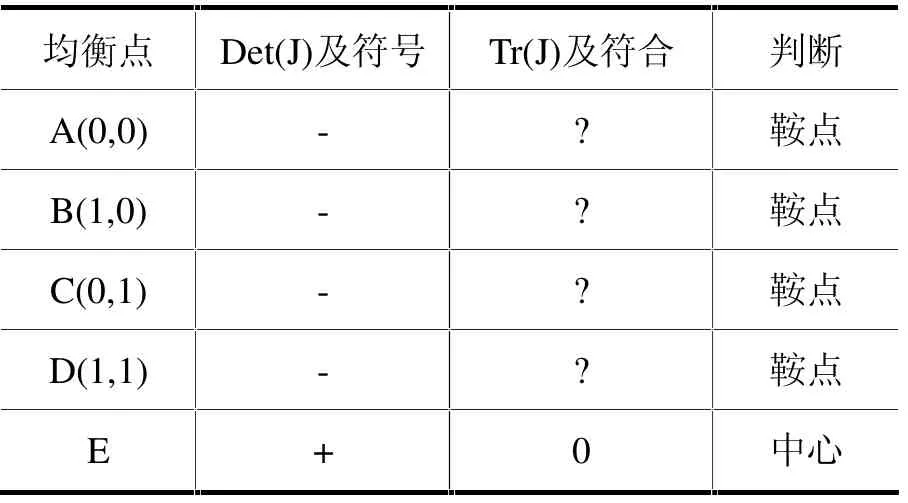
表7 π1hh＜π1lh 且π2lh＞π2ll 条件下各均衡点的演化稳定性

此情形下的非对称博弈中，两家科技型中小企业群体通过复制动态学习及策略调整，双方不会稳定于任何竞标策略。大多数情形下，W2以最大限度出让其总股权数的49%，即0.49I2；W1出让剩余股权数，即I-0.49I2，以满足创投企业的VEI 计划，这会发生于A（0，0）、B（1，0） 及D（1，1）三个均衡点。但是，也有可能出现：W1以最大限度出让其总股权数的49%，即0.49I1；W2出让剩余股权数，即I-0.49I1，以满足创投企业的VEI 计划，这仅仅发生于企业2 报高价且企业1报低价的策略组合的时候，即均衡点C（0，1）。

该非对称博弈的两群体复制动态关系是不确定的，A（0，0）、B（1，0）、C（0，1）与D（1，1）4 个均衡点在演化过程中的性态都是鞍点，E为中心，没有ESS，即两家科技型中小企业在交互影响下不会稳定于纯策略均衡点，两家科技型中小企业的竞标策略围绕着四个纯策略均衡点往复调整变化，围绕着均衡点E 作圆周运动。

（四）演化博弈均衡的影响参数分析

上述三种情形下支付矩阵决定了截然不同的竞标策略转变渐进过程及演化系统各均衡点的稳定性，也就是说，两家科技型中小企业得益的比较关系是竞标博弈均衡情况差异化的充分条件。创投企业作为VEI 招标者，期望两家科技型中小企业都提供低价的股权，即实现最优均衡点A（0，0）的稳定收敛性，以此确保创投企业的最大得益。

（1）创投企业投资股权数I 对竞标系统收敛性的影响

对比前文三种情形下两个博弈方竞价策略渐进稳定于同时报出低价的A（0，0）的条件概率大小，倒序排列后依次为：0＜I≤0.49I2，0.49I2＜I≤0.49I1，0.49I1＜I≤0.49Is。不难发现，当各竞标方的规模更大、吸收能力更强、总股本数更多或最大出让股权数更多，更能够独立满足创投企业的VEI 需求时，就更倾向于以低价出让股权，竞标系统更倾向于向最优均衡态渐变；反之则可能陷入不理想的竞标格局，投标方都报出高价。或者，从另一面的创投企业来说，VEI 计划数越小越有利，就越能以最低成本实现对中小企业的最大控制权。

（2）竞标报价h 以及l 对竞标系统收敛性的影响

在前文3.2 的情形（0.49I2＜I≤0.49I1）中，如果均衡点为B（1，0）；反之，如果h＜无稳定均衡点，但是中小企业2的占优策略是低价。可以看出，双方竞标报价策略向低价渐变的概率随着增大l、减少h 而增大。

再看3.3 的情形（0.49I1＜I≤0.49Is）中的演化稳定性，如果（1，1）是ESS；如果V1，C（0，1）是ESS；如果且是鞍点，E 是中心。可见，随着增大l、减少h，双方竞标报价策略向A（0，0）渐变的概率会增大，收敛于VEI 竞标系统的理想均衡点（低价，低价），即A（0，0）的速度会趋于加快。

总之，无论何种情形，双方竞标报价策略向低价渐变的概率随着增大l、减少h 而增大。

（3）竞标方的股权估价V1、V2对竞标系统收敛性的影响

在3.2 的情形（0.49I2＜I≤0.49I1）中，如果π1hl＞π1ll，即，均衡点为B（1，0）；反之，如果π1hl＜π1ll，即，无稳定均衡点。

再看3.3 的情形（0.49I1＜I≤0.49Is），如果π1hh＞π1lh，即，则有D（1，1）是ESS；如果π1hh＜π1lh且π2h＞π2ll， 即 V1＜且，仅C（0，1）是ESS；再如果有且，A～D 是鞍点，E 是中心。

减少V1、增大V2总促使竞标方低价选择的比例向更大数值变化，竞价策略组合向A（0，0）或C（0，1）的低价竞标均衡渐变演化的概率增大，W1的低价选择比例将达到1，x 趋于0。

当VEI 的投资强度较低，创投规模较小（0.49I2＜I≤0.49I1） 的情况下，VEI 显得稀缺而难得，科技型中小企业估价水平对于中标起到决定性作用，科技型中小企业会竭力争取出让股权而换取投资，以提升其创新能力。为了获取竞标系统的最佳均衡A（0，0），W1会有意识地放低股权估价V1，也就增大了引入VEI 的积极性以及低价竞标的激励性。然而，V2对于竞标系统稳定性无关，主要是源于本文的理论假设中第五条的竞标方优选偏好二，即VEI 的投资对象企业数量最小化的限制，创投企业为了降低其对合资企业的管理及治理成本，偏好于只投资W1，优先考虑只购买企业W1的股权，而非同时购买两家企业的股权。

当VEI 的投资强度较高，创投规模较大的情况下，即0.49I1＜I≤0.49Is时，虽然无法取得复制动态竞标系统的最理想均衡A（0，0），但是减少V1也能促使A（0，0）成为鞍点。

而且，在0.49I1＜I≤0.49Is条件下，减少V1的同时增大V2，有利于向C（0，1）收敛，形成ESS。此时，创投企业更渴望获取中小企业股权，两家科技型中小企业引资的可能性提高，投资竞标的竞争不会过于激烈，未必会形成双方同时低价竞标的局面。为了获取竞标系统的最佳均衡，W1主动减少V1，缩小与W2的股权估价差距，提高自身的单股收益及预期收益，为自己选择低竞价做好铺垫，谋求“薄利多销”模式下的更大规模注资，实现总收益最大。此时，企业1 的种群在竞标中选择低价策略的可能性渐增，从而兼顾中标机会及得益大小，赢得投标主动权和外商注资优先权，尽最大可能首先中标，促使创投企业先购入W1的最大股权出让数（即0.49I1），充分利用VEI提升自身技术水平及创新能力。

总之，随着较强内资竞标方的股权估价V1逐渐减小，该企业越有可能在竞标中报出低价，这对创投企业的VEI 很有利，当然也利于中小企业快速获取创投资金。正如C（0，1）的竞标行为演化均衡结果，既能满足招标方的投资需求和战略取向，也能满足实力较强的中小企业投标方的战略性融资需求。

然而，吸收能力弱的科技型中小企业应估价较高为宜，以主动降低单股收益，这也与创投企业选购一家股权优于选购两家股权的投资策略有关。W2有意识地选择高价竞标，可以与W1在竞标中拉开差距，避免竞标中的恶性价格竞争。作为行业跟随者，较弱的W2只需要有限地引入资金即可，量力而行且有限地提升自身技术水平及创新能力。所谓“有限的”意指：科技型中小企业W2对自身股权作出较高估价，就更有可能以高价竞标，从而ESS 趋向C（0，1），在此演化稳定均衡条件下，W2的资金引入量小于双方同时低价竞标的A（0，0）均衡点条件下该企业的资金引入量，即I-0.49I1＜0.49I2。

四、数值仿真实验

通过提供实际VEI 竞标的相关数值，测度x0、y0、I、h、l、V1以及V2对演化博弈均衡态势的影响，并结合影响行为演化稳定的因素分析及数值仿真实验，拟作出面向最优均衡状况的政策设计，以及给出博弈方招投标对策建议。设定VEI计划数I 为100 万股，W1的总股权数I1为240 万股，W2的总股权数I2 为160 万股；V1为6 元/股，V2为4 元/股。根据布莱克－肖莱斯期权定价模型①何良桥：《评西方期权定价理论》，《世界经济》1994年第12期。，两家科技型中小企业股权估价都服从于对数正态分布（4，0.05），竞标价格h 为12 元/股，l 为7 元/股。②孙竹：《西方资产定价理论中的实体经济因素考察——以CAPM模型与B-S期权定价模型为例》，《中央财经大学学报》2007年第2期。那么，0.49I2＜I≤0.49I1成立，局中人支付为：（π1hh，π2hh）=（600，0），π1hl，π2hl=（129.6，235.2），π1lh，π2lh=（100，0），π1ll，π2ll=（100，0）。而且，该算例满足因此均衡点为B（1，0）。

（一）初始比例x 和y 对博弈均衡的影响

令W1的高股价选择初始比例x0分别取值为0.1、0.4、0.6 及0.9。W2的高股价选择初始比例y0无论取值0.2 还是0.8，都会得出图1的演化曲线，与理论分析3.2 的结果一致的是该情境出现稳定的演化均衡点B（1，0）。在本算例中，创投企业的VEI 计划数介于两家中小企业的最大出让股权数之间，因此，对于VEI 的创投企业而言，必然偏好于只购入W1的股权；而W1明晓这一事实，因此该企业主动提高竞标价格以期望获得更大的股权出让收益。W1和W2分别以高价与低价出让各自股权，实现稳定均衡，达到了各方在招投标中的最大满意度，B（1，0）的均衡格局既满足了创投企业意欲降低管理难度的目标取向与利益追求，同时也使W1获取较高的股权交易回报。图1清晰地显示出W1在竞标过程中的竞价策略演化过程，也间接地揭示了创投企业与科技型中小企业彼此之间的竞争性与依赖交互关系。图1中向稳定均衡点B（1，0）的收敛进程有长短、快慢之分，这与初始比例x0密切相关，初始值越接近稳定态均衡点，收敛越快。然而演化速度与y的初始值无关。这源于当创投企业投资计划数介于两个竞标方的最大出让股权数时，创投企业不考虑购入W2的股权，因此W2的竞标价对于VEI股权竞标演化稳定没有影响，无论其初始选择比例高低与否。

在竞标起始点，作为博弈方的W1的报高价者初始比例x0越大，其竞价策略越可能向最终均衡点B（1，0）演化，演化速度越快。再比较图1中W2的报高价者初始比例y0是0.2 和0.8，能发现当0.49I2＜I≤0.49I1时，W1的竞价策略演化方向和速度只与自身种群的竞价选择初始比例有关联，不会受到W2的竞价选择初始比例y0的影响。因此，作为招标方的创投企业的正面引导、声明发布等信息传递方式，以及激励较强的W1适当降低竞标价的相应举措，都能够在一定程度上改变科技型中小企业竞价选择行为的初始比例值，进一步推动博弈方朝着预期的理想均衡快速有效演化。政府在招商引资政绩压力下，应积极配合创投企业加强竞价监管，倡导及鼓励适价或低价竞标，杜绝中小企业私下勾结或恶意哄抬股权出让价等，为VEI 提供有利的市场环境，也能加速技术进步，实现投融资方的双赢。

（二）VEI 计划数I 对演化过程的影响

保持y0为0.2，使I 减少到90 万股，仍然满足0.49I2＜I≤0.49I1，得到图2（1）的竞标行为演化情形。对比图1与图2（1）发现，当创投企业计划投资股权数减少，竞标均衡B（1，0）转变为不稳定均衡，企业1 的高价出让股权策略最终演化为在低价与高价之间震荡，竞标系统有向最优化均衡A（0，0）靠拢及演化的趋势。

再保持y0为0.2，使I 增加到120 万股，此时有0.49I1＜I≤0.49Is成立，而且有π1hh＞π1lh成立，则有D（1，1）是ESS，得到图2（2）的竞标行为演化情形。对比图1及图2（2），发现随着投资数I 增加，更易落入不理想的双方出高价投标的ESS，即D（1，1），导致挫伤创投企业VEI 积极性。为了加速技术创新和创业扶持，固然应加大VEI 力度，然而VEI 并不是单次投资越多越有利，应依据实情而拿捏好投资的合理尺度及强度。VEI 计划数I，若能改变大量少次投资为少量多次投资，每次投资数不超过科技型中小企业股权数较少者的最大股权出让数，更会实现创业企业低价竞标的理想均衡。同时给创投企业和政府的启发是：保密VEI 数更能刺激科技型中小企业在竞标中让利，加强竞标方引资的股权价格竞争性。

（三）竞标价h 和l 对演化过程的影响

图2 创投企业VEI 计划数I 对VEI 分享演化稳定过程的影响

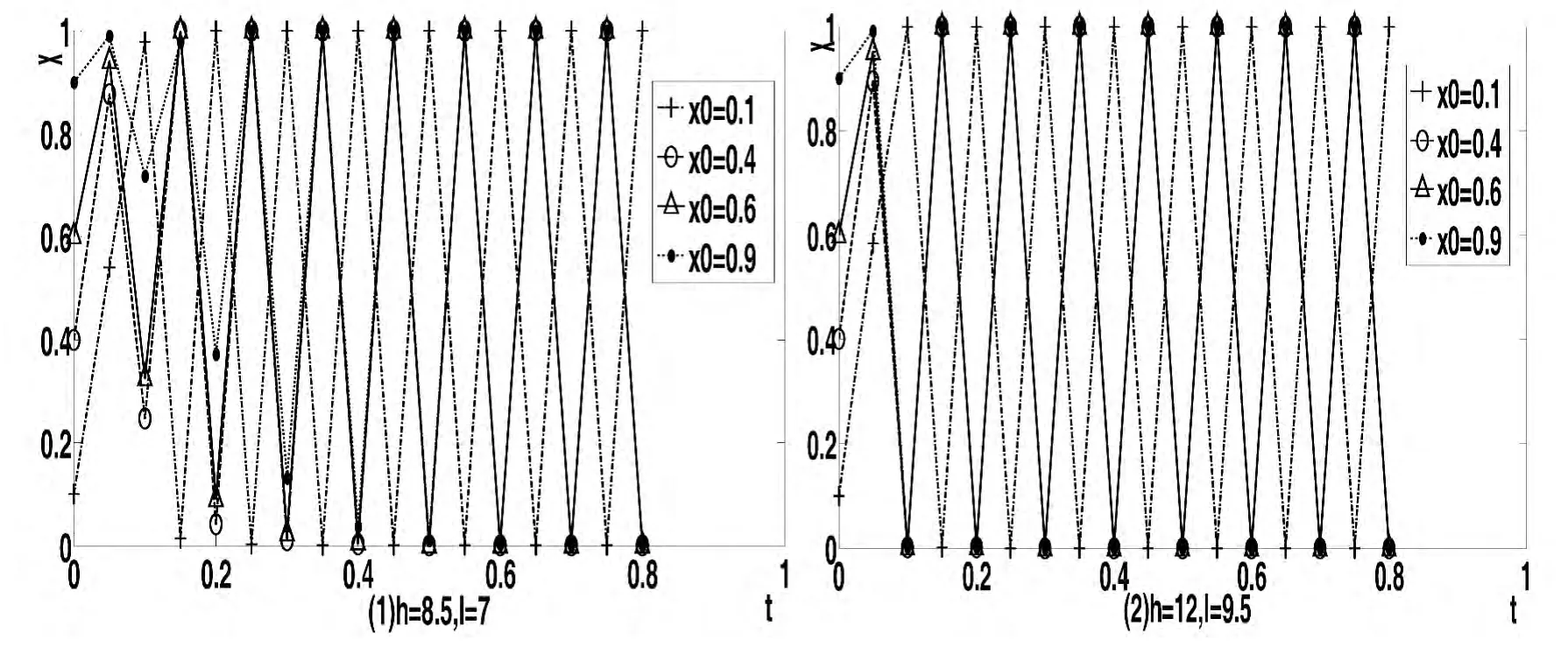
图3 博弈方竞价上限h、底限l 对VEI 分享演化稳定过程的影响

保持y0为0.2，I 为120 万股，先引入投标价上限h 为8.5 元/股，得到图3（1）的竞标行为演化情形；再保持h 为12 元/股不变动，改变竞标低价l，设置竞标价底限为9.5 元/股，得到图3（2）的竞标行为演化情形。对比图2（2）与图3，可见，减少h，设置竞价上限低于两家科技型中小企业原先报出的高股价；同时提高l，竞价底限设置应高于两家科技型中小企业原先报出的低股价，不但能使得科技型中小企业竞标交互行为发生改变，竞价在高低价之间往复震荡，有机会达到较为理想的低价竞标均衡点，有利于向VEI 竞标系统最优均衡的低价竞标状态逐渐靠拢，避免各竞标方同时标出高价的不利状况。原因在于价格上限克制了竞标方不当牟利，价格下限又能增加中小企业的股权出让补偿，如此公道合理的竞标规则设置必能驱使甚至激励竞标方以积极姿态出让各自股权，以低股价策略吸引并换取投资。总之，缩小竞标企业报价区间，有利于VEI 的综合效应。

（四）科技型中小企业股权估价V1 和V2 对竞标价选择行为调整过程的影响

对照图1，仍然取值y0为0.2，I 为100 万股，h 为12 元/股，l 为7 元/股，V1减少为5.5 元/股，V2仍保持为4 元/股，其余参数保持不变动，得到图4（1）的竞标行为演化情形。因本算例符合0.49I2＜I≤0.49I1，随着V1减少，竞标博弈方报价选择比例已不是向原先的ESS（即B（1，0））渐变，而转向不稳定均衡，一定程度上向着有利于VEI的“低价竞标”方向变化演进。对于企业1 而言，竞标结果震荡于高低竞标股价交易的可变情境（图4（1））；对于中小企业2，则震荡于低股价竞标与初始选择高股价竞标的子种群比例之间，即y 震荡于0 与初始选择高股价竞标的子种群比例之间。因此，当VEI 规模有限而稀缺时，企业1 的理性选择是降低估价，积极争取投资，低估价对于低价竞标起到正向作用，推动VEI 系统最优均衡的实现；提高估价只会使W1的进化稳定策略偏向于不利于VEI 的高价竞标。

对照图3（1），仍然取值y0为0.2，I 为120 万股，h 为8.5 元/股，l 为7 元/股，V1保持不变，还是6 元/股，只改变V2，增加为6.97 元/股，其余参数保持不变动，得到图4（2）的竞标行为演化情形。因本算例符合0.49I1＜I≤0.49Is，伴随企业2 作出更高估价，该企业会青睐于选择高股价参与竞标策略；而W1则偏向于主动出击的低价竞标，尽可能先中标，赢得注资优先权，最大限度引进投资，促使创投企业先购入W1的49%股权，充分利用投资提升自身技术水平及创新能力。此种情境下，C（0，1）是ESS，竞标活动趋向于被优化的可能性渐增，VEI 市场向着有利于创投企业的方向发展。

总之，为了追求最优均衡，科技型中小企业应强化面向VEI 的企业价值评估体系，可引入第三方权威估价机构，科学衡量公司价值，结合自身实力和VEI 投资强度确定合理的股权估价。引资能力弱的科技型中小企业应始终持有较高估价，主要是出于量力而行以及规避低价竞争的考虑；而引资能力强的科技型中小企业应放低估价以提高预期收益，有利于低价竞标出让股权。两类企业要确保股权估价的动态性、灵活性、系统性及可信度。同时，政府适度介入，提高VEI 竞标的公信力和透明度，为创投企业提供公平公正公开的投资环境。

图4 博弈方股权估价对VEI 分享演化稳定过程的影响

综上，仿真研究印证了本文构建的VEI 竞标的演化博弈的复制动态特性及ESS 的存在性，也支持3.4 提出的ESS 的影响参数、影响机理及规避不理想均衡的参数选择。

五、结语

本文基于演化博弈论研究VEI 竞标策略的演化稳定性、影响因素及相关机理。考虑创投企业与科技型中小企业的投融资数量差异，分别探讨三类情形下科技型中小企业博弈的竞价比例演化路径、趋势及均衡解稳定性，得出普适性规律，并给出算例验证，最后提出实现科技型中小企业竞标博弈的最优演化稳定均衡的对策建议。有价值的结论有：ESS 受到博弈方竞价选择起始比例、投融资数量差异、博弈方得益的多重影响。Pareto最优均衡态是指博弈方以低股价出让股权给创投企业，提升投资效率，谋求VEI 综合效应最大化。为实现博弈方低价竞标，可以调整以下影响因素，并设置如下竞标规则引导局中人向最优ESS 变化：

（1）在股权换投资博弈的起始阶段，博弈方的低价策略选择比例越大，竞标过程向最优ESS点A（0，0）发展的可能性越大，收敛速度越快，创投企业作为招标方有必要严把入门关，实施正面引导、发布声明等信息传递方式及激励博弈方的举措，尽可能提高低竞价博弈方的初始比例，有意识地优化博弈方种群结构，力排选择高竞价策略的科技型中小企业进入，力挺选择低竞价策略的科技型中小企业参与竞标。

（2）政府引资部门也应配合创投企业做好竞标监管，倡导及鼓励低价竞标，杜绝高价暴利，营造外部技术创新的理想外部环境，也能提升自主或二次创新能力，助推技术进步。

（3）适当减少VEI 的单次投资量，改变大量少次投资为少量多次投资，每次投资数以不超过博弈方的股权出让数较低者为宜，更利于实现VEI 投资市场最优均衡。

（4）鉴于最优均衡在VEI 数小于中小企业出让数较小者的条件下最易于实现，竞标前务必保密VEI 数更能刺激科技型中小企业让利，加强竞标方的引资竞争性。

（5）设置低于科技型中小企业所报高股价的竞价上限，同时提高科技型中小企业报出的低股价，即缩小竞标企业报价区间，能使科技型中小企业交互策略演化路径渐趋于最优均衡态，同时以低价出让股权而引入投资。

（6）博弈方应结合自身实力和VEI 规模确定合理的股权估价，引资能力弱的企业应始终持有更高估价，而引资能力强者应降低估价，如此才能有利于较强科技型中小企业低价出让股权，实现竞标结果最优，更有利于提高VEI 的综合效应及各方福利。

然而，本文的理论假设及模型分析存在以下局限性：演化分析是基于包含大量科技型中小企业的种群而展开，对于仅有少数寡头的自然垄断产业的VEI 活动，上述结论显然是不合适的；再者，资本市场的系统性风险、难预知性、强波动性及可操纵性是影响被投资企业股权竞价的现实因素，该演化博弈分析框架在此方面存在缺失和遗憾，也是无能为力去解决的；实际上，科技型中小企业竞标成本极大地影响着支付水平，该模型也未考虑，如果竞标费用很高，以上结论势必要修正；本文中三类支付矩阵只是依据投资数量而划分，但没有探讨较为现实的局中人可信威胁、信息传递机制等信息经济学的新问题或典型问题，因此适用范围较为有限；最后还有一点，科技型中小企业虽然面对VEI 不断学习改进，进行反复的竞标博弈，但是没有对竞标过程再细分为常见的项目竞标中的技术标、价格标及服务标等多阶段，而分步骤、分标的地研究博弈方的ESS，这也是未来研究有待突破的重点。