西藏高原林芝云杉树高与胸径异速生长方程建模

普布顿珠，边巴多吉，郭其强，朱雪林，朱 莉

(1.西藏自治区林业调查规划研究院，拉萨 850000； 2.西藏高原生态研究所，西藏 林芝 860000； 3.西藏林芝高山森林生态系统国家野外科学观测研究站，西藏 林芝 860000； 4.西藏拉萨师范高等专科学校，拉萨 850007)

西藏高原林芝云杉树高与胸径异速生长方程建模

普布顿珠1，边巴多吉1，郭其强2,3，朱雪林1，朱 莉4

(1.西藏自治区林业调查规划研究院，拉萨 850000； 2.西藏高原生态研究所，西藏 林芝 860000； 3.西藏林芝高山森林生态系统国家野外科学观测研究站，西藏 林芝 860000； 4.西藏拉萨师范高等专科学校，拉萨 850007)

以150株西藏高原林芝云杉解析木资料为样本，利用Excel 2003软件中的5种数学模型对林芝云杉的树高与胸径异速生长的进行建模，并分析其精度；结果显示幂指数方程H=1.68D0.777拟合效果最佳(R2=0.981)；该模型可用于西藏高原东南部快速准确地测算林芝云杉平均树高，也可为计算立木材积、编制出材率表和评价林分的立地质量提供基础数据，对于了解林芝云杉生长状况和指导当地林业生产具有重要作用。

林芝云杉；树高；胸径；异速生长方程

植物的异速生长主要是研究植物个体大小和其他属性之间的非线性关系，通常以幂指数(Y=axb)形式表示。在森林资源调查中树木的胸径、树高是最重要的两项因子，二者的相互关系称为树高曲线，也属于植物异速生长关系的一种[1]。通过应用异速生长方程研究树高与胸径关系，一方面可以求算林分各径阶相对应的平均树高，尤其是林分平均胸径相对应的林分平均高；另一方面可用于计算树干材积、编制出材率表、评价立地质量等[2-3]，对于指导当地林业生产具有重要的现实意义。

林芝云杉[4](Picealikiangensisvar.linzhiensis)为松科云杉属常绿高大乔木，为西藏亚高山暗针叶林的主要建群种之一，主要生长在藏东南的林芝地区和昌都地区。林芝云杉不仅是青藏高原特有的速生用材树种，而且在提供工业用材、维护生态环境和构建高原生态屏障等方面发挥着重要的作用。学者们针对林芝云杉开展了群落特征与林分生产力[4-5]、生态[6]水文功能和光合特性[7]等方面的研究，而对该树种在高寒生境的生长过程及状况了解甚少。鉴于此，本研究拟利用西藏林芝云杉解析木数据拟合胸径与树高关系的异速生长方程，以便为当地的林业生产提供基础资料。

1 材料与方法

1.1 研究地概况

研究区包括西藏东南部的林芝地区和昌都地区，位于雅鲁藏布江中游河谷地带。属高原温带半湿润季风气候，年平均气温6.5℃，最冷月(1月)平均气温0.3℃，最热月(7—8月份)平均气温15.6℃，无霜期170d，年降水量600～900mm，4—10月份降水量占全年降水量的85%左右；土壤类型主要为山地棕壤和暗棕壤；亚高山针叶林区，地带性植被以高山松林(Pinusdensata)、高山栎林(Quercussemecarpifolia)、林芝云杉和急尖长苞冷杉林(Abiesgeorgeivar.smithii)为主。

1.2 试验材料

为满足建模精度要求，林芝云杉样本按18个径阶段(分别为2，4，6，8，10，12，14，16，18，20，22，24，26，32，38，40，44和50cm)，且每个径阶组内的样本按个体高度均匀分布，并考虑地形、坡位、年龄和个体生长状况等因子，共选取具有代表性的个体共150株。在离地面1.3m处用围尺测量胸径，再用超声波测高测距仪(Vertex IV，瑞典产)测定树高。

1.3 数据处理

将林芝云杉样本按2 cm的径阶分组并统计株数，计算各径阶的平均胸径和树高，详见表1。

采用Excel 2003软件进行数据建模和统计分析，用Office 2003绘制图形。

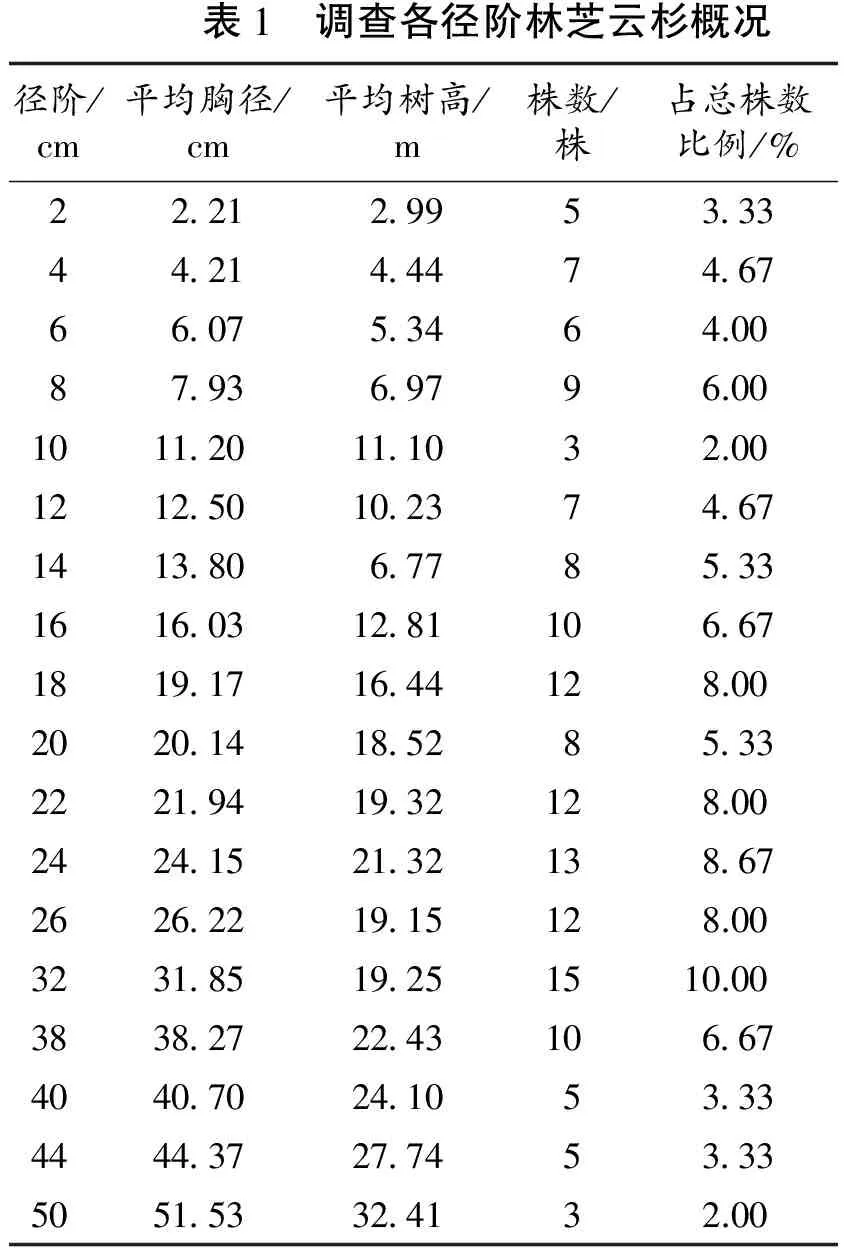
表1 调查各径阶林芝云杉概况径阶/cm平均胸径/cm平均树高/m株数/株占总株数比例/%22 212 9953 3344 214 4474 6766 075 3464．0087 936 9796．001011 2011 1032．001212 5010 2374 671413 806 7785 331616 0312 81106 671819 1716 44128．002020 1418 5285 332221 9419 32128．002424 1521 32138 672626 2219 15128．003231 8519 251510．003838 2722 43106 674040 7024 1053 334444 3727 7453 335051 5332 4132．00

2 结果与分析

2.1 径阶分析

林芝云杉按胸径<10，10～19，20～39，≥40cm的株数分别统计(结果见图1)，胸径<10cm的占20%，10～19cm的占30%，20～39cm的占41.33%，≥40cm的占8.67%。根据前人对西藏林芝云杉林生长状况的研究[5,8-9]结果表明，该树种胸径在20～39cm的个体处于迅速生长期。说明本研究中的样木选择基本以中龄期和成熟期的个体为主，同时兼顾幼龄期和老龄期个体。

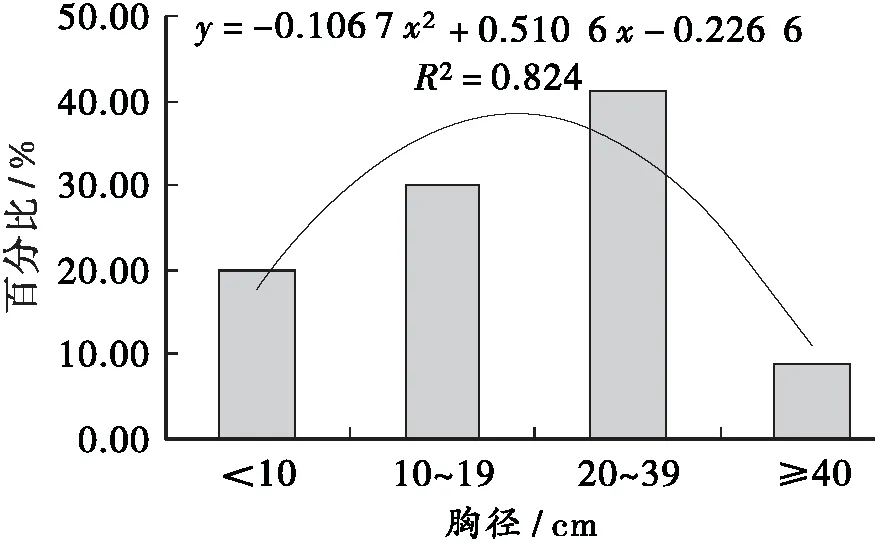
图1 林芝云杉胸径分布比例

2.2 建模与检验

2.2.1 建模

根据表1中各径阶实测的树高平均值，以胸径为横坐标，树高平均值为纵坐标，绘制径阶与树高分布的散点图(图2)。通过观察散点形状与分布趋势，初步选定可能符合散点分布趋势的几种相关模型，见表2。根据表1的平均胸径与对应平均树高成对数据，利用Excel2003软件拟合所选几种相关模型，得各模型参数及复相关系数R2。表2中：H是平均树高的回归估计值；D是各径阶的平均胸径；a，b，c为参数。

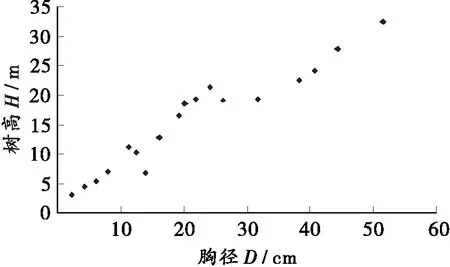
图2 林芝云杉树高与胸径散点图

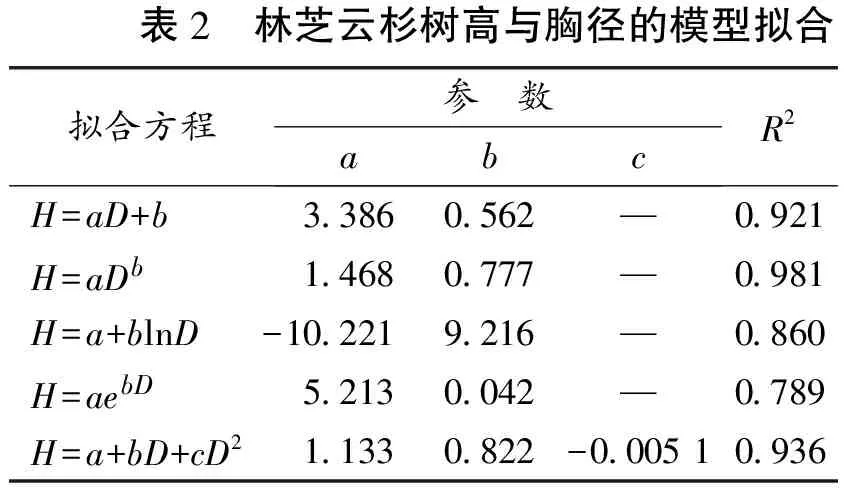
表2 林芝云杉树高与胸径的模型拟合拟合方程参 数abcR2H=aD+b3 3860 562—0 921H=aDb1 4680 777—0 981H=a+blnD-10 2219 216—0 860H=aebD5 2130 042—0 789H=a+bD+cD21 1330 822-0 00510 936

模型H=a+blnD和H=aebD拟合方程的相关系数R2较小；H=aD+b，H=aDb和H=a+bD+cD2复相关指数R2均大于0.92，说明其拟合效果相对较好。5个模型中方程H=aDb的相关系数最高，为0.981，说明其拟合效果最好。

2.2.2 显著性检验

对上述胸径与树高的回归方程H=aDb进行方差分析，见表3，F=313.207>F0.01(1，149)=6.83，说明方程H=aDb能极显著地描述林芝云杉生长过程中树高与胸径的关系。表3回归分析中平均树高的差异，一方面来自于因个体对应的胸径不同引起；另一方面是由其它随机因素引起，因此回归方差和残差的比值较大，表明回归方程愈显著[10-11]。

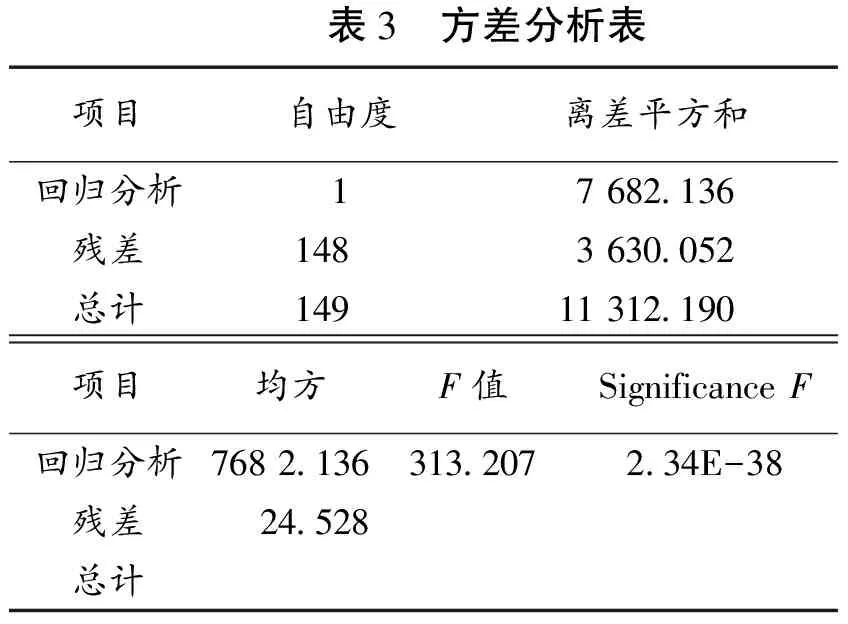
表3 方差分析表项目自由度离差平方和回归分析17682 136残差1483630 052总计14911312 190项目均方F值SignificanceF回归分析7682 136313 2072 34E-38残差24 528总计

3 结论

林芝云杉的横向和纵向生长过程与其他乔木一样，要经历慢、快、慢的过程，幂指数的变化趋势能够反映这一变化规律。在排除环境发生剧烈变化的前提条件下，植物的生长量是可预见的[12]，应用幂指数生长方程完全可以对此做出预测[13]。

本研究通过对西藏高原林芝云杉不同径阶个体树高与胸径的测定，应用数学模型拟合树高与胸径的异速生长方程。结果表明：林芝云杉的树高与胸径关系的最佳模型为H=aDb，具体方程为H=1.68D0.777，相关系数为R2=0.981。该模型可用于西藏高原东南部快速准确地测算林芝云杉平均树高，也可为计算立木材积[14]、编制出材率表[15]和评价林分的立地质量[16-18]提供基础数据，这对指导当地林业生产具有重要的现实意义。

[1] 赵敏,丁慧勇.上海水杉树高与胸径关系模式分析[J].上海师范大学学报：自然科学版,2009,38 (5)：531-535.

[2] 龙本楼,林顺根.黔东南杉木树高与胸径相关研究[J].中国新技术新产品,2011(5)：237.

[3] 肖志坚.福建柏树高—胸径一元线性模型的改进[J].宁夏农林科技,2011,52(7)：56-57.

[4] 罗建,方江平,王国严.林芝云杉群落特征的研究[J].热带亚热带植物学报,2011,19(2)：113-119.

[5] 方江平.西藏南伊沟林芝云杉林生物量与生产力研究[J].林业科学研究,2012,25(5)：582-589.

[6] 方江平,项文化,刘韶辉.西藏南伊沟原始林芝云杉林水文学过程的水化学特征[J].林业科学,2010,46(9)：14-19.

[7] 肖文发,韩景军,郭志华,等.西藏林芝云杉针叶净光合速率对环境因子的响应[J].林业科学研究,2003,16(3)：299-305.

[8] 陈克龙,刘晓宏.喜马拉雅冷杉和林芝云杉年轮稳定碳同位素气候意义比较[J].盐湖研究,2003,11 (2)：29-34.

[9] 韩景军,肖文发,郭泉水,等.西藏林芝县林芝云杉幼林更新与物种多样性指数研究[J].林业科学,2002,38(5)：166-168.

[10] 郑传英.四川桤木林分各主要生长因子间相关性研究[J].安徽农学通报：上半月刊,2010, 16(17)：161-162.

[11] 明安刚,唐继新,于浩龙,等.桂西南米老排人工林单株生物量回归模型[J].林业资源管理,2011(6)：83-87,93.

[12] 张彩琴,杨持.植物生长模拟与数学模型研究[J].内蒙古大学学报：自然科学版,2006, 3(4)：435-440.

[13] 谭美,王四清.观赏植物生长模拟模型研究进展[J].园艺学报,2010,37(9)：1523-1530.

[14] 马友平,沈作奎,艾训儒,等.材积与胸径关系的Richards衍生模型研究[J].生物数学学报, 2010,25(1)：122-126.

[15] 吴明山,胥辉.度量误差对材积模型的影响及参数估计研究[J].北京林业大学学报,2008, 30(5)：83-86.

[16] 郭晋平,张浩宇,张芸香.森林立地质量评价的可变生长截距模型与应用[J].林业科学,2007,43(10)：8-13.

[17] 骆期邦,吴志德,蒋菊生,等.用于立地质量评价的杉木标准蓄积量收获模型[J].林业科学研究,1989,2(5)：447-453.

[18] 赵总,张兆国,谢德兵,等.立地条件对川滇桤木生长的影响[J].江苏农业科学,2011,39(6)：312-313．

Height-DiameterAllometricGrowthEquationsforPicealikiangensisvar.linzhiensisinTibetPlateau

Pubu Dunzhu1，Bianba Duoji1，GUO Qiqiang2,3，ZHU Xuelin1，ZHU Li4

(1.Forest Inventory and Planning Institute of Tibet Autonomous Region, Lhasa 850000 ,Tibet, China； 2.Research Institute of Tibet Plateau Ecology，Linzhi 860000, Tibet, China； 3.National Forest Ecosystem Research Station in the Sejila Mountain of Tibet，Linzhi 860000, Tibet, China；4.Teachers College in Lhasa，Lhasa 850007 ,Tibet, China)

In this paper, five height-diameter allometric growth equations were evaluated by making use of Excel 2003 software, based on the data of 150 parse trees ofPicealikiangensisvar.linzhiensisin Tibet plateau, and every equation’s accuracy was analyzed, the results showed that: The exponential equation (H=1.68D0.777) was the best fit (R2=0.981), it can be used to calculate the average tree height ofPicealikiangensisvar.linzhiensisin southeastern Tibet plateau precisely and rapidly , and can provide the basic data for the calculation of tree volume, compilation of merchant volume table and the evaluation of forest-site quality, which is very important for understanding the growing status ofPicealikiangensisvar.linzhiensisand guiding forestry production.

Picealikiangensisvar.linzhiensis;tree height;diameter at breast height(DBH);allometric growth

2013—11—26

普布顿珠(1973—)，男，西藏昌都类乌齐人，工程师，从事森林资源保护与培育的相关研究。

边巴多吉，副研究员。

S 758

A

1003—6075(2014)01—0013—03