激光模式对典型金属材料烧蚀影响的数值模拟研究

孙震宇，冉宪文，汤文辉，徐志宏

（国防科学技术大学 理学院 工程物理研究所，长沙 410073）

0 引言

激光照射引起的材料熔化、气化、焦化、喷射或燃烧使得材料表面发生质量迁移的现象称为激光烧蚀。激光烧蚀是激光加工、激光毁伤破坏的基本物理过程，因而也是此领域的研究热点[1-4]。国外的研究较早，Mezines 等[5]考虑了重复频率激光对薄板的加热问题；Warren 等[6]主要考虑了一维烧蚀问题，包括材料的激光吸收系数与温度相关性以及发生气化或熔化的情形。El-Niclany 等[7]对均匀、连续激光辐照下半无限体材料的加热、熔化和气化问题进行了解析研究。国内也开展了大量研究，赵伊君[8]研究了激光与金属相互作用时，烧蚀蒸气的运动可用辐射流体力学方程描述；汤文辉等[9]采用了光滑粒子流体动力学（SPH）方法对典型靶的激 光烧蚀进行了数值模拟，研究了单层铝靶和环氧树脂/铝双层靶在激光辐照下的烧蚀形貌与温度场；常浩等[10]建立了一个复杂的一维热传导和流体动力学模型，并计算研究了激光功率密度对纳秒激光烧蚀冲量耦合影响。

从相关研究结果来看，影响激光对材料烧蚀效果的主要因素是激光功率密度和材料的光吸收系数，而光吸收系数又与材料表面温度相关——温度越高光吸收系数越大（对本问题研究的材料而言）。提高激光功率密度则可以增强对材料的烧蚀效果，然而对于平均功率一定的重频激光器，占空比减小可以增加激光峰值功率，使得材料有更多的时间将自身的热量通过热对流耗散到周围空气中，从而降低材料表面温度，使得光吸收系数减小。

本文利用自编的激光烧蚀模拟程序LAMP，开展重频激光对典型金属材料的烧蚀过程数值模拟研究，并考察占空比、平均功率密度、重频频率等对烧蚀时间的影响。

1 理论模型

1.1 热传导方程

激光烧蚀的热传导方程[11]为

式中：ρ为材料密度；为比内焓；→为热流密度。

固体的热传导遵循傅里叶导热定律，即：

式中k为导热系数，也叫热导率。综合上述两式可以给出各向同性材料的热传导方程为

1.2 边界条件

在烧蚀条件下，计算模型将涉及两类边界条件，即固定边界条件和移动边界条件[12]。固定边界条件可分为Dirichlet 边界、Neumann 边界和Robin边界3 类；移动边界条件可分为烧蚀边界条件和相边界条件。本文主要考虑等温边界及热流边界。

1.3 金属材料的反射系数的计算

根据电动力学所描述的电磁波与分层介质的运动方程以及Drude 公式，金属材料的反射系数可以表示为

式中：c为真空中的光速；λ为入射激光波长；0σ为材料的直流电导率。对于金属来说，其电导率随温度变化的关系为

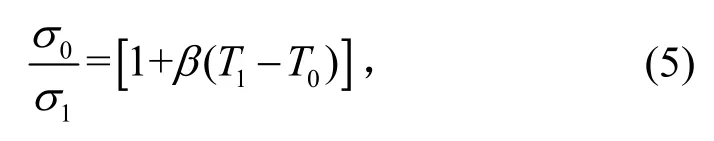
其中β为温度系数，取决于材料的性质。图1给出了铝、镁和钛3 种金属材料对1.064 µm 波长入射光的反射率随温度变化的关系。

图1 铝、镁和钛反射率随温度的变化关系Fig.1 Variation of aluminum, magnesium and titanium’s reflectance with temperature

1.4 SPH 方法

本文采用光滑粒子流体动力学法[13]（Soothed Particle Hydrodynamics，SPH）来编制，其优势是使得处理材料烧蚀相对简单，只需删除相关SPH粒子即可。SPH 法的基本思想是，根据某时刻各粒子的参量，通过核函数插值计算得到下一时刻各粒子的参量，其关键是插值计算。

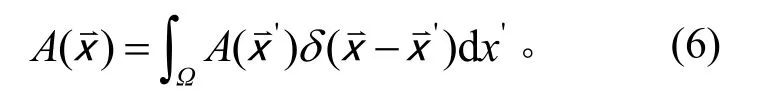
在柱坐标下，相应的热传导方程为

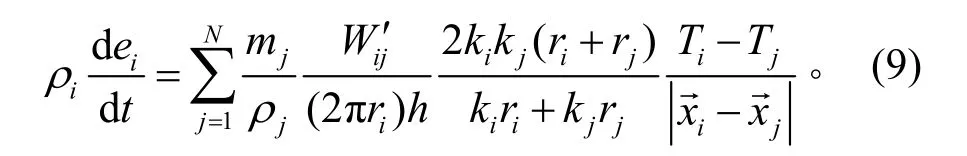
2 计算结果和分析

金属吸收激光的能量，导致辐照面的温度升高；当激光能量密度足够大时，则会引起金属的熔化、气化，发生烧蚀现象。图2给出了计算所用金属材料的尺寸，激光波长取为1.064 µm，圆形光斑半径为0.564 cm，激光在金属表面的反射系数采用Drude公式进行计算。计算中主要考虑了连续、重频和占空比的影响，总计算时间为1 min。

图2 激光辐照金属板计算模型Fig.2 Calculation model of metal plate irradiated by laser

2.1 激光对铝的烧蚀效应

对于重复频率激光，我们分别考虑平均功率5000 、6000 W，占空比0.045、0.2 和0.4 条件下Nd∶YAG 激光对铝靶板的烧蚀影响。

对于占空比为0.045、平均功率为5000 W 的Nd∶YAG 激光，共计算25、50、75、100、200、300、400、500 Hz 八种重复频率的工况，总计算时间为1 min。图3给出了25、500 Hz 两种重复频率情况下发生烧蚀并贯穿铝靶板时的温度场，若没有贯穿则其温度场为辐照1 min 后的情况。

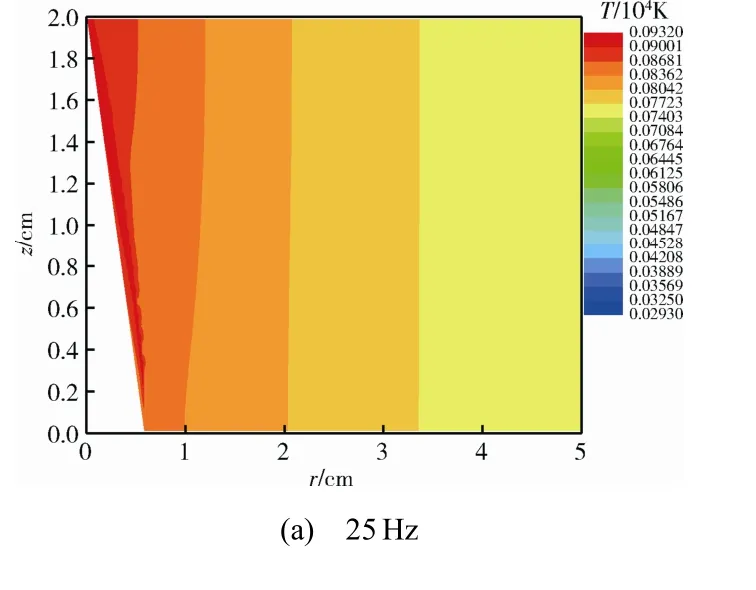
图3 平均功率5000 W、占空比0.045 的重频激光烧蚀 贯穿铝靶板时的温度场Fig.3 Temperature field of ablation through the aluminum plate by repeated frequency laser of 5000 W in average with duty ratio of 0.045

2.2 激光对镁的烧蚀效应

分别考虑平均功率2500、3000 W，占空比0.045、0.2 和0.4 条件下的Nd∶YAG 激光对镁靶板的烧蚀影响。对于占空比为0.045，平均功率为 2500 W 的Nd∶YAG 激光，同样进行烧蚀计算模拟。图4给出了25、500 Hz 两种重复频率情况下发生烧蚀并贯穿靶板时的温度场，若没有贯穿则其温度场为辐照1 min 后的情况。

图4 平均功率2500 W、占空比0.045 的重频激光烧蚀 贯穿镁靶板时的温度场Fig.4 Temperature field of ablation through the magnesium plate by repeated frequency laser of 2500 W in average with duty ratio of 0.045

2.3 激光对钛的烧蚀效应

分别考虑平均功率1500、2000 W，占空比0.045、0.2 和0.4 条件下的Nd∶YAG 激光对钛靶板的烧蚀影响。对于占空比为0.045、平均功率为1500 W的Nd∶YAG 激光，进行烧蚀计算模拟。图5给出了25、500 Hz 两种情况下发生烧蚀并贯穿靶板时的温度场，若没有贯穿则其温度场为辐照1 min后的情况。

图5 平均功率1500 W、占空比0.045 的重频激光烧蚀 钛靶板时的温度场Fig.5 Temperature field of ablation on the titanium plate by repeated frequency laser of 1500 W in average with duty ratio of 0.045

3 计算结果分析

3.1 不同频率对烧蚀时间的影响

分析模拟计算的结果，在平均功率5000 W、占空比为0.045 的激光辐照下，25、50、75、100、200、300、400、500 Hz 激光均烧蚀贯穿了2 cm 厚的铝靶板，烧蚀贯穿的时间分别为44.60、47.14、48.31、48.85、49.85、50.26、50.36、50.34 s，这说明25 Hz 激光贯穿所需的能量最少。

图6给出了对占空比为0.045 的激光辐照下，平均功率和频率不同的激光对钛的烧蚀时间。

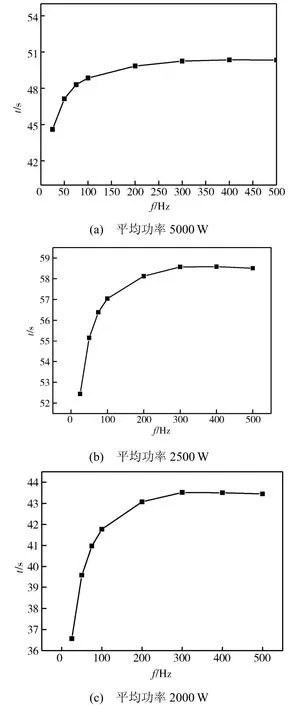
图6 占空比0.045，不同平均功率辐照下重频激光对 钛靶板的烧蚀时间Fig.6 Ablation time of titanium irradiated by repeated frequency laser of various average powers with duty ratio of 0.045

从图6可以看出，在平均功率一定的条件下，重复频率较小的激光烧蚀贯穿2 cm 厚的钛所需时间较少；但当频率大于200 Hz 时，频率对激光烧蚀的影响差别不大。

3.2 不同占空比和功率对烧蚀时间的影响

对于铝，不同占空比对烧蚀贯穿时间的影响如图7所示：占空比越小，烧蚀贯穿的时间越短，并且频率越低，相互间的时间差异越大。总的来看，占空比0.045、频率25 Hz 的重频激光烧蚀时间最短。由图7可以得到，在光斑大小不变的条件下，激光功率越大，则激光烧蚀所需的时间越短。

图7 不同占空比对激光烧蚀贯穿铝的时间对比Fig.7 Comparison of aluminum ablation time by the repeated frequency laser with various duty ratios

对于镁，不同占空比对烧蚀贯穿时间的影响如图8所示。曲线变化态势和分析结论同铝的情况。

图8 不同占空比对激光烧蚀贯穿镁的时间对比Fig.8 Comparison of magnesium ablation time by the repeated frequency laser with various duty ratios

对于钛，在平均功率1500 W 的激光辐照下，只有25 Hz 的烧蚀贯穿了2 cm 厚的钛，其他条件下均未能烧蚀贯穿。当平均功率达到2000 W 时，在不到1 min 的时间里就可以烧蚀贯穿2 cm 厚的钛，如图9所示。随着激光功率的增加，烧蚀所需的时间缩短。

图9 在平均功率2000 W 下不同占空比对激光烧蚀钛 的时间对比Fig.9 Comparison of ablation time of titanium by the repeated frequency laser with various duty ratios and of 2000 W in average

4 结论

本文采用SPH 方法编制了用于计算激光烧蚀材料效应的二维计算程序，模拟计算并分析了在不同激光频率、占空比及平均功率作用下金属靶的温度场，得到结论如下：

1）对于同样材料的金属靶，当激光光斑和平均功率相同时，重复频率较低的烧蚀贯穿金属靶所需时间较少，且占空比越小则烧蚀贯穿时间越短。

2）对于同样的金属靶，在光斑大小不变的条件下，随着激光平均功率的增加，烧蚀贯穿时间缩短。

（References）

[1]任天宇, 王洋, 薛阳, 等.长脉冲激光与金属相互作用影响分析[J].光电技术应用, 2011, 26(6)∶28-32 Ren Tianyu, Wang Yang, Xue Yang, et al.Analysis of long pulse laser-metal interaction[J].Electro-Optic Technology Application, 2011, 26(6)∶28-32

[2]傅广生, 王世俊, 丁学成, 等.激光参量对脉冲激光烧蚀粒子初始参数的影响[J].人工晶体学报, 2010, 39(6)∶239-243 Fu Guangsheng, Wang Shijun, Ding Xuecheng, et al.Influence of laser parameters on initial parameters of the ablated partcles produced by pulsed laser ablation[J].Journal of Synthetic Crystals, 2010, 39(6)∶239-243

[3]胡湛, 齐莹, 杨鼎, 等.整形飞秒激光金属材料精细加工[J].强激光与粒子束, 2012, 24(10)∶2381-2385 Hu Zhan, Qi Ying, Yang Ding, et al.Metal micromachining with shaped femtosecond laser pulses[J].High Power Laser and Particle Beams, 2012, 24(10)∶2381-2385

[4]Tong Yonggang, Bai Shuxin, Zhang Hong.Laser ablation behavior and mechanism of C/SiC composite[J].Ceramics International, 2013, 39(6)∶6813-6820

[5]Mezines S A, Fivel H J.Thermal performance of materials exposed to pulsed laser heating, AIAA Paper 1981-1149[R]

[6]Warren R E, Sparks M.Laser heating of a slab having temperature-dependent surface absorptance[J].Journal of Applied Physics, 1979, 50∶7952-7957

[7]El-Niclany M M, El-Adani M K, Kutub A A, et al.Analytic approach for melting and evaporation of a solid by a pulsed laser[J].Acta Phys Hugarica, 1986, 59∶291-296

[8]赵伊君.激光与金属相互作用时涉及的原子分子物理问题[J].物理学进展, 1989, 9(4)∶429-450

[9]汤文辉, 冉宪文, 徐志宏, 等.强激光对靶材烧蚀效应的数值模拟研究[J].航天器环境工程, 2010, 27(1)∶32-34 Tang Wenhui, Ran Xianwen, Xu Zhihong, et al.Numerical simulation of high intensity laser ablation of materials[J].Spacecraft Environment Engineering, 2010, 27(1)∶32-34

[10]常浩, 金星, 叶继飞, 等.激光功率密度对纳秒激光烧蚀冲量耦合影响的数值模拟[J].推进技术, 2013, 34(10)∶1426-1431 Chang Hao, Jin Xing, Ye Jifei, et al.Numerical simulation of laser power density effect on nanosecond laser ablation impulse coupling[J].Journal of Propulsion Technology.2013, 34(10)∶1426-1431

[11]谷超豪, 李大潜, 陈恕行, 等.数学物理方法[M].上海∶上海科学技术出版社, 1978∶31-46

[12]Dowden J M.The mathematics of thermal modeling∶an introduction to the theory of laser material processing[M].New York∶Chapman &Hall/CRC, 2001∶56-70

[13]Chen J K, Beraun J E, Carney T C.Corrective smoothed particle method for boundary value problems in heat conduction[J].Int J Num Math Engineering, 1999, 46∶231-252