推力器真空羽流热效应计算模型修正及 误差分析
王黎珍,史纪鑫,郑世贵
(北京空间飞行器总体设计部,北京 100094)
0 引言
在航天器进行变轨及姿态控制调整时,推力器工作可能产生羽流扰动力/力矩、羽流热和污染效应。随着航天器安装的推力器种类和数量越来越多,与羽流相关的各种问题日趋凸显,已引起了设计部门高度重视,开展了羽流效应尤其是热效应的大量研究。对羽流热效应的数值计算至关重要:若分析过于保守将会导致热防护过设计;若估计不足则可能导致星上设备过热。因此,深入开展推力器真空羽流热效应精确评估是合理进行热控设计的前提和条件。
推力器真空羽流热效应的计算分两大步骤:羽流流场的计算和羽流对航天器表面冲击作用的计算分析。推力器真空羽流流动状态极为复杂,可分为连续流(羽流核心区)、过渡流和自由分子流(羽流外围区)等3 种流动状态[1]。对于连续流区域,通常用CFD 方法数值求解N-S 方程以得到流场[2-3]。对于过渡流和自由分子流区域,采用半经验的工程模型(点源模型)[4-5]或基于DSMC 算法[6-8]的数值仿真分析得到流场。目前,无论是采用CFD/DSMC的数值求解方法,还是采用半经验的工程模型求解方法,羽流内外流场的求解精度均在工程可接受的范围内。
在羽流对航天器表面冲击作用的计算分析中,羽流冲击航天器表面的特性模型的选择是影响羽流热效应计算结果的关键因素。模型给出气体分子在固壁上的运动方式,反映气体分子与固壁间相互作用时力和热的传递过程。根据气体与固壁间相互作用方式的不同,模型分为Knudsen模型、Nocilla 模型和Lord 模型[9]。Knudsen 模型是对经典的Maxwell 模型的改进,认为羽流分子撞击航天器表面时存在吸附、漫反射和镜面反射3种运动方式,并用相应的系数表征各运动方式的占比。Nocilla 模型和Lord 模型则以Knudsen 模型为基础,对羽流分子反射方向和范围做出一定的限制和假定。工程中一般推荐采用Knudsen 模型计算羽流热流效应。
本文首先对推力器羽流内外流场进行计算;然后对Knudsen 模型中的关键参数进行讨论,明确这些参数对羽流热效应计算的敏感度,并用理论经验公式对关键参数的取值范围进行初步估算;最后利用MBB 公司10 N 推力器羽流热流试验数据,采用遍历搜索的方法对Knudsen 模型中关键参数的取值进行精确评估,使得羽流热流密度计算值与实验值间的偏差减小到7%左右。整个修正计算大幅度地提高了羽流热效应计算的精度和可信度,验证了所采用的热流计算模型的正确性和工程可用性。
1 推力器羽流流场计算方法
本文根据燃烧室内的总温、总压等燃烧条件,气体热物理性质及喷嘴的形状计算推力器羽流核心区的气体流场。对于推力器内部的流场,考虑黏性的作用,采用有限体积方法求解N-S 方程得到。对于推力器外部喷嘴附近区域(100 倍喉部半径内)的流场,可以忽略黏性作用,采用数值求解Euler方程的方法得到。喷嘴边缘处的流场可以由在喷嘴壁面处的普朗特-迈耶(Prandtl-Mayer)方程展开得到。
本文采用点源模型法对羽流的外流场进行模拟。点源模型法的特点是简单、易理解、计算量少且又能够满足一定的工程精度要求。点源模型认为在喷管外流场中,由于气流具有高马赫数与低温特性,即使气体分子之间发生碰撞,但它们的相对速度很低,在垂直于羽流轴线方向上由于分子碰撞引起的热散射很小,可以采用点源模型来描述。具体做法是在流场中定义一个冻结面,并在其上布置一定数目的自由分子点源,而流场中任意一点的流动参数可以视为所有自由分子点源产生的流场在该点的叠加。自由分子点源产生的流场密度ρ遵循辐射衰减律,即
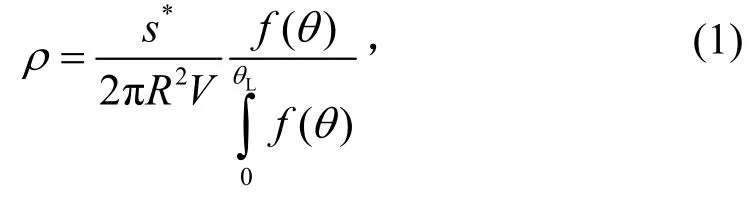
式中:V为羽流扩展极限速度;s*为喷管喉部流率;R为距喷口出口处的距离;θ为偏离羽流轴线角度;θL为P-M 扩展角;f(θ)为偏离羽流轴线角度的函数。
由于流动的基本参量不同,f(θ)在羽流核心区和边界层膨胀区的表达式不同。f(θ)在羽流核心区的表达式为
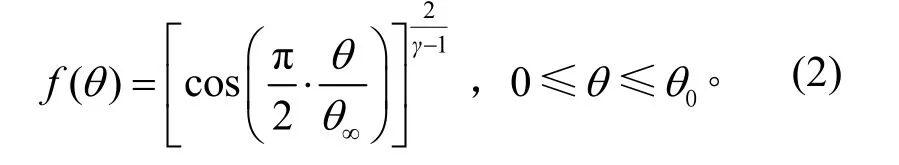
其中:γ为气体的比热比;θ∞是喷管流动极限偏转角;θ0是羽流核心区流动极限偏转角。在边界层膨胀区,引入系数β,并认为f(θ)在该区是以指数形式衰减,其表达式为
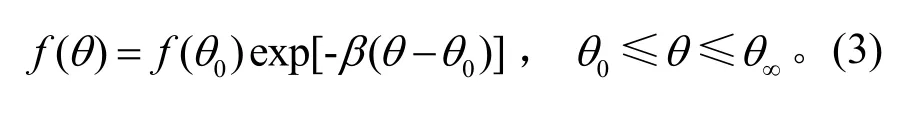
流场中的其他物理量,如压力P、温度T和极限速度V可根据一维等熵关系求出。用点源模型计算得到羽流外流场的流程见图1。
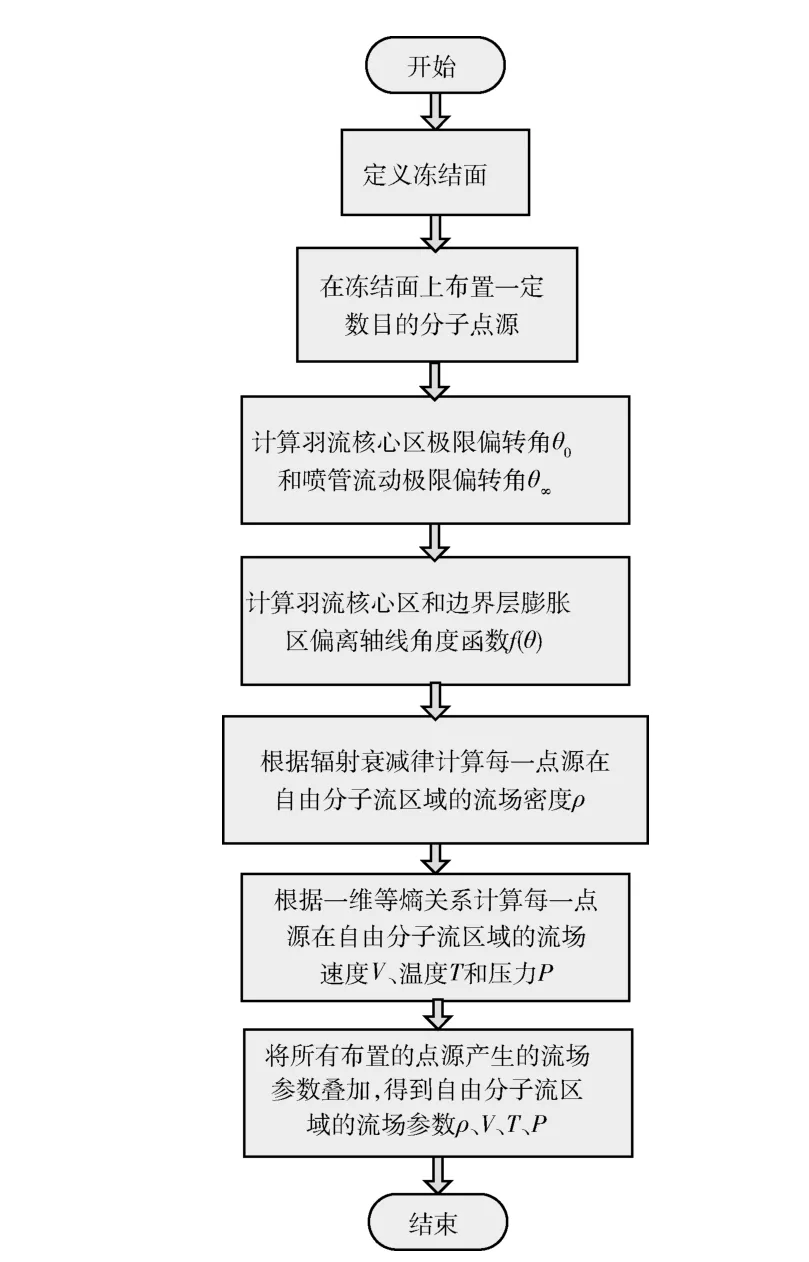
图1 点源法计算流程Fig.1 The flow chart of source flow method
2 推力器羽流热效应表面特性模型
羽流流场确定后,羽流冲击模型的选择就成为关键因素。本文首先对Knudsen 模型的特点及其关键参数对羽流热流密度的敏感度进行分析,然后通过理论经验公式对Knudsen 模型中关键参数的取值范围进行分析和估算。
2.1 Knudsen 模型分析
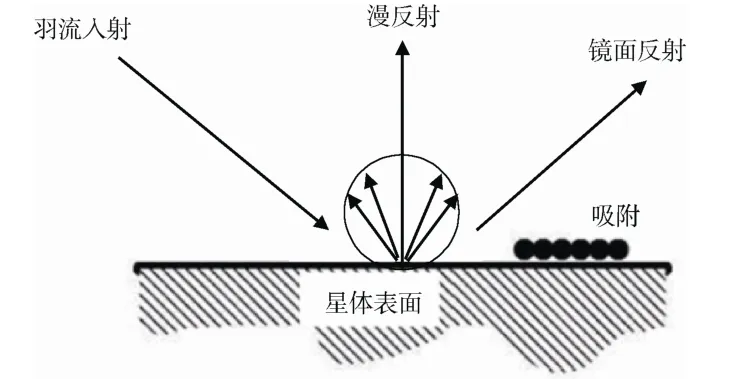
图2 Knudsen 模型中气体和表面的相互作用Fig.2 The interaction between gas and surface for the Knudsen model
羽流冲击到星体表面后会发生与固壁的相互作用及能量交换。Knudsen 模型认为羽流分子冲击到卫星表面会产生被卫星表面吸附、镜面反射和漫反射3 种运动方式(见图2),它们的发生占比分别由吸附系数λ、镜面反射系数τ和漫反射系数α确定。 漫反射系数α又称壁面热适应系数,对羽流在星体表面产生的热流密度影响很大,是真空羽流热效应数值模拟的关键参数。该参数表征了反射分子的温度在多大程度上“适应”了星体表面的温度状况。当羽流分子在固壁上发生Maxwell 反射即完全漫反射时,α=1;完全镜面反射时,α=0。Knudsen模型假设:若入射的气体分子质量为m,气体分子在与壁面作用的过程中,入射流量的λm被表面吸附,τ(1-λ)m被镜面反射,(1-τ)(1-λ)m被漫反射,即系数α、τ和λ间的关系为α=(1-τ)(1-λ)。
2.2 漫反射系数α 对羽流热流密度的敏感度分析
为了讨论漫反射系数α对羽流热效应的具体影响,本文进行了以下的数值计算假设:在距离推力器喷口100 cm 处放置接收板,假设气体与接收板表面只发生吸附和漫反射2 种作用形式。通过计算α从0(气体被星体表面完全吸附)变到1(气体被星体表面完全漫反射)时羽流热流密度的变化,得到α对羽流热效应的影响关系。计算结果如 表1所示,可以看出,羽流热流密度随α的增加而增加。气体分子被壁面完全吸附(α=0)时热流密度最小,完全漫反射(α=1)时热流密度达到最大。随着α的变化,热流密度在比较大的范围内波动,完全漫反射时的羽流热流密度值是完全吸附状态的50 倍左右。由此可见,羽流热流密度对α的变化高度敏感。
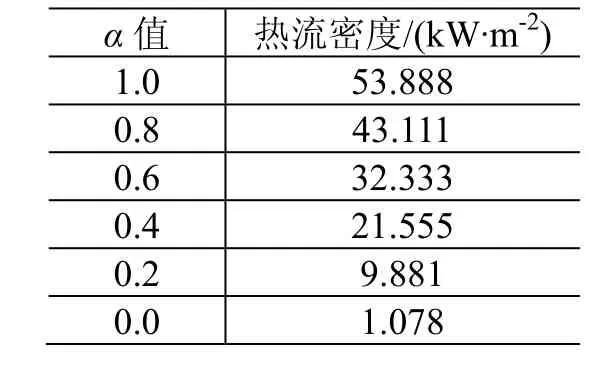
表1 漫反射系数α 变化对羽流效应的影响(τ=0)Table 1 The influence of accommodation ratio on the plume effect(τ=0)
2.3 漫反射系数α 取值范围分析讨论
通常情况下,漫反射系数的取值与燃烧产物气体分子特性、材料表面特性和材料表面温度相 关[10-11]。经过调研和资料收集,得到了H2、H2O、N2、CO2和CO 等5 种燃烧产物在表面材料为Al和Fe 时,α随表面温度T的变化如图3所示。由图可见,α的变化范围是比较宽的,对于分子量比较小的气体(H2),α的数值分布总体上<0.4,并且随温度的升高而减小;对于分子量比较大的气体(H2O、N2、CO2、CO),α的数值分布总体上>0.7。而一般情况下,羽流与航天器表面发生撞击时,存在能量交换的漫反射的发生占比最大,少量分子会发生镜面反射和吸附在航天器表面。因此,在以往航天器羽流热效应分析中,常选用完全漫反射模型进行羽流热效应计算。
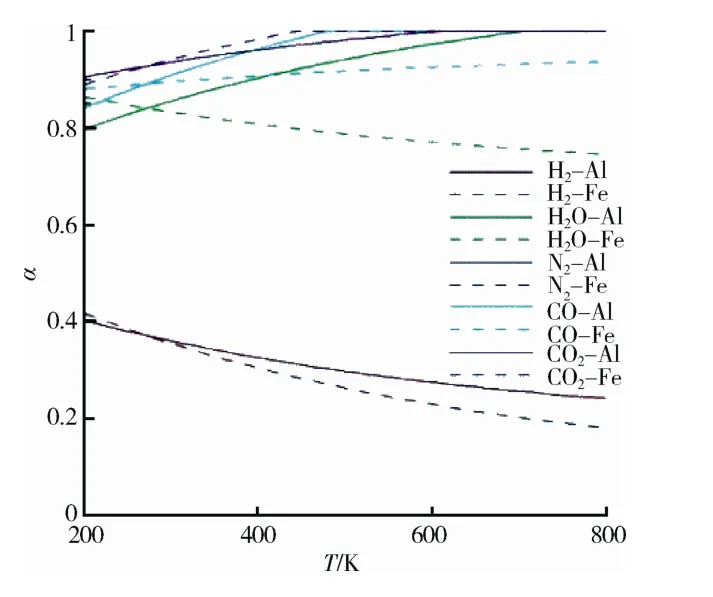
图3 常见气体在常见材料表面的漫反射系数Fig.3 The accommodation ratio of the some gases and surface
Yasar Demirel 等[12]和周志雄等[13]通过对一系列气体分子在不同温度(273~1250 K)的金属表面的漫反射系数进行分析,总结出如下关系:
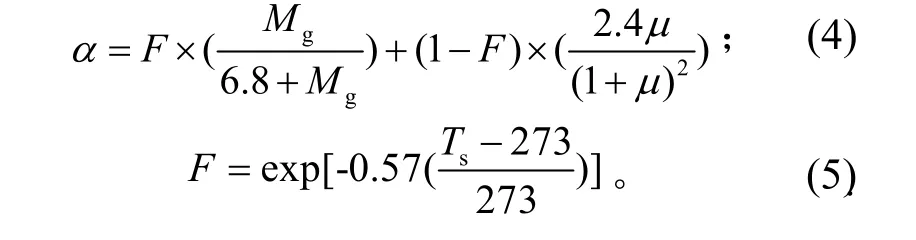
其中:µ=Mg/Ms,Mg为气体物质的分子量,Ms为固壁材料的分子量;F代表吸收层的覆盖分数,由固体表面特性和表面温度Ts决定。
对于航天器常用的单组元和双组元推力器,其燃烧产物的摩尔分数和质量分数见表2。无论对于单组元还是双组元推力器,其燃烧产物中大分子量气体(NH3、H2O、N2)均约占总质量的99%左右。表2还给出了航天器表面温度为273 K 时各燃烧产物的漫反射系数,并按照各燃烧产物的质量分数对漫反射系数进行加权平均,计算出单组元推力器和双组元推力器的综合漫反射系数分别为0.767 和0.782。
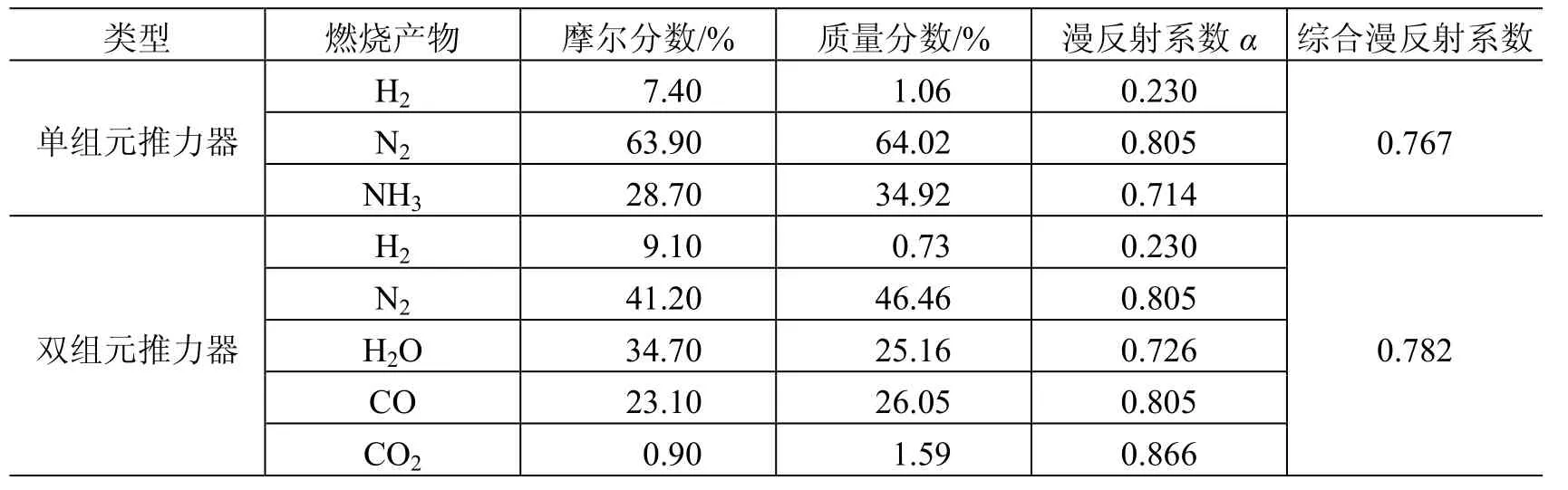
表2 推力器燃烧产物组成及漫反射系数估算Table 2 The evaluation of accommodation ratio for combustion products of thrusters
3 羽流热效应表面特性模型修正
由前述可知,羽流热流密度对漫反射系数α的变化非常敏感,而在以往的工程计算中,对α的取值比较保守(即将α取为1),这样得到的羽流热流值较大。因此在热防护设计中会出现过防护,增大质量负荷。为此,本文利用MBB 公司的 10 N推力器羽流试验数据重点开展对羽流表面特性模型的修正工作,将羽流热流密度的计算误差减小到工程允许的范围内,同时验证该模型的正确性和可信度。
3.1 MBB 10 N 推力器试验条件及结果
MBB 公司使用标称10 N 双组元推力器[14-15],在地面高真空试验舱内进行了羽流热效应测量试验。真空试验舱为直径1 m、长约2 m 的圆柱容器。推力器安装在圆柱容器中心线上,且二者的中心线重合。真空试验舱采用液氦低温系统和液氮低温系统进行冷却,最低温度可以达到20 K;真空抽气速度为0.014 m3/s,在推力器工作前舱内真空度可以达到1×10-4Pa。
羽流热效应试验重点研究了距喷口不同距离R,不同羽流角θ和不同羽流入射角β情况下的羽流热流分布,其中θ和β的定义见图4,试验结果见表3。由于受真空舱直径限制,测量时θ的最大有效值仅为40°。
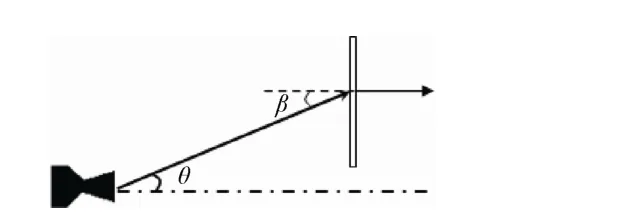
图4 推力器羽流角θ 和羽流入射角β 定义Fig.4 The definition of plume flow angle θ and the plume incidence angle β
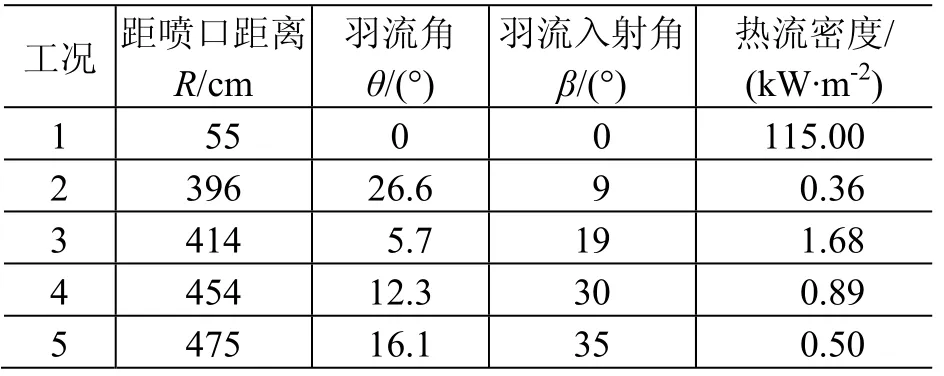
表3 MBB 10 N 推力器不同工况下羽流热试验结果Table 3 The experimental plume heating results of MBB 10 N thruster
3.2 模型修正
在羽流冲击航天器表面时,吸附现象一般发生在温度低于200 K 的敏感器等仪器表面,而对于温度较高的表面,很少发生吸附现象。因此,本文考虑的表面温度较高,计算时设吸附系数λ为0。根据推力器羽流热试验工况的设置情况,可采用Knudsen 完全漫反射模型进行分析,计算结果见 表4。可以看出,计算得到的羽流热流密度值普遍比试验值大,相对误差基本在50%以上,表明该模型夸大了羽流冲击航天器表面产生的热效应,将这些计算结果应用于工程设计显然过于保守。
为此,我们采用遍历搜索的算法,通过对Knudsen 模型中的漫反射系数α进行调整,将每次调整后的Knudsen 模型再进行5 个工况的计算分析;并将计算结果与试验结果的相对误差进行比对,得到5 组相对误差的平均值相对于α的变化关系(如图5所示)。由图可以看出,随着α从0 到1 的变化过程,热流密度的相对误差先减小、后增大。其中α在0.75~0.90 之间时,相对误差降到20%以下。这个α的取值范围与2.3 节利用理论经验公式讨论所得的结果一致。α为0.8 时计算结果的相对误差最小,约为7.17%,以该α的取值作为模型修正的5 种工况下热流密度计算结果及相对误差见表4。可以看到,除了工况2,其他4 个工况的相对误差均在5%以下。

表4 不同模型计算结果与MBB 试验结果对比Table 4 The comparision between MBB experimental results and simulation results for different models
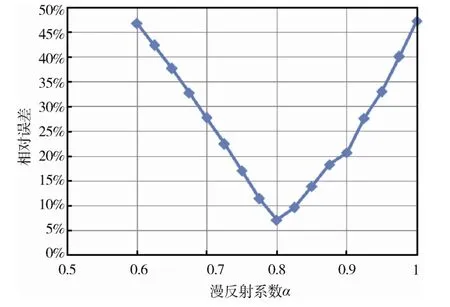
图5 计算结果与试验结果相对误差随漫反射系数 α 的变化Fig.5 The variation of relative error between experimental and simulation results against accomodation ratio α
为了进一步验证修正后Knudsen 模型的有效性,利用α=0.8 的修正模型分别计算了距10 N 推力器喷口的距离R=55 cm 处、在不同羽流角θ下的羽流热流密度值。以θ=0°为基准,将计算结果和 试验结果进行归一化后再对比,结果见表5和图6。
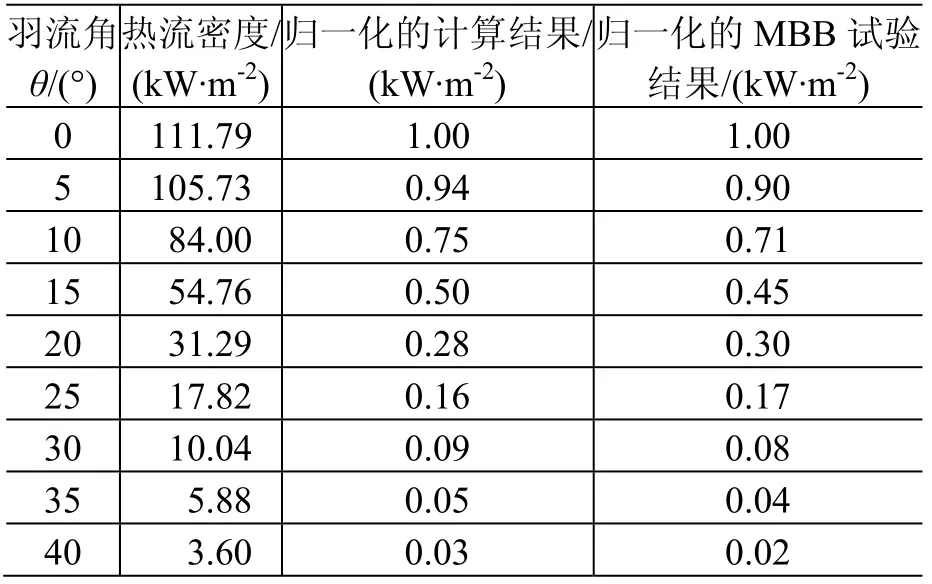
表5 数值仿真和MBB 10 N推力器试验的归一化结果比较Table 5 The comparision between MBB experimental normalized results and numerical simulation normalized results
可以看出,无论是计算结果还是试验结果,在R不变的情况下,羽流热流密度均随着θ的增大而迅速减小,在趋势上表现出了非常好的一致性。整体上分析结果与试验结果吻合得较好,验证了修正后的Knudsen 模型的有效性。
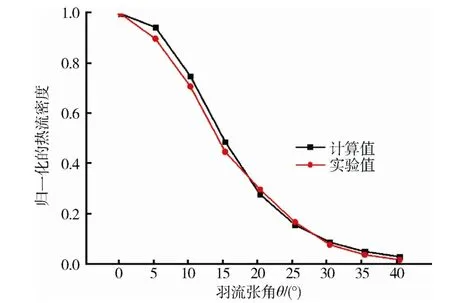
图6 推力器不同羽流角时热流密度计算结果与 试验结果对比Fig.6 The comparision between numerical simulation results and the experimental results at different plume flow angles
4 结束语
本文分析了Knudsen 模型中关键参数对羽流热效应计算结果的影响;并针对典型单组元和双组元推力器燃烧产物,讨论了模型中漫反射系数的取值范围;最后利用MBB 10 N推力器地面试验数据,采用遍历搜索的算法,对Knudsen 模型进行了修正,使得修正后的羽流热效应计算结果与试验结果的相对误差减小到约7%。相比保守的完全漫反射模型约50%的相对误差,修正后的模型大幅度地提高了羽流热效应计算的精度和可信度。
(References)
[1]Bird G A.Molecular gas dynamics and the direct simulation of gas flows[M].Oxford∶Clarendon Press, 1994∶2-4
[2]Gatsonis N A, Nanson R A, Lebeau G L.Simulations of cold-gas nozzle and plume flows and flight data comparison[J].Journal of Spacecraft and Rockets, 2000, 37(1)∶39-48
[3]Ebrahimi H B.Numerical investigation of multi-plume rocket phenomenology, AIAA 1997-2942[R], 1997
[4]张建华, 蔡国飙.用Simons 法计算真空羽流[J].推进技术, 2002, 23(5)∶406-409 Zhang Jianhua, Cai Guobiao.Computation based on the Simons model for vacuum plume[J].Journal of Propulsion Technology, 2002, 23(5)∶406-409
[5]焦子龙, 庞贺伟, 杨东升.利用Simons 模型研究卫星 羽流污染[J].航天器环境工程, 2007, 24(3)∶160-163 Jiao Zilong, Pang Hewei, Yang Dongsheng.Application of Simons model for satellite plume contamination analysis[J].Spacecraft Environment Engineering, 2007, 24(3)∶160-163
[6]沈青.稀薄气体动力学[M].北京∶国防工业出版社, 2003∶228-230
[7]李志辉, 李中华, 杨东升, 等.卫星姿控发动机混合物羽流场分区耦合计算研究[J].空气动力学学报, 2012, 30(4)∶483-491 Li Zhihui, Li Zhonghua, Yang Dongsheng, et al.Coupled simulation of mixture plume for attitude-control satellite thruster[J].Acta Aerodynamica Sinica, 2012, 30(4)∶483-491
[8]梁杰, 阎超, 杨彦广, 等.过渡区侧向喷流干扰的并行DSMC 数值模拟研究[J].宇航学报, 2011, 32(5)∶1012-1018 Liang Jie, Yan Chao, Yang Yanguang, et al.Parallel DSMC simulation of lateral jet interaction in rarefied transitional region[J].Journal of Astronautics, 2011, 32(5)∶1012-1018
[9]Andrew D K, Dean C W, Muntz E P.Influence of gas-surface interaction models on predicted performance of a micro-resisitoje, AIAA 2000-2430[R]
[10]Thomas L B, Olmer F G.The accommodation coefficient of He, Ne, A, H2, D2, O2, CO2and Hg on platinum as a function of temperature[J].Journal of the Americal Chemical Society, 1943, 65∶1036-1043
[11]Goodman F O, Wachman H Y.Formula for thermal accommodation coefficient, AD631007[R], 1966
[12]Demirel Y, Saxena S C.Heat transfer in rarefied gas at a gas-solid interface[J].Energy, 1996, 21(2)∶99-103
[13]周志雄, 魏蔚, 汪荣顺.真空下气-固界面热适应系数的数值计算[J].低温与超导, 2007, 35(1)∶36-40 Zhou Zhixiong, Wei Wei, Wang Rongshun.The mathematic calculation of thermal accommodation coefficients at gas-solid interface in vacuum[J].Cryogenics and Superconductivity, 2007, 35(1)∶36-40
[14]孙宝祥.利用10N 推力器羽流试验数据建立羽流场数学模型[J].航天控制, 2005, 23(3)∶26-29 Sun Baoxiang.Modeling plume field using plume test data for 10N thruster[J].Aerospace Control, 2005, 23(3)∶26-29
[15]Trinks H.Evaluation of the exhaust plume of the bipropellant MBB 10N thruster for the INMARSAT2 satellite[C]//AIAA/ASME/SAE/ASEE 25thJoint Propulsion Conference.Monterey, CA, 1989.AIAA 89-2507

