供配电系统滤波器优化配置研究

罗进，杨月同，李志东，龙燕，冯平

（1. 301医院，北京100853；2. 后勤学院，北京 100858；3. 后勤工程学院，重庆 401311）

谐波在供配电系统中传输会导致设备电能消耗增加，使用寿命缩短，对供配电系统谐波进行研究，并通过优化采用经济合理的滤波器配置方案进行谐波治理显的尤为重要[1-3]。现有的谐波及滤波器优化配置研究基本都是针对35 kV或10 kV中压系统进行的，还没有对0.4 kV低压配电系统的研究。低压设备间的谐波污染是否得到了很好治理并不清楚；滤波器优化配置大多是对PPF或APF单独进行的，两者同时优化的研究很少，几乎没有综合考虑PPF、APF和HAPF 3种滤波器的优化；滤波器配置位置往往只在谐波源节点选取，在同时存在多个谐波源的系统中不一定是最佳位置[4-6]。因此，采用有效的优化方法在所有节点上对PPF、APF和HAPF 3种滤波器配置位置和类型进行优化，使得谐波治理效果更好，投资费用更少，有着重要的理论意义和实用价值。

1 滤波器

常见的滤波器可以分为有源、无源和混合3种，都有着各自的优缺点。其中无源滤波器因其结构简单，价格低廉而得到了广泛的应用[7]；有源滤波器虽然滤波效果更理想，但价格昂贵，结构复杂[8-9]；混合滤波器综合了无源和有源的优点，是一种理想的滤波器，但其技术起步较晚，目前仍是人们研究的热点问题之一。文中无源滤波器（PPF）由若干个单调谐滤波器和高通滤波器构成。有源滤波器（APF）选用技术较成熟，使用较多的并联型有源滤波器，它按一定比例QUOTE吸收节点的谐波电流；混合型有源滤波器（HAPF）选用由PPF与APF并联所构成的并联型混合滤波器[10-15]。

2 谐波潮流计算

在基波潮流计算方面，本文采用应用最为广泛的牛顿-拉夫逊法，它具有二阶收敛特性，其核心是反复求解修正方程并修正变量[16-17]；谐波潮流计算方面，利用现场测量谐波数据，采用改进的解耦算法，通过求解变形的系统网络方程Uh=Y－1hIh得到节点各次谐波电压[18]，避免了忽略基波和谐波相互影响，模型建立不精确等带来的偏差，使计算结果更贴近实际，更精确。

3 遗传算法

3.1 个体编码

本文中将优化的解个体表示为X=［x1，x2，…，xi，…，xn］。其中，xi为节点i对应的滤波器安装情况，采用0、1、2、3编码，分别为第i节点不安装滤波器、安装PPF、安装APF、安装HAPF。

3.2 目标函数

滤波器优化配置目标函数为：

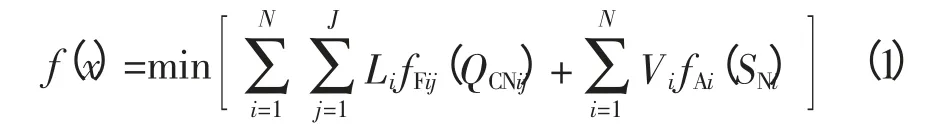
式中，N为系统总节点数；J为节点i安装的无源滤波器支路数；Li，Vi为是否安装滤波器参数，其值由xi决定；QCNij为节点i安装的PPF第j条支路电容器额定容量；SNi为节点i安装的APF额定容量；fFij（QCNij）为PPF费用与电容器容量的函数关系，如式（2）所示；fAi（SNi）为APF的费用与容量的函数关系，如式（3）所示。式中a0，a1，b1均为系数，分别为无源滤波器固定费用、电容器单位容量价格和有源滤波器单位容量价格[4]，其值由市场价格确定，本文在市场调研的基础上对其的取值如表1所示。

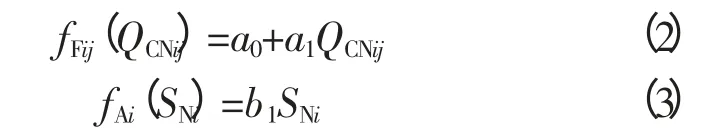
表1 滤波器价格参数取值Tab. 1 The price parameter of the filter

3.3 约束条件及违反约束的处理

本文以国家标准GB/T 14549-1993 和GB/Z 17625-2003对0.4 kV电压等级电网的电压总谐波畸变率限值为约束条件，如式（4）所示，式中THDUi为节点i的电压总谐波畸变率，cTHDU=5%为国家标准规定限值。对于违反约束条件的个体采用直接加惩罚值的形式改变其畸变率，而从降低其个体适应度值。惩罚函数如式（5）所示，其中c为惩罚系数，根据根据多次运行数据统计取最优值为100。

4 优化配置程序

本文利用MATLAB遗传算法工具箱实现了对滤波器配置类型和位置的优化，工具箱提供了很好的人机界面，可以方便地对遗传算法的适应度函数、线性和非线性约束、变量个数等参数进行设置。最后，将Matlab软件编写的牛顿拉夫逊法基波潮流计算程序，改进解耦法谐波潮流计算程序，滤波器参数计算程序和遗传算法优化程序进行整合，实现了对3种类型滤波器的统一优化配置，总的优化配置程序流程图如图1所示。

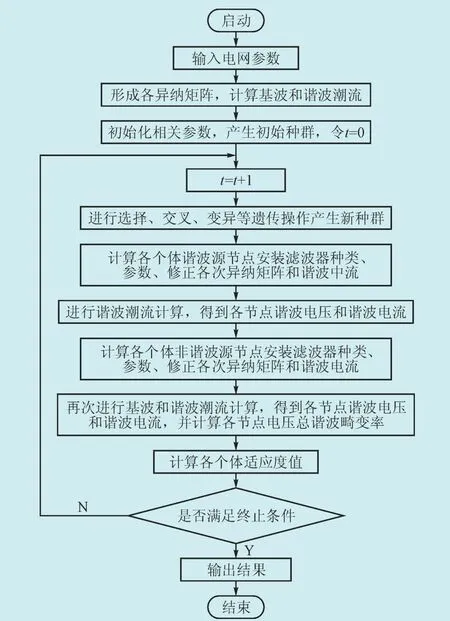
图1 遗传算法优化滤波器配置程序流程图Fig. 1 The flow chart of genetic algorithm to optimize the filter configuration program

5 算例分析

算例以某医院配电系统为背景，其拓扑图如图2所示。由于谐波源分布较广，系统中7、9、11、13、15、17、19、22、24、25、27、28、29节点均为谐波源节点，它们向系统注入3～19次奇次谐波。系统线路、负荷及谐波电流参数参见文献[19]。

5.1 优化配置结果

通过所编写的滤波器优化配置程序对算列进行计算，经过72代遗传得到了最优配置方案，总投资金额为53.7万元。图3为最优结果的遗传算法收敛示意图，其中：图3（a）为每代个体适应度值中的最小值（best penalty value）和平均值（mean penalty value）；图3（b）为优化得到的最优个体（current best individual），即最优配置方案；图3（c）为最优种群各个体的适应度值分布柱状图（score histogram）；图3（d）为最优种群100个个体的适应度值。具体的滤波器配置情况如表2所示，图4为安装滤波器前后各节点谐波畸变率变化示意图。

图2 配电系统拓扑示意图Fig. 2 Distribution system topology diagram

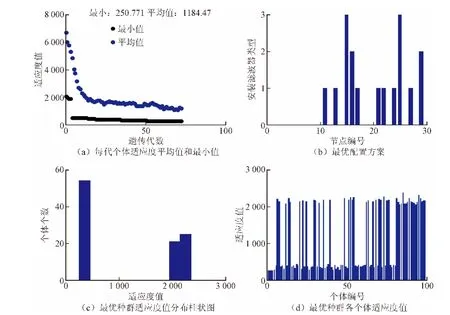
图3 遗传算法最优结果收敛示意图Fig. 3 Convergence diagram of achieving the optimal result by the genetic algorithm

图4 配置波器前后各节点电压总谐波畸变率变化示意图Fig. 4 The THDU changes before and after the filter is installed

5.2 优化配置结果对比

单一配置PPF、APF、HAPF 3种滤波器和仅在变压器高低压侧、谐波源节点优化配置结果与本文方法所得结果的对比如表3所示，由表可知在系统所有节点统一优化配置3种滤波器的投资费用更少，且谐波治理的效果也更理想。

6 结语

本文在总结滤波器优化配置研究现状的基础上，建立相应数学模型，编写相关程序，并基于MATLAB遗传算法工具箱实现了对PPF、APF、HAPF 3种滤波器在供配电系统所有节点安装类型和位置的优化。对算例进行滤波器优化配置，结果明显优于以往常用方法，治理前后谐波畸变率变化显著，达到了很好的治理效果，可以有效减少滤波器投资费用，验证了所采用方法的合理有效性和编写程序的正确性。

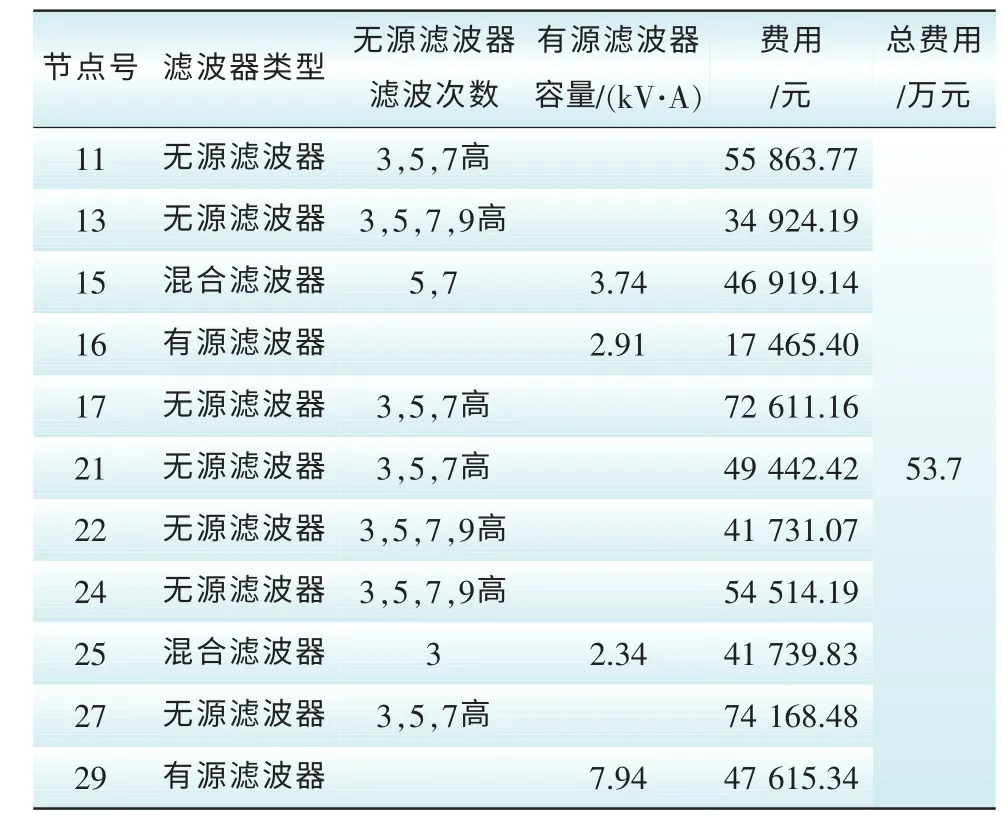
表2 滤波器安装节点及参数Tab. 2 The installation node and parameter of HAPF

表3 不同配置方式优化结果Tab. 3 The results of different types of optimization configuration

[1] 宋鹏超，王金全，李建科，等. 非线性负荷谐波模型研究综述[J]. 电工电气，2012（8）: 1-4.SONG Pengchao，WANG Jinquan，LI Jianke，et al. Study review of harmonic model of non-linear loads[J]. Electrical Equipment，2012（8）: 1-4（in Chinese）.

[2] 张铁龙，徐公林，桃霞. 谐波抑制与滤波装置的应用[J].电气开关，2009（4）: 75-78.ZHANG Tielong，XU Gonglin，TAO Xia. Harmonic suppression and application of filter devices[J]. Electrical Switch，2009（4）: 75-78（in Chinese）.

[3] 李圣清，罗飞. 电力谐波研究现状及综合治理方法综述[J]. 湖南工业大学学报，2007，21（1）: 74-78.LI Shenqing，LUO Fei. The overview of current situation research and comprehesive treatment for electric dynamic harmonic[J]. Journal of Hunan University of Technology，2007，21（1）: 74-78（in Chinese）.

[4] 李春莹. 基于多谐波源负荷动态运行的配电网络滤波装置优化配置[D]. 西安：西安理工大学，2005.

[5] 林至清. 基于网络固有结构法的多谐波源配电网滤波装置的分级优化研究[D]. 成都：四川大学，2006.

[6] 李习武. 配电网的无源滤波器优化配置的研究[D]. 北京：中国石油大学，2008.

[7] 熊来红，陈伟，刘兴栋，等. 电网可视化无源滤波器优化设计软件开发[J]. 电力电容器与无功补偿，2012，33（4）: 25-33.XIONG Laihong，CHEN Wei，LIU Xingdong，et al. Development of optimal design software for visualization passive power filter of power system[J]. Power Capacitor ＆ Reactive Power Compensation，2012，33（4）: 25-33（in Chinese）.

[8] 熊来红，陈伟，刘兴栋，等. 电网可视化无源滤波器优化设计软件开发[J]. 电力电容器与无功补偿，2012，33（4）: 25-33.XIONGH Laihong，CHEN Wei，LIU Xindong，et al.Development of optimal design software for visualization passive power filter of power system[J]. Power Capacitor &Reactive Power Compensation，2012，33（4）: 25-33.

[9] 吕敬，高宁，蔡旭. 基于复合控制的并联有源滤波器的仿真研究[J]. 高压电器，2012，48（3）: 81-85.L譈Jing，GAO Ning，CAI Xu. Simulation study of shunt active power filter based on compound control[J]. High Voltage Apparatus，2012，48（3）: 81-85（in Chinese）.

[10] 陈洁，曾旭华，姜建勋，等. 变电站微机电源防雷滤波器的设计研究[J]. 电瓷避雷器，2013，21（1）: 84-88.CHEN Jie，ZENG Xuhua，JIANG Jianxun，et al. The design and research of the substation computer power supply prevents thunder filter[J]. Insulators and Surge Arresters，2013，21（1）: 84-88（in Chinese）.

[11] 侯冲，肖铁军，范岩，等. 并联型有源电力滤波器的Matlab仿真研究[J]. 电网与清洁能源，2013，29（9）: 11-17.HOU Chong，XIAO Tiejun，FAN Yan，et al. Research on shunt active power filter with matlab simulation[J]. Power System and Clean Energy，2013，29（9）: 11-17 （in Chinese）.

[12] 任军辉，张万荣，张帆，等. ±1 100 kV直流输电工程直流滤波器方案研究[J]. 高压电器，2013，49（3）: 69-72.REN Junhui，ZHANG Wanrong，ZHANG Fan，et al.Study on ±1 100 kV HVDC project DC filter scheme[J].High Voltage Apparatus，2013，49（3）: 69-72.

[13] 任军辉，张万荣，孙伟，等. 特高压直流输电工程直流滤波器故障仿真[J]. 高压电器，2013，49（1）: 50-52.REN Junhui，ZHANG Wanrong，SUN Wei，et al. Simulation on UHVDC project DC filter faults[J]. High Voltage Apparatus，2013，49（1）: 50-52.

[14] 袁浩悦，曹以龙. 有源电力滤波器的谐波检测研究[J].电力电容器与无功补偿，2012，33（5）：17-22.YUAN Haoyue，CAO Yilong. Research on harmonic detection of active power filter[J]. Power Capacitor & Reactive Power Compensation，2012，33（5）：17-22.

[15] 夏玉印，刘少华，陈灵奎. 一种实用新型的并联混合有源滤波器研究[J].电力电容器与无功补偿，2012，33（5）：45-49.XIA Yuyin，LIU Shaohua，CHEN Lingkui. Research of a practical and new type shunt hybrid active power filter[J].Power Capacitor & Reactive Power Compensation，2012，33（5）: 45-49.

[16] 李洪波. 电力系统谐波潮流计算算法综述[J]. 重庆电力高等专科学校学报，2004，99（3）: 1-4.LI Hongbo. A summary for power system harmonic flows calculation[J].Journal of Chongqing Electric Power College，2004，99（3）: 1-4（in Chinese）.

[17] 孙媛媛，王小宇，尹志明. 多谐波源系统的非迭代式谐波潮流分析[J]. 中国电机工程学报，2012，32（7）:83-90.SUN Yuanyuan，WANG Xiaoyu，YIN Zhiming. Noniterative harmonic power flow analysis for power systems with multiple harmonic sources[J]. Proceedings of the CSEE，2012，32（7）: 83-90（in Chinese）.

[18] 卢恩，张步涵，龚世缨. 电力系统谐波潮流的一种解耦算法[J]. 电网技术，2003，27（2）: 34-36.LU En，ZHANG Buhan，GONG Shiying. A decoupled algorithm for power system harmonic flows[J]. Power System Technology，2003，27（2）: 34-36（in Chinese）.

[19] 李志东. 医院配电系统谐波及滤波器优化配置研究[D].重庆：后勤工程学院，2014.