一种低频振荡机组参与程度在线识别方法

魏亚婷，余一平，孙冉，孙建华，熊浩清

（1. 河海大学 能源与电气学院，江苏 南京 210098；2. 河南电力调度控制中心，河南 郑州 450052）

随着电网规模的日趋庞大和区域电网互联工程的实施，局部的扰动会引发许多弱互联系统发生低频振荡，因此低频振荡已成为威胁互联大电网安全稳定运行的突出问题[1-6]。发电机组作为低频振荡的主要参与者，及时识别其参与程度至关重要。目前低频振荡比较常用的分析方法是模态分析法。通过模态分析可以判断系统中存在哪些局部振荡模式和区间振荡模式，是否为弱阻尼模式，各模式的强相关机组有哪些，同时还可以计算特征值与系统参数间的灵敏度关系[7-8]。由于模态分析法提供的信息量多，它已成为多机电力系统低频振荡分析最有效的方法之一。以往低频振荡中的机组参与程度通常用模态分析获得的线性参与因子来评估。但是模态分析方法的计算结果与系统模型参数的精度有关，且计算速度慢，误差较大，不能满足低频振荡在线分析及实时系统的快速紧急控制的需要[9-10]。WAMS技术的快速发展和广泛应用为电力系统低频振荡的在线分析提供了新的数据基础。以往Prony等辨识方法应用于系统振荡模式在线辨识方面取得了很大进展，但如何在线评估机组的参与振荡程度尚存在不足[11-13]。

自然界中能量是体现运动强弱的一种方式，可以反映运动的特性[11]。而低频振荡是电力系统一种特殊的运动形式，振荡过程中同样伴随着振荡能量的传播和交换[14-15]。基于机组振荡能量的分布，可以了解低频振荡运动特性，评估各振荡机组的参与程度。本文研究采用模态能量的方法分析电力系统的低频振荡问题，通过WAMS动态信息根据振荡模态能量在线确定系统的强相关机组[16-18]。首先基于线性化电力系统状态方程，引入描述电力系统振荡能量的模态能量方法，在分析传统模态分析结果与振荡能量之间的相关性基础上，提出了基于模式动能参与因子在线识别机组参与程度的方法，并通过四机两区系统与10机39节点系统的分析，验证方法的合理性与可行性。

1 电力系统线性表示

在包含n台发电机的多机系统中，其线性化的n维状态方程为[8]

式中，x为系统增量形式的状态矢量；A为系统的系数矩阵；u为外部扰动输入向量；B为相应系数矩阵。

式中，xω=[Δω1r，Δω2r，…，Δωnr]T是相对转子角速度子向量；xδ=[Δδ1n，Δδ2n，…，Δδn-1n]T是相对角子向量；xz其他系统变量向量。

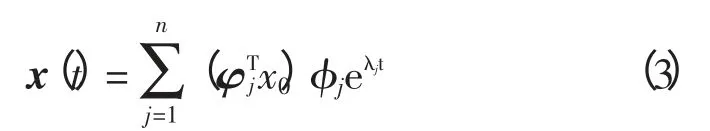
式中，λj（j=1，…，n）是系统特征值，准j，φj是右左特征相量。归一化左右特征相量关系为

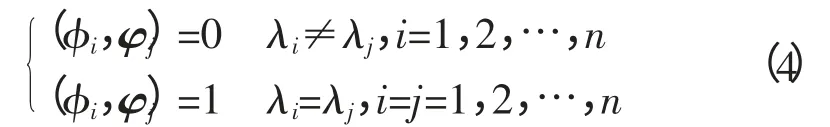
2 模态能量方法的基本原理

在包含n台发电机的多机系统中，发电机采用经典二阶模型（假定E’恒定），状态方程为

对应的常系数齐次线性微分方程为

采用模态坐标，令x=准z，左右特征向量分别为φ和准。第i个状态量可表示为[12]：

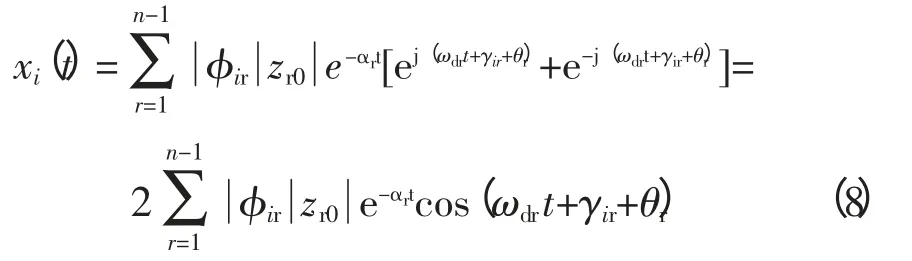
第i台机组的动能可以表示为

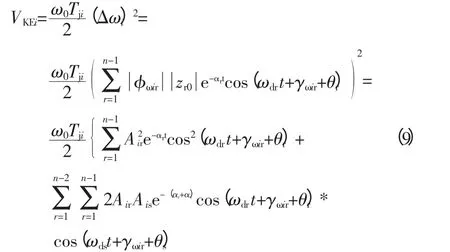
定义机组模式动能为

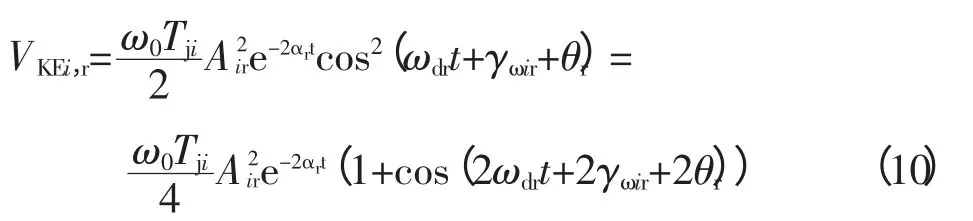
为分析方便，仅考虑含有单个弱阻尼主导模式的情况，此时模式动能VKEi，r为机组主要振荡能量的体现。以各个机组模式动能的振荡幅值，即振荡过程中机组具有的最大模式动能值作为机组参与振荡的评价标准，即可以从能量的角度分析机组在低频振荡中的参与程度。

定义单个模式下机组的模式动能参与因子

在多机系统情况下，可以将与第r阶振荡模式λr相关的左右特征向量分别表示为转子角偏差和转速偏差对应的向量形式，即ψTr=[ψTδrψTωr]和准r=[准δr准ωr]T。

文献[13]通过模态分析证明了在采用电力系统经典模型，不考虑网络电阻和发电机阻尼的情况下，左右特征向量存在如下关系

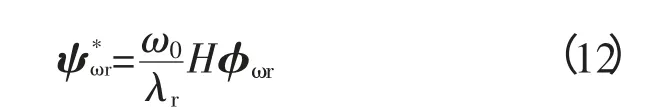
将式（9）代入式（8），则

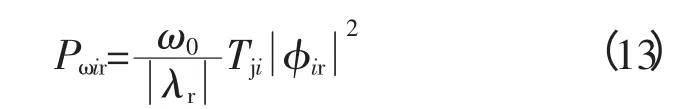
在低频振荡离线分析中，基于模态分析所得到的线性参与因子为，其为左右特征相量的乘积，既包含了状态变量xi对λi的可观性，也包含了对λi的可控性，它是确定与各个模式强相关的系统变量的有效途径[13]。但是在低频振荡在线分析中，观测获得的Δω和Δδ的相对大小与右特征相量元素的相对大小相一致，而左特征相量所含有的可控信息很难获得，因此常常用右特征相量来识别强相关机组，但这种方法只是从可观性角度出发。实际系统中，各台发电机的惯性时间常数相差较大，且右特征相量中各元素的相对大小只是反映了各机组角位移的相对大小，并没有准确反映各机组在不同模式下振荡过程中参与程度的大小。而模式动能则体现了不平衡转矩对角位移做功的大小，从能量的角度分析机组在低频振荡中的参与程度。

线性参与因子是由线性模式分析法得到的，与系统的结构相对应，必须依赖于系统模型和参数，适用于离线分析，难以准确在线获得。而由公式（10）可知，模式动能法中模式动能参与因子，可以通过实际运行监测的WAMS观测状态量动态信息Δω和机组惯性时间常数Tj计算获得，不受系统结构和模型准确性的影响，精确且方便[12，14-15]。

3 算例分析

3.1 四机两区域系统算例

以四机两区域系统为例，采用发电机经典模型，发电机阻尼系数设置为0，网络结构为纯电感。用BPA软件搭建模型和MATLAB[19]计算结果如下：

由表2可知，模态1是区间振荡，此模式为机组1、2和机组3、4之间存在能量交换；4台机组的线性参与因子幅值大小排序为机组3>机组4>机组2>机组1。线性参与因子的幅值越大，则机组参与该模式的程度越大。4台机组的能量参与程度分别为机组3>机组4>机组2>机组1，即模式动能因子参与度排序与线性参与因子参与度排序完全一致，而模式动能因子则从能量角度反映机组在该模式下振荡中的参与程度。由表3可知即模态2是机组1与机组2之间存在能量交换的区域内振荡；由表4可知模态3是机组3与机组4之间存在能量交换的区域内振荡。

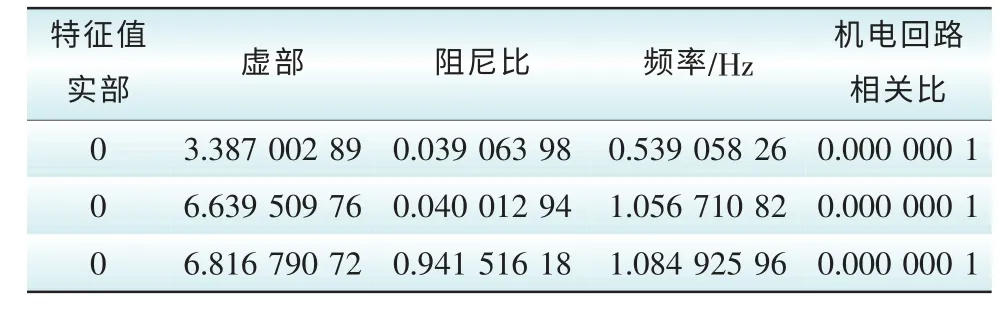
表1 四机两区域系统经典模型模态分析结果Tab. 1 The modal analysis of 4-machine 2-area system with the classic model

表2 四机两区域系统模态一下各机组参与因子及参与度Tab. 2 Participation factor and its sorting in modal 1 of 4-machine 2-area case

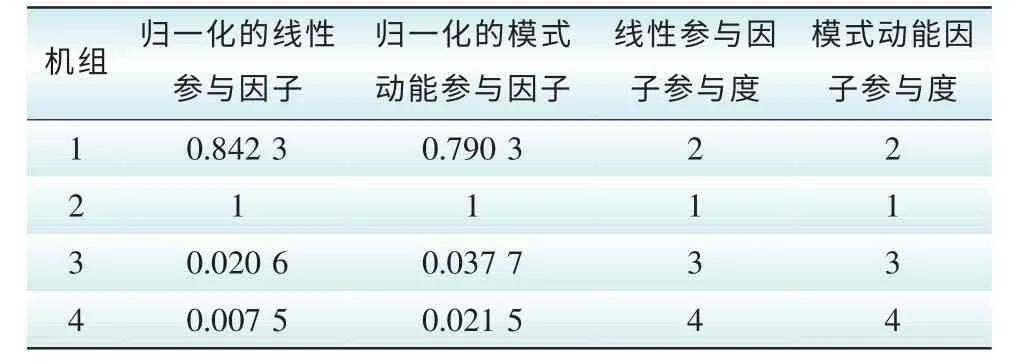
表3 模态二下各机组参与因子及参与度Tab. 3 Participation factor and its sorting in Mode 2

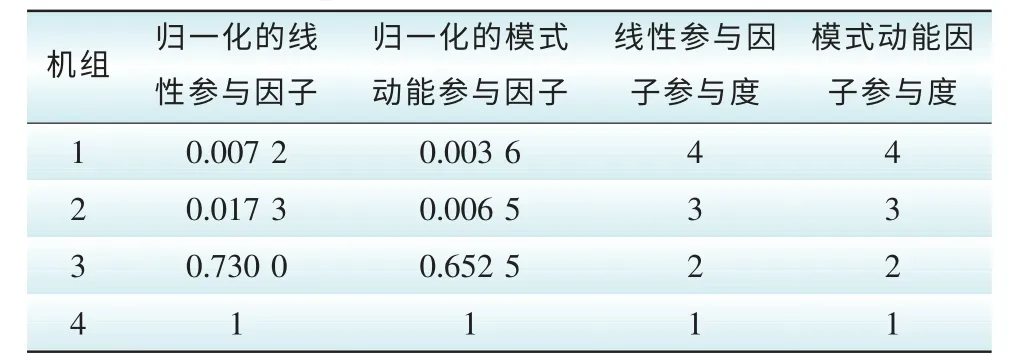
表4 模态三下各机组参与因子及参与度Tab. 4 Participation factor and its sorting in Mode 3

即在纯阻抗网络结构和发电机阻尼为0的情况下，单个振荡模式下机组转速偏差对应的线性参与因子与模式动能参与因子排序完全一致。实际的电力系统结构较为复杂，需要考虑网络电阻和系统阻尼等因素。因此四机两区域系统发电机应采用详细模型，且考虑线路电阻。但是机组模式动能参与因子和线性参与因子还是应该存在近似的对应关系。机组模式动能可以通过WAMS动态信息在线观测或者计算得到，这为系统在线监测量与模态分析结果间建立一种关系，则采用模式动能参与因子从振荡能量角度在线确定强相关机组，为在线识别强相关机组提供了新的方法。

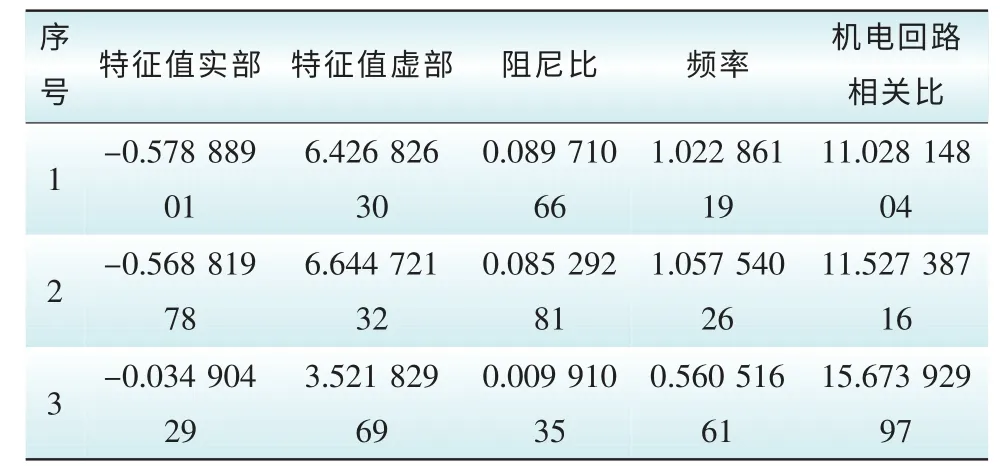
表5 四机两区域详细模型模态分析结果Tab. 5 The modal analysis of 4-machine 2-area system with the detailed model

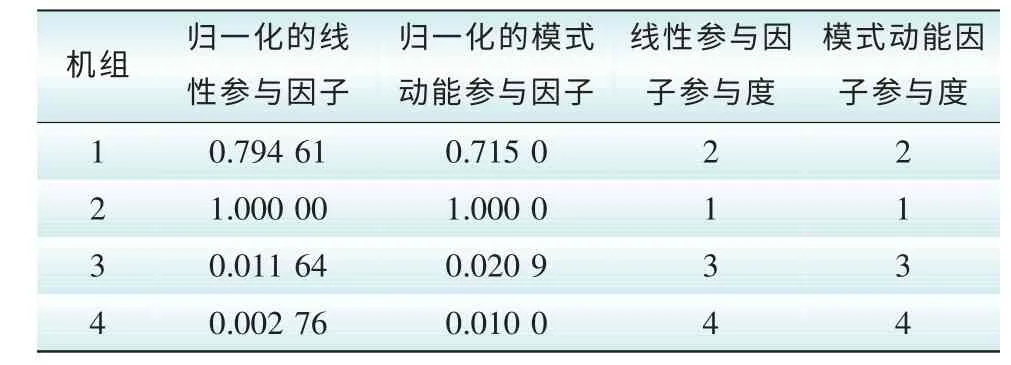
表6 模态一下各机组参与因子及参与度Tab. 6 Participation factor and its sorting in Mode 2

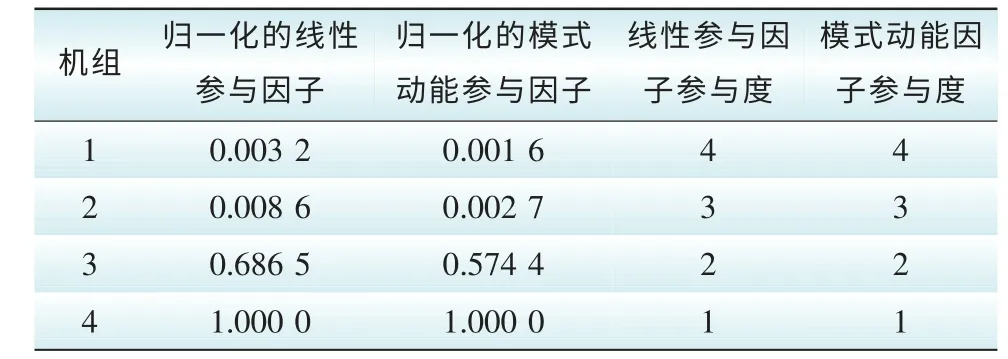
表7 模态二下各机组参与因子及参与度Tab. 7 Participation factor and its sorting in Mode 2

由表6—表8可知，四机两区域系统在考虑网络电阻及发电机阻尼的情况下，3个模态下计算得到的线性参与因子与模式动能因子参与度排序一致，这说明了模式动能可以在线识别强相关机组。

3.2 新英格兰10机39系统算例

由表10知，线性参与因子参与度排序与模式动能因子参与度排序完全一致。

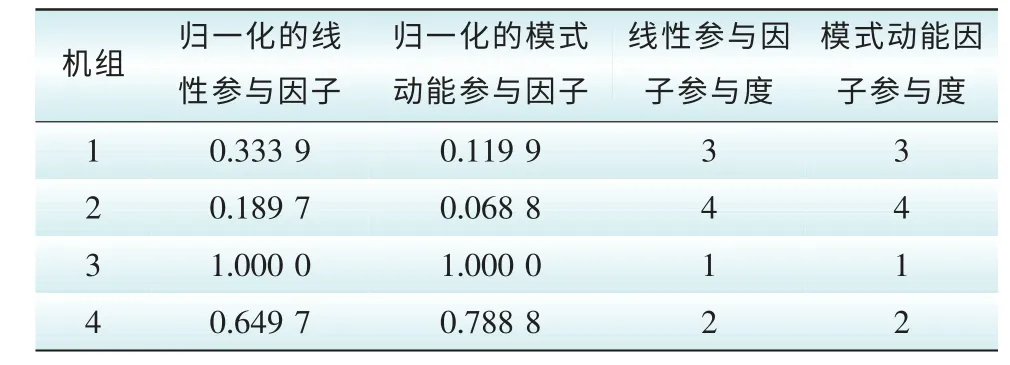
表8 模态三下各机组参与因子及参与度Tab. 8 Participation factor and its sorting in Mode 2

表9 10机39节点系统模态分析结果Tab. 9 The modal analysis of IEEE 10-machine 39-bus system

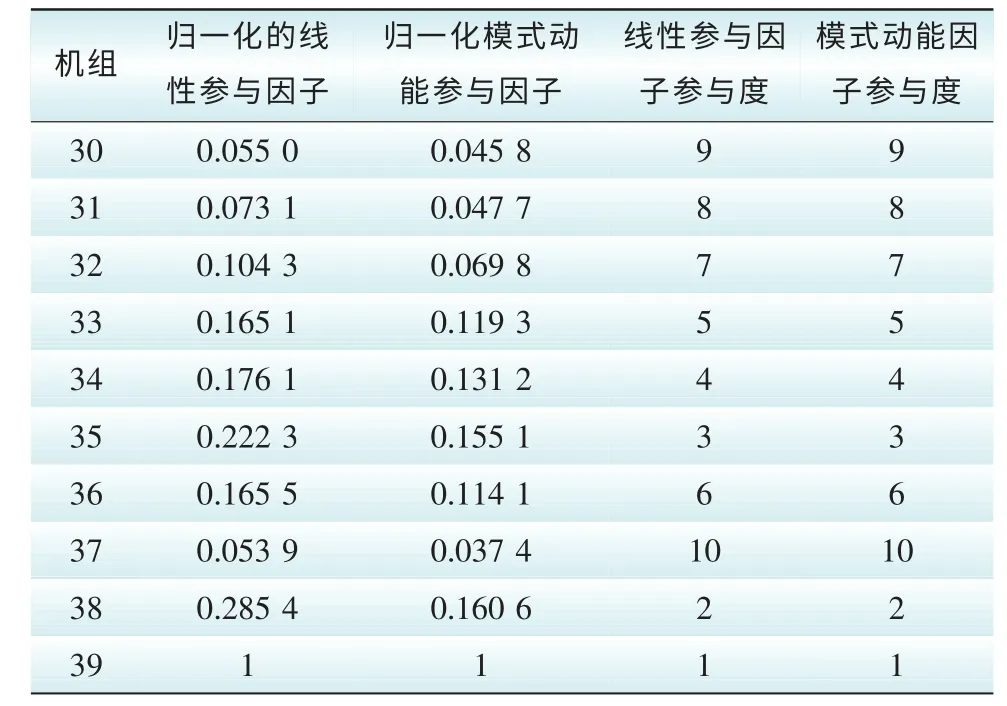
表10 模态9下各机组参与因子及参与度Tab. 10 Participation factor and its sorting in Mode 9

为增加结果的可信度，再选择一个模态，即阻尼比最小、频率较小的第七个特征值对应的模态进行研究。在此模态下，机组1与机组8之间存在能量交换。

从表11可以看出，此模态中，除了两台机组的两种参与因子的排序不同，其余所有模态下所有机组两种参与因子的排序均相等。并且，即使是在这两种情况下，两台机组两种排序也仅仅相差一位，这足以说明，两种方法所得到两种因子的结果是基本一致的，都是与机组在该模态下对能量的贡献成正比的。

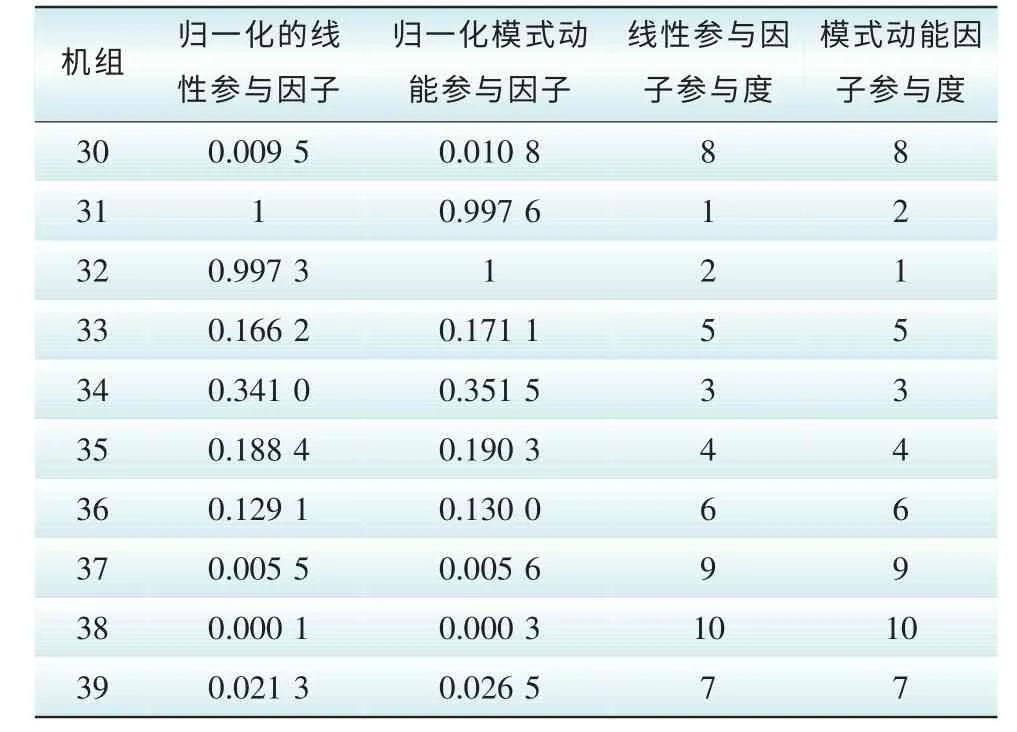
表11 模态7下各机组参与因子及参与度Tab. 11 Participation factor and its sorting in Mode 7

前文已经通过理论证明，在网络结构为纯感性和阻尼为零时，线性参与因子是与该模态下机组的动能成正比的。而上述的算例中，无论是在四机两区域还是新英格兰10机39节点的系统中，在系统阻尼为零时，能量模态法与线性模式分析法所计算出的2种因子极为接近，因为此种情况下线性模式分析法得出的线性参与因子与系统动能直接成正比，则存在能量交换的机组的模式动能参与因子与能量之间存在高度的正相关。这从侧面反映了模态分析法中模式动能参与因子是对能量关系准确的反映。

3.3 机组阻尼改变对线性参与因子与能量间关系的影响

在阻尼为零的情况下，线性参与因子与该模态下每台机组对于模态动能的贡献成正比。下面将改变系统中发电机的参数D，从而改变发电机组的阻尼进而改变系统阻尼。验证D的改变是否对应着系统阻尼的改变。在改变阻尼的情况下，算出每一个阻尼对应的两种参与因子，并计算其相关性，从而证明不同阻尼下同一机组两种参与因子的相关性，即阻尼的变化与线性参与因子与能量之间的相关性。

在这一部分，同步改变每一台机组的D，计算出每一个D对应的第一台机组在模式1下的两种参与因子，并且计算两种因子的相关系数。

由表12可知，随着D的不断增大，阻尼比也不断变大，即系统阻尼随着发电机阻尼D的变大而变大。为了知道阻尼D改变后，4机2区域系统中4台机组的参与度是否有变化，表13列出了4机2区域系统模态一下，即区间振荡下两种因子的机组参与度排序。可以看出随着D的改变，2种因子的机组参与度都不变。模态2和模态3这2个区域内振荡下，机组参与度也不随着D的改变而发生变化。

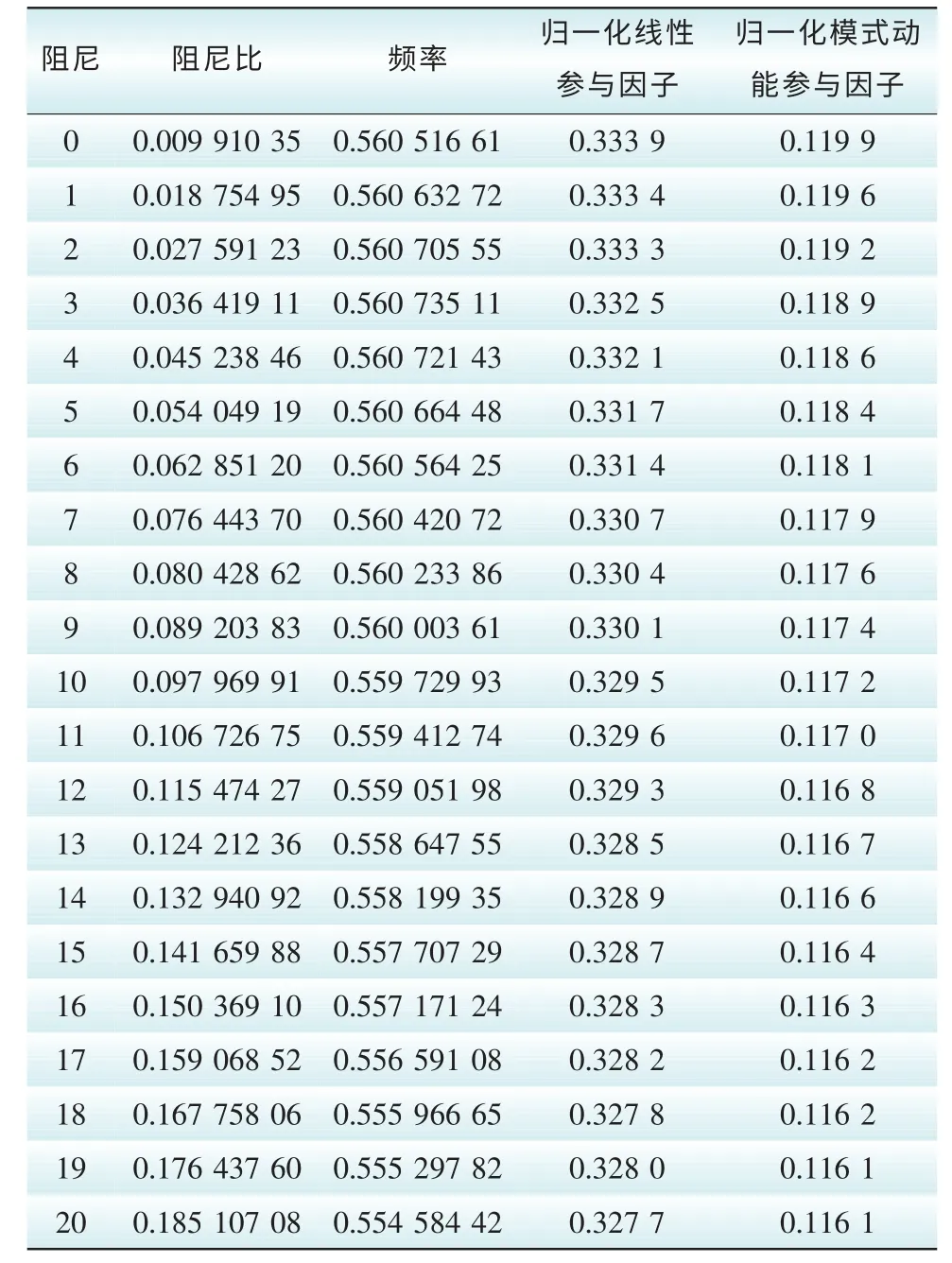
表12 D与同一机组两种参与因子的对应关系Tab. 12 The corresponding relation between D and two participation factors of the same machine

为了知道两种因子的相关性，本文作了两种因子的散点图，并且运用数学统计工具计算其相关性。

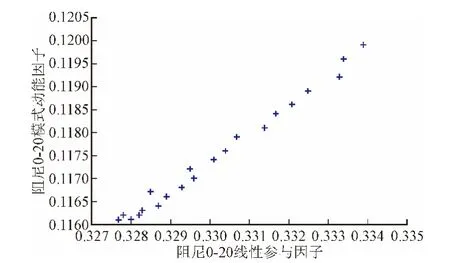
图1 不同D的两种因子散点图Fig. 1 The scatter diagram of two factors of different D

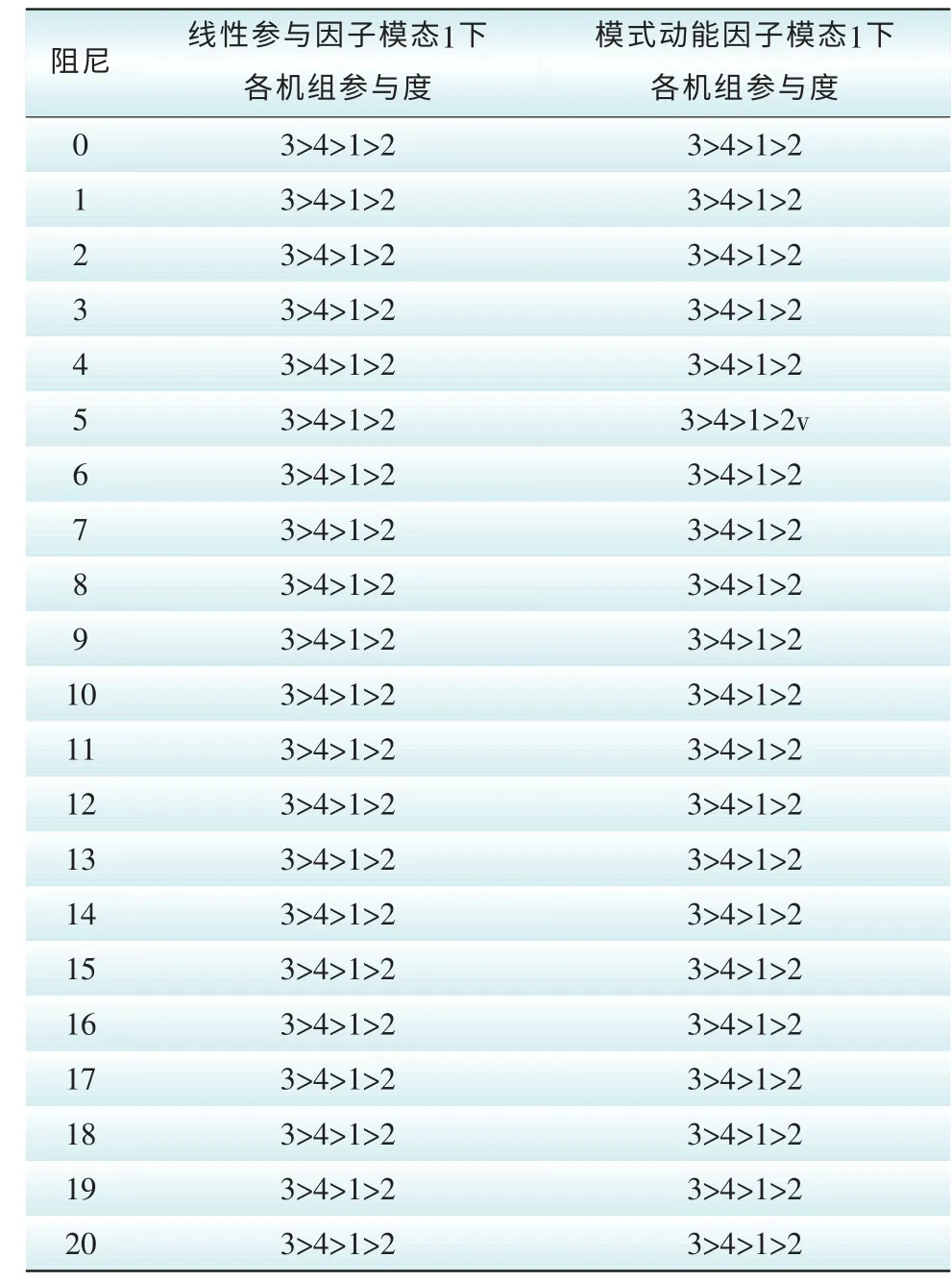
表13 四机两区域模态一下不同D的2种因子的机组参与度Tab. 13 The participation unit of two factors with different D in modal 1 of 4-machine 2-area case

通过统计工具，可以计算出这两列数据的皮尔逊相关系数（积差相关系数）为0.980，说明了21例样本中线性参与因子与模式动能因子之间存在正相关关系，因为数据为21组，自由度为df=21-2=19，则相关系数检验表中α=0.01的临界值为0.449。也就是说，两组数据是正相关的，在0.01水平上显著相关。证明了存在能量交换的机组的模式动能参与因子之间存在高度的正相关，这从侧面反映了模态分析法中模式动能参与因子对能量关系的忠实而准确的反映。

这一结论验证了，阻尼一定程度上改变时，线性参与因子依然与模式动能因子近似地正相关，即线性参与因子也能在一定程度上反映能量关系，但这种关系不再是严格的一一对应。

4 结论

本文在回顾传统线性模式分析法的基础上，提出了模态能量分析方法，并定义模式动能参与因子来衡量机组在低频振荡过程中的参与程度。与传统的通过线性模式分析方法获得的线性参与因子确定强相关机组相比，线性参与因子必须通过模态分析计算获得，依赖于网络模型的准确性，而模式动能参与因子通过低频振荡时各机组的振荡能量相对大小判断强相关机组。由于各机组模式动能可以通过WAMS观测的动态数据直接计算获得，因此该方法可以应用于低频振荡机组参与程度的在线识别。通过四机两区域系统和10机39系统线性参与因子和模式参与因子的比较分析，验证了采用模式动能识别机组参与程度的合理性。这种方法突破了以往模态分析要先了解系统结构才能进一步分析的局限性，也不再受制于系统规模和参数的准确性。

[1] 韩志勇，李志强，李莹，等. 汽轮机调速系统引起电力电力系统共振机理低频振荡扰动分析[J]. 陕西电力，2009，37（7）: 1－5.HAN Zhiyong，LI Zhiqiang，LI Ying，et al. Power system low frequency oscillation of resource mechanism induced by disturbance of turbine-governing system[J]. Shaanxi Electric Power，2009，37（1）: 1－5（in Chinese）.

[2] 吴复霞. 电力系统低频振荡的分析和控制[D]. 杭州: 浙江大学，2007.

[3] 关海平，焦晓亮. 600 MW汽轮发电机组运行状况的调研分析[J]. 节能技术，2011，29（1）: 57－65.GUAN Haiping，JIAO Xiaoliang. Study and analysis on operating conditions of 600 MW turbo-generator sets[J].Energy Conservation Technology，2011，29（1）: 57－65（in Chinese）.

[4] 朱亮. 自动发电控制在鲁布格水电厂的应用分析[J]. 西北水电，2014（1）: 71－73.ZHU Liang. Analysis on applications of automatic generation control in lubuge hydropower plant[J]. Northwest Hydroelectric，2014（1）: 71－73（in Chinese）.

[5] IEEE Power Engineering Society. Inter-area oscillations in power systems[J]. IEEE Publication 95 TP 101，IEEE，1995.

[6] 张秀坤，蒋明东. 国产600 MW汽轮机配汽方式优化改造[J]. 节能技术，2005，23（1）: 87－90.ZHANG Xiukun，JIANG Mingdong. Optimum governing of 600 MW turbine[J]. Energy Conservation Technology，2005，23（1）: 87－90.

[7] 倪以信，陈寿孙，张宝霖. 动态电力系统理论和分析[M].北京: 清华大学出版社，2002.

[8] 刘取. 电力系统稳定性及发电机励磁控制[M]. 北京: 中国电力出版社，2007.

[9] 刘春梅，李勇，辛杨，等. 电力系统低频振荡的影响因素研究[J]. 陕西电力，2011，39（6）: 12-15.LIU Chunmei，LI Yong，XIN Yang，et al. Study on influencing factors of low frequency oscillation of power system[J].Shaanxi Electric Power，2011，39（6）:12-15（in Chinese）.

[10] 张旭，沈沉，梅生伟，等. 小干扰稳定特征向量和相关因子的分布式算法[J]. 电力系统自动化，2007，31（14）:7－11.ZHANG Xu，SHEN Chen，MEI Shengwei，et al. Distributed algorithm for eigenvector and participation factor of small signal stability in power systems[J]. Automation of Electric Power Systems，2007，31（14）:7－11（in Chinese）.

[11] MESSINA A R，OCHOA M，BAROCIO E. Use of energy and power concepts in the analysis of the inter-area mode phenomenon[J]. Electric Power Systems Research，200，59（2）: 111－119.

[12] 余一平. 基于能量方法的电力系统低频振荡研究[D]. 北京: 清华大学，2010.

[13] CHAN S M. Small signal control of multiterminal dc/ac power systems[D]. Massachusetts Institute of Technology，1981.

[14] 王文标，尹冰玉，汪思源. 基于多种节能量模型的供热后评价研究[J]. 节能技术，2014，32（2）: 162－166.WANG Wenbiao，YIN Bingyu，WANG Siyuan. Research on post evaluation based on multiple energy saving[J].Energy Conservation Technology，2014，32（2）: 162－166（in Chinese）.

[15] 吴凯槟，彭旭东. 分布式能源面临重大发展机遇[J]. 节能技术，2013，31（5）: 437－441.WU Kaibin，PENG Xudong. Distributed energy faces significant development opportunities[J]. Energy Conservation Technology，2013，31（5）: 437－441（in Chinese）.

[16] 杨培宏，冯义，张遇杰. 基于广域测量系统的电力系统低频振荡抑制方法[J]. 陕西电力，2008，36（2）: 11－15.YANG Peihong，FENG Yi，ZHANG Yujie. Low-frequency oscillation damping method for power system based on wide-area measurement system[J]. Shaanxi Electric Power，2008，36（2）: 11-15（in Chinese）.

[17] 杨培宏，刘达. 基于广域测量系统的电力系统稳定器适配器方案[J]. 陕西电力，2009，38（4）: 11－14.YANG Peihong，LIU Da. Study of power system atabilizer configuration based on wide-area measurement system[J].Shaanxi Electric Power，2009，38（4）:11－14（in Chinese）.

[18] 刘东晖，钱乙卫，刘东英. WAMS在陕西电网的应用分析[J]. 陕西电力，2012，40（6）: 63－65.LIU Donghui，QIAN Yiwei，LIU Dongying. Application of WAMS in shaanxi power network[J].Shaanxi Electric Power，2008，36（2）: 11－15（in Chinese）.

[19] 陈虎，孟克其劳，马建光. 基于MATLAB的风力发电机组建模和仿真研究[J]. 节能技术，2012，30（1）: 24-28.CHEN Hu，MENG Keqilao，MA Jianguang. The modeling and simulation study of wind turbine based on matlab[J].Energy Conservation Technology，2012，30（1）: 24-28（in Chinese）.