基于光伏阵列建模的阴影多峰值电压估算
朱彬彬,杨勇,季爱民,曹丰文
(1. 苏州大学城市轨道交通学院,江苏 苏州 215006;2. 江苏省光伏发电工程技术研究开发中心,江苏 苏州 215104)
传统能源的枯竭以及环境问题的日益严峻,为绿色可再生能源的迅速发展提供了契机[1]。光伏发电被认为是继风力发电后最有潜力实现规模化发展和应用的可再生能源发电技术[2-3]。
然而由于光伏组件老化、工艺差异等内因,抑或者是因为云层、树木、建筑物等复杂环境在光伏阵列上形成不均匀阴影,导致光伏阵列光照强度不均匀,都会引起“故障”,使光伏组件输出功率大幅降低、甚至消耗其他组件产生的能量,导致局部过热,形成热斑效应。旁路二极管和阻塞二极管的引入,可以避免热斑效应的发生,但同时会导致阴影条件下光伏阵列输出特性存在多个峰值[4-6]。
局部阴影条件(partial shading condition,PSC)下光伏阵列的多峰值特性使得传统最大功率点跟踪(MPPT)策略失效的可能性升高,增大了光伏系统控制复杂性。为了提高光伏系统的发电效率,对阴影条件下光伏阵列建模,分析多峰值输出特性产生的原因很有必要,文献[7-11]对以上问题进行了研究。文献[7-8]基于不同的光伏电池等效模型分析阵列输出特性,模型参数多且大半与环境条件相关,难以测量,因而适用于理论分析。
文献[12]介绍了一种峰值电压的经验估算方法;文献[13]采用统计方法研究多峰值的分布规律;文献[7]直接将阵列的峰值电压和单串的峰值电压用相同符号标注,且未作具体说明。对阴影多峰值电压进行估算可以简化局部阴影条件下复杂的光伏模型,为多峰值MPPT提供思路,也可用于验证模型的正确性,揭示系统局部阴影条件下各参数间的联系。
本文采用文献[14]提出的工程方法,从简单情形入手,逐步深入,进而建立阴影条件下光伏阵列的通用模型。以此为基础,验证了阵列的峰值电压和单串的峰值电压间的关系,并提出一种基于光伏阵列模型的阴影多峰值电压估算方法。文章最后根据不同的阴影状况,对多峰值电压进行估算,验证方法的可行性。
1 光伏组件建模
图1是光伏电池的等效模型,可以看作是一个幅值为Iph的恒流源与二极管D并联,Iph称为光伏电池的光生电流,其大小与所处环境(温度、光照强度等)有关。Id是流过二极管D的电流,Upv和Ipv分别是光伏电池的输出电压和电流。Rsh为并联电阻,Rs为串联电阻,输出电流Ipv表示为[14]:
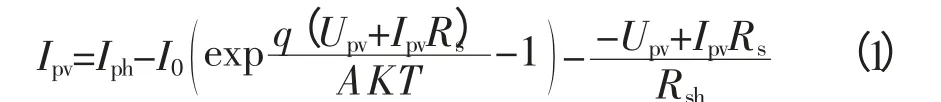
式中,I0为二极管反向饱和电流;q为电子电量,1.602×10-19C;K为玻尔兹曼常量,1.381×10-23J/K;T为光伏电池温度;A为二极管理想因子。
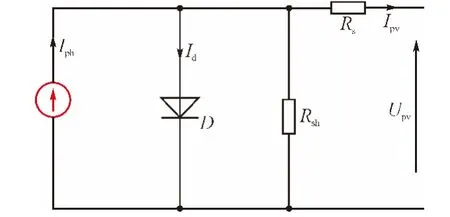
图1 光伏电池等效模型Fig. 1 The electrical equivalent circuit of a solar cell
光伏电池单体由于工作电压和电流较小,不具备实际应用价值。将光伏电池单体进行串并联封装后,成为光伏组件,功率在几十到数百瓦不等,是作为直流电源独立使用的最小单元。以下分析对象均为光伏组件。
由式(1)光伏电池I-U输出特性是一个超越方程,无法线性表出;Rsh、Rs、I0等受到多种因素影响,参数确定较困难。工程应用上采用非线性拟合等方法,对式(1)进行近似、简化处理[14-16]。以文献[14]工程方法为例:参考条件下,光伏组件短路电流Isc,开路电压Uoc,最大功率点电压和电流为Umpp、Impp,当光伏组件电压为Upv时,对应电流为Ipv:
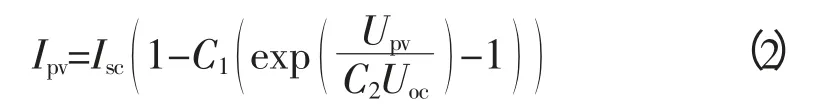
待定系数C1、C2由式(3)、(4)决定
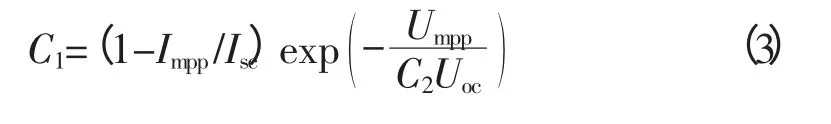

光伏组件输出特性会受到光照强度和温度的影响:在光照强度S和温度T条件下,假定输出特性形状基本不变,补偿系数推荐值α=0.002 5/℃,β=0.5,γ=0.002 88/℃。与标准条件Sref=1 kW/m2,Tref=25 ℃相比,组件各项参数变为:
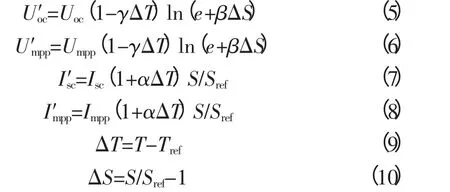
本文使用的光伏组件参数如表1所示。

表1 光伏组件参数Tab. 1 PV module parameters
2 阴影条件下光伏阵列建模
为了满足光伏发电系统功率等级和电压等级的要求,实际应用中将光伏组件进行串、并联组合,构成光伏阵列。本文将图2所示的由m个光伏组件串联组成的单元称为单串,将n个类似的单串进行并联,得到m×n光伏阵列。当不考虑环境变化以及各组件个体差异时,光伏阵列输出电流Iarray:
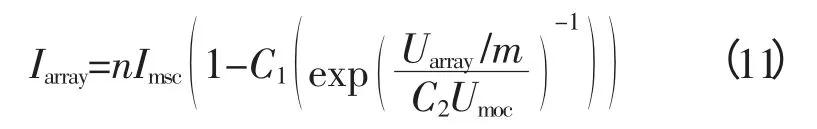
式中,Uarray和Iarray是光伏阵列输出电压、电流;Umoc和Imsc是光伏组件开路电压、短路电流。
在光伏组件两端并联旁路二极管,提供电流旁路,可以避免热斑效应的发生。此外,为了防止并联单串之间形成电流环路,导致能量逆流,各单串还需要串联阻塞二极管,为能量提供单向通路。图2对旁路二极管和阻塞二极管进行了标注。
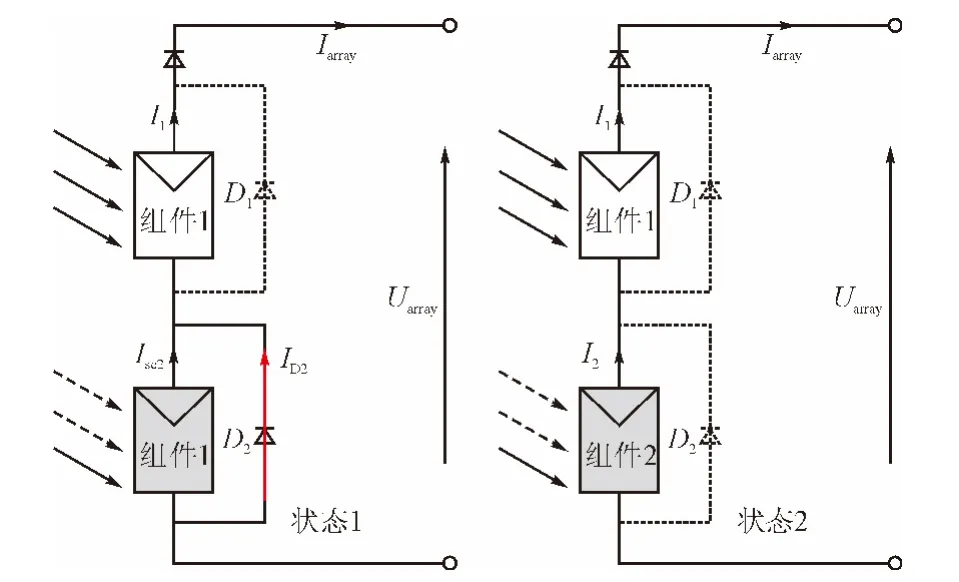
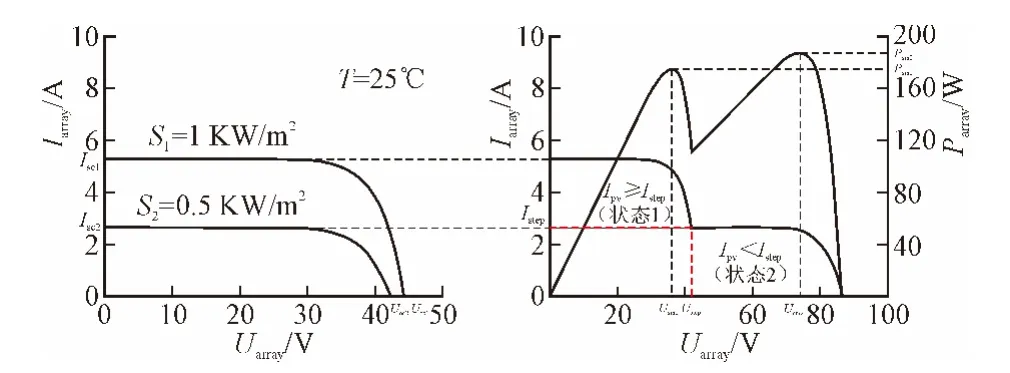
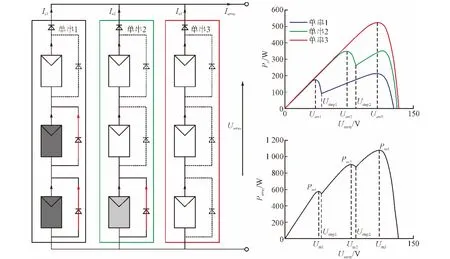
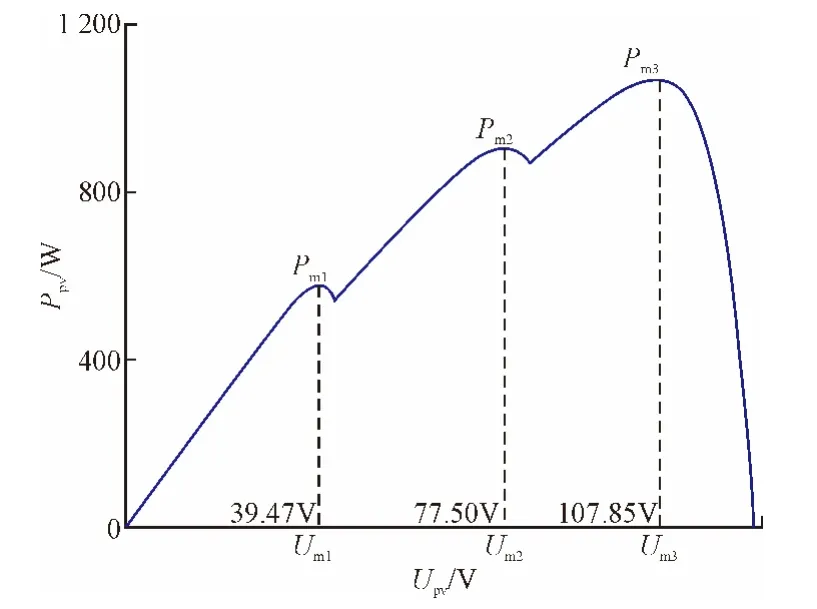
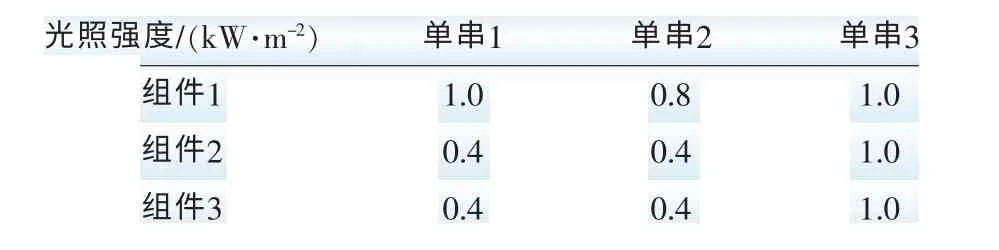
首先考虑m=2、n=1时的情形:阵列/单串由组件1和组件2串联获得(图3),组件1光照正常,光照强度为S1;组件2被阴影遮挡,光照强度记为S2。忽略温度差异,光照强度满足S2 图2 带有旁路、阻塞二极管的光伏阵列Fig. 2 PV arrays with bypass diodes and blocking diodes 图3 局部阴影条件下旁路二极管工作状态Fig. 3 Operation state of bypass diode under PSC 图4 局部阴影条件下2×1型阵列I-U、P-U特性Fig. 4 I-U characteristic and P-U characteristic of 2×1 array under PSC 当光伏阵列输出电压很小时,组件1、2都工作在恒流源区域。由于Isc2 m=2、n=1情形下,光伏阵列I-U特性满足: 当Isc2≤Iarray≤Isc1时, 由式(12),I-U分段特性的跳变点满足: 跳变电压记作Ustep满足 式(12)满足的条件等效为0≤Uarray≤Ustep 当0≤Iarray 式(12)—式(15)中的上标为组件编号。图4右图是S1=1 kW/m2、S2=0.5 kW/m2、T=25 ℃条件下光伏阵列I-U和P-U输出特性:当Uarray≤Ustep,阴影组件的旁路二极管导通,阵列/单串工作于状态1;当Uarray>Ustep,阴影组件的旁路二极管关断,工作于状态2。由于旁路二极管的存在,使得阵列输出电流为分段函数,输出功率具有多峰值特性(图4中Psm1和Psm2)。 再考虑m=3、n=3的情形:阵列由单串1、2、3并联获得,各单串由3个光伏组件串联组成,如图5左图所示。忽略温度差异,各组件光照强度信息参见表2。单串1和单串2由于存在阴影组件,旁路二极管工作,单串的P-U输出特性存在双峰;单串3中各组件光照强度一致,P-U输出曲线只有唯一的最大功率点。图5右图是各单串的P-U输出特性和阵列的P-U输出特性:由于单串1、2存在双峰,阵列的P-U特性曲线上存在3个峰值,Pm1、Pm2和Pm3,对应的输出电压分别为Um1、Um2和Um3。 m=3、n=3情形下,阵列输出电流Iarray和电压Uarray满足: 不失一般性,当m、n取任意常数时,记j、i分别是单串编号和组件编号,s和array分别为单串和阵列下(上)标。单串中各组件输出特性由式(18)—式(20)获得: 图5 局部阴影条件下3×3型阵列的单串和阵列P-U特性Fig. 5 P-U characteristics of strings and array of 3×3 array under PSC 表2 阵列光照强度(Ⅰ)Tab. 2 Solar irradiation of PV array(Ⅰ) 式中,Ui,j、Ii,j分别是单串j中组件i输出电压、电流;、、、是组件的特性参数。 当考虑阴影组件的影响,且忽略旁路二极管的导通压降前提下,Ui,j、Ii,j还应满足式(21)和式(22): 式中,Usi、Isi分别是单串i的串电压和串电流,单串i的串电流满足: 光伏阵列输出电流Iarray和电压Uarray满足: 结合式(18)—式(25),可以对局部阴影条件下光伏阵列完整建模,并描绘出阵列I-U和P-U输出特性。 文献[7]的图2(b)(c)中,将阵列的峰值电压和单串的峰值电压均标注为Vi,为了验证阵列的峰值电压和单串的峰值电压间的关系,首先以表2的模型为例,进行分析,当0≤Uarray≤Ustep1时: 输出功率P在单串峰值电压Usm1附近单调递增,因此在此条件下单串峰值电压不等于阵列的峰值电压,从而文献[7]的图2(b)(c)的标注有待商榷。 本文提出一种简单的阴影峰值电压估算方法以m×n型的阵列为例,阵列中各组件的光强级别如表3所示。 表3 光伏阵列中各组件光强级别分布Tab. 3 Solar irradiation distribution of PV arrays 表3的说明: 1)光强级别Lk指单串中光照强度第k强的级别,不同单串之间Lk级的光照强度未必相等。 2)单串n中光强级别为Lk的组件数目为Bn,k。 阴影条件下阵列多峰值电压估算步骤: 1)比较各单串中光强级别为L1的组件数目,将其中最小值记为Bmin,1; 2)第一个峰值处满足0≤Uarray≤Ustep1,单串i的功率变化率表示为(上标(i,L1)是单串i中光强级别为L1组件的简写): 当Bi,1>Bmin,1时,式(33)简化为其余情况: 需要注意的是,当跳变电流高于组件的最大功率点电流(Istep1>Im)或其他一些特殊情况,阴影条件下也可能不存在峰值点。 以表2所示的阵列光照强度情况为例: 当0≤Uarray≤Ustep1 由0≤Uarray≤Ustep1 当Ustep1≤Uarray≤Ustep2,此时满足: 图6 光照强度(Ⅰ)时多峰值仿真结果Fig. 6 Simulation result of multi-peak voltage under solar irradiation(Ⅰ) 在表5所示情形下,共有两个峰值,求解第一个峰值电压: 表4 光照强度(Ⅰ)时估算值与仿真值比较Tab. 4 Comparison between the estimated peak voltage and the simulation value under solar irradiation(Ⅰ) 表5 阵列光照强度(Ⅱ)Tab. 5 Solar irradiation of PV array(Ⅱ) 当0≤Uarray≤Ustep1 代入上式化简:解得Uarray=36.75 V,与仿真值36.75 V一致。 本文从文献[14]的工程方法入手,对局部阴影条件下光伏阵列建模方法进行了详细的推导。在此基础上提出了一种基于光伏阵列模型的局部阴影条件下多峰值电压估算方法,得到如下结论: 1)阵列的峰值电压和单串的峰值电压之间不存在等同关系。当不考虑温度变化时,阵列的峰值电压只取决于各组件光照强度以及相同光强级别组件的分布; 2)采用本文所提出的方法,可以估算出前k-1个峰值电压。与仿真结果相比,估算精度可达到0.1 V。验证了估算方法的可行性和优越性。 对局部阴影条件下多峰值电压估算简化了局部阴影条件下复杂的光伏模型,为多峰值MPPT算法和验证提供了新的思路。 [1] 赵争鸣,刘建政,孙晓瑛. 太阳能光伏发电及其应用[M].北京:科学出版社,2008. [2] 许洪华.中国光伏发电技术发展研究[J].电网技术,2007,31(20):77-81.XU Honghua. The study on development of PV technology in China[J]. Power System Technology,2007,31(20):77-81(in Chinese). [3] MUTOH N,OHNO M,INOUE T. A method for MPPT control while searching for parameters corresponding to weather conditions for PV generation systems[J]. IEEE Transactions on Industrial Electronics,2006,53(4):1055-1065. [4] QI Jun,ZHANG Youbing,CHEN Yi. Modeling and maximum power point tracking(MPPT)method for PV array under partial shade conditions[J]. Renewable Energy,2014(66):337-345. [5] 肖景良,徐政,林崇,等. 局部阴影条件下光伏阵列的优化设计[J]. 中国电机工程学报,2009,29(11):119-124.XIAO Jingliang,XU Zheng,LIN Chong,et al. Optimal design of photovoltaic arrays under partial shading[J].Proceedings of the CSEE,2009,29(11):119-124(in Chinese). [6] 卞海红,徐青山,高山,等. 考虑随机阴影影响的光伏阵列失配运行特性[J]. 电工技术学报,2010,25(6): 104-109.BIAN Haihong,XU Qingshan,GAO Shan,et al. Operation mismatches of photovoltaic array considering random shadows[J]. Transactions of China Electrotechnical Society,2010,25(6):104-109(in Chinese). [7] 刘东冉,陈树勇. 光伏发电系统模型综述[J]. 电网技术,2011,35(8):47-52.LIU Dongran,CHEN Shuyong. A review on models for photovoltaic generation system[J]. Power System Technology,2011,35(8):47-52(in Chinese). [8] ISHAQUE K,SALAM Z. A deterministic particle swarm optimization maximum power point tracker for photovoltaic system under partial shading condition[J]. IEEE Transactions on Industrial Electronics,2013,60(8):3195-3206. [9] JI Y,JUNG D,KIM J,et al. A real maximum power point tracking method for mismatching compensation in PV array under partially shaded conditions[J]. IEEE Transactions on Power Electronics,2011,26(4):1001-1009. [10] ISHAQUE K,SALAM Z,AMJAD M,et al. An improved particle swarm optimization(PSO)-based MPPT for PV with reduced steady-state oscillation[J]. IEEE Transactions on Power Electronics,2012,27(8):3627-3683. [11] PATEL H,AGARWAL V. Maximum power point tracking scheme for PV systems operating under partially shaded conditions[J]. IEEE Transactions on Industrial Electronics,2008,55(4): 1689-1698. [12] N ALAJMI B,H AHMED K J. FINNEY S,et al. A Maximum power point tracking technique for partially shaded photovoltaic systems in microgrids[J]. IEEE Transactions on Industrial Electronics,2013,60(4):1596-1606. [13] 孙博,梅军,郑建勇. 局部阴影条件下最大功率点跟踪改进算法[J]. 电力自动化设备,2014,34(1):115-119.SUN Bo,MEI Jun,ZHENG Jianyong. Improved MPPT method under partial shading conditions[J]. Electric Power Automation Equipment, 2014, 34(1): 115-119 (in Chinese). [14] 戚军,翁国庆,章旌红. 光伏阵列多峰最大功率点分布特点研究[J]. 电力自动化设备,2014,34(3):132-137.QI Jun,WENG Guoqing,ZHANG Jinghong. Multi-peak MPP distribution of photovoltaic array[J]. Electric Power Automation Equipment, 2014, 34(3): 132-137 (in Chinese). [15] 茆美琴,余世杰,苏建徽. 带有MPPT功能的光伏阵列Matlab通用仿真模型[J]. 系统仿真学报,2005,17(5):1248-1251.MAO Meiqin,YU Shijie,SU Jianhui. Versatile matlab simulation model for photovoltaic array with MPPT function[J]. Journal of System Simulation,2005,17(5):1248-1251(in Chinese). [16] SCARPA V,BUSO S,SPIAZZI G. Low-complexity MPPT technique exploiting the PV module MPP locus characterization[J]. IEEE Transactions on Industrial Electronics,2009,56(5): 1531-1538. [17] 杨永恒,周克亮. 光伏电池建模及MPPT 控制策略[J]. 电工技术学报,2011,26(1):229-234.YANG Yongheng,ZHOU Keliang. Photovoltaic cell modeling and MPPT control strategies[J]. Transactions of China Electrotechnical Society,2011,26(1):229-234 (in Chinese).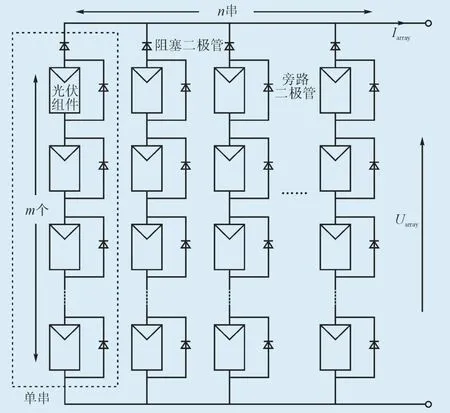
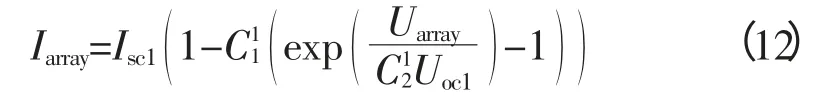
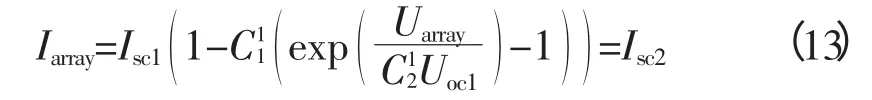
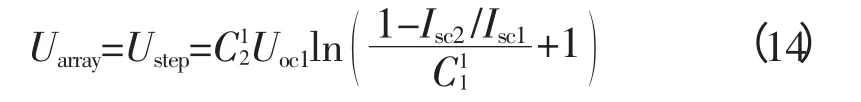
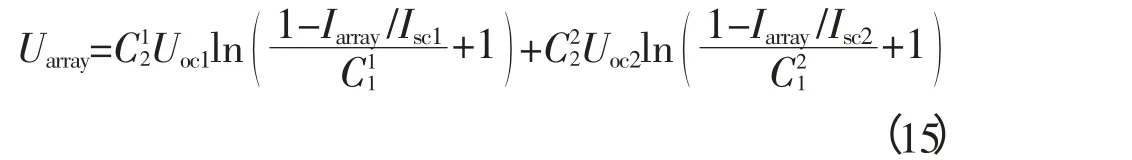
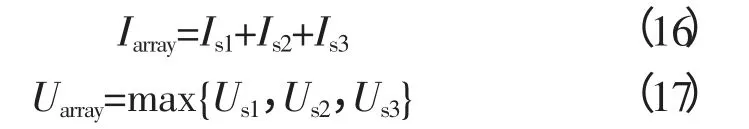

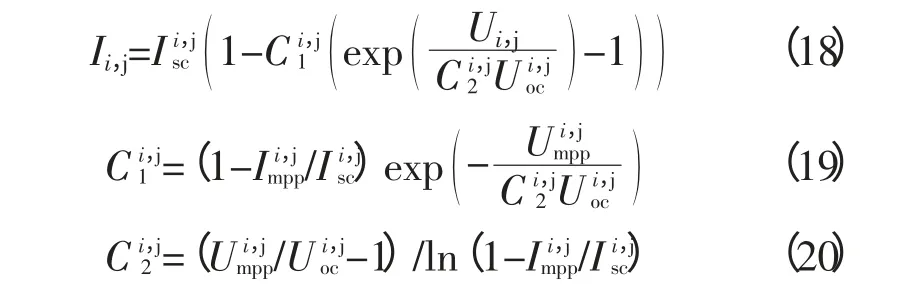



3 阴影条件下阵列多峰值电压估算
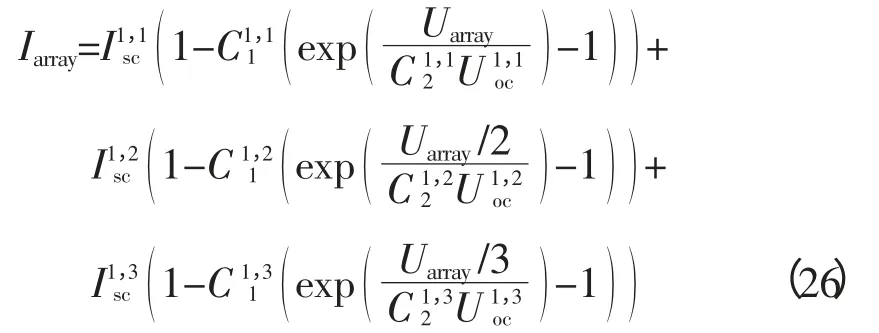
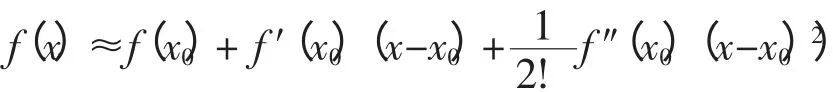
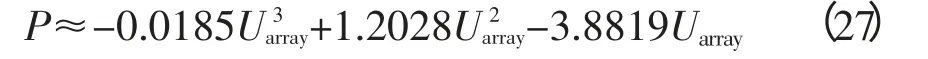

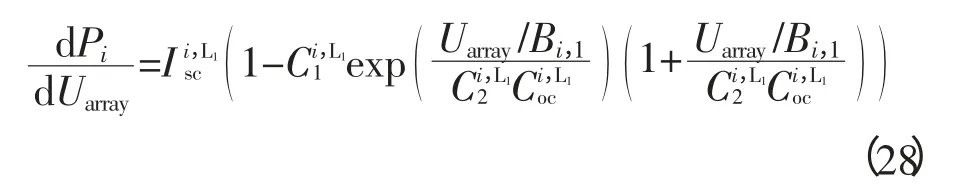
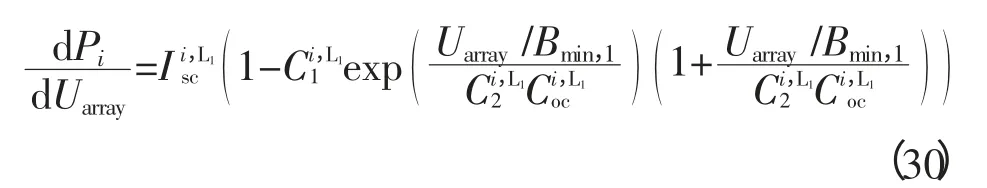

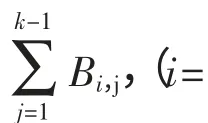

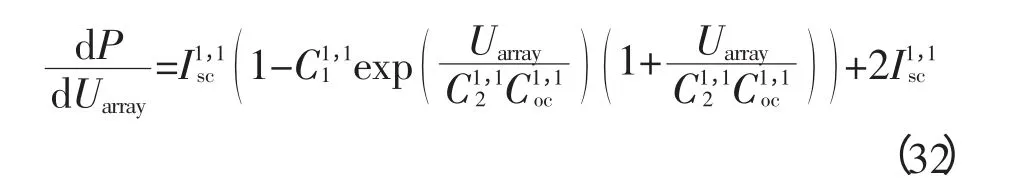
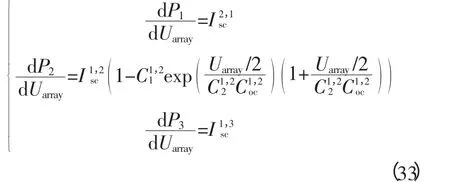

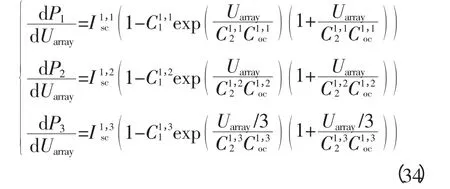
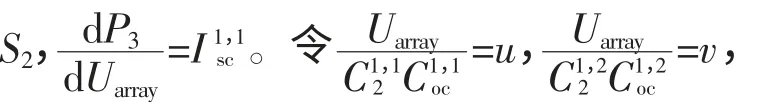
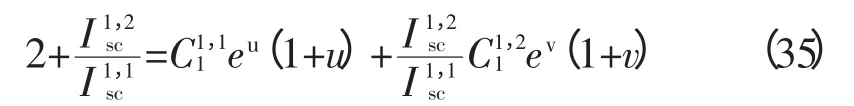
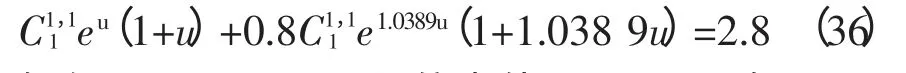
4 结论

