S型曲线加减速方法的研究

冯瑞珏

（华南理工大学 广州学院，广东 广州 510800）

在数控机床加工中， 为了提高数控系统的加工精度以及加工效率，需要对机床各运动轴的输出进行加减速处理，因此机床加减速控制是计算机数字控制系统的重要组成部分[3]。 传统的CNC 加减速方法主要有直线加减速、 指数加减速以及S 曲线加减速方法。使用直线加减速和指数加减速方法时，速度的变化相应较快，但由于存在加速度突变从而产生冲击，因此不适用于高速数控系统；而对于传统普通的S 曲线加减速方法，其通过对加速阶段以及减速阶段进行平滑处理来减少机床的冲击， 然而其加减速阶段存在突变以及加加速度并不连续， 从而使机床柔性受到限制。

为此，考虑到以上各种加减速方法的不足，本文对传统S 型曲线加减速方法进行改进。 利用三角函数对加减速曲线的加减速段曲线进行构造，得到另一种加减速模式，实现加减速段的平滑过渡以及加加速段的连续。

1 基于三角函数构造加减速阶段的S 型曲线加减速方法

图1 所示为基于三角函数构造加减速阶段的S 型曲线加减速方法（以下简称S 型曲线加减速法）全过程的位置、速度、加速度以及加加速度曲线图。 一共分为7 个阶段：加加速段（区域a表示）、匀加速段（区域b 表示）、减加速段（区域c 表示）、匀速段（区域d 表示）、加减速段（区域e 表示）、匀减速段（区域f 表示）、减减速段（区域g 表示）。 在图中，ti（i=1，2…7）为各个区域的过渡时间点；Vs 为起始速度，Ve 为终点速度，Vmax 为给定最大速度；Amax 为给定最大加速度绝对值。 由于S 型曲线加减速法的加速段和减速段相似， 因此接下来只分别对S 型曲线加减速法的加速阶段和匀速阶段进行讨论。

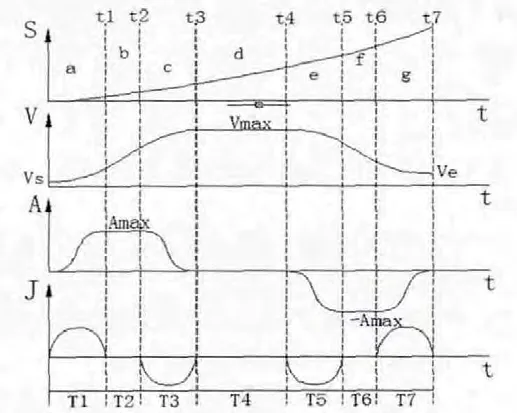
图1 S 型曲线加减速法过程图

1.1 加速阶段

如图1 所示，S 型曲线加减速法的加速阶段由区域a、b 和c组成。 以加速度曲线为研究对象，假设加速阶段的实际加速度为Aac1，利用三角函数cos 为基础对区域a 进行曲线构造，结合待定系数法可得以下方程组：

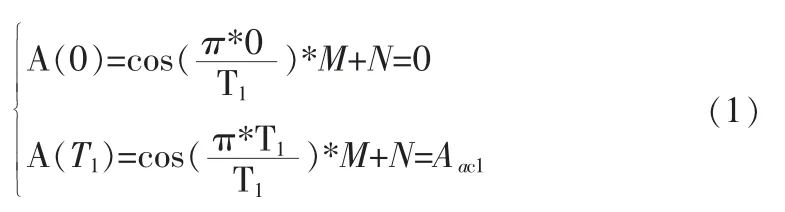
解得：

由此可得区域a 加速度曲线函数为：

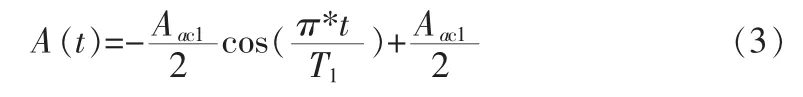
同理可得区域c 的加速度曲线函数为：

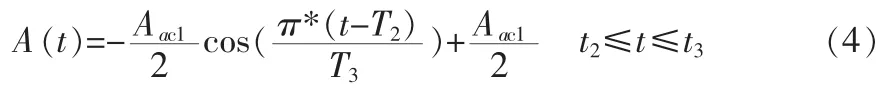
而对于区域b，由于此区域属于横加速段，其加速度保持为Aac1，由此得出区域b 的加速度曲线函数为：

利用公式（3）、（4）、（5）根据加速度对时间t 的微分关系，以及加速度、速度对时间t 的积分关系，可导出相应的加加速度J（t）、速度V（t）和位移S（t）计算公式如下：

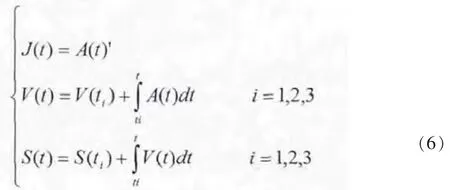
1.2 匀速阶段

如图1 所示，区域d 为S 型曲线加减速法的匀速阶段，由于此时该区域的速度保持为Vmax， 由此可得区域d 的加加速度J（t）、加速度A（t）、速度V（t）和位移S（t）计算公式如下：

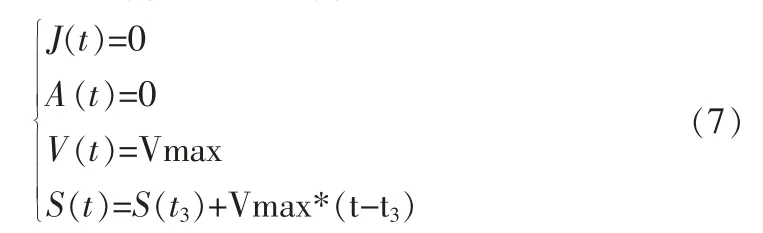
2 基于三角函数构造加减速阶段的S 型曲线加减速方法的讨论

如图1 所示，ti（i=1，2，……7）表示S 型曲线加减速各个阶段的时间点，Ti（i=1，2，……7）表示各个阶段的运行时间。 一般情况下，S 型曲线加减速的加速阶段和减速阶段的加速度大小值将会被设为相同， 设Tac为加速阶段运行时间，Tde为减速阶段运行时间，根据图1 可得出：

Tac和Tde的计算将和直线加速度方法一样，即有：

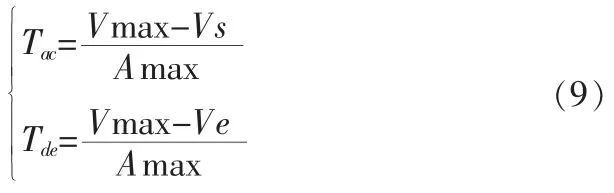
根据加速度曲线的对称性，有：

对于加加速段（区域a 表示），由公式（3）可得出区域a 的加加速度曲线函数：J

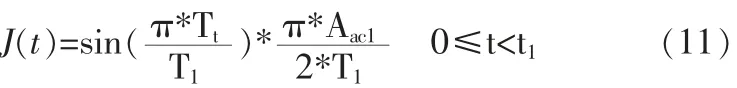
由此可算出：

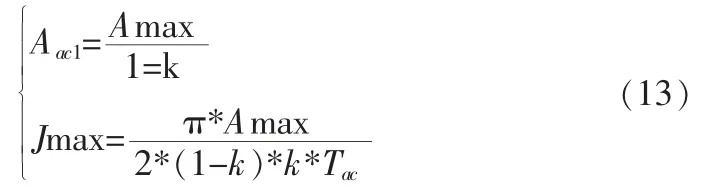
因此，区域a 的最大加加速度Jmax 可根据k 的相应设定来确定。 这样， 当系统的最大给定速度Vmax、 最大给定加速度Amax 以及设定时间比例系数k 设定后，再根据具体代码的长度S、起始速度Vs 以及终止速度Ve 可确定整个S 型曲线加减速运动过程。其中最大加速度反映了系统的最大运动能力，最大加速度放映了系统的最大加减速能力， 时间系数k 确定了系统的加加速度， 从而保证了系统的柔性。 当时间系数k 设定为0 时，S型曲线加减速则退化为直线型加减速。 在实际运用中，可以根据实际需要对时间系数k 进行设定。

3 总结

本文对传统的S 型曲线加减速法进行了改进， 对基于三角函数构造加减速阶段的S 型曲线加减速方法进行了研究。 该方法计算得出的加减速曲线实现了平滑过渡， 速度曲线和位移曲线也保持了平滑的效果， 较好地解决了传统S 型曲线加减法在加减速阶段存在突变以及加加速度并不连续的问题， 从而使得数控系统的柔性得到进一步的提高， 是一种适用于高速切削的柔性加减速方法。

[1]郭新贵，李从心.S 曲线加减速算法研究[J].机床与液压，2002（5）:60-62.

[2]张碧掏，高伟强，沈列，等.S 曲线加减速控制新算法的研究[J].机床与液压，2009，37（10）:27-29.

[3]徐川，王永章，刘源.多项式加减速控制方法研究[J].组合机床与自动化加工技术，2009（9）:42-44.

[4]郭永忠.三角函数在数控机床中的应用[J].中国科教创新导刊，2009，（25）:170-170.

[5]冷洪滨，邬义杰，潘晓弘.三次多项式微型高速加工速度规划算法研究[J].计算机集成制造系统，2008（2）:336-340.