例谈平移思想在初中几何中的运用

施纯长

[内容摘要]平移是初中数学几何变换的常用方法之一，它是图形的一种变换，在这种变换中图形的形状和大小都不改变（不变性），只是改变了图形的位置（改变性）。利用平移的不变性和改变性，对解决零散图形的求值问题特别有效，利用平移的思想可以把复杂的问题简单化，这是一种重要的数学思想，在几何问题中有着广泛应用，同样也是中考的热点。

[关键词]初中数学;平移;运用;证明

平移是将几何图形中的各顶点沿它们所在的一组平行线向同一方向移动相同的距离，这种几何变换的方法叫平移变换。平移变换有如下性质：平移后的图形与原来图形连结对应点的线段平行（或在同一条直线上）且相等;对应线段平行（或在同一条直线上）且相等;对应角相等;图形的形状与大小都没有发生变化。平移变换只改变图形的位置，而不改变图形的大小和特征，但是它可以将线段和角平移到一个新的位置，从而把比较分散的已知条件集中到一起，使问题得以解决。平移包括以下三个方面的应用：第一，集中分散的条件;第二，将复杂图形变得简单明了;第三，转换题目的形式。下面笔者通过具体的例题来说明平移思想在初中数学中的运用。

一、平移在三角形相关题目运算和证明中的运用

1.利用平移证明角之间的关系

例：已知三角形ABC，利用平移说明∠A+∠B+∠C=180°。

分析：如图，将AB平移到CD，并将BC延长，得到∠B=∠DCE，∠A=∠ACD，即∠A+∠B+∠C=∠ACD+∠DCE+∠ACB=180°。

2.利用平移求三角形边长

例：如图为某楼梯，测得楼梯的长为5米，高3米，计划在楼梯的表面铺地毯，地毯的长度至少需要多少米？

分析：由勾股定理可知AC= =4m，将楼梯平行于BC的边都平移到BC上，平行于AC的边都平移到AC上，因此地毯的长度等于AC+BC=7米。

二、平移在梯形相关题目运算和证明中的运用

初中阶段在学习与梯形有关的几何证明和运算中，平移思想的运用几乎涵盖了大半题型，因此这也成为我们在讲授与梯形有关内容时必须重视的地方。

1.平移一腰或两腰

平移一腰或两腰时，注意把握以下要领：平移一腰，使之经过梯形的另一个顶点或另一条腰的中点;或者同时移动两腰使它们交于一点。

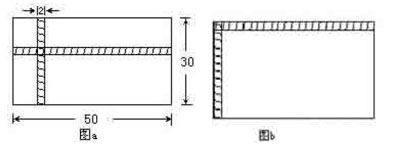
例：如图，在梯形ABCD中，AD∥BC，AD

分析：过点E分别作EH∥AB、EG∥CD，分别交BC于H、G。

由于EH∥AB、AD∥BC，从而四边形ABHE是平行四边形，同理可得四边形CDEG是平行四边形，再利用线段垂直平分线的性质得到EH=EG，推导得出四边形ABCD是等腰梯形，故∠B=∠C。

题目需要证明的几条线段是分散的，通过平移变换可以将AB、EF、DC集中到一起。此时，各个条件都能很好地得以应用。

2.平移对角线

平移一条对角线，使之经过梯形的另一个顶点，构造平行四边形，利用有关平行线的性质解决问题。

三、利用平移求面积

由于图形的平移不改变图形的形状和大小，因此在求一些图形的面积时，利用图形的平移可以巧妙地将这些原本很难直接解决的数学问题变得简单。

例：如图a，在一个长方形的草坪上有两条等宽且互相垂直的长方形小路（长度单位：m），那么草坪的面积为         m2。

分析：将两条小路分别作如图b所示的平移，则草坪的面积就是空白部分（长方形）的面积，即（50-2）×（30-2），为1344m2。如果用传统方法求面积，计算过程相对繁琐，学生容易把中间的重叠部分重复计算，从而使计算产生错误，利用平移方法求几何图形的面积，使图形又变成一个矩形，计算十分方便、准确。

总之，平移可以将一些复杂的问题通过简单的平移转换题目的形式，使题目由复杂变简单，使题目得以解决。一些看似棘手的问题常常可以通过平移及平移的性质获得巧解，对于某些几何计算题，在不改变面积的前提下，采用平移的方法适当改变图形的形状或位置，可以更好地解决问题。我会在今后的教学中更加重视平移思想的渗透，让学生更多地了解平移的使用价值。

（责任编辑 冯 璐）