基于FPGA的三相电网故障环境下锁相技术分析
刘 超,庄圣贤,刘思佳,谢茂军
(1.西南交通大学信息科学与技术学院,四川成都 610031;2.西南交通大学电气学院,四川成都 610031)
在光伏并网逆变器设备中准确实时地追踪电网频率和相位是并网不可缺少的环节。文献[1]中全面综述了过零点检测、锁相环、加权最小均方差估计和变换角检测等常用的相位追踪方法。本文采用目前应用较为普遍的相位同步方法,即基于同步旋转坐标变换的三相锁相环。文献[2~3]说明此方法下的三相锁相环适用范围广、鲁棒性强。文献[4~6]中分析了电压不平衡、直流分量和谐波等干扰下采用DSP技术以软件方式实现数字锁相环。在DSP平台下实现PLL优点是比较灵活,但是对CPU资源耗费大导致性能受限。本文采用全新的流水线结构编写Verilog HDL语言在FPGA里实现三相锁相环的4个模块,即dq变换鉴相器、PI环路滤波器、数控振荡器和cordic算法模块。各模块以纯硬件电路并行运行,不占CPU资源,且由于采用流水线结构,其中cordic模块和乘法器等资源可以分时复用大幅节约了资源。在各模块内部流水线准确地时序控制便可以高效的实现三相锁相环。最后本文通过 Matlab模拟各种电网故障,并通过Modelsim仿真验证。仿真结果表明,该系统的动态响应速度快,抗干扰能力强。
1 三相锁相环基本框架和工作原理
由图1得到三相PLL在的结构和工作原理。由于坐标变换算法的优越性,基于坐标变换的三相锁相环研究比较多。文献[2,4~7]均对此方法进行了介绍。锁相环主要由鉴相器(PD)、环路滤波器(LF)和压控振荡器(VCO)组成,本文以旋转坐标变换作为系统鉴相器。将三相采样电压ua、ub、uc通过clark变换从三相静止abc坐标系到两相静止αβ系,再以d轴定向从两相静止αβ坐标系到同步旋转坐标dq系[8]。输出的ud就是锁相环输出估计角θ*和输入相角θ的差值,该相位差信号经过PI调节锁定到输入信号的角频率ω,最后通过数控振荡器对ω积分即可得到锁相环输出跟踪相位。通过PLL对三相电网相位的准确的追踪,为实现并网电流对电网的同步运行,即相位相同、频率相同,提供了重要的前提。

图1 三相锁相环原理图
1.1 dq坐标变换鉴相器
传统过零鉴相器虽然实现简单,但面对电网中的谐波、毛刺等情况会存在多个过零点,以致锁相失败[9]。为解决这一问题,本文采用dq同步坐标轴变换实现锁相环鉴相器功能。
通过ADC采样的三相电网电压数字信号经归一化后表示为

式(1)中 ua、ub、uc是瞬时电网电压;θ是 a相瞬时相位角。
uα=U sinθ,uβ=U cosθ通过静止坐标变换,三相电压矢量投影到两相静止坐标系上有

式(2)中Tαβ为静止坐标变换矩阵

通过同步坐标变换uα、uβ投影到同步旋转坐标系下

式(3)中Tdq是同步坐标变换矩阵

求出d轴分量为

三相锁相环原理即通过PI控制器调节ud~0,从而实现相位频率锁定。对电网电压信号的相位频率锁定后θ和θ*趋于相等,即两者之差趋于零,可以线性化式(4)为

从式(4)~式(5)中可看出,dq坐标变换输出ud即为电网电压相位角与锁相环输出的估计角,完成了两者相位差的计算。
最后输出并网三相电流为

其中
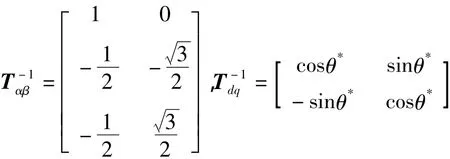
1.2 使用cordic算法计算三角函数
采用硬件电路对锁相环的各个算法模块进行实现,其中涉及到的乘法运算会耗费大量的资源,同时由于三角函数的实现通常采用查表法,该方法会占用大量的片内RAM资源,并且精度越高,资源耗费越大。本文为了适应FPGA的特点,采用Cordic(Coordinated Rotation Digital Computer)算法计算三角 函数[10]。Cordic算法只需用到移位以及加减法等简单运算,因而在硬件电路上能够高效而简便地实现。
1.3 PI环路滤波和NCO数控振荡器
本文采用具有良好控制性能的PI控制器作为本次设计的环路滤波器。其传输函数为

其中,Kp为控制器的比例系数;Ki为控制器的积分系数。输入偏差与输出频率控制信号的关系为
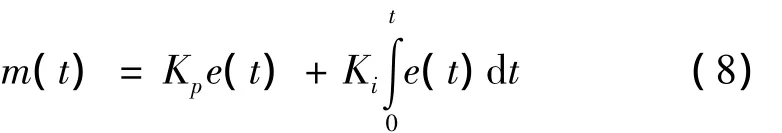
离散化数学模型为

m(n)即为本文实验所要观察的频率控制字信号。
通过文献[6]分析要考虑动态响应能力,Ki越大响应就越快,但环路的稳定性和滤波效果越差,因此速度与稳定性和滤波效果之间存在矛盾[11]。所以本文采用比例积分控制器。
最后本文通过数控振荡器对环路滤波器输出的频率控制字进行累加,为避免溢出,累加到2π时清零,重新开始累加,以达到跟踪输入正弦波角频率的目的。数控振荡器环节的表达式为

2 三相锁相环在FPGA中实现结构及优化
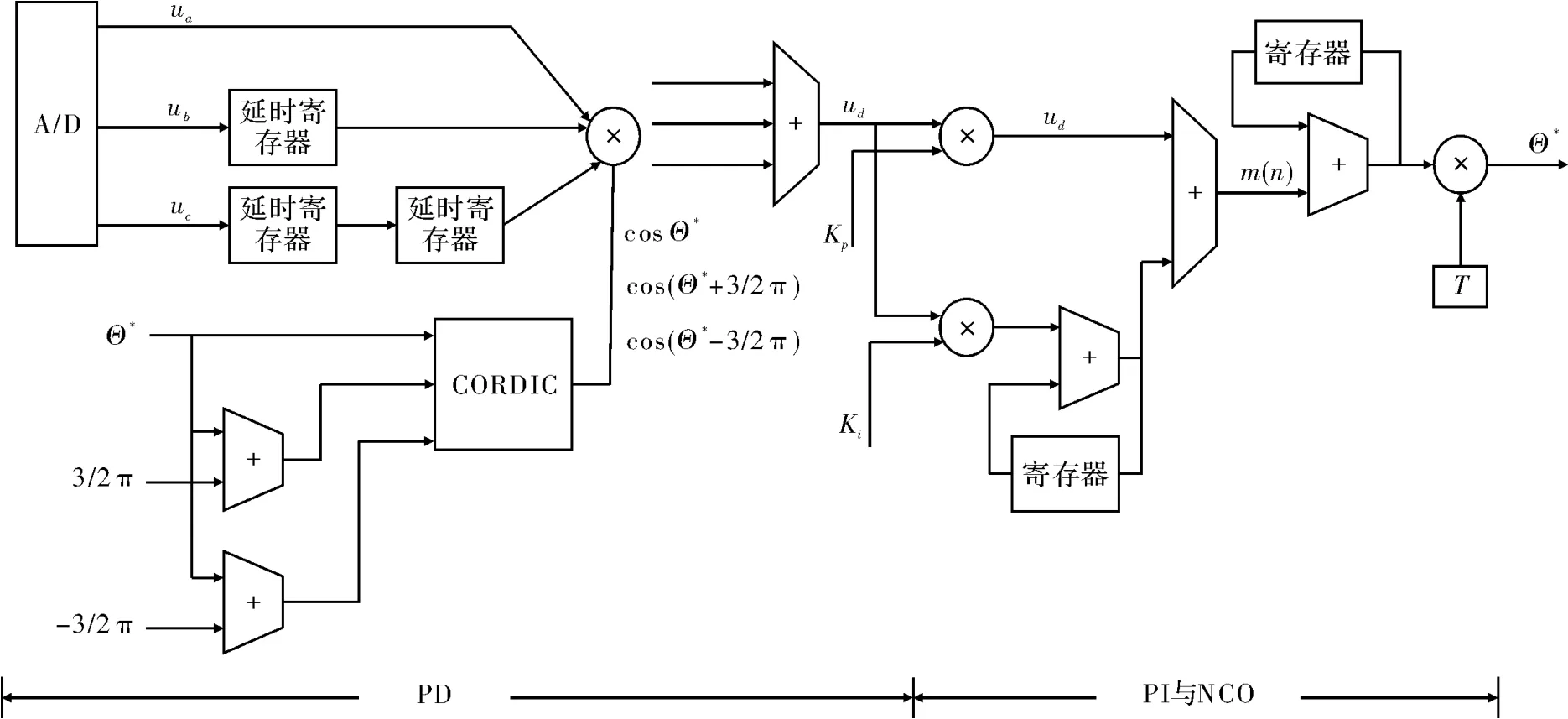
图2 三相锁相环在FPGA中的硬件设计框图
2.1 鉴相器数字化
由图1和式(3)可知,三相锁相环只需利用dq坐标转换的ud分量
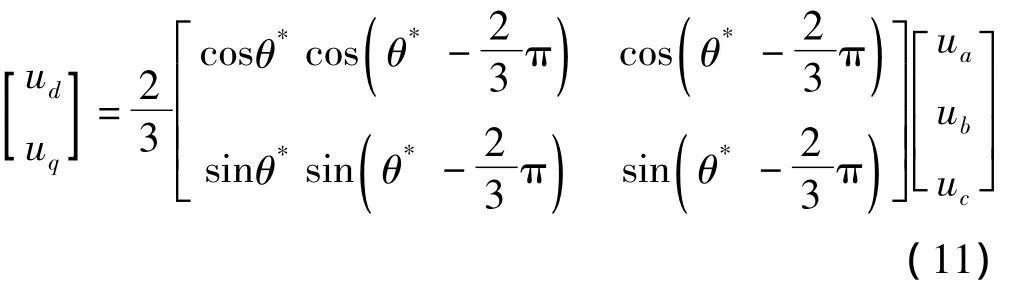
有

从式(12)可看出,完成该运算需要,4次乘法4次加法两次调用cordic三角函数模块。若进行以下变换

从图2和式(13)可得,由于文中cordic算法使用16级流水线结构,所以把上式中的3次cos并行调用cordic块,每调用一次分别延时一个时钟。由于复用cordic块,可节约两个cordic块资源。ub和uc分别延时一个和两个时钟后与cordic输出对齐,再分别进行相乘,乘法器也只用一个。但是由2个时钟延时最后得到ud,从实现数据看,对结果没有影响。
2.2 环路滤波器和压控振荡器
由图2和式(9)得到环路滤波器的离散数学模型可看出,该环节的实现需要两个乘法器和两个加法器。其中,PI参数Kp、Ki决定了系统控制性能在经过折中处理后取 Kp=0.022,Ki=0.003,系统采样频率为10 kHz。
由于鉴相器的输入范围是0~2π,所以数控振荡器的离散数学模型改为
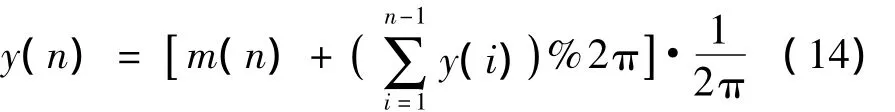
如式(14)所示,数控振荡器数学模型中包含两个加法器和一个乘法器。通过对累加角度求模,实现角度的归一化。
3 电网故障及Modelsim仿真结果分析
本文仿真结果均通过频率控制字观察。仿真系统中,设定三相电网电压的采样频率Fs=10 kHz,电网工频Fc=50 Hz,对采样频率归一化后的数字角频率ωs=2π≈0.031 4。在电网电压正常运行下,锁相环输
出频率控制字基本上稳定在0.031 4。
3.1 三相不平衡分析
电网电压出现不平衡时,可表示为

式(15)中β和τ是电网bc两相不平衡分量系数。通过clark变换有

从上式可看出,三相电压经过两相静止坐标变换后存在不平衡分量。再将上式通过dq变换则有

其中
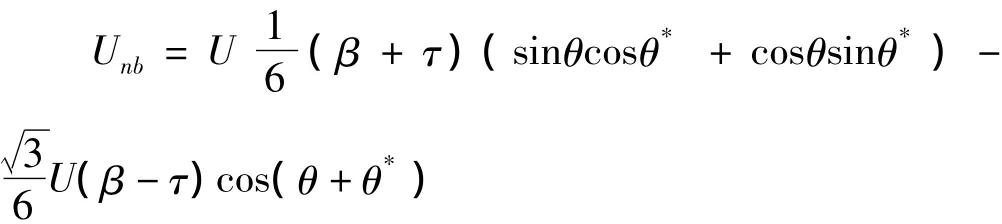
由于相位锁定后,θ约等于θ*,所以上式可以简化为

如式(18)所示,在不平衡电网环境下会鉴相器输出会出现基波的2倍频分量。
图3为Modelsim三相不平衡时仿真结果(β=-0.3,τ= -0.5)。

图3 三相不平衡的仿真图
如图3所示,lf_out输出有一定抖动,频率控制字为lf_out/226,最大为0.034 3,最小为0.029 47。误差0.000 3 rad,因此系统满足设计要求。
3.2 高次谐波影响
三相电网含有奇数次谐波时

式(19)中n代表所含谐波次数,本文对含有3、5、7次谐波的电网进行计算并且仿真。两相静止坐标变换有
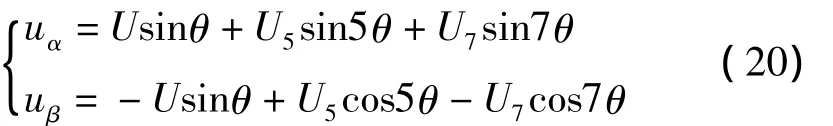
通过dq变换后有

从上式中可看出,在相位锁定后会相位差值信号出现偶数次谐波。同理若在电网中存在偶数次谐波,则输出会包含奇次谐波。
图4所示,稳态输出有波动,据分析在一个周期内频率控制字lf_out最小值为0.026 96,最大值为0.035 113 6。波动范围0.003 7~0.004 4 rad。虽然在鉴相器输出中会含有一定量的谐波干扰,在经过系统环路滤波器后干扰得以减小,最终在锁相环输出的追踪相位角中基本不含谐波,满足设计要求。
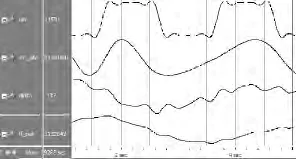
图4 含有3、5、7次谐波三相锁相环仿真图
3.3 直流分量影响

式(22)中 UDCa、UDCb和 UDCc分别代表 abc三相电压中所含的直流分量。经过两相静止坐标变换后有


从式(24)看出锁定后,输出含有与输入同频率的信号干扰。
本次仿真中abc三相分别加入10%、20%和30%的直流分量,从图5可看出频率控制字的输出范围在0.027 9~0.035 5 rad,在理论范围之内,与式(24)分析一致。

图5 直流分量影响时鉴相器和频率控制字输出
3.4 在不同环境下的分析
abc三相电压输入不平衡、含有直流分量及大量的高次谐波。
对应具体输入量,在输出稳定后,本系统相位控制字输出最大值0.036 4,最小值为0.026 9,平均值为0.031 65。可见在有综合电网故障环境下,此算法的锁相环输出仍能有效地跟踪电网基波相位。

图6 谐波、直流分量且三相不平衡时锁相环输出
3.5 频率突变时仿真
在输入三相对称无谐波的电压信号时,中间某时刻电网频率从50 Hz突然跳变到55 Hz幅值不变。此时,相应的仿真为图7所示,该算法可较好地克服电网频率突变,在一定时间后能正确地追踪电网基波相位。

图7 在1 s时发生发生频率突变锁相环输出
3.6 相位突变时仿真
当三相对称电压输入相位在1 s时发生突变,得到的输入、输出相位如图8所示,此算法在相位发生突变的情况下还能较好地调节和追踪变化后的基波相角。
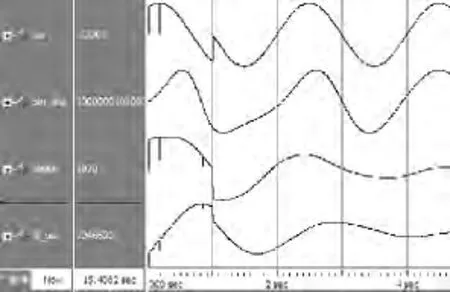
图8 相位突变时锁相环输出
4 结束语
本文通过流水线和模块化的理念,利用Verilog语言解决了三相锁相环在FPGA平台上的实现。由于流水线对资源的复用,所以节省了FPGA上的资源。
从实验结果可看出,在极为恶劣的环境下,包含电网电压大幅度不平衡、直流分量严重、含大量谐波、频率突变和相位突变等情况,本文所设计的系统均能良好地实现对电网电压基波相位锁定,说明该系统具有较好的抗干扰能力。因此,该系统适用于并网光伏逆变器和工作环境恶劣的电力电子装置中。
[1]胡为兵,李开成.电力系统实时相位同步方法的研究和比较[J].电测与仪表,2007,44(8):1-4.
[2]舒泽亮,郭育华,汤坚.基于 FPGA的三相锁相环实现[J].电力电子技术,2005,39(6):126 -128.
[3]BANISLAV D,EDDY S.Phase measurement of distorted periodic signals based on nonsynchronous digital filtering[J].IEEE Transactions on Instrum,Meas,2001,50(4):864 -867.
[4]Se Kyo Chung.A phase tracking system for three phase utility interface inverters [C].IEEE Transactions on Power Electronics'00,2000:431 -438.
[5]龚锦霞,解大,张延迟.三相数字锁相环的原理及性能[J].电工技术学报,2009,24(10):94 -99.
[6]周国梁,石新春,付超.三相电压畸变条件下软件锁相环分析与实现[J].电力电子技术,2007,41(7):47 -49.
[7]孙浩,袁慧梅.基于FPGA的三相锁相环的优化设计方案[J].电力系统保护与控制,2009,37(10):98 -110.
[8]张兴,张崇巍.PWM整流器及其控制[M].北京:机械工业出版社,2012.
[9]孔雪娟,罗畴,彭力,等.基于周期控制的逆变器全数字锁相环的实现和参数设计[J].中国电机工程学报,2007,27(1):60-64.
[10]陆鹏威,梅杓春.基于cordic算法实现三角函数的运算[J].理论与方法,2008,27(1):10 -11.
[11]FELICE L,POMPEO M,GIULIANO R.Robust and fast Three- phase PLL tracking system[J].IEEE Transactions on Industrial Electronics,2011,58(1):221 -231.

