基于贝叶斯概率的煤炭销售推荐

薄利军，夏文杰，闫新庆

(华北水利水电大学信息工程学院，河南郑州 450011)

我国是一个能源消耗大国，在众多能源消耗中，煤炭能源占绝大部分。据预测，到2020年全国煤炭消费量将达到约48亿吨。目前，煤炭在我国一次能源消费结构中的比重在60%以上，煤炭工业仍具有较大的发展空间［1］。煤炭销售关系到国家的经济发展和企业的切身利益。

在大型煤炭企业的销售中，矿井、运销公司和客户构成了星形网络，运销公司位于网络的中心。矿井通过内部结算方式将生产的煤炭销售给运销公司，运销公司再将煤炭销售给客户。由于煤炭运输的局限性，部分大型客户和煤炭企业构建了战略联盟关系。

2006年以来，我国煤炭销售采用质量分级的发热量浮动计价政策，这使得煤炭产品在交易中的价格计算有了明确的标准，规避了传统吨煤计价政策所导致的质量与价格的偏离问题，但也带来了交易双方因检测值不同产生的贸易纠纷等新问题。同时市场环境的变化使得煤炭企业逐渐从片面追求利润最大转向构建战略联盟，形成了区域煤炭市场垄断供给局面［2］。

但由于采样的随机性，矿井与客户对同一批煤采样得到的发热量值均不同，致使贸易纠纷的产生，影响交易双方的信誉。针对这一情况，本文通过对双方大量历史交易数据的深入研究，提出应用贝叶斯概率进行煤炭交易对象的选择推荐。

贝叶斯概率主要用来表示事件在条件下发生的概率，其在邮件过滤、水文预测、数据挖掘等方面均有广泛应用［3－4］。在研究中，针对大型煤炭企业销售，根据双方以往交易次数所占各自交易比例和双方无争议交易次数，较真实和准确地预测双方下次成功交易的可能性，在此基础上提出应用贝叶斯概率计算交易双方的信誉度，使得运销公司比较各种可能交易对象的信誉度，实现销售的最优选择推荐，降低了交易双方产生贸易纠纷的可能，保证交易各方的利益。

1 贝叶斯概率

贝叶斯定理由英国数学家贝叶斯提出，用来描述两个条件概率之间的关系，其基本公式为

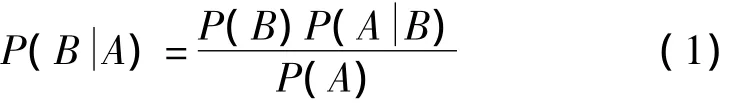
对上述公式进行变形，可得到随机事件的贝叶斯公式:若 B1，B2，B3，…，为一系列互不相容的事件，且

则对任一事件A，有

其中，i=1，2，…。

式(2)中A表示已发生的事件，引起A发生的可能性有i种(最大为无穷个，实际中可能为n个)，每种事件为Bi，P(Bi)表示先验概率，是在A发生前就发生的，通过计算可直接得到表示 Bi引起A发生的概率，称为后验概率越大，则表示Bi引起A发生的可能性越大［5］。

对于煤炭交易双方而言，由于双方交易环境相对稳定，在一段时期内产生的交易数据就有了较高分析价值。例如，对于某一矿井，其有若干客户，而每个客户所占交易比例不同，且矿井和客户进行交易时，双方的无争议成交比例也不相同，则在矿井需选择客户时，通常希望交易的对象是与其交易次数较多且无争议成交比例较高的客户。同样，客户在选择矿井时也遵循这一原则，而这两个因素均可通过概率统计表示，且每一笔交易又可看成是一个随机事件，因而可通过随机事件的贝叶斯公式来进行相关数据的统计分析。将这两部分的统计结果用一个概率表示，其可称之为信誉度值，其值范围为［0，1］，决定因素即为双方交易次数所占矿井(客户)交易总次数比例和双方无争议成交比例。可根据需要对影响因素设置不同的权值，更准确的计算信誉度值，信誉值越接近1，表示其越适合被推荐，通过比较某一矿井(客户)的各客户(矿井)的信誉度值来对其进行最优选择推荐。

2 基于贝叶斯概率煤炭销售推荐流程

基于贝叶斯概率的煤炭销售推荐流程及具体步骤如图1所示。

图1 煤炭销售推荐流程图

步骤1 统计一段时间内大型煤炭企业交易双方的历史数据，若存在n个矿井和k个客户，记录各个矿井和客户的交易总次数及无争议交易次数。

步骤2 根据条件概率公式

计算出对于每个矿井(客户)，其的每个客户(矿井)所占其交易总次数的比例。若上式B代表矿井;Ai代表客户，则P(AiB)表示矿井B与客户Ai的交易次数;P(B)表示矿井 B与所有客户的交易次数;P(Ai)表示客户Ai与矿井B发生交易次数所占矿井B所有交易次数的比例，若上式B代表客户，Ai代表矿井，则)表示客户B与矿井Ai发生交易次数所占客户B所有交易次数的比例。

步骤3 计算每个矿井和每个客户无争议交易比例，即

其中，i=1，2，…，n，j=1，2，…，k。统计得到各矿井和客户的无争议交易比例。

步骤4 通过贝叶斯概率公式计算各交易对象信誉度值，在计算信誉度值时，不同的客户侧重点可能不同，因此对双方交易次数所占矿井(客户)交易总次数比例和双方无争议成交比例设置不同的权值，以满足不同客户需求，设权值系数分别为g，l，则有

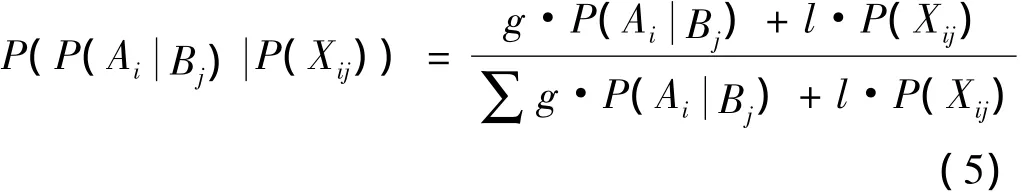
其中，i=1，2，…;j=1，2，…;g，l∈［0，1］，g+l=1。

若Ai表示矿井;Bj表示客户，则 P(P(AiP(Xij)))表示矿井Ai对于该客户Bj所拥有的信誉度值，信誉度值越高，表示这一矿井相较于其他矿井而言与这一客户的交易次数、无争议交易次数越多。因而该矿井更适合这一客户，则会优先将这一矿井推荐给该客户。值越接近1，表示这个矿井越适合这一客户，对于该客户而言，其的信誉度越好，产生贸易纠纷的可能性越小。反之，则表示其的信誉度较差，不适合做最优推荐。若Ai表示矿井，Bj表示客户，同理运销公司根据比较信誉度值向矿井推荐合适客户，信誉度值相同的情况下，则通过比较双方交易次数，推荐交易次数较多者。

3 实验分析

以平顶山天安煤业股份有限公司一段时期矿井与客户的煤炭质量检验数据为例，基于贝叶斯概率理论实现为双方推荐合适的交易对象。该煤炭企业有8个生产煤矿(M1～M8)，与15家战略联盟客户(C1～C15)进行长期煤炭营销合作。对运销公司而言，可将双方的大量历史交易数据作为数据来源，从中进行深入挖掘和统计分析，并最终通过计算和比对信誉度值实现对交易对象的选择推荐，双方一段时期内的交易数据统计，如表1所示。

表1 矿井与客户的交易数据

表 1 中，Mi(i=1，2，3，…，8)表示矿井，Cj(j=1，2，3，…，15)表示客户，中间数据表示两者之间的交易数据，记为“矿井与客户无争议交易次数矿井与客户所有交易次数”，空值表示二者并未交易数据。

根据表1可通过条件概率公式计算得到相对于每个矿井Mi(或每个客户Cj)，其客户Cj(矿井Mi)与之发生交易次数占其所有交易次数的比例。

其次，计算双方无争议交易次数占双方交易次数的比例。然后，通过贝叶斯概率公式计算矿井(客户)中每个客户(矿井)的信誉度，这里权值系数均设置为0.5。最终，若Ai表示客户，Bj表示矿井，当需计算矿井的每个客户的信誉度时，则表示矿井中某位客户所占交易比例，P(Xij)表示该客户与矿井无争议交易所占的比例，则表示该客户对此矿井所拥有的信誉度通过计算，可得到表2数据。

表2 各客户相对某一矿井的信誉度值

对于矿井Mi而言，客户信誉度越大，则该客户越适合推荐。从表2中可看出，对于矿井M1，所有客户中客户C1的信誉度值最大，为0.427，从表1中也可看出对于矿井M1，客户C1的交易量和无争议次数均比较高，运销公司将矿井M1生产的煤推荐给客户C1则较为理想。同理，对于矿井M6，客户C6是其最合适客户，其信誉度达到0.17。从表1中可看出，矿井M6与客户C6进行交易次数较多，且无争议比例也相对较高，所以其成为最适合推荐的交易对象。

同理，当Ai表示矿井，Bj表示客户，表示计算客户的每个矿井的信誉度值表示客户中某一个矿井所占交易比例，P(Xij)表示该客户与矿井无争议交易所占的比例，则P(P(AiP(Xij))表示该矿井对于该客户所拥有的信誉度值，信誉度值越高，表示此矿井越适合该客户，则会优先将这一矿井推荐给该客户。文中将权值系数均设置为0.5，通过计算，可得到表3数据。

表3 各矿井相对某一客户的信誉度值

如表3所示，对于客户C1，矿井M1的信誉度最高，为0.292，如表1所示。对于客户C1的所有交易矿井中，矿井M1是交易次数最多且无争议次数较多的，所以其是最适合推荐给客户C1的矿井。

实验表明，通过矿井和客户交易次数所占矿井(客户)总交易的比例和矿井与客户成功交易比例计算得出的信誉度值能较真实的反映双方历史交易情况，通过比较信誉度值，可实现对运销公司的最优客户推荐，当运销公司需为双方选择交易对象时，推荐给其一个可信度较高的合适客户，进而降低双方交易风险，使其能准确做出选择。而信誉度值的计算又是立足双方以往的交易数据，所以具有较高的可信度。

4 结束语

本文提出了将贝叶斯概率运用到煤炭商品交易双方的交易对象推荐中，通过在大型煤炭企业销售中对交易双方大量历史交易数据的深入分析与挖掘，根据双方交易次数所占各自交易比例，以及双方无争议交易次数比例，并通过设置不同的权值系数，应用基于贝叶斯概率的的方法计算交易双方的信誉度值。并以此为依据实现了为运销公司优化推荐交易对象，降低和减少交易双方的贸易风险，从而达到维护煤炭交易双方利益。

［1］岳福斌.中国煤炭工业发展研究报［M］.北京:中国经济出版社，2013.

［2］闫新庆，王换换，栗青霞，等.基于改进K－Means聚类的煤炭交易者信誉度划分［J］.计算机工程与应用，2014(2):1－8.

［3］张铭，李承军，张勇传.贝叶斯概率水文预报系统在中长期径流预报中的应用［J］.水科学进展，2009，20(1):40－44.

［4］李翔鹰，叶枫.一种基于多贝叶斯算法的垃圾邮件过滤方法［J］.计算机工程与应用，2006(31):114－116.

［5］王洪春.贝叶斯公式与贝叶斯统计［J］.重庆科技学院学报:自然科学版，2010，12(3):203 －205.

［6］谢斌.朴素贝叶斯分类在数据挖掘中的应用［J］.甘肃联合大学学报:自然科学版，2007，21(4):79 －91.

［7］李静梅，孙丽华，张巧荣，等.一种文本处理中的朴素贝叶斯分类器［J］.哈尔滨工程大学学报，2003，24(1):71－74.

［8］许敬，王晓锋.基于贝叶斯概率的运动目标识别方法［J］.南京理工大学学报，2013，37(1):76 －80.

［9］赖英旭，杨震.改进贝叶斯算法在未知恶意软件识别中的研究［J］.北京工业大学学报，2011，37(5):766 －772.

［7］孟宪福，陈莉.基于贝叶斯理论的协同过滤推荐算法［J］.计算机应用，2009，29(10):2733 －2735.

［8］杨静，陈冬，程小红.贝叶斯公式的几个应用［J］.大学数学，2011，27(2):166 －169.

［9］吴奎，周献中，王建宇，等.基于贝叶斯估计的概念语义相似度算法［J］.中文信息学报，2010，24(2):52 －67.

［10］徐光美，杨炳儒，张伟，等.多关系数据挖掘方法研究［J］.计算机应用研究，2006(9):8－12.

［11］HAN Jiawei，MICHELINE K，PEI Jian.数据挖掘:概念与技术［M］.3版.范明，孟小峰，译.北京:机械工业出版社，2012.

［12］PEDRAM M，BEHZAD T，MAJID A J，et al.Application of bayesian in determining productive zones by well log data in oil wells［J］.Journal of Petroleum Science and Engineering，2012(94－95):47－54.