EMD样本熵在滚动轴承信号复杂性度量中的应用
王 季 , 楼军伟 ,2, 李贵子, 朱 琳
(1.甘肃省机械产品检测与技术评价重点实验室,甘肃 兰州 730030;2.兰州理工大学机电工程学院,甘肃 兰州 730050)
0 引 言
轴承振动信号具有非线性、非平稳、不同复杂性等特征,直接进行傅里叶变换难以揭示频率分量随时间的变化情况;短时傅里叶变换、小波变换等能够在时间和频率上建立信号的分布,可以有效提取特征频率,然而它们是先验性的,自适应能力差。经验模态分解(empirical mode decomposition,EMD)无须预先设定任何基函数,是一种后验的、自适应的方法,按时间序列将信号多尺度分解为多个内禀模态函数(intrinsic mode function,IMF),每个 IMF 包含了原信号不同尺度上时间序列的局部特征[1-4]。度量信号复杂性的方法有Lempel-Zi复杂度、近似熵、样本熵和频带熵等。Yan 等[5]将近似熵(appropriate entropy,ApEn)用于轴承状态监测并取得较好的效果。Pincus[6]提出样本熵(sanple entropy,SampEn),是近似熵的改进算法,其优越性在于可以较好地依赖时间序列长度,不存在比较自身数据段的问题;参数改变时结果一致性较好;能更精确度量非线性信号在时间序列上的复杂性等。这个方法广泛应用于信号处理[5-9]。
本文采用EMD结合样本熵的方法,分析它们的算法和样本熵合适数据长度的选取。对不同故障程度的滚动轴承信号应用样本熵和EMD样本熵的效果进行比较,发现后者度量信号复杂性效果较好,其变化趋势与信号随故障变化的趋势一致。该方法可用于滚动轴承运行状态监测和预判。
1 EMD算法流程
由N E Huang等[10]提出的经验模态分解基于如下假设:任何复杂信号都是由一些不同的、相互独立的内禀模态函数组成;信号不论是线性、非线性、非平稳的,都具有相同数量的极值点和过零点,或最多相差一个;上下包络线关于时间轴局部对称,任何两个模态之间相互独立。按此假设对输入的信号x(t)进行分解,也称为“筛选过程”。图1为EMD分解流程图。
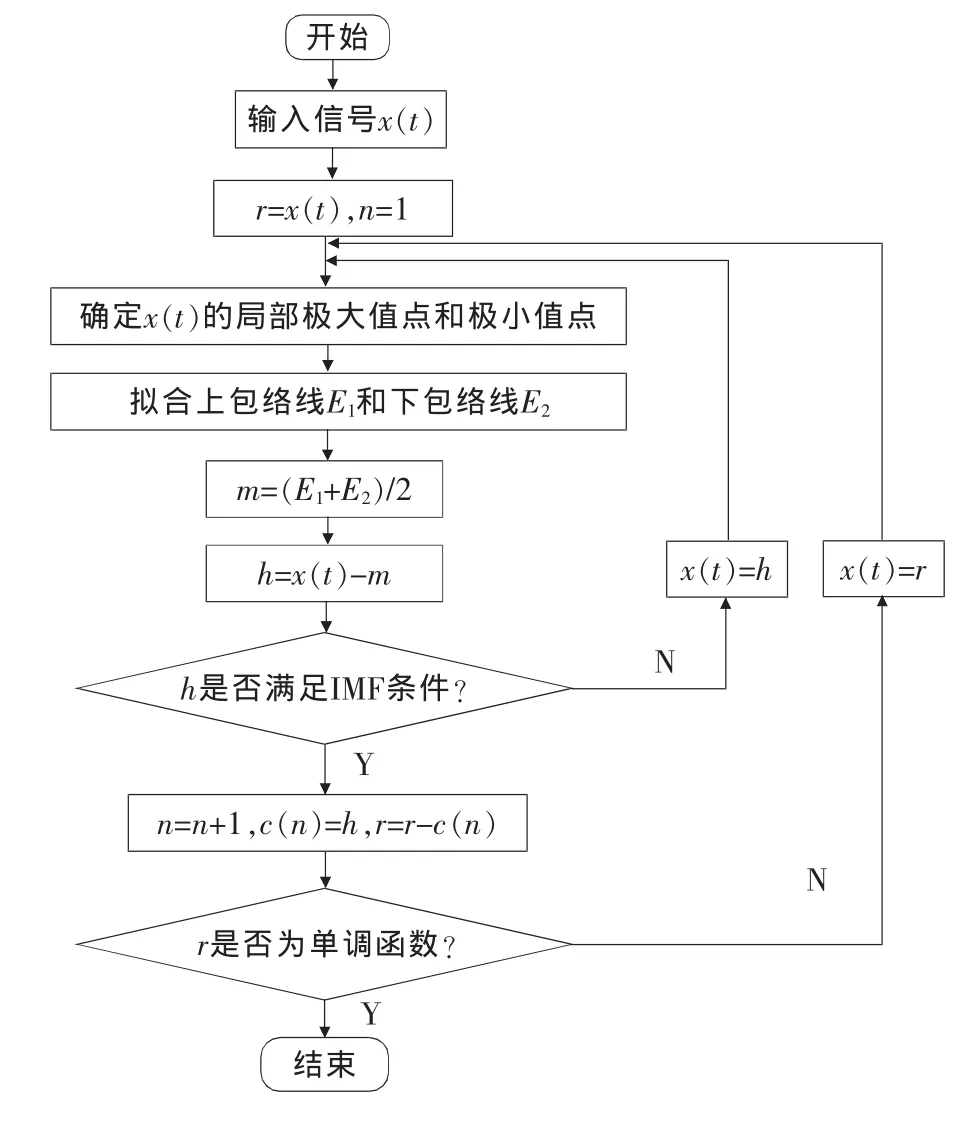
图1 EMD分解流程图
1)整个循环中,上下包络线Ei、Ej是用 3次样条曲线连接信号x(t)的所有局部极大值点和所有局部极小值点得到。第一次求上下包络线平均值记为m1(t),令:

如果h1(t)是第一个分量 IMF1,则循环停止。
2)若不是,则按流程图所示返回以h1(t)为原始信号继续求上下包络线以及平均值m2(t),令:

判断h2(t)是否为IMF分量,如此循环n次,直到:

式中hn(t)满足 IMF 分量要求。
3)将hn(t)分离出来,记c1(t)=hn(t)为信号x(t)的第一个IMF分量,得到:

4)判断r1(t)是否单调,若不是,再按流程图所示重复以上步骤n次,直到得到信号x(t)所有IMF分量为止。
即:
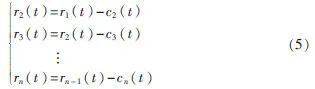
5)原始信号x(t)组成为

式中rn(t)为残余函数,代表信号平均趋势。
EMD从信号时间序列出发,把信号中特征模态从最小到最大逐步分离出来,使波形轮廓更加对称,整个过程中无需预先设定任何基函数,是一种多尺度、自适应的方法,适合于分解非线性、非平稳滚动轴承信号。
2 样本熵
2.1 样本熵算法
1991年Pincus提出了近似熵,但是近似熵存在自身数据匹配等问题。于是Richman[9]在近似熵的基础上提出了不需要比较自身数据的样本熵。算法步骤如下:
对EMD分解后的其中一个分量c1(t),设其具有N个数据点。预先定义相似容限r,通常取r=0.1~0.25SD(x),SD 表示x(N)的标准差,模式维数m=2。
1)重构m维向量:
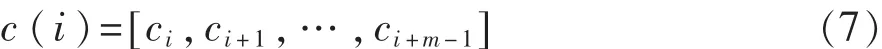
其中i=1,2,…,N-m。
2)计算c(i)与c(j)元素间的距离dij,dij为对应元素差值绝对值的最大值:

其中k=0,1,…,N-m。


4)求 Bim(r)的平均值:
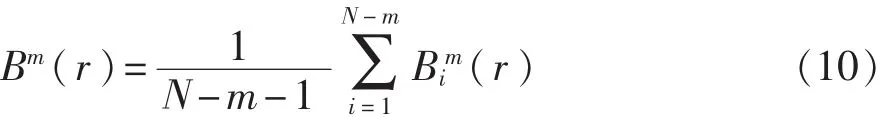
5)根据维数 m,重复 1)~4)得到 Bim+1(r)和 Bm+1(r)
6)最后计算当 N 为有限值时 SampEn(m,r)

可见样本熵是用一个非负数来表示一个时间序列的复杂性,越复杂的时间序列样本熵越大,越规则的时间序列样本熵越小。
2.2 数据长度选取
当维数 m=2,r=0.25SD(c)时,如何选取数据长度N,图2给出了验证。

图2 数据长度对样本熵结果稳定性影响
当数据长度小于500时,样本熵计算结果波动比较大,当数据长度大于1000以后,样本熵计算结果趋于稳定。结合实际测取的轴承信号,本文选取数据长度为2500,使计算速度、精度和稳定性都有保证。
综上可知,EMD能对信号按时间序列做多尺度分解,样本熵能度量时间序列的复杂性,可将二者结合起来对信号进行多尺度、深层次分析,即本文采用的EMD样本熵方法。
3 实例应用比较分析
选取的电机轴承型号为6205,电机负载为1.45 kW,转速为1750r/min时采集正常和不同故障下内圈、外圈的振动信号。其中故障程度又分点蚀直径为 0.17,0.30,0.71mm 3 种,深度均为 0.28mm,分别记为故障1,故障2,故障3。
3.1 样本熵
对故障1和2信号按第2部分样本熵算法,取m=2,r=0.25SD(c),N=5 000,直接计算样本熵,得到结果如表1所示。

表1 不同故障时信号样本熵
根据表中数据可知,在不同故障程度下,样本熵内、外圈明显不一样,相差至少在百分位以上,在Matlab中作图曲线间隔较大。但是在故障2下,出现内、外圈熵值差仅千分位的情况,在误差范围内不容易区分。原因是样本熵是单一尺度上的计算,而轴承信号是非线性、非平稳的,样本熵在处理时有局限性,无法进行深层次计算。
3.2 EMD样本熵
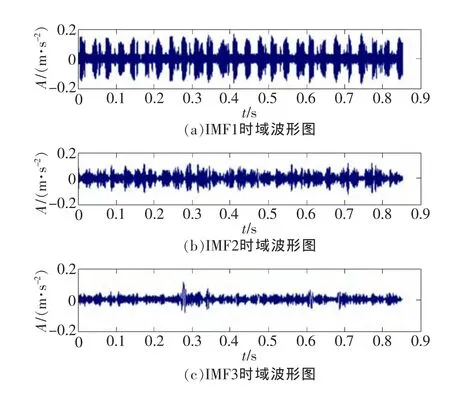
图3 正常轴承信号3层EMD分解

图4 故障1内圈信号3层EMD分解
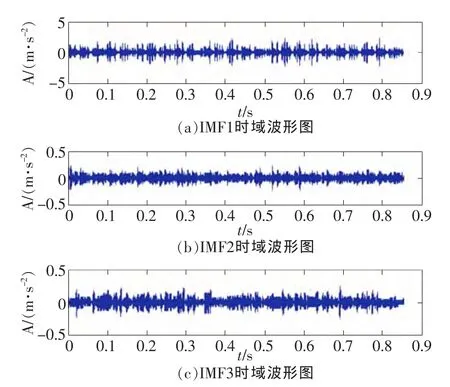
图5 故障1外圈信号3层EMD分解
将所有数据分别按EMD分解流程进行3层分解,由于篇幅有限给出了部分信号IMF分量波形。图4,图5是故障1情况下内圈、外圈信号3层IMF分量。与图3正常轴承比较,故障情况下信号较复杂,并且内圈信号较外圈复杂。
再计算正常、故障1,故障2,故障3下内、外圈信号每一分量的样本熵,结果如表2~表5所示。
1)从表2~表5可见,各分量EMD样本熵故障轴承明显大于正常轴承,特别是内圈EMD样本熵更大,说明信号中产生新模式故障信号。
2)故障情况下,任何一个分量EMD样本熵内圈较外圈大,与内、外圈EMD 3层分解图4、图5波形变化趋势一致。

表2 正常轴承EMD样本熵

表3 故障1时EMD样本熵
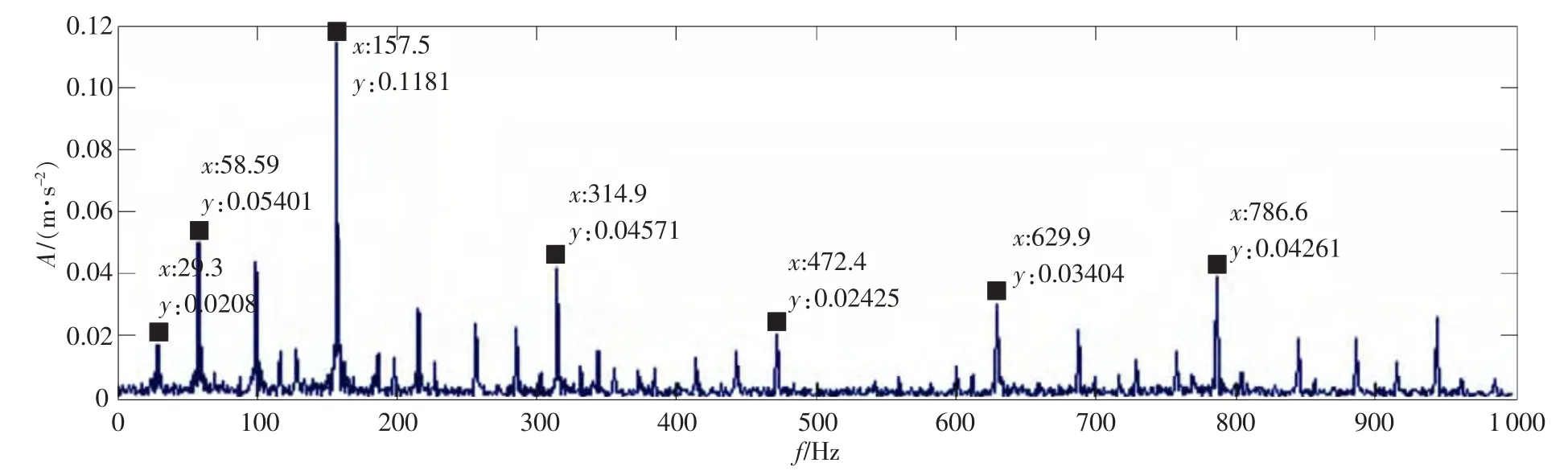
图6 故障1时IMF1分量0~1000Hz包络谱
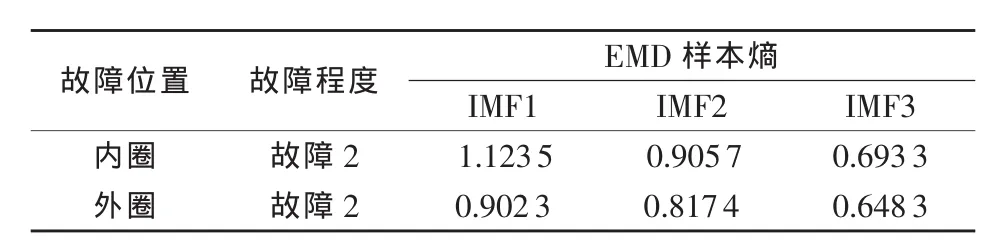
表4 故障2时EMD样本熵

表5 故障3时EMD样本熵
3)在故障情况下,各分量的EMD样本熵均是IMF1>IMF2>IMF3,与EMD分解越后面的层信号相对越简单一致。
4)从EMD样本熵值看故障1时较故障2时的大,较故障3时的小。说明故障初期的EMD样本熵较大,一定程度后样本熵减小,到故障严重时样本熵又变大,符合轴承故障对信号影响的变化趋势。
5)表3~表5中不管是同种故障模式还是不同故障模式下,内、外圈各分量EMD样本熵相差在百分位以上,与表1中差值仅在千分位形成明显对比。这表明EMD多尺度分解弥补了样本熵单尺度分析,效果比样本熵好。
4 包络谱分析
上文提到,EMD样本熵越大信号越复杂,产生新模式的概率越大。为此,选取故障1时内圈的IMF1分量进行包络谱分析,图6为该分量0~1000Hz的包络谱。
通过计算得知电机轴转频29.12Hz,内圈固有频率157.7Hz。包络谱中标记的频率值与计算频率值几乎一致。损伤时出现电机转频29.3Hz及其2倍频,内圈固有频率157.5Hz最高峰值,以及2倍频、3倍频、4 倍频、5 倍频分别为 314.9,472.4,629.9,786Hz。 在157.5Hz两边出现了间隔为29.3Hz的边频带。包络谱得出诊断结果的同时也验证了EMD样本熵越大信号越复杂性,产生故障模式的概率越大。
5 结束语
本文采用EMD样本熵度量滚动轴承信号复杂性,实例比较结果表明:
1)EMD是自适应的,能对时间序列进行多尺度分解的方法,有效地弥补样本熵单一尺度上分析的缺陷,二者结合能有效度量信号复杂性。
2)分别计算了不同故障下的滚动轴承信号样本熵和EMD样本熵,比较结果表明后者度量信号复杂性效果更好,在不同损伤程度时熵值明显不一样。
3)在故障程度逐渐变大的情况下,EMD样本熵先大-后小-再大的变化趋势准确反映了信号随故障变化的趋势,在轴承状态变化预测方面有较大的应用价值。
[1] 赵荣珍,杨娟,冯如只,等.信息熵与广义集合集成的轴承-转子系统故障辨识方法[J].兰州理工大学学报,2010,36(4):28-32.
[2] 胥永刚,何正嘉.分形维数和近似熵用于度量信号复杂性的比较研究[J].振动与冲击,2003,22(3):25-27.
[3] 苏文胜,王奉涛,朱泓,等.基于小波包样本熵的滚动轴承故障特征提取[J].振动、测试与诊断,2011,31(2):162-166.
[4] 王小玲,陈进,从飞云.基于时频的频带熵方法在滚动轴承故障识别中的应用[J].振动与冲击,2012,31(18):29-32.
[5]Yan,Gao R X.Approximate entropy as a diagnostic tool formachine health monitoring[J].Mechanical Systems and Signal Processing,2007,21(2):824-839.
[6] Pincus S M.Approximate entropy as a measure of system complexity[J].ProNatl Acad Sci,1991(88):2297-2301.
[7] Lake D E, Richman J S, Griffin M P, et al.Sample entropy analysis of neonatal heart rate varability[J].Am J Physiolregul Integrcomp Physiol,2002,283(3):789-797.
[8] Pincus S M.Assessing serial irregularity and its implica-tions for health[J].Ann N Y Acad Sic,2002(954):245-267.
[9] Richman J S,Moorman J R.Physiological time series analysis using approximate entropy and sample entropy[J].Am J Physiol Heart Physio,2000(278):2039-2049.
[10]Huang N E, Steven Z H, Long R,et al.The empirical modede composition and the Hilbert apectrum for nonlinear and nonstationary time series analysis[J].Proc R Soc Lond A,1998(454):903-995.

