透视仿射对应在画法几何中的应用与研究

张世海（甘肃交通职业技术学院，甘肃 兰州 730070）

1 引言

在画法几何中，求解平面与立体表面的截交线以及曲面立体截交线的轴测投影，大部分情况下截平面都处于特殊位置平面或立体表面在某一个投影面上具有积聚性，所用的方法通常有积聚性法、辅助平面法、辅助球面法和换面法等，求解过程及作图相对比较简单。但是如果平面是一般位置平面或立体的表面无积聚性时，如果仍然采用上述方法，则作图相对比较繁琐，而且不易保证作图的准确性。相反，应用透视放射对应法求解二次曲面的截交线、截交线的轴测投影等问题，则是一种行之有效的方法[1]。

2 透视仿射对应的基本理论

2.1 两平面场透视仿射对应的建立

透视放射对应是由一次平行投影所建立的两平面场之间的仿射变换[2]。如图1所示，设已知相交两平面为P和P1，两平面的交线为SS，直线L为投影方向。

图1 透视仿射对应的建立

通过平面P上的两点A、B，作直线L的平行线，与平面P1相交于A1、B1，这样平面P上的点和平面P1上的点就建立了一一对应的关系，这种对应就是P到P1的透视仿射对应。其中，A和A1称为对应点，直线AB和A1B1称为对应直线，直线L称为对应方向，两平面的交线SS上的点都是自身对应的，称为二重点，如点MS。显然，交线SS是两个对应平面上二重点的轨迹，称为对应轴。

2.2 透视仿射对应的基本性质

由于透视放射对应采用的是平行投影的方法，所以，透视放射对应具有初等画法几何中平行投影的基本性质，即同素性、从属性、平行性和等简比性。

1）同素性 平面P上的点对应平面P1上唯一确定的点，平面P上的直线对应平面P1上唯一确定的直线。

2）从属性 若点属于直线，则其对应点也属于该直线的对应直线。

3）平行性 平面P上互相平行的两条直线，在其P1上的对应直线也平行。

4）等简比性 直线上三个点所组成的简比，等于其对应直线上三个点的简比。

2.3 两平面场仿射对应的主方向

在仿射对应中，角度是一个变量，也就是说两条相互垂直的直线，经过仿射对应后，其对应直线不一定保持相互垂直的关系。但是，如果一对互相垂直的直线经过仿射对应后的对应直线仍然垂直，那么这两对直线所决定的方向就分别称为场P和P1的主方向。

如图2所示，对应方向与对应轴倾斜相交，

设透视仿射对应由对应轴SS和一对对应点A和A1确定。过对应点连线AA1的中点M作垂直于AA1的直线，与对应轴相交于点N，以点N为圆心，NA或NA1为半径作一辅助圆，与SS相交于1（11）、2（21），连接1A、2A和11A1、21A1。这时，直线1A、2A分别对应于直线11A1、21A1。由于∠1A2和∠11A121均为直径所对应的圆周角，所以1A⊥2A，11A1⊥21A1。两对应直线1A、2A和11A1、21A1所决定的方向即为场P和P1的主方向。

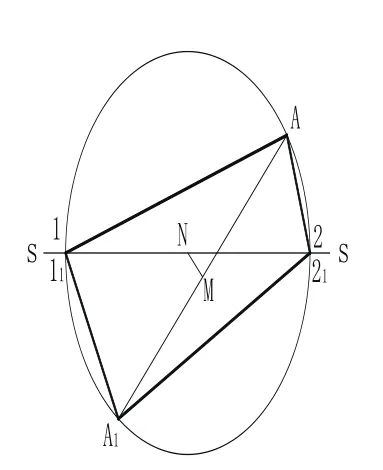
图2 仿射对应的主方向

3 透视仿射对应法的应用

3.1 应用透视仿射对应法求截交线

例 如图3所示，求平面P与三棱柱的截交线。

1)作截平面P的对应轴SS。在迹线平面上任取一点N，过N作水平线，得二重点nS，连接PXnS，为P面的对应轴SS，这样就建立了以SS为对应轴、点n＇和n为对应点的透视放射对应。

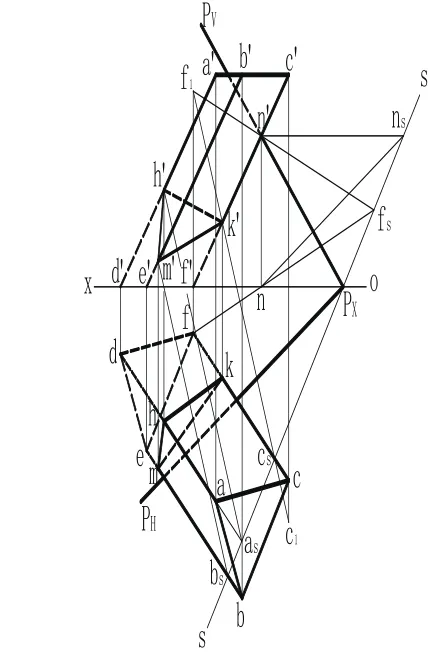
图3 求平面P与斜三棱柱的截交线

2)作棱线cf的对应直线c1f1以及c1f1与c＇f＇的交点k＇。可先求出f的对应点f1，连接fn并延长交对应轴SS于fS点，连接fS错误！链接无效。并延长，与过f点所作平行于n n＇（对应方向）的直线ff1交于f1点，f1点即为f点的对应点。同理，可作出c点的对应点c1，因fc交 SS于cS，连接cS f1，则c1必在cS f1上，且与c对应。c1f1与cf即为一对对应直线，c1f1与c＇f＇的交点k＇即为CF棱线与P面交点的正面投影，由k＇求得k。

3)由于三棱柱的棱线AD、BE、CF相互平行，故其ad、be、cf的对应直线a1d1、b1e1、c1f1也互相平行。所以，分别求出ad、be与ss的交点as、bs，过as、bs作cs f1的平行线与a＇d＇、b＇e＇相较于h＇、m＇点，由h＇、m＇点求出h、m点。

4)连接△k＇h＇m＇和△khm，即为截交线的两面投影，并判别可见性。

3.2 应用透视仿射对应法求截断面的实形

求截断面实形所用的方法通常有换面法、旋转法和重合法等，但这些方法往往需要作出截交线的投影才能求出截断面实形。而采用透视仿射对应法，则可在已知截平面和曲面的情况下直接求出截断面的实形。

如图4所示，平面P与斜圆柱面相交，求截断面的实形。

图4 求平面P与斜圆柱截交线的实形

由于截交线与底圆均在斜圆柱面上，而且圆柱面上所有素线相互平行，因此截交线椭圆与圆柱底圆构成透视仿射对应，将P面上的椭圆旋转到与H面重合时，该椭圆与底圆仍然构成透视仿射对应，对应轴为PH，该椭圆即为截断面的实形。

1）作辅助正垂面R，求出平面P与圆柱轴线的交点O（o，o′）。

2）采用旋转法[3]求出P面绕PH旋转到与H面重合时的新位置O0。

3）由对应点为O0、O2，求出对应的主方向，从而确定实形椭圆的长、短轴，再作出椭圆。

3.3 应用透视仿射对应法求作平行于坐标面的圆的斜轴测投影

对于平行于坐标面的圆，总存在两条平行于坐标轴且相互垂直的直径，作出此两条直线的斜轴测投影，即为所求椭圆的一对共轭直径。通过建立圆和欲求椭圆之间的透视仿射对应关系，即可确定椭圆的长短轴，从而完成平行于坐标面的圆的斜轴测投影。

图5 求椭圆的长短轴

如图5所示，利用椭圆外切平行四边形的一边M1N1作为透视仿射对应轴，作与椭圆及外切平行四边形对应的圆和外切正方形，找出圆心O，O与O1为一对对应点，利用该对应中的主方向求得椭圆的长轴E1F1和短轴G1H1，完成椭圆。若A1B1=2C1D1，∠A1 O1 C1=45°，即为国标推荐的斜二测水平面上的椭圆。

3.4 在轴测投影中作曲面立体的截交线

在轴测投影中求作曲面立体截交线，通常是先在多面正投影图上作出截交线，然后再根据截交线上各点的坐标作出截交线的投影。这种方法虽比较容易掌握，但在作多面正投影图时，容易产生累计误差，较难求出截交线上的特殊点，无法保证作图的准确性[4]。而利用透视仿射对应法，则可在轴测投影图上直接作图，能克服上述缺点。

如图6所示，正圆柱被一般位置平面P所截切，利用透视仿射对应法，求出截交线椭圆的轴测投影（正二测E）。

图6 求圆柱截交线的轴测投影

先任意作轴测平面Q，并采用XOY坐标重合法作出圆柱底圆的实形。坐标面的重合位置X0O0Y0和其轴测投影X1O1Y1成透视仿射对应（称为对应Ⅰ），QX1QY1为对应轴，O1、O0为一对应点，O1X1和O0X0、O1Y1和O0Y0是相互垂直的成对应的直线。过底椭圆中心c1作k1l1∥QH1，则在与它对应的直线K0L0上便能找到与c1对应的点C0，从而作出圆柱底圆的实形。

截平面P上各点的轴测投影和其在XOY坐标面上的次投影成透视仿射对应（称为对应Ⅱ），PH1(PX1PY1)为对应轴，PZ1和O1为一对应点。由于P面上截交线椭圆上各点的次投影都处在圆柱底椭圆上，因此该两椭圆便是对应Ⅱ中的一对对应图形。由于PV1和O1X1、PW1和O1Y1也是相互成对应的直线，因而可求得与k1l1对应的K1L1以及与c1点对应的C1点，C1点即为截交线椭圆的中心。K1L1与圆柱轴测轮廓线的交点A1、B1便是与a1、b1对应的点，因而也就是截交线椭圆与轴测轮廓线的切点[5]。

由此可见，圆柱底椭圆（中心为c1）与其实形圆（中心为C0）成对应Ⅰ，又与截交线椭圆（中心为C1）成对应Ⅱ，这两个对应具有公共的对应方向，因而截交线椭圆与实形圆之间也成透视仿射对应（称为对应Ⅲ），PZ1和O0、C1和C0均为相对应的对应点，PV1和O0X0、PW1和O0Y0为对应直线，它们的交点为M、N点，MN即为对应Ⅲ的对应轴。以上三个对应的对应轴应具有公共点J。作C1C0的中垂线，找出对应Ⅲ的主方向，从而求出截交线椭圆的长轴D1E1和短轴F1G1，最终作出截交线椭圆的轴测投影。

4 结 语

由于透视仿射对应是平行投影下的两场之间的变换，其基本理论和性质比较简单，而且投影方向不受垂直的限制[6]，可以根据需要灵活确定。因此，对于求作截交线、截交线实形和圆的斜轴测投影等问题比较简洁、准确，是一种行之有效的的方法。

[1]张桂梅.徐临洪.曾接贤.基于透视仿射变换研究画法几何中的截交线问题[J].南昌航空工业学院报，2003，第2期:68-70.

[2]朱辉.曹桄.张士良.高等画法几何学[M].上海:上海科学技术出版社，1985:1-495.

[3]郑国权.道路工程制图[M].北京：人民交通出版社，2002:1-366.

[4]戴志国.应用仿射变换求二次曲面交线特殊位置点的探讨[J].大连轻工业学院学报，1995，14（2）:28-31.