Aprior 算法在海滨观测数据相关性检验中的应用

戴文娟，雒伟民，陈靓瑜，张 峰，高静霞，黄雅馨

（国家海洋局东海信息中心 上海市 200120）

数据的质量控制是指采用一定方法、模型和参数，判断资料质量可靠性与准确性，并进行质量标识的处理过程，数据质量控制是数据质量评估的基础。对海洋观测数据进行适当的处理和质量控制，能够妥善解决资料中可能存在的错误，提高资料的可靠性与准确性。目前海洋数据质量控制中选用的检验方法主要包括两类：第一类是常规检验，主要有位置检验、气候学范围检验、合理性检验（季节性、局地性）、时间连续性、异常天气限制、双传感器检验、内部一致性检验等方法构成；第二类为特殊检验，主要由相关检验、人工比对等方法构成[1]。第一类常规检验均针对某一特定的观测要素，目前也是运用较多的检验方式。而第二类特殊检验是针对两个或者多个观测要素在同一时段内产生数据的相互检验，因观测要素性质不同、变化规律不同因而为相关检验带来了一定的复杂度。

正因为相关检验的复杂性，目前在海滨观测数据质量控制中尚未有较通用的相关检验方法，一般是通过人工气象预报经验对常规检验中可疑的数据进行相关检验。每年6-9月份是东海台风、风暴潮等极端天气频发时刻，当极端天气过境时，风浪数据往往可能突破正常的合理性范围或产生非连续性突变，此时只有相关检验就能较准确地判断该数据变化是否符合这种极端天气的特性从而能够判定当前数据采集传感器是否处于正常工作状态（极端天气带来数据采集传感器故障或异常频率较高）。

选择经典的关联规则Aprior 算法解决海滨数据相关性检验的问题，将海滨观测数据属性分成3 类：小于等于Minin、大于Minin且小于Maxin、大于等于Maxin。通过历史数据的挖掘建立这不同观测要素3 种属性的最小支持度和置信度，当极端天气出现时通过比较不同观测要素出现变化的频繁性是否与历史数据挖掘出的最小支持度和置信度一致，来判断观测要素是否符合相关性检验[2-4]。

1 Apriori 算法

Apriori 算法是挖掘关联规则的一种重要方法，该算法属于递归统计计算，枚举出其可能出现的所有频繁项集，非常适用于变化规律较一致的海滨观测数据。只需要一次性自下而上遍历整个数据库，建立频繁集出现规则，以后每次相关检验只需要调用相应规则比对即可[5，6]。

1.1 关联规则的定义

定义1，选择一个事物数据库D，D = {I1，I2，…，Ij，…，In}，I 是其中每个事物集，而Ij则是其中一项事物，它可以由若干个项目构成，可以表示为{X1，X2，X3，……}，我们称为项目集X，如果X 属于Ij，那么称事物Ij包含项目集X。

定义2，事物数据库D 包含的项目集X 的个数，我们称为项目集X 的支持数，用α（X）表示。用sup port（X）表示项目集X 的支持度，支持度是项目集X 的支持数和数据集D 的事物个数的比值。公式如下[7，8]：

定义3，如果项目集X 的支持度大于用户定义的最小支持度，则称X 为频繁项目集。

定义4，如果同时存在A，B 两个项目集，并且A 和B 中都包含相同的元素，就称A圯B 为关联规则。sup port（A圯B）为关联规则的支持度，可以表示为sup port（A 圯B）= sup port（A∪B）。并且用confidence（A圯B）表示关联规则的置信度，推导公式为：

1.2 关联规则的定理

假如事务数据库D 有2 个项目集，分别为项目集A 和项目集B，根据以上定义，我们还可推导出如下定理：

定理1：如果项目集A 包含项目集B，也就是A勐B，一定有项目集B 的支持度大于等于项目集A 的支持度，也就是sup port（B）≥sup port（A）。

定理2：如果项目集A 包含项目集B，也就是A勐B，并且项目集B 不是频繁项目集，那么A 也一定不是频繁项目集；反过来也同样，如果A 是频繁项目集那么B 也一定是频繁项目集。

1.3 关联规则挖掘

Apriori 算法的基本思想是：首先找出所有的频集，这些项集出现的频繁性至少和预定义的最小支持度一样。然后由频集产生强关联规则，这些规则必须满足最小支持度和最小可信度。然后使用第1 步找到的频集产生期望的规则，产生只包含集合的项的所有规则，其中每一条规则的右部只有一项，这里采用的是中规则的定义。一旦这些规则被生成，那么只有那些大于用户给定的最小可信度的规则才被留下来。具体算法步骤如下。

（1）扫描整个事物数据库D，找到候选项集1-的集合A1。

（2）根据最小支持度sup_min，从找到的候选项A1中产生频繁项集1-的集合I1。

（3）如果k 莨1，则重复步骤4、5、6。

（4）对Lk进行连接和减枝操作，生成候选（k+1）-项集的集合Ak+1。

（5）根据最小支持度sup_min，从Ak+1中产生频繁（k+1）-项集的集合Lk+1。

（6）如果Lk≠覫，则K=K+1，转到步骤4，否则转到步骤7。

（7）根据最小置信度con_min，由频繁项集产生强关联规则。

2 海滨观测数据中关联规则模式提取

根据关联规则的基本概念和Apriori 算法的基本思想，结合海滨观测历史数据，可以得到海滨观测数据关联规则模式提取的基本步骤。

（1）扫描海滨观测数据库，确定Ij为海滨月报数据文件T011、T012、T021、T022、T023、T031、T051、T052、T053、T054，各种文件包含的不同观测要素见表1。

根据质量控制的基本原理，首先确定每种要素其相关检验的数据来源，海表温度、盐度数据来源于T012 文件；潮位数据来源于T023 文件；海浪数据来源于T031 文件；气压、气温相对湿度、降水量数据来源于T054 文件；风速风向来源于T053 文件。最终要素间的相关性检验就是对T012、T023、T031、T053、T054 文件数据提取后进行文件间的相关性检验。

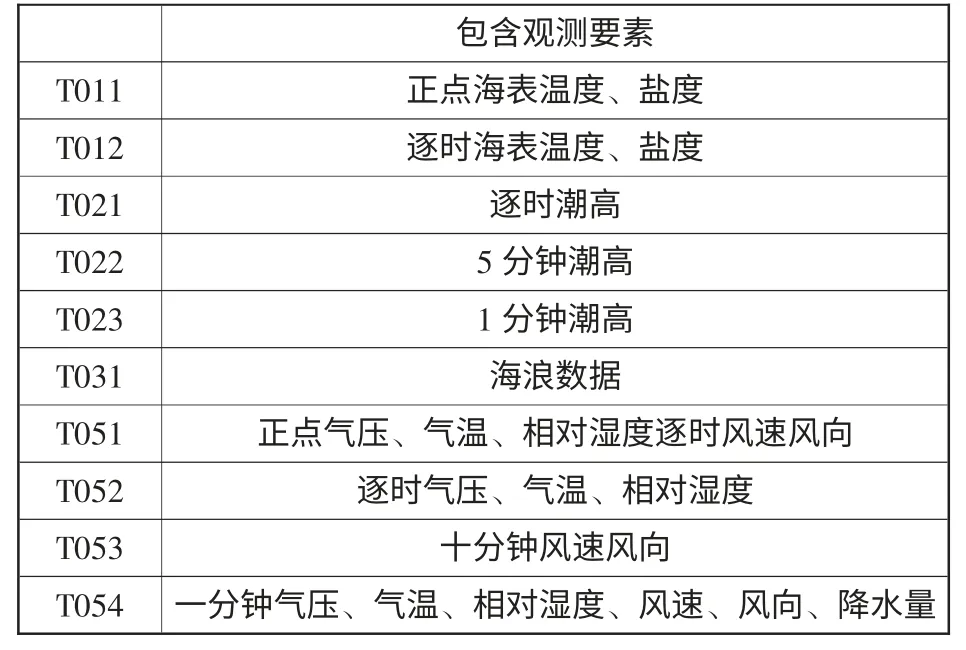
表1 海滨月报数据观测要素表

（2）通过每个从历史资料（2006-2012年海滨观测数据）中挑选出该海洋站该要素的历年当月极大值的平均值（Maxin）和历年当月极小值的平均值（Minin），作为该站该要素属性的边界。将所有观测要素赋予3 类项目属性，小于等于Minin、大于Minin且小于Maxin、大于等于Maxin。不同情况的观测要素的项目属性表示如表2 所示，观测属性的代码赋值如表3 所示。

表2 海滨观测要素数值项目属性表示表

表3 海滨观测要素属性对应代码

（3）通过项目属性中数值“1”计算不同观测要素的频繁项集并计算最小置信度con_min，即由频繁项集产生强关联规则。若推理得出降水量的最小置信度con_min 大于1，那么其含义为降水量的X 项目非（0，0，1）。将1.3 章节的算法代入选择某海洋站的某月部分数据进行实验计算结果如图1。

图1 海滨观测相关性检验事例数据计算结果

选择东海区某观测站点2006-2012年间观测月报数据的统计计算部分强关联规则如表4。

表4 海滨观测要素的部分强关联规则

3 模式在海滨观测数据相关检验中的应用

2012年8月东海区沿海遭遇达维、海葵、天秤、布拉万等多个台风登陆，该月海滨观测数据报文通过常规质量控制软件发现多处数据可疑，为了进一步判断该数据可疑是观测真实情况还是因仪器故障等生成的无效数据，因此对该月数据报文采用基于Apriori 算法的关联规则模式进行相关性检验。

分别导入可疑数据较多的3 个海洋站崇武（CWU）、东海大桥（DHQ）、大戟山（DJS）。导入每个海洋站的T012、T023、T031、T053、T054 5 个文件。

选择台风过境时最可能出现的风速增大模式对可疑数据进行相关性检验。选择需要相关性检验的要素崇武站是温度、潮位，东海大桥站是温度、盐度、波浪，大戟山站是潮位、降水量。

经检验崇武海洋站可疑的温度潮位变化，符合相关性检验，当风速突然增大时温度下降速度较快，潮位有较大的上升。

图2 崇武站传统检验提示数据可疑

经检验东海大桥海洋站可疑的温度、盐度、波浪数据不符合相关性检验，当风速突然增大时温度上升，盐度增大后降低，波高无明显变化，周期变小，经于当地海洋站联系因台风导致传感器异常故障，该月所有数据均做缺测处理。

经检验大戟山海洋站可疑的潮位和降水量，符合相关性检验，当风速增大时潮位有较大变化，降水量突增。

4 结 语

海滨观测数据质量控制是海洋防灾减灾领域的一项重要工作，海洋预报及海洋变化研究对数据的质量均有较高的要求。在实际工作中海滨观测数据质量控制正通过历史经验的积累逐步走向自动化、智能化。数据挖掘是从大量的数据中抽取出隐含在其中不为人所注意的有用信息的过程，关联规则时数据挖掘领域重要的研究方向。而海滨观测的各种数据并不是相互孤立的，在同一时间内其不同观测要素之间有着强烈的相关性，发掘其之间的相关性作为其相关性检验的基础是该研究的核心思想[9，10]。

实验数据证明通过选择不同场景模式进行相关性检验，可以较好地对常规数据质量控制中的可疑数据进一步质量控制，从而判断数据是否可用，可以作为今后工作中数据相关性检验的方法。然后该方法还有较多缺陷，例如规则模式无法通过人工智能的自学习进行自动更新，相关性检验仅能判断数据变化的趋势性，而无法更加精确地研究数据变化的范围，该缺陷有待后续进一步研究。

[1] 于婷，刘玉龙，等.实时和延时海洋观测数据质量评估方法研究[J].海洋通报，2013（6）：610-615.

[2] 李广霞，思亮.关联规则发现方法研究[J].软件导刊，2014（4）：14-17.

[3] 毛国君，段立娟，王实，等.数据挖掘原理与算法[M].北京：清华大学出版社，2007.

[4] 金蛟.回归模型的相关性检验[J].北京师范大学学报，2007（43）：591-594.

[5] 李宏伟.基于关联规则的数据挖掘技术在中长期水文预报中的应用[J].人民珠江，2013（6）：21-25.

[6] 吕杰，林陈是维.基于相关性度量的关联规则挖掘[J].浙江大学学报，2012（39）：285-288.

[7] 俊芳，谢益武，周生宝.关联规则相关性的度量[J].计算机应用，2007（4）：891-896.

[8] 张玉芳，熊忠阳，彭燕，等.基于兴趣度含正负项目的关联规则挖掘方法[J].电子科技大学学报，2010（3）：407-411.

[9] 廖琴，郝志峰，陈志宏.数据挖掘与数学建模[M].北京：国防工业出版社，2010.

[10] 尚志，粱宝华，赵小龙，等.正负关联规则量化方法[J].计算机工程，2009（15），74-76.