基于粗糙度的三维网格模型数字水印

朱利利，张建勋，汪 波

(重庆理工大学计算机科学与工程学院，重庆 400054)

近年来，随着数字技术的普及，版权问题成为关注的焦点。数字水印一般是指向多媒体数据中嵌入不可察觉的信息从而达到嵌入水印的目的。向图像、音频、视频加入水印的技术已经成熟，而在三维模型中嵌入水印信息的技术还有待研究，三维模型的版权保护仍然具有挑战性。

Ohbuchi于1997年提出三维模型数字水印算法［1］，随后又提出三角形相似比、四面体体积比等嵌入算法，将三维数字水印推上了新的高度，开启了三维数字水印研究的新思路和方法。

文献［2］提出了基于高斯主曲率分割实现三维模型的分割，但是无法满足对粗糙和平滑部分的划分。Karni与Gotsman提出采用拉普拉斯矩阵度量粗糙度［3］，利用拉普拉斯矩阵平滑模型，然后与原模型对照的方法，缺点是只针对点，没有考虑一定范围的粗糙度。Cheng通过计算三维网格模型相邻面的角度来衡量粗糙度。喻志强等［4］利用法线随顶点改变引起的改变量决定嵌入强度，算法鲁棒性强，但是不能保证嵌入在粗糙区域，从而致使水印可见。

本文提出了一种基于粗糙度的三维网格模型数字水印算法。预处理阶段利用一环邻域质心的法向量和加权法向量的夹角来选择候选顶点，从而剔除不符合条件的顶点。嵌入阶段使用包围盒策略得到中心，利用点到中心的距离分块，根据粗糙度得到权值，从而选择嵌入顶点。实验结果表明，在保证鲁棒性的条件下，三维模型数字水印的不可感知性得到了提高。

1 水印的嵌入与提取

1.1 基本原理

人类视觉系统HVS对高频不太敏感，在保证人眼不能察觉的情况下，可以改变信号强度［5］。人眼对平滑区域的敏感度较强，对边缘和纹理区域的敏感度要相对弱些。因此可以在人眼不敏感的区域嵌入水印，从而增强水印的鲁棒性。

在机械制造中的粗糙度是指加工后零件表面的较小间距和微小峰谷凹凸不平程度，两波峰和波谷之间的距离很小。它是微观几何形状误差，粗糙度越高，表面越粗糙，反之，则越平滑［6］。将粗糙度引入三维水印，粗糙度较大的区域，表面粗糙，人们对其敏感度降低，嵌入水印后的不可感知性增强。

三维网格模型中三角形数目越多，细节越丰富，粗糙度就越高。同一个面中若面积一定，三角形数目越多，每个三角形所占的面积就越小。因此利用三角形面积的平均值来衡量粗糙度具有实际意义。

1.2 预处理

假设属性信息忽略不计，三维网格模型M能表示为:

M={VN，QN};

VN={0，1，…，N-1}(VN为N 个顶点的集合);

Vi=(xi，yi，zi)表示第i个顶点的坐标信息;

QN表示每个三角面片中与N个顶点拓扑连接关系的集合。

选择候选顶点:

1)根据三维模型的拓扑结构，找出每个顶点的邻接点，剔除顶点数目小于3的顶点。

2)对三维模型的x坐标进行升序排列。

3)计算局部几何空间封闭一环邻域的质心O，使用算法求出所有与该点邻接的点个数之和然后求出与该点所有邻接顶点个数n的比值［7］:

4)计算局部几何空间封闭一环邻域的质心的法向量:

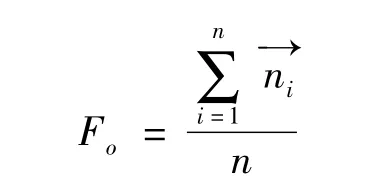
计算局部几何空间封闭一环邻域的质心的加权法向量:

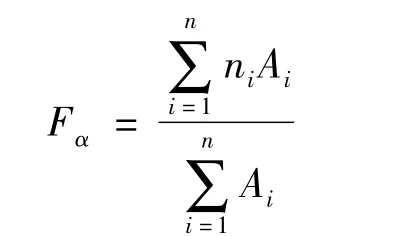
选取2个法向量的夹角小于阈值5的点作为候选顶点。

利用最小包围盒［8］求出中心。将最小包围盒的中心代替模型的中心，避免因修改顶点坐标造成重心偏移。模型各个方向上的的最大值、最小值分别为Xmax、Ymax、Zmax、Xmin、Ymin、Zmin。长方体的中 心 坐 标 是 TBBC

1.3 嵌入算法

利用扩频技术［9］将原始扩展到64位。

根据顶点到中心的距离，可以将顶点分为3N组。

计算所有顶点到中心的距离:

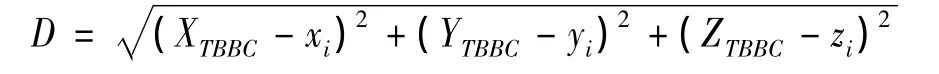
计算最大距离值Dmax和最小距离值Dmin，则分布范围为:

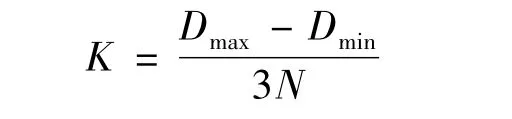
其中N为水印长度。

计算顶点相邻面法向量的夹角的均值作为权值w1。

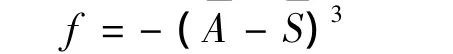
嵌入策略如下:

1)当嵌入水印为+1时，将左右块中粗糙度最大的即权值最大的前k个顶点调整到该块中，从而使权值最大的都落在该块中。调整左边的块，从中选择权值最大的前k个顶点，加上变量，将其调整到该块中。同理，右边的块减去变量，调整到该块中。

2)当嵌入水印为-1时，将该块平分成2块，将2块中粗糙度最大的前k个顶点分别调整到左右两边块里。从该块的左半块内选择权值最大的前k个顶点，减去变量，将其调整到左边的块中。同理，从该块的右半块内选择权值最大的前k个顶点，加上变量，将其调整到右边的块中。

1.4 提取算法

首先计算最小包围盒，求出各个顶点到中心的距离，得到顶点到中心距离的最大值和最小值。

按距离分块，计算每块中顶点个数的总和。如果该块中的个数之和大于左右两块的，水印提取为+1，否则提取为-1。

2 实验结果及分析

实验嵌入水印前后的图像如图1～4所示。肉眼观察到嵌入水印前后图形无明显变化，达到了水印不可见、不可感知的目的。

图1 Dragon嵌入前图像

图2 Dragon嵌入后图像

图3 Bunny嵌入水印前

图4 Bunny嵌入水印后

2.1 鲁棒性

鲁棒性根据三维模型受到攻击后检测出来的水印与原水印的相似度计算。一般使用的评价标准为相似系数corr［10］，指示检测出的水印与原始水印的相似程度。差距越大，corr值越小。

若Q表示原始水印序列，Q'表示提取的水印序列，K表示水印序列的长度，则

在未受到攻击时，检测到嵌入的水印信息值为1。利用QEM简化算法对模型进行30%、50%、70%、90%的简化攻击。Dragon模型和Bunny模型简化结果见表1～2。

表1 Dragon模型简化

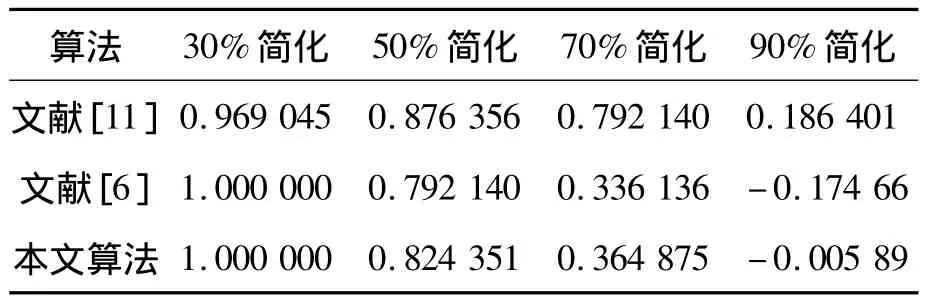
表2 Bunny模型简化

相关系数越大，说明鲁棒性越强。通过和其他文献相比较发现，本算法的鲁棒性得到了提高，具有更大的优势。

分析70%、90%简化时提取失败的原因是简化攻击严重改变了原有模型的细节部分。

表3 0.1%噪声攻击

2.2 不可感知性

不可感知性是三维模型嵌入水印之后，与原三维模型在外观上具有较高的相似性。使用最大均方根距离［12-13］对相似度评估，值越小，相似度越高、不可感知性越强。

若MRMS表示最大均方根距离，M表示原始模型，M'表示嵌入水印后的模型，则:

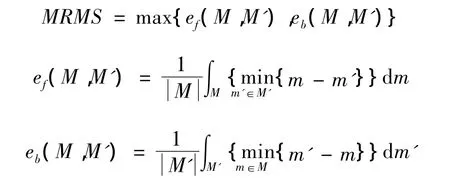
由表4可知，本文算法的最大均方根距离最小，说明模型失真度低，不可感知度强。

表4 最大均方根距离

3 结束语

本文利用一环邻域质心的法向量和加权法向量的夹角来剔除不符合的顶点，选择候选顶点。以最小包围盒的中心作为三维模型的中心，利用点到中心的距离这一几何特征分块，根据粗糙度得到权值，使用顶点相邻面法向量的夹角的均值、顶点邻接三角形的面积均值与所有三角形面积均值的比值作为粗糙度衡量权值，从而选择嵌入顶点。实验结果表明:本文算法能在保证鲁棒性的前提下，降低模型失真度，提高三维模型数字水印的不可感知性，更适合三维模型的版权保护。

［1］Ohbuehi R，Masuda H，Aono M.Watermarking three-dimensional polygonal models［C］//Proceedings of the ACM International Conference on Multimedia’97.Seattle:［s.n.］，1997:261-272.

［2］Guillaume L.A roughness measure for 3D mesh visual masking［C］//Proceedings of the 4th symposium on Applied perception in graphics and visualization.Tubingen，Germany:ACM Press，2007:57-60.

［3］Kami Z，Gotsman C.Spectral compression of mesh geometry［C］//ACM Siggraph 2000.New Orleans，USA:ACM Press，2000:279-286.

［4］喻志强.自适应于局部几何特征的三维模型水印算法［J］.计算机工程与应用，2002(22):23-27.

［5］徐涛.三维网格模型水印自适应调节算法［J］.计算机工程，2012，38(3):113-115.

［6］陈强.基于表面粗糙度的自适应三维模型盲水印算法［J］.计算机应用，2009，29(4):952-955.

［7］冯小青.面向3D网格模型的多重数字水印算法［J］.计算机辅助设计与图形学学报，2010(1):17-23.

［8］邓利平.一种使用几何分布的三维网格模型盲水印算法［Z］.电脑知识与技术，2010.

［9］全红艳.一种基于区域分割的几何模型简化方法［J］.计算机学报，2006，29(10):1834-1842.

［10］唐斌.基于三维网格模型的双重数字盲水印算法［J］.计算机工程，2012，38(6):119-122.

［11］Cho J W，Prost R，Jung H Y.An Oblivious Watermarking for 3D Polygonal Meshes Using Distribution of Vertex Norms［J］.IEEE Transactions on Signal Processing，2007，55(1):142-155.

［12］杨斌.基于表面粗糙度的三维模型质量评价研究［J］.计算机科学，2011，38(1):276-278，285.

［13］姬华民.三维模型数字水印算法研究［D］.济南:山东大学，2011.