钢框架结构正弦扫频振动台试验的虚拟实现*
刘红彪,张 强,刘现鹏,张宝华,田双珠
0 引言
虚拟设计技术是随着计算机技术的发展而产生的新兴技术,被广泛应用于机械制造、航空航天等领域的产品前期规划、设计、试验等各个阶段。由于采用传统工业产品设计方法设计的产品,其结构、功能、操作性能等方面的缺陷往往会在产品开发后期或产品最终试车过程中被发现,进而导致产品需进一步改进设计,导致产品的开发效率低,开发费用增加。采用计算机仿真技术和虚拟实现技术的虚拟设计方法可以大大提高产品的设计效率和质量,提高了产品的市场竞争力(杨志勇,唐胜利,2006)。
正弦扫频试验和随机振动试验是检验产品可靠性,解决各种机械结构振动问题的重要手段,广泛应用于航空航天、汽车以及包装运输等领域,且为结构环境振动试验的核心 (田光明,2005;杨志东等,2008)。在航天产品的研制过程中,正弦扫频试验尤为重要,它是结构模态参数识别的重要手段,产品在正弦扫频下的动力响应结果是重点关注的方面,正弦扫频试验下的结构动力响应结果是反应产品合格与否的重要指标。试验设计的合理性、荷载量级及加载顺序是关系结构正弦扫频振动台试验成败的关键。根据虚拟设计的概念,采用虚拟设计方法对结构正弦扫频振动台试验进行前期的规划、设计、优化,可有效提高试验成功的概率。
本文提出正弦扫频振动台的虚拟设计方法,并精确推导出正弦扫频函数的表示方法,并以此分析正反向正弦扫频试验过程中结构动力反应的差异问题,同时给出环境振动试验中的夹具选择原则,以此建立正弦扫频振动台试验的虚拟设计方法。该研究对指导土木、机械及航空领域产品的正弦扫频试验,合理评估产品在扫频过程中的动力响应均具有参考价值。
1 正弦扫频函数的数学描述
某些抗震试验中 (刘红彪,2012;刘红彪,郭迅,2012;周宝峰等,2013),采用 y(t)=Asin[2πtf(t)],f(t)=2t/4,t∈[0,24]作为正弦扫频函数,似乎可以生成1~64 Hz的正弦扫频函数,其实不然,该函数忽略了函数的频率值是由tf(t)共同决定的,实际生成的扫频信号的频率范围为1~330 Hz。为了获取正弦扫频函数在时域上的精确描述,根据相关理论,进行了如下推导。
一般正弦扫频函数可表述为
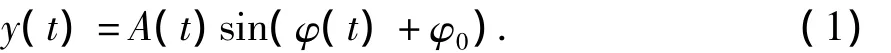
其中:φ0为初相位;设正弦函数随时间变化的频率为f(t),则f(t)=φ'(t)/2π。根据频率变化的规律,频率变化可分为线性变化和对数变化。若正弦扫频函数的频率按照线性变化,则频率变化率可表述为

根据积分可得
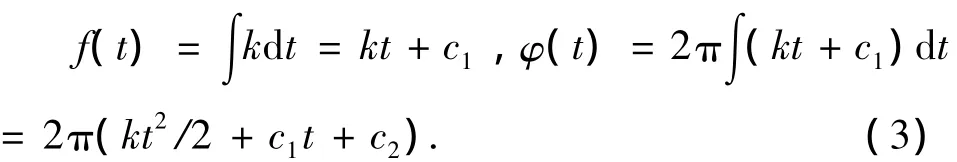
若t=0时的起始频率为f0,t=t1时刻的截止频率为f1,则c1=f0,k=(f1-f0)/(t1-t0);考虑到 c2和φ0可以组成新的初相位,则φ(t)可表示为

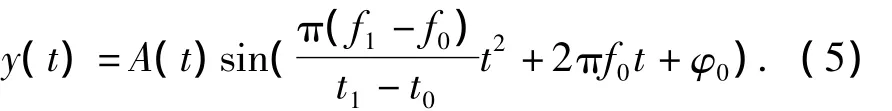
由此,正弦扫频函数y(t)可描述为但线性变化时,频率变化缓慢,达到预期频率花费时间长,一般不采用,试验中常用对数扫频。对数扫频中的频率值可表示为

对 (2)经积分可求得
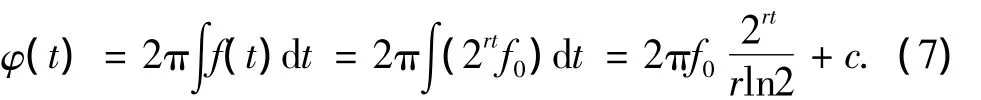
考虑到c和φ0可以组成新的初相位,则φ(t)可表示为

将 (8)式代入 (1)式,则正弦扫频函数y(t)可描述为
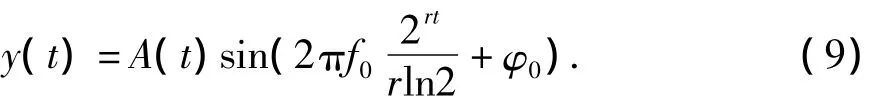
一般在正弦扫频试验时,采用的扫描速率单位为oct/min,且不考虑初相位,故式 (9)可改写为

其中,f0为起始频率,r为扫频速率 (oct/min)。
2 钢框架结构正弦扫振动台试验的仿真分析
机械领域的结构环境振动试验属于高频范畴,由于被测试件的结构固有频率较高,电磁振动台的台面作为独立结构件与试验件耦合,其动力特性对试验件的动力响应有一定影响。但一般民用建筑结构的固有频率较低 (低于50 Hz),属于低频范畴(刘红彪等,2011a,b),振动台台面的固有频率一般为试件固有频率的3倍以上,台面的耦合作用对试件动力响应的影响可以忽略,故在民用建筑正弦扫频振动台试验中不分析台面耦合效应。
2.1 典型试件概况
随着经济的发展和人工成本的增加,钢结构由于自重轻、工业加工自动化程度高、结构抗震性能优越等特点被广泛应用于超高层建筑、大跨空间结构等领域 (何敏娟等,2010;黄思凝等,2012)。为了设计五层钢框架结构的正弦扫频振动台试验,先进行该结构的虚拟设计。该五层钢框架的长和宽分别为800 mm和600 mm,一、二层层高为450 mm,三至五层层高均为390 mm,各层楼板为厚度25 mm的钢板。模型的立面图、细部图和现场照片图如图1所示。
为了了解钢框架结构的动力特征,分别进行了结构的模态仿真分析和模态测试试验。模态测试试验设备采用941B测振仪的加速度档,灵敏度为3.10 V/g;试验中使用初速度法对模型实施激励,可以激起模型结构的高阶振动 (刘红彪等,2011a,b)。通过数据采集器获取结构振动的时域数据,采用频域分析方法对时域数据处理分析获取了结构横向的五阶固有频率 (表1)。根据该五层钢框架的相关参数,采用Abaqus有限元建模计算,获取了钢框架结构的模态信息,其中,钢框架结构的横向的五阶固有频率值详见表1,结构的前五阶振型如图2所示。通过实测数据和数值模拟结果对比可知,数值计算的固有频率值与实测结果较接近,由此证明该有限元模型是合理的,该模型为后续结构的正弦扫频振动台的虚拟实现奠定了良好的基础。

图1 模型立面图 (a)、细部图 (b)和现场照片 (c)Fig.1 Elevation(a),angle iron details(b)and locale photo(c)of the model

图2 模型结构的模态(a)模型;(b)一阶;(c)二阶;(d)三阶;(e)四阶;(f)五阶Fig.2 Modal of model structure(a)model;(b)first order;(c)second order;(d)thind arder;(e)forth order;(f)fifth order
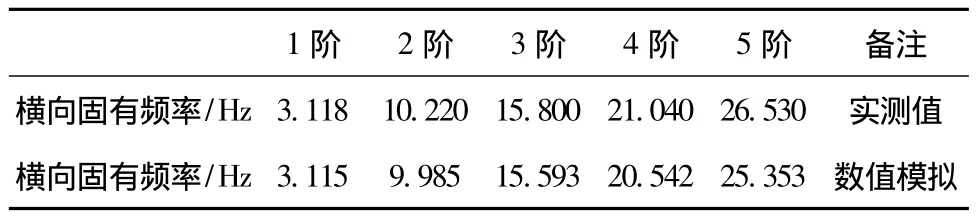
表1 结构横向的固有频率值Tab.1 Natural frequencies of model structucre in transverse
2.2 结构的正弦扫频仿真分析
正弦扫频试验是检验产品可靠性,解决各种结构振动问题的重要手段,尤其是在航空产品的研制过程中,正弦扫频试验相对于随机振动试验、冲击试验、离心加速度试验是最能反映产品可靠性的技术指标。在土木工程领域中,正弦扫频试验一般用于结构的模态参数识别,尤其对结构的阻尼比测量较为有效。虚拟实现结构的正弦扫频振动台试验对了解结构的动力特性,指导实际试验合理选择地震波的类型及量级均具有重要意义。
根据五层钢框架结构的动力特征,在台面底部输入1~32 Hz的正弦扫频激励,设定结构的各阶阻尼比为5%,通过Abaqus有限元软件采用振型叠加法进行组合体结构的动力时程反应分析计算。正弦扫频激励持时 60 s,扫描速率为5.0 oct/min,分为正向和反向分别输入计算分析,其中正向输入的正弦扫频时程曲线及其傅里叶谱详见图3,频率随时间变化的曲线如图3c所示。
正弦扫频激励的最大峰值加速度为1.0 g,经过有限元建模计算获取了钢框架结构的动力响应,其中正向和反向扫频时结构的动力响应曲线详见图4。从曲线上看,正反向扫频时结构的反应趋势是一致的,结构的最大反应发生在一阶固有频率处,最大加速度发生在结构的五层,和相关理论相符合。
为了对比正反向扫频对结构动力响应的影响,取结构第五层的响应结果进行对比 (图5)。经比对可知,正向正弦扫频时,试件的最大反应发生在3.385 Hz处,五层的最大反应的加速度值为11.12 g(图5a),放大倍数为11.12;反向扫频时最大反应发生在2.920 Hz处,五层的最大反应加速度值为10.23 g(图5b),放大倍数为10.23。可见正反向正弦扫频时,试件的最大反应发生的频率值存在一定差异,但差异很小,这种情况在实际的正弦扫频振动台试验时也同样存在,但对试验的结果影响不大;同时,根据结构的放大倍数为2倍阻尼比的倒数可知,结构的放大倍数结果是合理的。
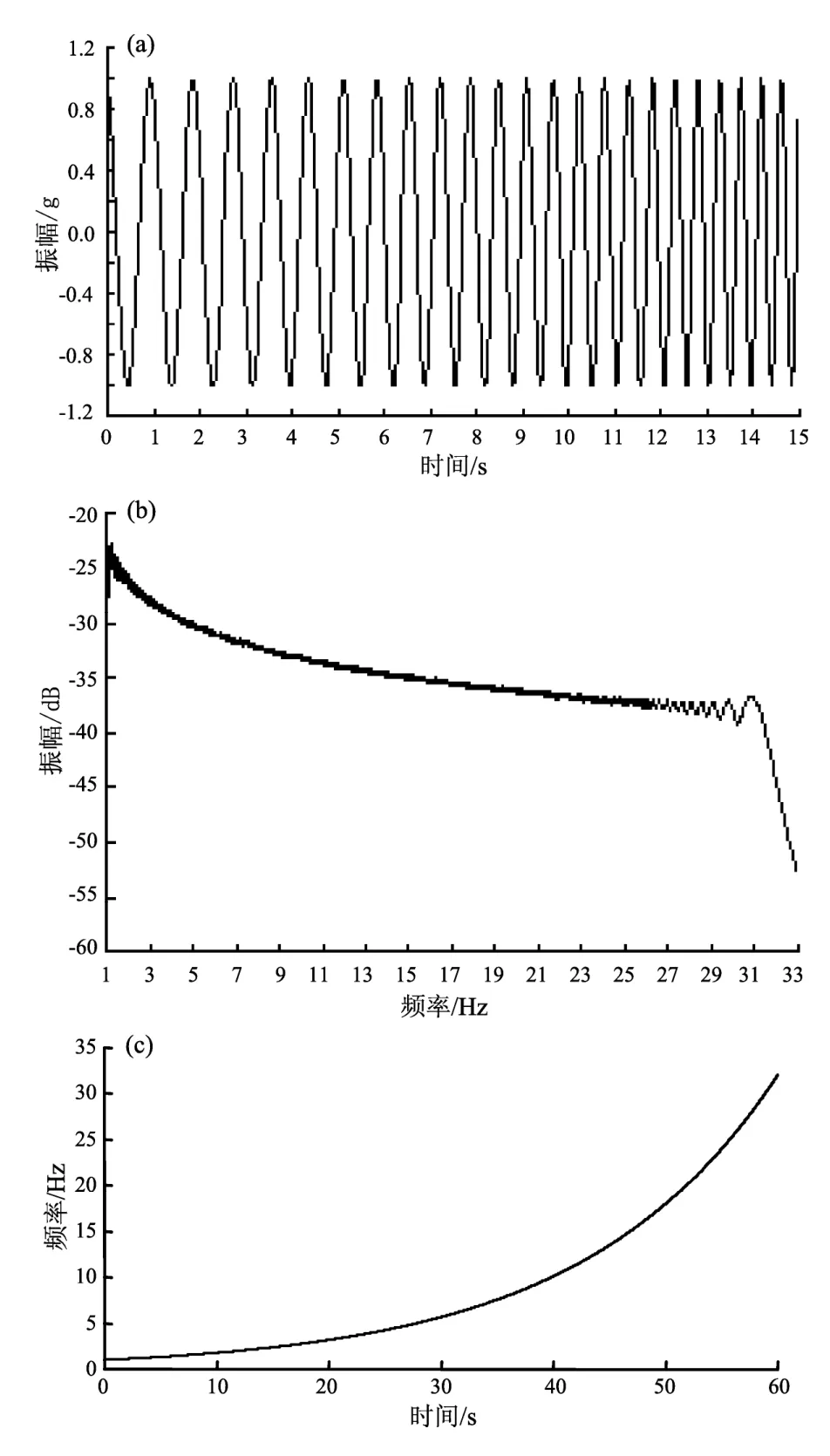
图3 正弦扫频曲线及其傅里叶谱(a)时程曲线;(b)傅里叶谱;(c)频率变化曲线Fig.3 Sine sweep vibration curve and its Fourier spectrum(a)time history curve;(b)Fourier spectrum;(c)frequency varying curve

图4 正弦扫频下的结构动力响应(a)结构动力响应时程曲线 (正向扫频);(b)结构动力响应频域曲线 (正向扫频);(c)结构动力响应时程曲线(反向扫频);(d)结构动力响应频域曲线 (反向扫频)Fig.4 Structural dynamic response excited by sine sweep vibration(a)time history curve of structural dynamic response(forward sweep);(b)structural dynamic response curve in frequency domain(forward sweep);(c)time history curve of structural dynamic response(reverse sweep);(d)structural dynamic response curve in frequency domain(reverse sweep)

图5 正反向正弦扫频下的结构动力响应对比(a)结构动力反应曲线;(b)局部曲线Fig.5 Comparision of structural dynamic response excited by forward and reverse sine sweep vibration(a)structural dynamic response curve in frequency domain;(b)local curve
3 结论
本文通过正弦扫频函数的理论推导和典型钢框架结构在正弦扫频激励下的时程计算分析,得到如下结论:
(1)通过理论推导,获得了正弦扫频函数的精确描述,可为土木、机械及航空领域结构的正弦扫频振动台试验的设计及动力时程数值仿真提供理论依据。
(2)结构正弦扫频振动台试验时,应根据振动台面的动力特性确定是否考虑振动台的耦合作用对试验件动力响应的影响;根据仿真分析可知,结构在正反向正弦扫频激励下的动力响应存在频率点上的微小差异,但差异不大,两个方向上的动力结果均可作为试件力学性能的评定指标;同时,采用振型叠加法的动力时程分析方法计算结构在正弦扫频激励下的动力响应是可行的,且计算速度较快。
何敏娟,梁峰,马人乐.2010.大型超高钢结构电视塔模拟地震振动台试验研究[J].振动与冲击,29(1):77-80.
黄思凝,郭迅,刘红彪.2012.高层钢筋混凝土斜交网格结构振动台试验研究[J].振动与冲击,31(11):127-132.
刘红彪,郭迅,李国东.2011a.乐音准则法及其在结构损伤诊断中的应用研究[J].振动与冲击,30(10):254-259.
刘红彪,郭迅,梁永朵,等.2011b.9度设防区房屋结构自振周期测试[J].建筑结构,41(5):60 -62.
刘红彪,郭迅.2012.极震区典型砌体结构的振动台倒塌对比试验分析[J].土木工程学报,31(6):18-28.
刘红彪.2012.底商多层砌体结构倒塌机理研究[D].哈尔滨:中国地震局工程力学研究所.
田光明.2005.正弦扫描振动响应的时频分析[J].振动与冲击,24(6):13-16.
杨志东,丛大成,韩俊伟,等.2008.基于扩展型准牛顿优化算法的单轴正弦扫频控制[J].振动与冲击,27(3):99-103.
杨志勇,唐胜利.2006.汽轮机扭叶片的虚拟设计[J].重庆大学学报(自然科学版),29(1):26-29.
周宝峰,于海英,温瑞智,等.2013.一种识别永久位移的新方法[J].土木工程学报,46(增刊2):135-140.

