三维任意各向异性介质中海洋可控源电磁法正演研究

殷长春，贲放，刘云鹤，黄威，蔡晶

吉林大学地球探测科学与技术学院，长春 130026

1 引言

海洋可控源电磁法（Marine Controlled－Source Electromagnetic，简称MCSEM）是近年大力发展并被逐渐广泛采用的海洋地球物理勘查技术.作为海洋地震的辅助手段，海洋电磁勘探可以有效地进行储层评估.Cox（1980）提出了采用水平电偶源的海洋可控源电磁法进行海底地质情况调查；Chave等（1982）对海洋电磁一维频率域正演算法做了深入研究；Edwards等（1986，1997）对偶极－偶极装置海洋可控源电磁法做出理论研究；而Sinha等（1990）研究了可以进行海洋电磁测深的可控源电磁法仪器，并且进行了系列实验.Constable等（1996）通过做PEGASUS实验认识到海洋可控源电磁法在海底测深方面有明显的效果；Hoversten等（1998）的研究得出结论：结合海洋地震和海洋电磁技术可以提高海洋油气勘探的精度.自2002年Eidesmo等提出SBL（Sea Bed Logging）勘查技术，海洋可控源电磁法在理论和应用方面迅速发展.Constable（2007）对MCSEM在油气勘探开发中的应用做了系统的阐述，指出了MCSEM的优势以及需要改进的技术性问题；Um等（2007）通过电流切面的分布特征分析海底电流场扩散方式；Constable（2010）对从2000—2010年的海洋可控源电磁法的发展作出系统总结，探讨了海洋可控源电磁法的重要性及未来发展趋势；Crepaldi等（2011）利用解析导数的方法进行了共中心点海洋电磁数据快速反演；刘云鹤等（2012）利用欧拉旋转分析了由于洋流等因素产生的发射源姿态的改变对海洋可控源电磁法数据解释的影响.

海洋可控源电磁数据三维正、反演技术于本世纪初逐渐趋于成熟，并且已应用到实际生产中.Zhdanov等（2006）分析了积分方程法在三维电磁模拟中的优势并应用到MCSEM三维模拟中，取得了非常好的效果；Gribenko等（2007）利用积分方程和正则化Zhdanov（2002）聚焦技术对三维MCSEM进行反演，有利于对海底油气储层的圈定；Commer等（2008）研究了基于混合模型的三维海洋可控源电磁法反演加速方法；杨波等（2012）利用有限体积法研究了考虑海底地形的三维频率域可控源电磁模拟，分析了海底地形对MCSEM电场分量的影响；Sasaki（2013）利用有限差分法进行海洋电磁三维正演并利用高斯牛顿法进行反演，给出了海洋可控源电磁法对浅海海底高阻薄层的三维反演结果.

由于海洋可控源电磁响应受海底介质的各向异性影响很大，电各向异性对海洋电磁数据的影响成为海洋电磁法的研究热点.Everett等 （1999）对各向异性海底介质的一维MCSEM响应进行了研究，Yin（2006）给出了层状任意各向异性介质中的海洋大地电磁一维正演算法，Løseth等（2007）对一维海洋可控源任意各向异性算法进行深入研究，分析了不同各向异性条件下的海洋可控源电磁响应特征，Kong等（2008）对2.5维水平各向异性海洋可控源电磁法有限元正演算法进行了研究，陈桂波等（2009）利用三维积分方程法研究了海底TI地层中MCSEM电磁响应特征，Newman等（2010）利用非线性共轭梯度法实现了TI介质中的三维海洋可控源电磁法反演，并成功应用到实测数据处理中，Li等（2011）研究了TI介质二维倾斜各向异性的有限元正演算法，并研究了二维情况下倾斜各向异性的影响规律.

到目前为止，电各向异性及对海洋电磁相应影响特征的研究均主要针对一、二维及简单的三维TI介质模型.而国际最大的几家海洋电磁技术服务公司已开始向客户提供海洋可控源三维电磁各向异性资料解释服务.本文研究任意各向异性介质中（电导率张量为任意3×3对称正定矩阵）三维海洋可控源电磁响应的正演模拟算法，利用交错网格三维有限差分技术求解散射电场的耦合微分方程.对于与电场同向的电流密度分量，各向异性电导率张量通过体积加权平均进行离散，而对于电流密度和电场不同向的情况，电导率张量利用空间电流密度加权平均.为实现集成方程的有效求解，我们采用拟最小残差法（Pre－Conditioned Quasi－Minimal Residual QMR），通过对比各项同性和各向异性导电介质中存在高阻储油层时海洋可控源电磁响应，分析各向异性对目标体响应的影响特征及高阻储油层设别技术.

2 正演理论

假设时谐因子为eiωt，其中任意各向异性地层中的二次散射场偏微分方程为（Weiss et al.，2006）

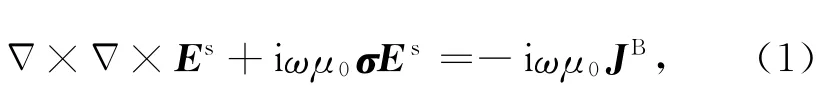
式中μ0为磁导率，取为自由空间中的磁导率值μ0＝4π×10－7H／m，Es为二次散射电场，JB为源项

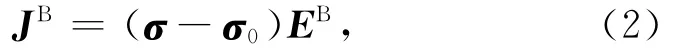
方程（1）和（2）中的一次电场EB利用全空间格林函数求取.σ和σ0为3×3的对称正定电导率张量.为方便计算，σ0通常假设为均匀半空间模型或者水平层状模型.任意各向异性介质中的电导率张量可表示为

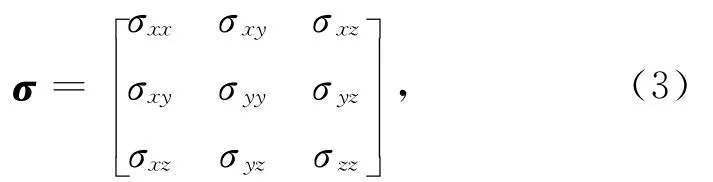
x，y，z表示直角坐标系三个坐标方向.（3）式中的对角和非对角元素将各向异性介质中不同方向的电场和电流密度耦合在一起.为得到任意各向异性介质的电导率张量σ，通常先设定一个参考电导率张量σc（其三个主对角元素分别对应电各向异性的三个主轴），即

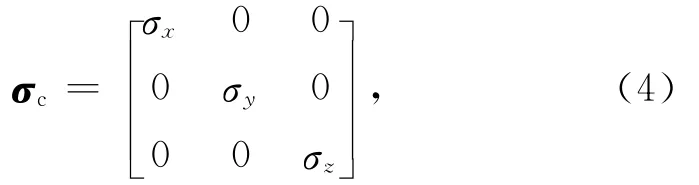
再通过三重欧拉旋转即可得到任意各向异性介质的电导率σ（图1）：

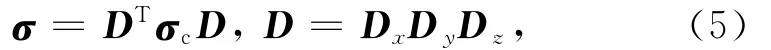
其中旋转矩阵为

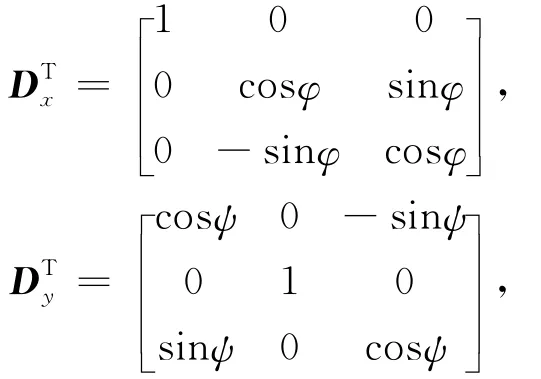
利用有限差分技术进行数值模拟（Newman et al.，1995），需将方程（1）分解为x，y，z三个方向的标量方程：

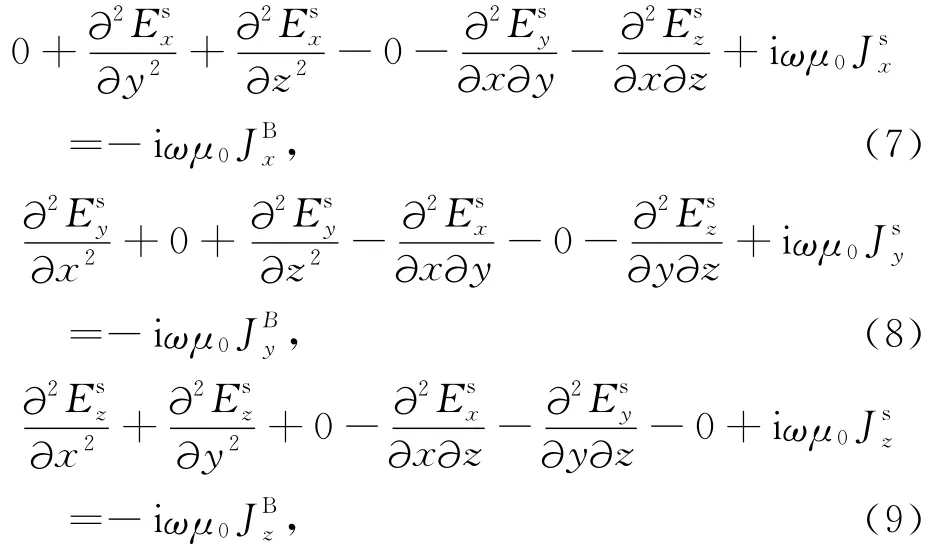
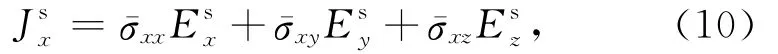
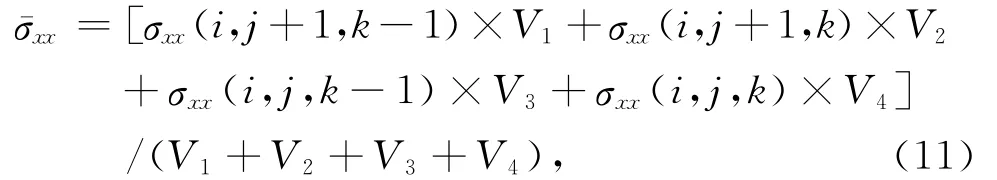
其中V1，V2，V3，V4为电导率对应电场分量所属网格体积的1／4.

对于式（10）中右端后两项，由于电场与电流密度方向不同，我们采用空间电流密度平均技术将电场耦合到电流密度计算点上，即

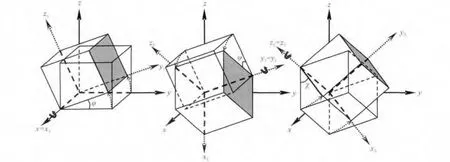
图1 坐标旋转示意图（Gellert et al.，1986）Fig.1 Rotation of the coordinate system （Gellertet al.，1986）

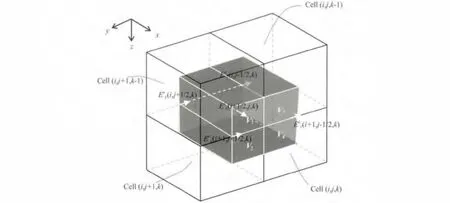
图2 任意各向异性介质中电导率近似方法Fig.2 Approximation of the conductivity tensor elements for an arbitrarily anisotropic earth

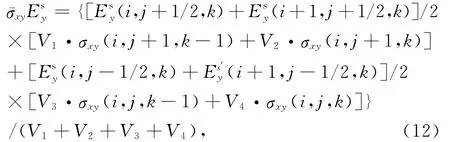
采取相同的方式进行离散.对（7）—（9）式离散化之后，可得到如下矩阵方程

式中A为大型复稀疏对称矩阵，e为待求二次电场向量，b是方程（1）的右端源项.我们利用拟最小残差法QMR（Freund，1993）求解方程组（13）.

3 数值计算结果

3.1 精度验证

本文利用Løseth和 Ursin（2007）的一维倾斜各向异性模型结果对本文算法进行精度验证.模型设计如图3，海水层厚300m，电导率σ＝3.2S·m－1；海底覆盖层厚1000m，电导率σ＝1.0S·m－1；异常高阻层厚度100m，取参考电导率张量元素为σxx＝0.01S·m－1，σyy＝0.01S·m－1，σzz＝0.025S·m－1，并令参考电导率张量绕y轴旋转30°；高阻异常层下面是电导率为σ＝1.0S·m－1的均匀半空间.发射源为沿x方向的水平单位电偶源，发射频率0.25Hz，发射电流1A.利用本文有限差分计算的Ex响应结果与Løseth和Ursin（2007）一维半解析结果对比如图4所示.从图可看出两种方法计算结果吻合非常好，最大相对误差不超过1.7%，大收发距时误差均小于0.5%，说明本文算法具有较高精度.

图3 精度验证模型Fig.3 Model for checking the modeling accuracy

3.2 海底各向异性对海洋可控源电磁响应的影响特征

为了分析海底介质各向异性对海洋可控源电磁响应的影响特征，我们建立如图5所示的三维地电模型，其中海底半空间为各向异性，三维高阻异常体为各向同性.海水的深度为1000m，电导率为3.33S·m－1.高阻异常体顶部埋深为1000m，中心在海底投影点的空间坐标为（5000m，0m，1000m），大小为6000m×6000m×100m.发射机为沿x方向的水平电偶源，发射频率0.25Hz，发射电流1A，距海底30m.三维模型剖分为108×108×56个单元，其中包括每个边向外扩的四个格（2倍扩边），剖分单元长、宽、高分别为200m、200m、100m.为了更精确地得到三维高阻异常体的响应，在其所在位置z方向网格长度细分为25m.本文的正演模拟是在Intel®CoreTMi7－4770CPU ＠3.40GHz，8GB DDR3 1600MHz内存，NVIDIA GeForce GTX 650显卡的PC的环境下进行，一次正演需要的时间大约11min.

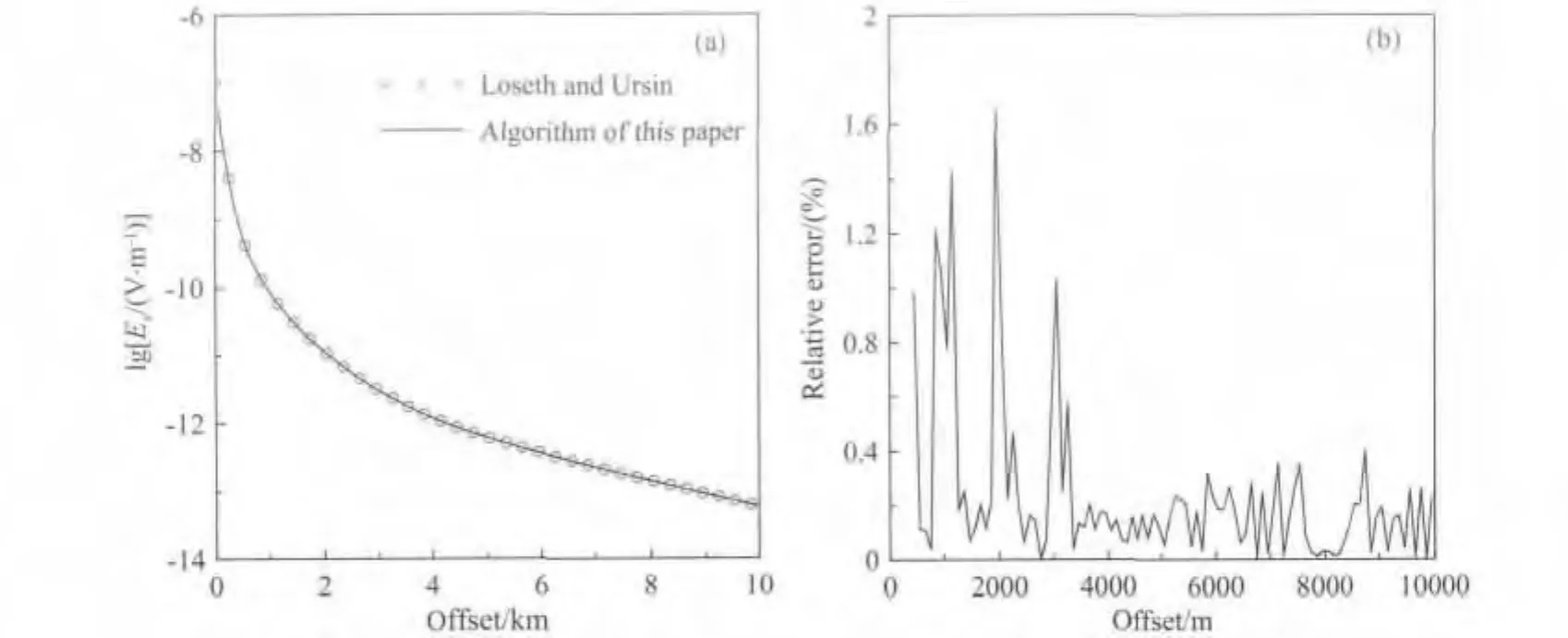
图4 验证结果与误差分析Fig.4 Modeling accuracy check and error analysis

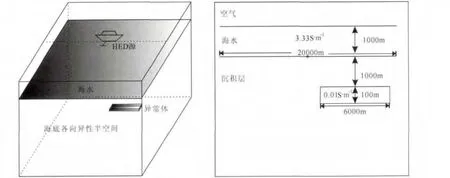
图5 海洋电磁三维各向异性模型Fig.5 Marine 3Danisotropic model

下面首先讨论海底各向异性半空间电导率沿x方向变化的情况；进而通过对参考电导率张量分别绕y和z轴旋转45°得到倾斜各向异性的电导率参数，研究倾斜各向异性对海洋可控源电磁响应的影响特征.设海底半空间参考电导率张量为

我们分别讨论两种情况：（1）没有旋转，只改变x方向的主轴电导率；（2）针对4种不同的参考电导率张量，分别绕y和z轴旋转45°.当参考电导率张量的对角线元素相同时（相当于各项同性），欧拉旋转不影响电导率分布，由此我们只需研究10种各向异性电导率模型组合情况.我们以各向同性模型作为参考，分别研究同线Ex分量的振幅MVO和相位PVO曲线，电场分量Ex，y，z的平面分布特征，以及xz、xy切面的电流分布特征，讨论不同各向异性情况对海洋可控源电磁响应影响规律.

3.2.1 各向同性海底介质的电磁场分量特征

为方便对比，首先考虑围岩为各向同性情况.令围岩电导率为σ＝diag（1.0，1.0，1.0），计算出电场三分量振幅分布如图6.由于高阻异常体位于模型中心的右方，三个电场分量的振幅分布均非中心对称.无论在xy平面还是在纵向断面图上，电场各分量和电流密度在高阻体附近均呈现出较为明显的延展趋势.图7为各向同性情况下xy和xz切面的电场和电流分布.由图可见：（1）在发射源附近，电场和电流均展示水平电偶极子场的分布特征；（2）海底上下两侧的在xy切面上可明显看出由高阻异常体引起的场分布向右延展；（3）由于和围岩电导率存在巨大差异，高阻异常体中的电流密度近于直立.这是由于电场水平分量连续，所以高阻体中几乎不存在水平电流，而垂向电流密度在穿透高阻层时始终保持连续的结果；（4）在收发据很大的情况下，电流分布呈现水平，电磁场中空气波占主导地位（殷长春等，2012）.

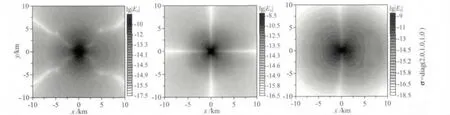
图6 海底各向同性介质表面的电场分布Fig.6 Plane view of electrical field at the surface of an isotropic half－space under the ocean

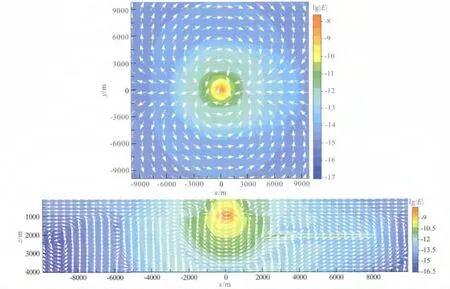
图7 海底各向同性介质中的电场及电流分布（等值线表示电场分布，箭头表示电流方向）Fig.7 Distribution of electrical field and current in an isotropic half－space under the ocean（The contour denotes the electrical field，while the arrows show the current）

3.2.2 海底围岩x方向电导率对电场和电流分布特征的影响

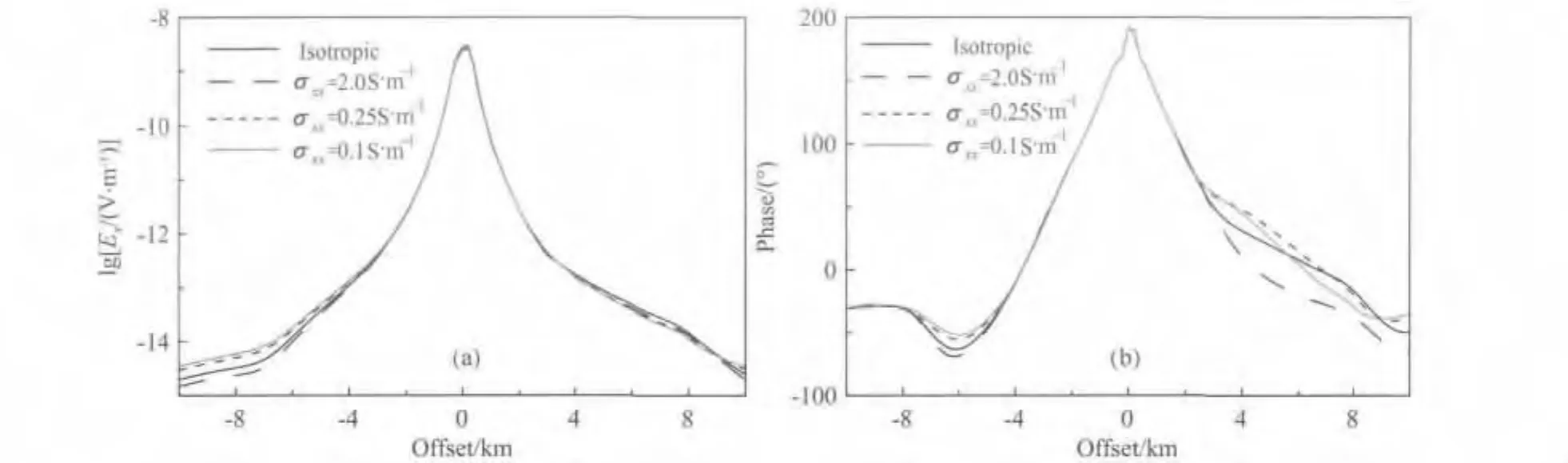
图8 海底介质x方向参考电导率变化对Ex分量振幅和相位的影响Fig.8 Influence of the reference conductivity in x－direction on the amplitude and phase of Ex

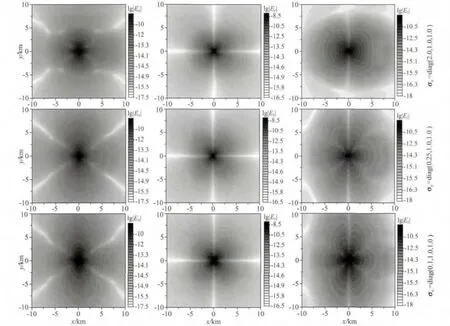
图9 海底介质x方向参考电导率变化对电场分布特征的影响Fig.9 Influence of the reference conductivity in x－direction on the distribution of E－field

当海底介质中只有x方向电导率发生变化时，同线Ex分量的振幅和相位曲线均发生不同程度的改变（图8）.由于良导和高阻介质中电磁波衰减速度不同，振幅曲线左支（远离高阻层）呈现与电导率反向变化特征.相位曲线左支变化也体现明显规律性.由于高阻异常体的存在，右端曲线变化比较复杂.中间小极距区由于直达波占主导地位，仅与海水导电率有关，受海底介质影响很小，因此不能反映海底介质的电性变化特征.图8中右侧由于高阻体的存在，电磁响应受高阻层中导波的影响，造成振幅与相位曲线右支变化没有明显的规律性.从图9和10电场分布的xy切面可以看出，随着x方向电导率的减小，电场Ex平面分布沿y方向发生明显延展，说明电导率沿x方向变化对旁线测量的电场产生较大影响.相比之下，电场Ey受海底介质的x方向的电导率影响较小.由图10可进一步看出：（1）随着海底介质x方向电导率的减小，发射电流受到挤压而流向垂直方向；（2）xz平面内电流方向在x方向电导率为2.0s·m－1时向x方向偏，特别是在高阻储层的上下，基本沿水平方向流动，说明此时电流试图水平绕过高阻体.对于x方向电导率为0.25s·m－1和0.1s·m－1的情况，z方向电导率与之相比为高导，所以此时海底沉积层中的电流偏向垂向方向.随着x方向电导率减小，电流由水平环绕、倾斜穿入到垂直穿透高阻层；（3）如前所述，由于高阻储层和围岩电导率巨大差异，高阻储层内的电流方向基本为垂向方向；（4）与垂直切面情况相比，水平方向电流分布变化较小.发射源两侧的水平电流形成的电流环根据x方向电导率的变化呈现不同程度的向y方向延展.

3.2.3 海底介质电导率绕y轴旋转45°电场和电流分布特征

当海底介质参考电导率张量绕y轴旋转时，电场三个分量均发生剧烈变化.图11和12给出上述4种不同参考电导率张量绕y轴旋转45°的计算结果.由图可以看出，同线Ex分量左右支变化规律一致，良导情况下电磁响应弱，而高阻情况下电磁响应强；由于电导率张量旋转导致电场各分量的平面分布特征发生变化.从图13中的电流与电场分布可以看出，当参考电导率张量绕y轴旋转时，xz切面内电流方向发生明显变化.当x方向参考电导率比z方向低时，绕y轴旋转后的电流及电场分布向右侧偏，说明此时电磁能量主要向右侧良导方向传播，而高阻储层正好位于模型右侧，所以最终在海底测点位置的电场响应较大；而当x方向参考电导率为比z方向参考电导率高时，绕y轴旋转后的电流方向及电场分布偏向远离高阻储层的左侧方向，造成海底测点位置的电磁响应较小.从图13也可以看出与图12类似的特征，当x方向的电导率较高时，电流基本绕过高阻异常体；而随着x方向电导率的降低，由电导率旋转引起的电流穿过高阻体构成倾斜电流通道.

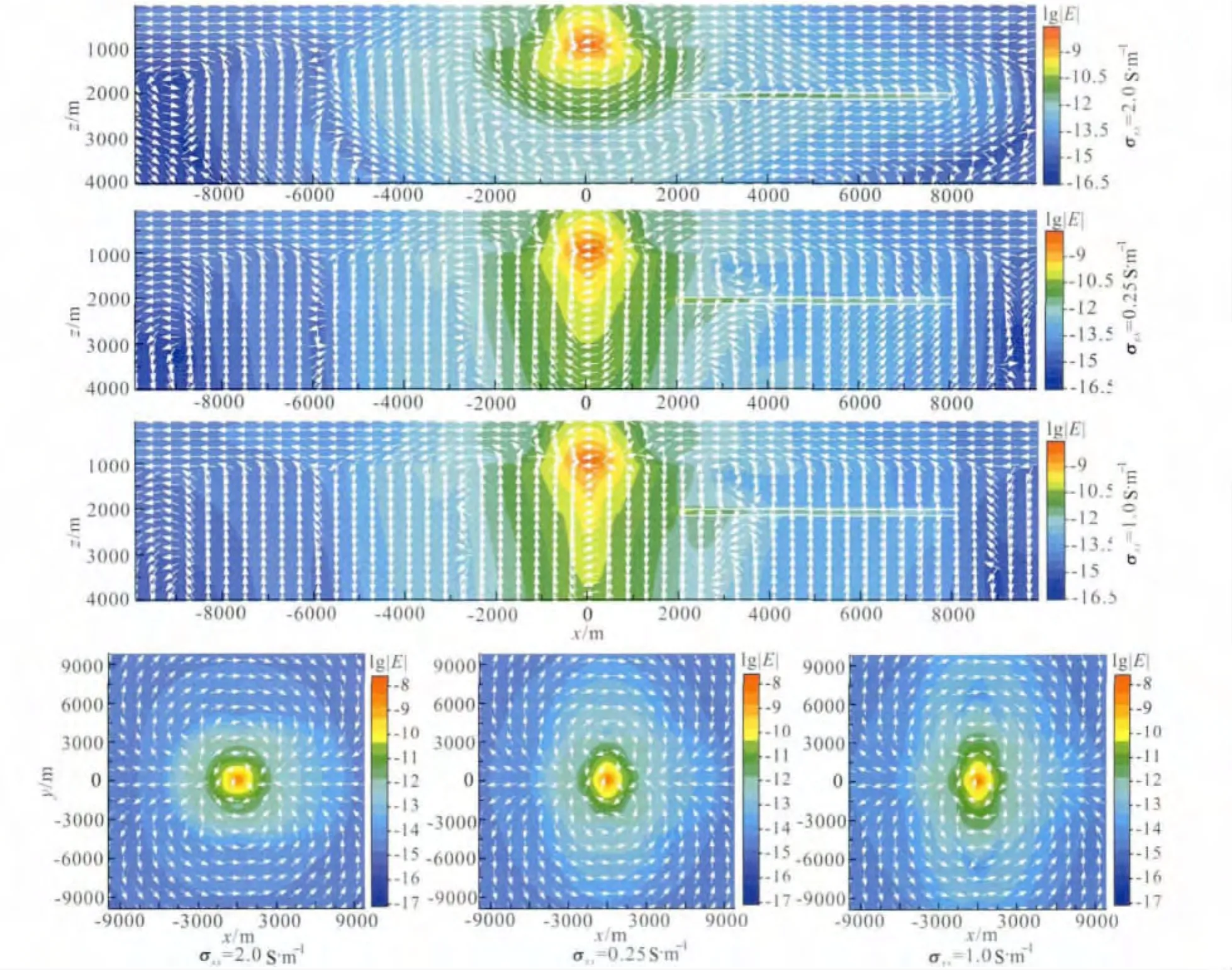
图10 海底介质x方向参考电导率对电场和电流分布特征的影响Fig.10 Influence of the reference conductivity in x－direction on the distribution of E－field and the current

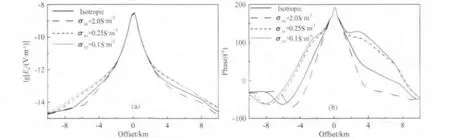
图11 参考电导率张量绕y轴旋转45°同线Ex分量振幅和相位曲线Fig.11 Amplitude and phase of Exfor reference conductivity tensor rotated around y－axis at 45°

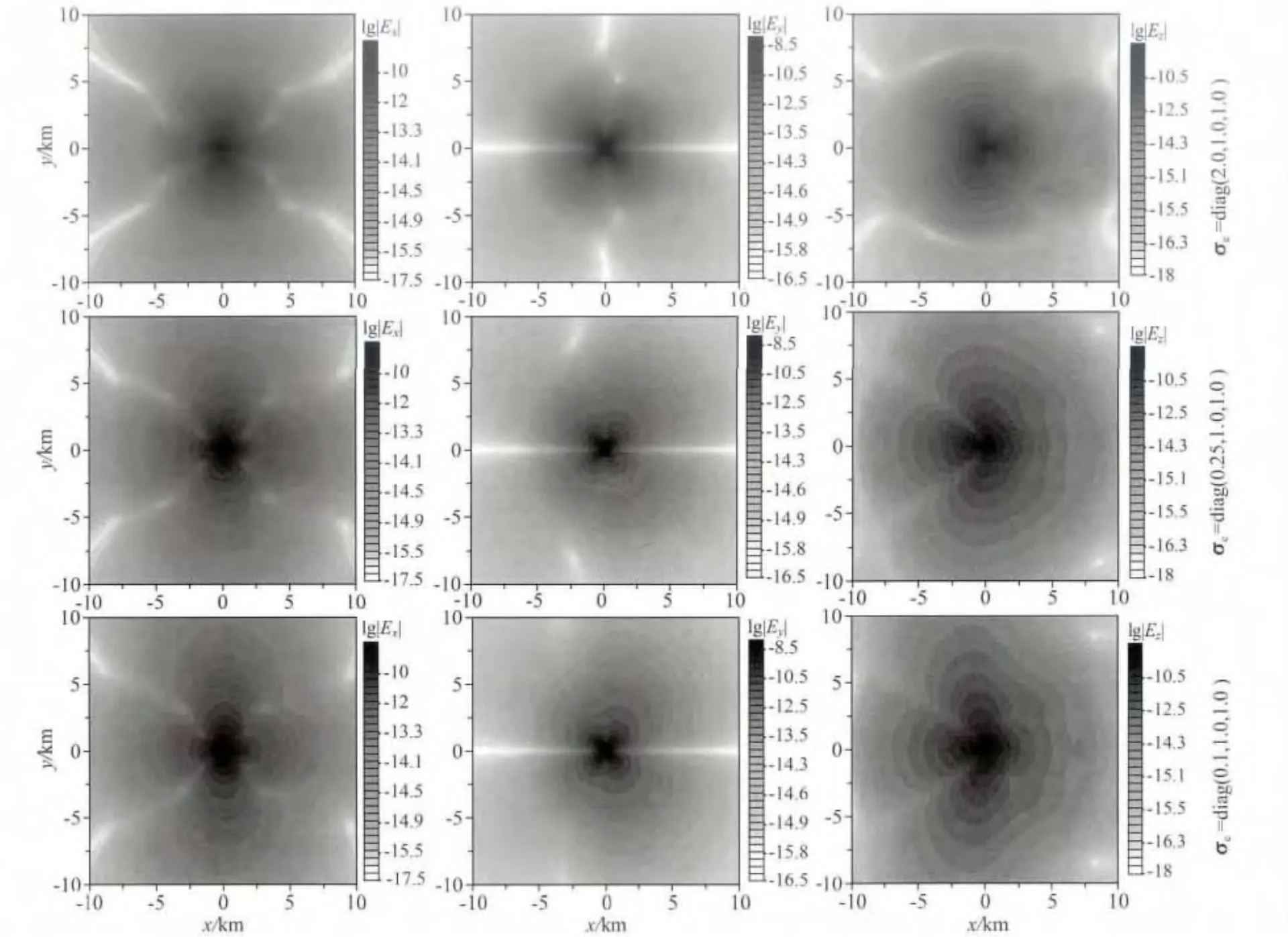
图12 参考电导率张量绕y轴旋转45°时电场分布Fig.12 Plane view of electrical field for reference conductivity tensor rotated around y－axis at 45°

3.2.4 海底介质电导率绕z轴旋转45°电场和电流分布特征

当海底各向异性介质的参考电导率张量绕z轴旋转时，电磁能量的传播特征变化主要发生在xy平面内，由此较之于电导率张量没有发生旋转的情况（图9），电场三个分量的平面分布均发生较明显绕z轴转动特征（如图15），易于识别海底介质的各向异性特征.由于旋转后x方向电导率差异变小，4种各向异性情况下同线Ex电场分量的振幅和相位曲线左支差异相应变小.对于振幅与相位曲线右支而言，由于高阻储层的存在，4种各向异性情况的响应差异仍然比较明显.由图15可以看出，电场分布明显反应海底介质的各向异性特征，有助于识别海底各向异性特征和分布规律；而从图16可以看出，相对于没有发生旋转时电流随着x方向电导率的减小由环绕到直接穿透的情况（图10），当海底介质电导率张量绕z轴旋转时，垂直切面内高阻储层上下电流均沿倾斜方向，倾斜穿透高阻层.

4 结论

本文基于有限差分法并结合空间电流密度平均技术提出了一种任意各向异性情况下三维海洋可控源电磁正演模拟算法.通过与一维层状任意各向异性介质的电磁响应对比验证了该算法的精度和有效性.通过对各种各向异性条件下海洋可控源电磁Ex响应MVO和PVO曲线特征、电场三分量平面分布及水平和垂向切面内电流和电场分布特征的研究，海底地层各向异性对MCSEM响应的影响规律可系统总结如下：

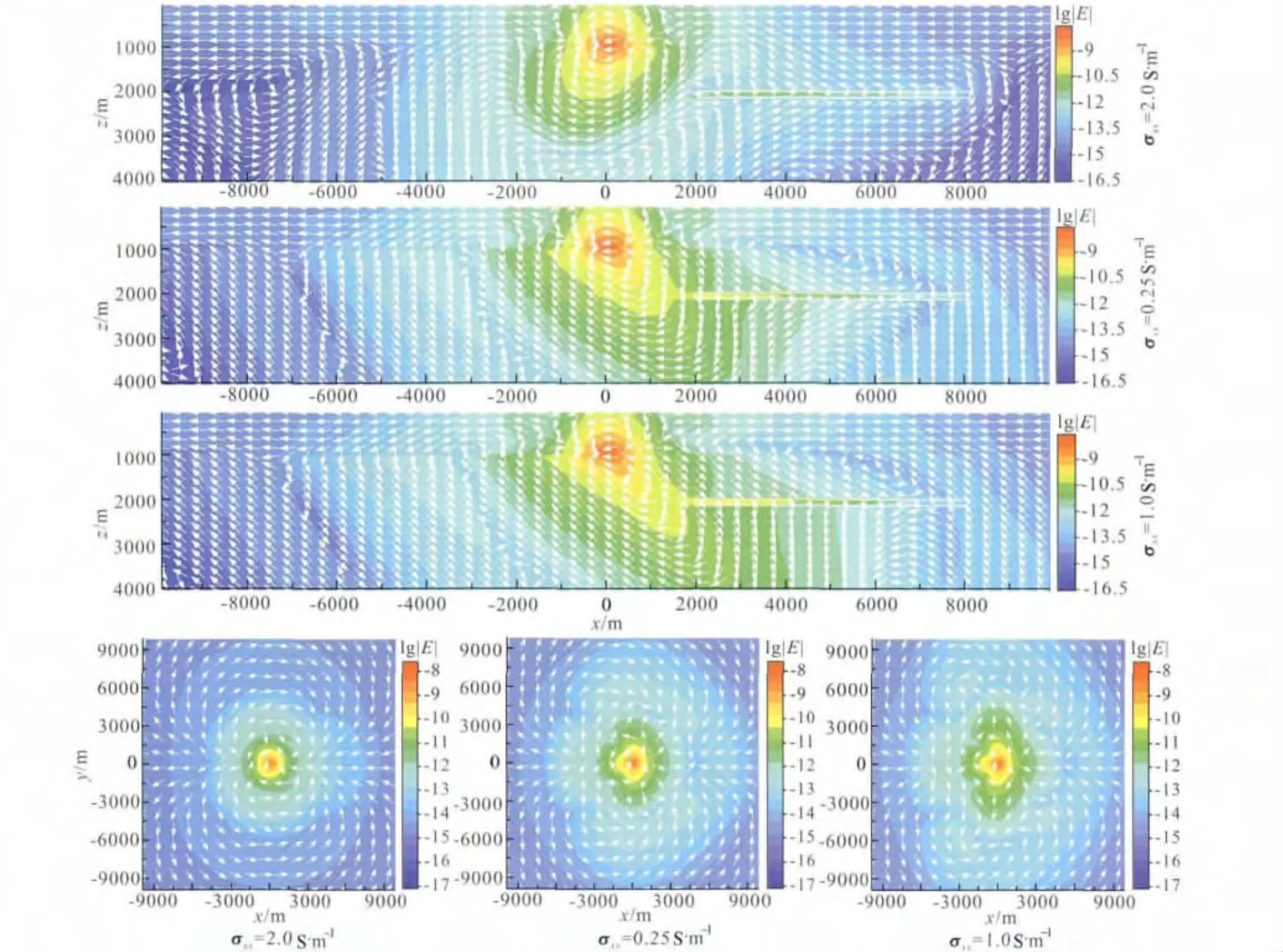
图13 参考电导率张量绕y轴旋转45°时电场和电流分布Fig.13 Distribution of the electrical field and current for reference conductivity tensor rotated around y－axis at 45°

图14 参考电导率张量绕z轴旋转45°同线Ex分量振幅和相位曲线Fig.14 Amplitudes and phases of Exfor reference conductivity tensor rotated around z－axis at 45°

（1）当海底介质为各项同性时，随着主轴x方向电导率的降低，电流由水平绕过，到垂直穿过高阻板状异常体；电场在海底的分布受高阻体影响发生水平拓展，因而据此可判断高阻体的存在.

（2）由于和围岩的巨大电阻率差异，高阻异常体中的电流几乎垂直高阻体的层界面.

（3）由于各向异性介质中的通道（channeling）效应，电流明显向导电介质的层理方向聚焦，导致高阻体激发被加强，电场和电流密度异常特征明显.

（4）从海洋电磁的MVO和PVO曲线可以明显看出，高阻异常体一侧的曲线变化幅度大，说明异常体的响应受海底介质的各向异性影响较大.

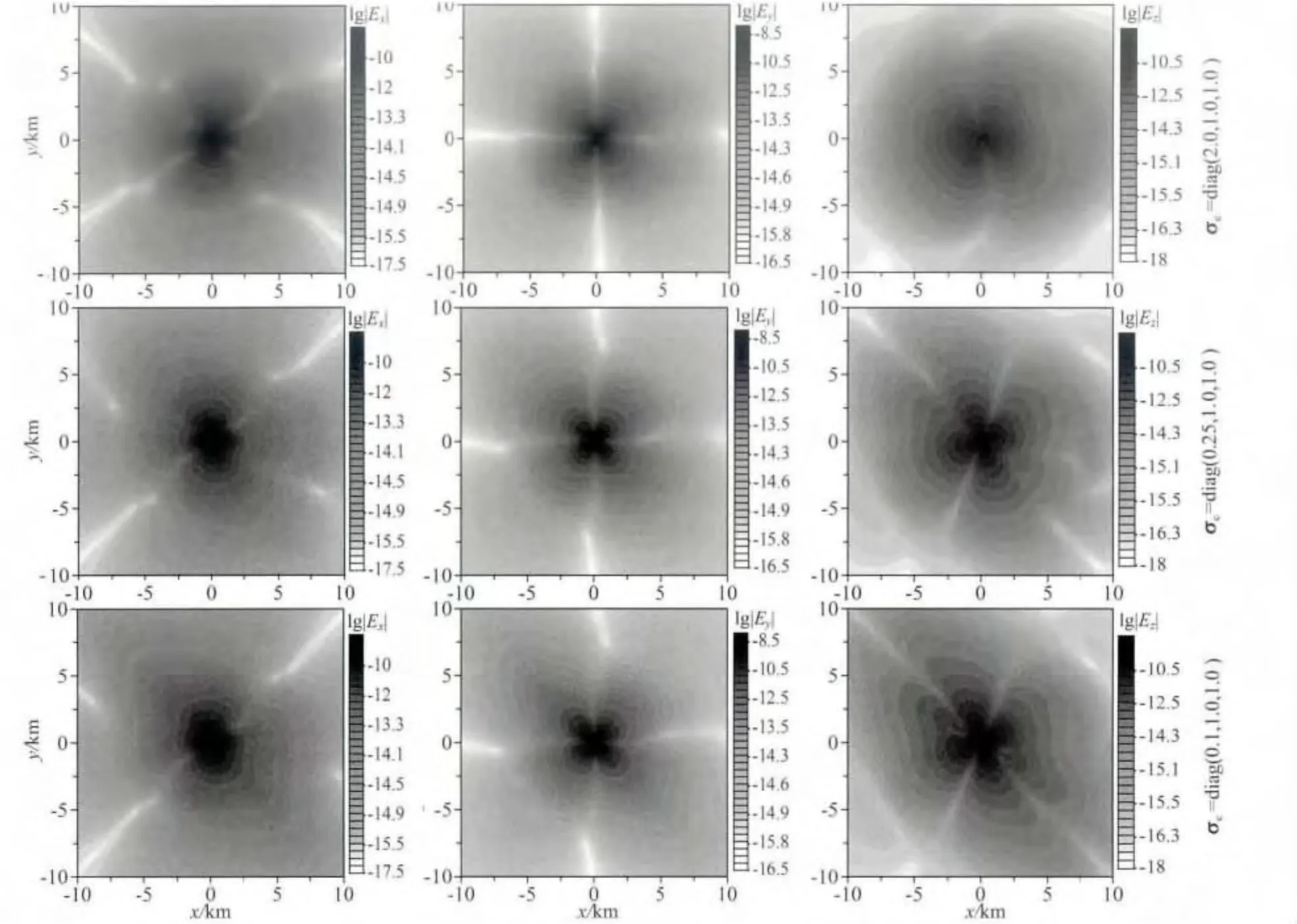
图15 参考电导率张量绕z轴旋转45°时电场分布Fig.15 Plane view of electrical field for reference conductivity tensor rotated around z－axis at 45°

（5）海底电场分布和参考电导率张量的旋转方向存在较强的相关性，为识别海底介质各向异性参数（主轴方向、主轴电导率等）提供依据.本文的计算结果和各向异性影响特征规律对于认识和应用海洋可控源电磁勘查技术具有重要意义，本文的正演算法也为进一步开展海洋可控源电磁法各向异性反演研究奠定了基础.

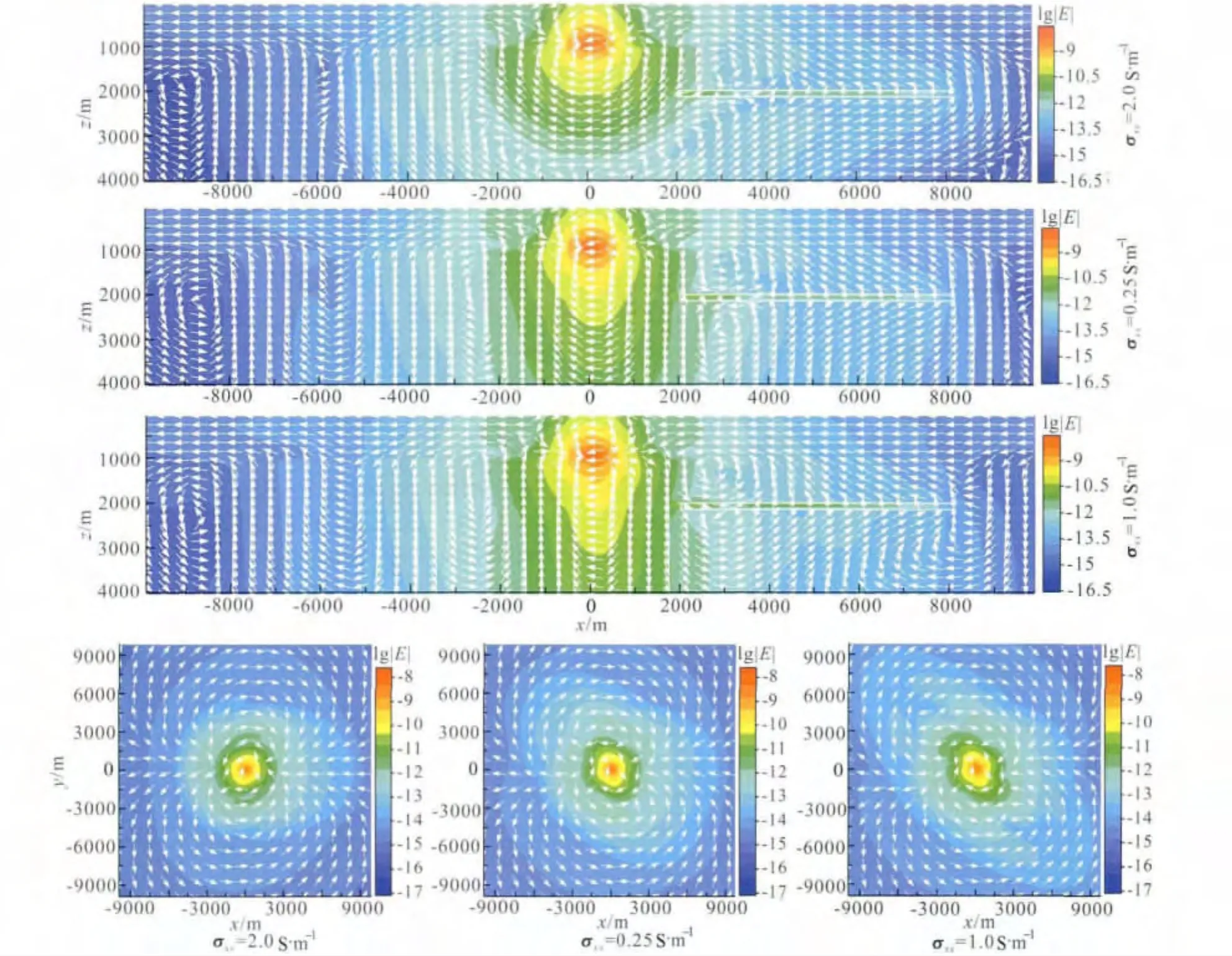
图16 参考电导率张量绕z轴旋转45°时电场和电流分布Fig.16 Distribution of electrical field and current for reference conductivity tensor rotated around z－axis at 45°

致谢 感谢吉林大学电磁“千人计划”研究团队成员的积极支持和帮助，感谢审稿专家和编辑提出的宝贵意见.

Chave A D，Cox C S.1982.Controlled electromagnetic source for measuring electrical conductivity beneath the oceans 1.Forward problem and model study.JournalofGeophysicalReasearch，87（B7）：5372－5338，doi：10.1029／JB087iB07p05327.

Chen G B，Wang H N，Yao J J，et al.2009.Three－dimensional numerical modeling of marine controlled－source electromagnetic responses in a layered anisotropic seabed using integral equation method.ActaPhysicaSinica，58（06）：3848－3857，doi：10.7498／aps.58.3848.

Constable S C，Cox C S.1996.Marine controlled source electromagnetic sounding：2.The PEGASUS experiment.JournalofGeophysicalResearch，101（B3）：5519－5530，doi：10.1029／95JB03738.

Constable S C，Srnka L J.2007.An introduction to marine controlledsource electromagnetic methods for hydrocarbon exploration.Geophysics，72（2）：WA3－WA12，doi：10.1190／1.2432483.

Constable S C.2010.Ten years of marine CSEM for hydrocarbon exploration.Geophysics，75（5）：75A67－75A81，doi：10.1190／1.3483451.

Commer M，Newman G A.2008.New advamces in three－dimensional controlled－source electromagnetic inversion.GeophysicalJournal International，172：513－535，doi：10.1111／j.1365－246X.2007.03660.x.

Cox C S.1980.Electromagnetic induction in the oceans and inferences on the constitution of the earth.GeophysicalSurveys.4（1－2）：137－156，doi：10.1007／BF01452963.

Cox C S.1981.On the electrical conductivity of the oceanic lithosphere.PhysicsoftheEarthandPlanetaryInteriors，25（3）：196－201，doi：10.1016／0031－9201（81）90061－3.

Cox C S，Constable S C，Chave A D，et al.1986.Controlled source electromagnetic sounding of the ocean lithosphere.Nature，320（6）：52－54，doi：10.1038／320052a0.

Crepaldi J L S，Buonora M P P，Figueiredo I.2011.Fast marine CSEM inversion in the CMP domain using analytical derivatives.Geophysics，76（5）：F303－F313，doi：10.1190／geo2010－0237.1

Edwards R N，Chave A D.1986.A transient electric dipole－dipole method for mapping the conductivity of the sea floor.Geophysics，51（4）：984－987，doi：10.1190／1.1442156.

Edwards R N.1997.On theresource evalution of marine gas hydrate deposits using sea－floor transient electric dipole－dipole methods.Geophysics，62（1）：63－74，doi：10.1190／1.1444146.

Eidesmo T，Ellingsurd S，MacGregor L M，et al.2002.Sea bed Logging（SBL），a new method for remote and direct identification of hydrocarbon filled layers in deepwater areas.FirstBreak，20（3）：144－152，doi：10.1046／j.1365－2397.2002.00264.x.

Everett M E，Constable S C.1999.Electric dipole fields over an anisotropic seafloor：theory and application to the structure of 40Ma Pacific Ocean lithosphere.GeophysicalJournalInternational，136：41－56，doi：10.1046／j.1365－246X.1999.00725.x.

Freund R W.1993.A transpose－free quasi－minimal residual algorithm for non－Hermitian linear systems.SIAMJ.Sci.Stat.Comput，14：470－482，doi：10.1137／0914029.

Gellert W，Kuestner H，Hellwich M，et al.1986.Mathematik，VEB BibliographischesInstitut，Leipzig

Gribenko A，Zhdanov M S.2007.Rigorous 3Dinversion of marine CSEM databased on the integral equation method.Geophysics，72（2）：WA73－WA84，doi：10.1190／1.2435712.

Hoversten G M，Morrison H F，Constable S C.1998.Marine magnetotellurics for petroleum exploration，Part II：Numerical analysis of subsalt resolution.Geophysics，63（3）：826－840，doi：10.1190／1.1444394.

HunzikerJ，Slob E，Mulder W.2011.Effects of the airwave in timedomain marine controlled－source electromagnetics.Geophysics，76（4）：F251－F261，doi：10.1190／1.3587222.

Kong F N，Johnstad S E，Røsten T，et al.2008.A 2.5Dfiniteelement－modeling difference method for marine CSEM modeling in stratified anisotropic media.Geophysics，73（1）：F9－F19，doi：10.1190／1.2819691.

Liu C，Zhou F，Lin J.2012.Simulation and analysis on the prospecting capability of marine controlled－source electromagnetic methods to hydrocarbon reservoirs.ChineseJournalofRadio Science，27（4）：747－772.

Liu Y，Yin C，Weng A，et al.2012.Attitude effect for marine CSEM system.ChineseJ.Geophys.，55（8）：2757－2768.doi：10.6038／j.issn.0001－5733.2012.08.027.

Li Y，Dai S.2011.Finite element modelling of marine controlledsource electromagnetic responses in two－dimensional dipping anisotropic conductivity structures.GeophysicalJournal International，185：622－636，doi：10.1111／j.1365－246X.2011.04974.x.

Løseth L O，Ursin B.2007.Electromagnetic fields in planarly layered anisotropic media.GeophysicalJournalInternational，107：44－80，doi：10.1111／j.1365－246X.200703390.x.

Mittet R， Morten J P.2013.The marine controlled－source electromagnetic method in shallow water.Geophysics，78（2）：E67－E77，doi：10.1190geo2012－0112.1.

Newman G A，Alumbaugh D L.1995.Frequency－domain modelling of airbone electromagnetic responses using staggered finite differences.GeophysicalProspecting，43：1021－1042，doi：10.1111／j.1365－2478.1995.tb00294.x.

Newman G A，Commer M，Carazzone J J.2010.Imaging CSEM data in the presence of electrical anisotropy.Geophysics，75（2）：F51－F61，doi：10.1190／1.3295883.

Um E S，Alumbaugh D L.2007.On the physics of the marine controlled－source electromagnetic method.Geophysics，72（2）：WA13－WA26，doi：10.1190／1.2432482.

Weiss C J，Constable S.2006.Mapping thin resistors and hydrocarbons with marine EM methods，PartⅡ—Modeling and analysis in 3D.Geophysics，71（6）：G321－G332，doi：10.1190／1.2356908.

Wiik T，Ursin B，Hokstad K.2013.2.5DEM modelling in TIV conductive media and the effect of anisotropy in normalized amplitude responses.JournalofGeophyscisandEngineering，2013（10）：1－10，doi：10.1088／1742－2132／10／1／015006.

Sasaki Y.2013.3Dinversion of marine CSEM and MT data：An approach to shallow－water problem.Geophysics，78（1）：E59－E65，doi：10.1190／geo2012－0094.1.

Sinba M C，Patel P D，Unsworth M J，et al.1990.An active source electromagnetic sounding system for marine use.MarineGeophysicalResearch，12（1－2）：59－68，doi：10.1007／BF00310563.

Yin C.2006.MMT forward modeling for a layered earth with arbitrary anisotropy.Geophysics，71（3）：G155－G128，doi：10.1190／1.2197492.

Yang B，Xu Y X，He Z X，et al.2012.3Dfrequency－domain modeling of marine controlled source electromagnetic responses with topography using finite volume method.ChineseJ.Geophys.（in China），55（4）：1390－1399.doi：10.6038／j.issn.0001－5733.2012.04.035.

Yin C C，Liu Y H，Weng A H，et al.2012.Research on marine controued－source electromagnetic method airwave.Journalof JilinUniversity（EarthScienceEdition），42（5）：1506－1520，doi：10.6038／j.issn.0001－5733.2012.08.027.

Zhdanov M S.2002.Geophysical inverse theory and regularization problems：Elsevier Science Publ.Co.，Inc.

Zhdanov M S，Lee S K，Yoshioka K.2006.Integral equation method for 3Dmodeling of electromagnetic fields incomplex structures with inhomogeneous background conductivity.Geophysics，71（6）：G333－G345，doi：10.1190／1.2358403.

附中文参考文献

陈桂波，汪宏年，姚敬金等.2009.各向异性海底地层海洋可控源电磁响应三维积分方程法数值模拟.物理学报，58（06）：3848－3857，doi：10.7498／aps.58.3848.

刘长胜，周逢道，林君.2012.海洋可控源电磁法对油气探测能力的仿真分析.电波科学学报，27（4）：747－772.

刘云鹤，殷长春，翁爱华等.2012.海洋可控源电磁法发射源姿态影响研究.地球物理学报，55（8）：2757－2768，doi：10.6038／j.issn.0001－5733.2012.08.027.

杨波，徐义贤，何展翔等.2012.考虑海底地形的三维频率域可控源电磁响应有限体积法模拟.地球物理学报，55（4）：1390－1399，doi：10.6038／j.issn.0001－5733.2012.04.035.

殷长春，刘云鹤，翁爱华等.2012.海洋可控源电磁法空气波研究现状及展望.吉林大学学报（地球科学版），42（5）：1506－1520，doi：10.6038／j.issn.0001－5733.2012.08.027.