基于弹性阻抗的储层物性参数预测方法

印兴耀，崔维，宗兆云，刘晓晶

中国石油大学（华东）地球科学与技术学院，青岛 266580

1 引言

地震数据中蕴含着丰富的储层物性参数信息，而储层物性参数作为衡量储层质量及孔隙承载含流体状况的重要参数，其准确估计能够为储层预测提供有力参考依据，为孔隙流体识别起到一定的指导作用.

针对于储层物性参数反演方法的研究，国内外学者取得一系列研究成果.Doyen（1988）使用协同克里格法用地震数据反演出的声阻抗数据来预测孔隙度参数；McCormack（1991）提出将神经网络技术应用于地球物理领域；国内印兴耀等（1994，1998）将神经网络技术应用到储层预测中；董恩清和高宏亮（1998）提出应用人工神经网络的方法将约束反演得到的波阻抗转换成储层物性参数；由于神经网络有一定的局限性，后来的研究人员对神经网络做了一定程度的改进，田景文综合BP（Back Propagation）的快速收敛和GA（Genetic Algorithm，遗传算法）的全局寻优的特点，将二者有机的结合起来，形成BP－GA混合算法实现薄互储层物性参数预测，该方法能较好地解决预测精度和收敛速度问题（田景文和高美娟，2002）；聂建新等（2004）提出基于同时包含Biot流动和喷射流动这两种力学机制的非饱和多孔隙BISQ模型，利用小生境遗传算法实现储层参数反演，该方法在观测噪声低于5%时，具有很高的精度；Mukerji和Eidsvik提出使用统计岩石物理模型联合地震资料识别储层岩性和流体性质，并做出不确定性分析 （Mukerji et al.，2001a，2001b；Eidsvik et al.，2004）；Spikes等（2007）提出了一种联合地震资料和测井数据的概率地震反演技术实现储层参数预测；Larsen等（2006）将马尔科夫链模型作为流体的先验分布引入到综合的岩性流体预测中；Gallop（2006）应用此方法实现了储层相态的空间预测；Bachrach（2006）将随机岩石物理模型应用于含气砂岩中，联合反演孔隙度及含水饱和度；Buland等（2008）定义一种能够描述弹性参数的空间模型——高斯模型，应用于快速贝叶斯反演方法中实现岩性和流体预测；由于地震资料、测井数据以及岩石物理信息在空间分布，尺度以及与储层的物性关系上的不一致性，Bosch等（2009）提出一种融合地质统计学的方法实现孔隙度以及含水饱和度的预测，在该方法中，用到最小二乘法以及马尔科夫链蒙特卡罗采样技术；Grana和Rossa（2010）提出的反演储层物性参数的方法依然是建立在贝叶斯理论框架之下，建立物性参数的先验分布时假设其服从多分量混合高斯分布，联合统计岩石物理模型，估计物性参数的后验概率分布，完成储层物性参数预测；Ulvmoen和Omre（2010）使用马尔科夫随机场来做流体识别；Rimstand和Omre（2010）在Ulvmoen提出的模型基础上，将其推广到依赖于深度的岩石物理模型并推导出模型参数；Han等（2011）使用一种空间的岩性流体聚类的方法实现了岩性流体预测；Bosch等（2010）提出基于贝叶斯理论框架下的储层物性参数反演方法.

基于贝叶斯理论框架下的储层物性参数反演，大多使用井反演获得的弹性参数进一步来估算物性参数，转换过程中通常需要应用到反演精度相对较差的密度项，从而使间接估算储层参数的精度下降，因此本文在充分利用弹性阻抗反演稳定性的基础上，提出一种基于弹性阻抗的储层物性参数预测方法，这样就避免由于密度反演不准确而使得物性参数反演存在较大的误差.该方法主要应用贝叶斯理论推导出待反演的目标函数，使用蒙特卡罗仿真模拟技术对已建立的储层物性参数的先验分布做随机抽样获取储层物性参数的随机分布样本空间，通过联合多元拟合的方法和Connolly弹性阻抗方程建立可以表征弹性阻抗参数和储层物性参数之间关系的统计性岩石物理模型.该方法增加了反演的稳定性以及横向连续性等优势，达到稳定反演储层物性参数的目的.

2 贝叶斯理论框架下目标函数的建立

贝叶斯理论包括三个基本概念：先验分布，后验分布以及联系二者的似然函数.贝叶斯分类器的基本分类原理是通过某对象的先验概率，利用贝叶斯公式计算出其后验概率，即该对象属于某一类的概率，选择具有最大后验概率的类作为该对象所属的类.也就是说，贝叶斯分类器是最小错误率意义上的优化.

在储层物性参数反演过程中，将待反演的目标函数（储层物性参数：孔隙度，泥质含量，含水饱和度）与已知的观测数据（弹性阻抗参数）通过贝叶斯公式联系起来，如下所示：

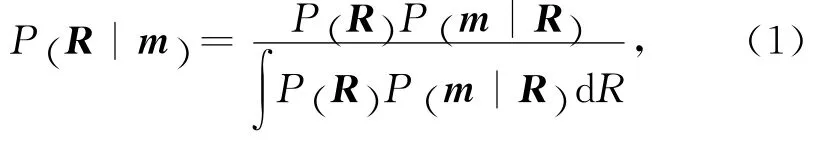
其中：R代表物性参数，即Sw分别表示孔隙度，泥质含量，含水饱和度；m代表弹性阻抗参数，即分别表示三个角度的弹性阻抗；P（·）代表概率密度函数.

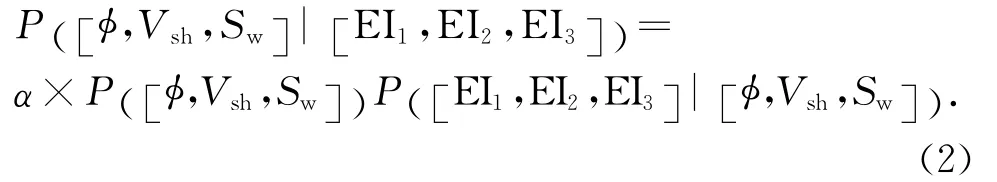
由于三个角度的弹性阻抗之间具有相关性，且角度差异越小，相关性越高，反演的稳定性越差，因此，在合理范围内，尽量选取三个角度差异相对较大的弹性阻抗参数，并做去相关处理，使三个角度的弹性阻抗参数之间彼此相互独立，即

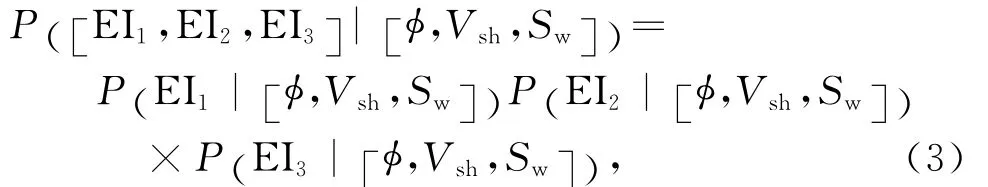
式中，EI1，EI2与EI3均代表去相关处理之后的弹性阻抗数据.

取最大后验概率位置处所对应的目标参数作为储层物性参数的最终反演结果

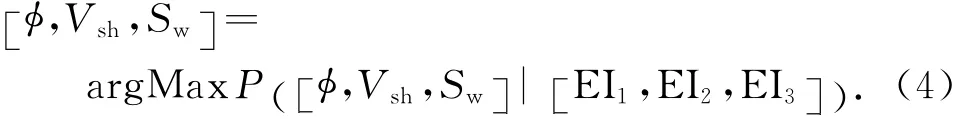
将（2）式，（3）式代入（4）式中，由于常数项对于最终反演结果没有作用，因此可以舍弃常数项，即可获得最终反演的目标函数：

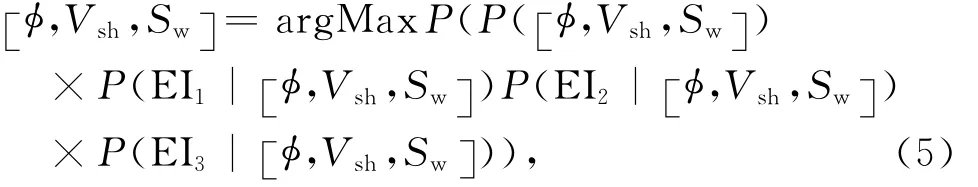
P）为在储层物性参数反演过程中，联系先验分布和后验概率分布的似然函数，可以通过建立的统计岩石物理模型和蒙特卡罗仿真模拟技术来完成.

3 基于弹性阻抗的储层物性参数反演

常规的基于贝叶斯分类的储层物性参数反演方法（Grana and Rossa，2010），利用反演得到的弹性参数进一步估算物性参数，实现了多种储层物性参数的联合反演，但弹性参数中的密度信息很难准确获取.为了解决密度获取不准确这一问题，本文提出使用弹性阻抗反演储层物性参数，避免反演过程中密度项的使用.

基于弹性阻抗的储层物性参数反演是在贝叶斯理论框架下，应用统计岩石物理模型，蒙特卡罗随机抽样方法以及期望最大化算法相结合共同完成储层物性参数反演.

通过对测井数据做统计分析，建立近似符合实际测井资料的储层物性参数的先验分布（如多分量高斯分布，均匀分布等），在本文中，选择多分量混合高斯分布；并通过蒙特卡罗仿真模拟技术对已建立的先验概率分布进行离散的随机抽样，可获得储层物性参数的随机样本空间分布；同时根据实际测井资料信息以及已有的岩石物理理论作为指导，建立能够表征弹性阻抗参数和储层物性参数之间的关系式，即确定性岩石物理关系.

通常确定性岩石物理关系的构建有以下三种方法：通过岩石物理学的基本理论，经典岩石物理模型以及实际测井资料拟合的关系式.由于经典岩石物理模型并不具备普遍的适用性，因此，在实际资料的应用中，通常对测井资料进行统计分析，构建一种岩石物理关系，使其与实际测井资料匹配程度达到最佳状态.

在实际资料处理中，弹性参数（纵波速度，横波速度，密度等）与物性参数（孔隙度，泥质含量，含水饱和度等）二者之间的关系多数为非线性的，可以通过曲线拟合的方式得到，如高斯拟合，多项式拟合等.在误差允许条件下可以将其视为线性关系，如（6）式所示.

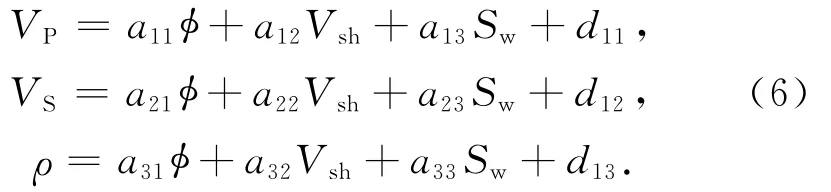
可写成矩阵的形式：

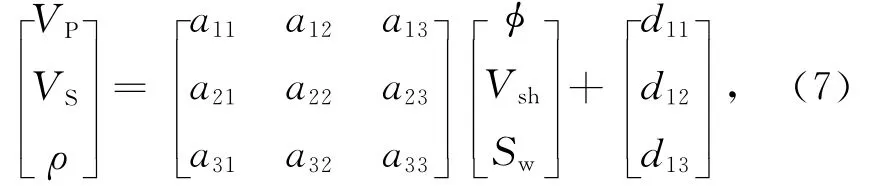
式中的矩阵系数aij（i＝1，2，3；j＝1，2，3）以及常数项d1j（j＝1，2，3）可以利用测井资料通过多元回归的方法拟合得到.

当弹性参数与物性参数二者之间的关系无法近似为线性时，采用多项式拟合，则方程（6）变为多元高次方程组：

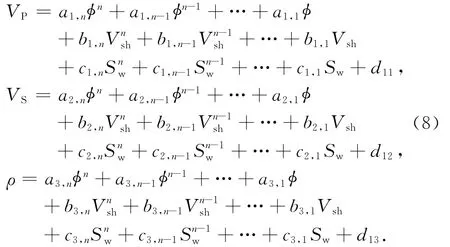
同理，利用已知的测井资料通过最小二乘拟合可以得出（8）式中的ai，j、bi，j、ci，j与d1，i，其中i＝1，2，3；j＝1，2，…，n.

在得到弹性参数与物性参数之间确定性关系的基础上，结合弹性阻抗方程构建弹性阻抗与物性参数之间的关系.Connolly（1999）推导的弹性阻抗方程如下：

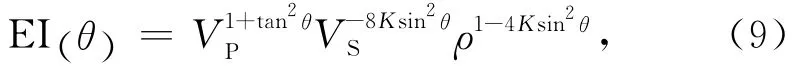
Whitcombe（2002）对（9）式的弹性阻抗方程进行归一化处理：

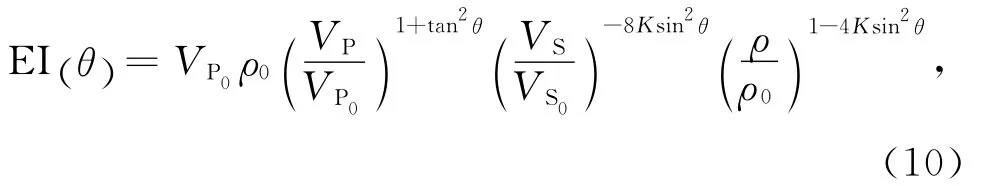
其中，K是一个常数，K＝ （VS／VP）2，通常取0.25.本文进一步对（10）式两边取对数：

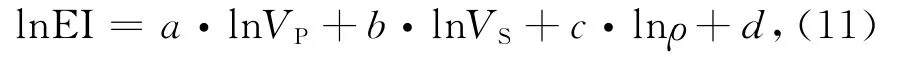
其中，a＝1＋tan2θ；b＝－8Ksin2θ；c＝1－4Ksin2θ；常数项d＝－tan2θ·lnVP0＋8Ksin2θ·lnVS0＋4Ksin2θ·lnρ0，VP0，VS0，ρ0分别为纵波速度，横波速度，密度测井曲线的均值.

假定三个不同角度θ1，θ2，θ3的弹性阻抗分别记为EI1，EI2，EI3，则

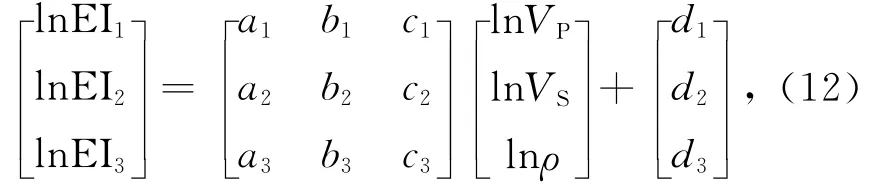
式中，ai，bi，ci，di（i＝1，2，3）分别为三个角度弹性阻抗中lnVP，lnVS，lnρ对应的系数及相应的常数项.

综合式（7）和式（12）（弹性参数与物性参数可近似为线性关系）或式（8）和式（12）（弹性参数与物性参数不可近似为线性关系），即可求出弹性阻抗与物性参数之间的直接关系，进而可以获取确定性岩石物理关系式.

在实际的地震勘探中，地下储层条件是复杂多变的，考虑到不同的孔隙结构、矿物颗粒磨圆度、地层温度、压力条件的微弱变化以及泥质含量等诸多因素（胡华锋等，2012）都有可能对弹性阻抗与储层物性参数之间的岩石物理关系造成一定程度的偏差，因此，为了降低这些因素的影响，引入随机误差.确定性岩石物理关系和随机误差就构成了统计岩石物理模型，其数学表达式为：

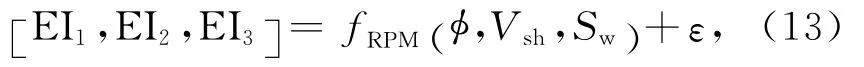
其中，fRPM表述弹性阻抗参数和储层物性参数之间的确定性岩石物理关系，ε代表为确定性岩石物理关系添加的误差项，可以通过实际测井资料与确定性岩石物理关系之间的相对差异来估算，常选取均值为零的高斯截断误差，以此来削弱地下复杂结构对二者关系的影响，继而完成建立统计岩石物性模型的工作.

综上两步，利用储层物性参数的随机样本分布空间和统计岩石物理模型，即可获得弹性阻抗参数的随机分布样本空间分布，并做横向外推.至此，由二者的随机样本分布空间就共同构成了储层物性参数与弹性阻抗参数的联合分布的空间样本.通过期望最大化算法估算联合分布中的各项参数，结合从叠前地震数据反演得到的弹性阻抗数据体，可估算储层物性参数的后验条件概率，寻找最大后验概率位置处所对应的储层物性参数值，该值即为最终的储层物性参数反演结果.图1是利用弹性阻抗实现储层物性参数反演的流程图.

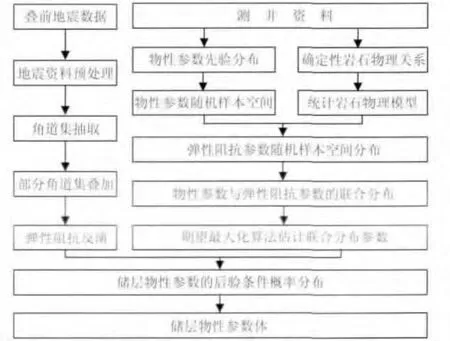
图1 弹性阻抗反演储层物性参数流程图Fig.1 Flowchat of petrophysical－property inversion based on elastic impedance

4 模型测试

为了验证基于弹性阻抗反演储层物性参数这一反演方法的可行性，做如下模型测试.

选取某井上深度范围为2460～2513m的一段地层作为研究目标层.图2A是该井上的物性参数测井曲线，图2B是该井上的弹性参数测井曲线.

根据公式（7）和公式（11）建立一种确定性岩石物理关系式表征弹性阻抗参数与物性参数之间的关系.为验证确定性岩石物理关系建立的准确性，将其应用到前面已选择的地层模型中.如图3所示，实线代表利用测井曲线中的弹性参数曲线计算的三个角度的弹性阻抗值，即弹性阻抗的计算值；虚线代表利用确定性岩石物理关系和测井曲线中的物性参数曲线拟合的三个角度的弹性阻抗值，即拟合值.从图中可以观察到，利用所建立的确定性岩石物理关系拟合的弹性阻抗参数与储层物性参数之间的关系的准确度较高，相关度达到90.14%，这也说明了确定性岩石物理关系建立的准确性与合理性.

由于在确定性岩石物理关系式建立过程中，近似运算的使用以及其他条件的影响，都将导致确定性岩石物理关系式拟合的弹性阻抗曲线与实际根据测井数据计算出来的值存在一定程度上的偏差，为了削弱这种偏差的存在对反演过程造成的影响，为此为建立的岩石物理关系式添加随机误差项，本文取均值为零的高斯截断误差.

根据实际的测井数据做统计分析，建立储层物性参数的先验分布，可假设储层物性参数（孔隙度，泥质含量，含水饱和度）服从三项高斯分量的混合高斯分布，并用期望最大化算法计算出先验分布的各项参数（均值，标准差以及各项所占的权值），然后应用蒙特卡罗仿真模拟技术对其进行随机抽样，获得储层物性参数的随机样本分布图.

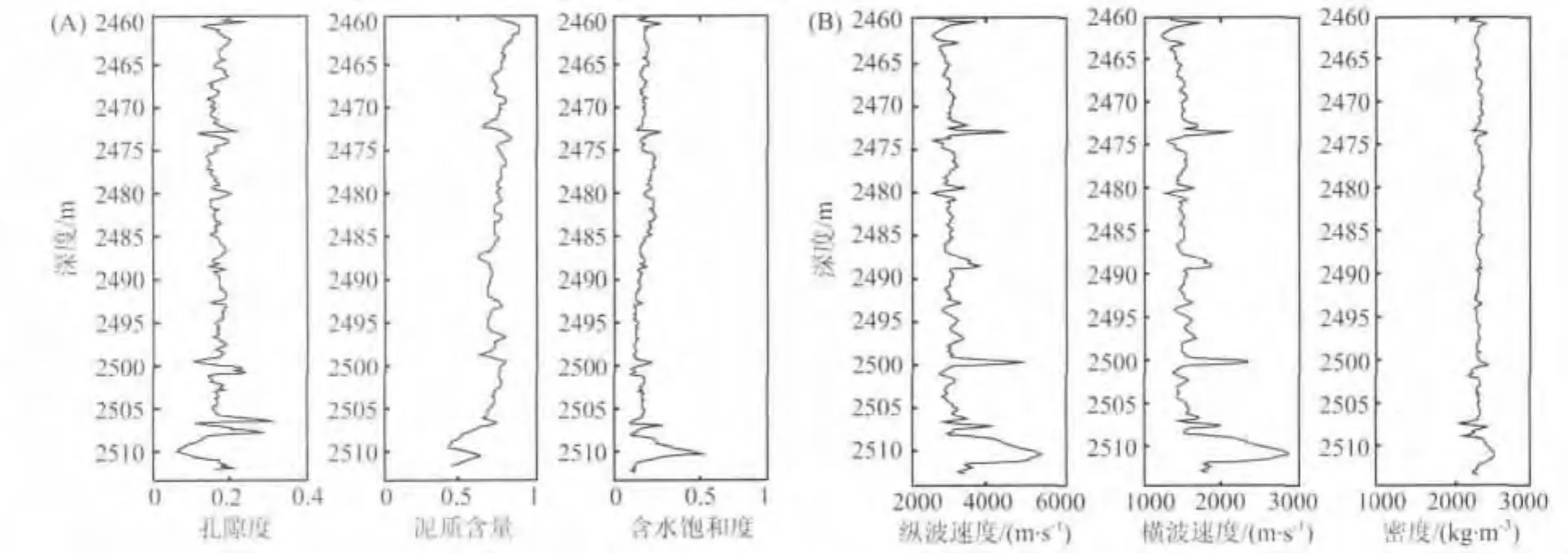
图2 模型储层物性参数测井曲线（A）和弹性参数测井曲线（B）Fig.2 Petrophysical parameter curves（A）and elastic parameter curves（B）of the model

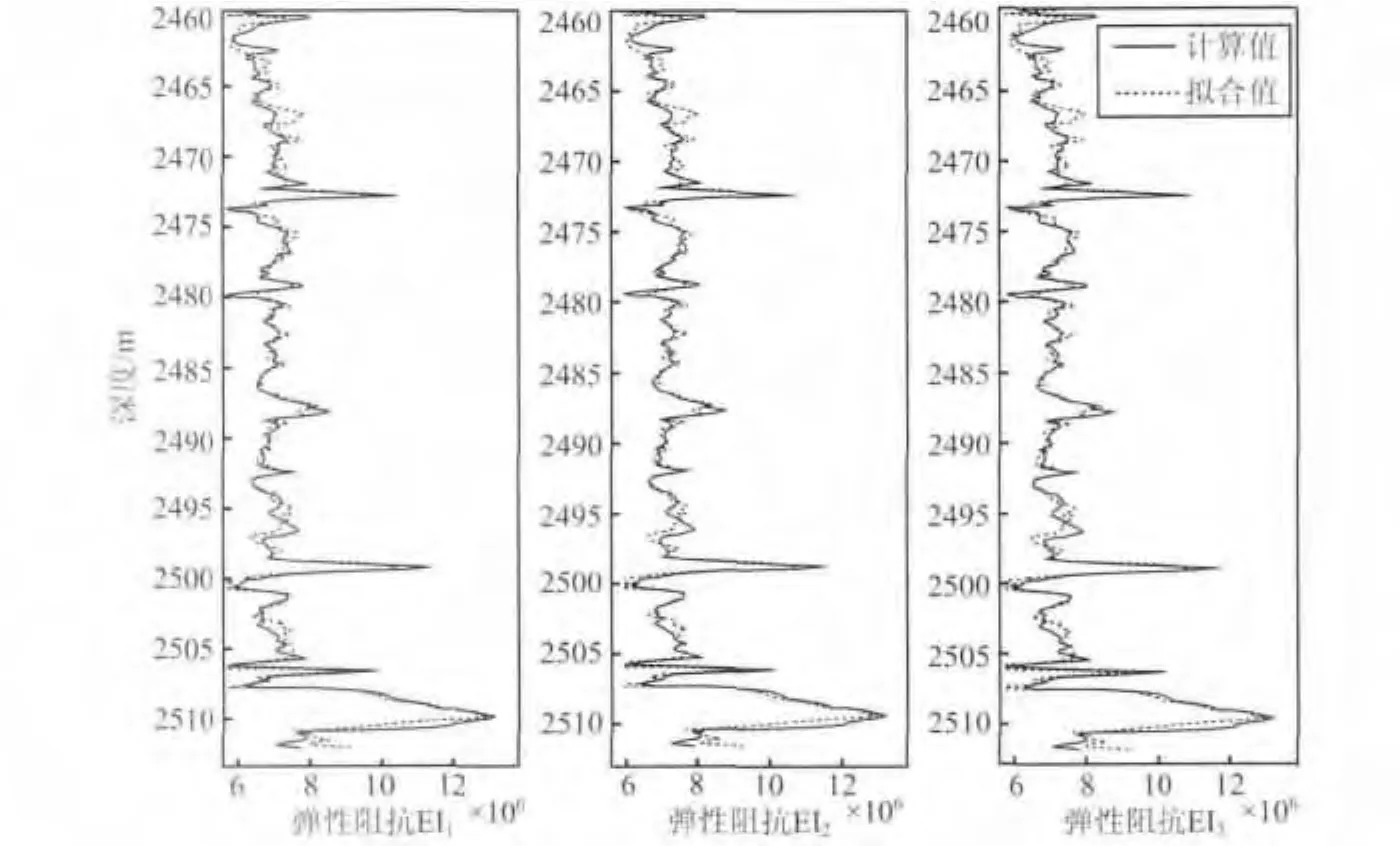
图3 确定性岩石物理关系验证Fig.3 Verification of physical relationship of rock

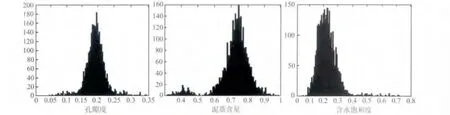
图4 物性参数的先验分布Fig.4 Prior distribution of petrophysical parameters

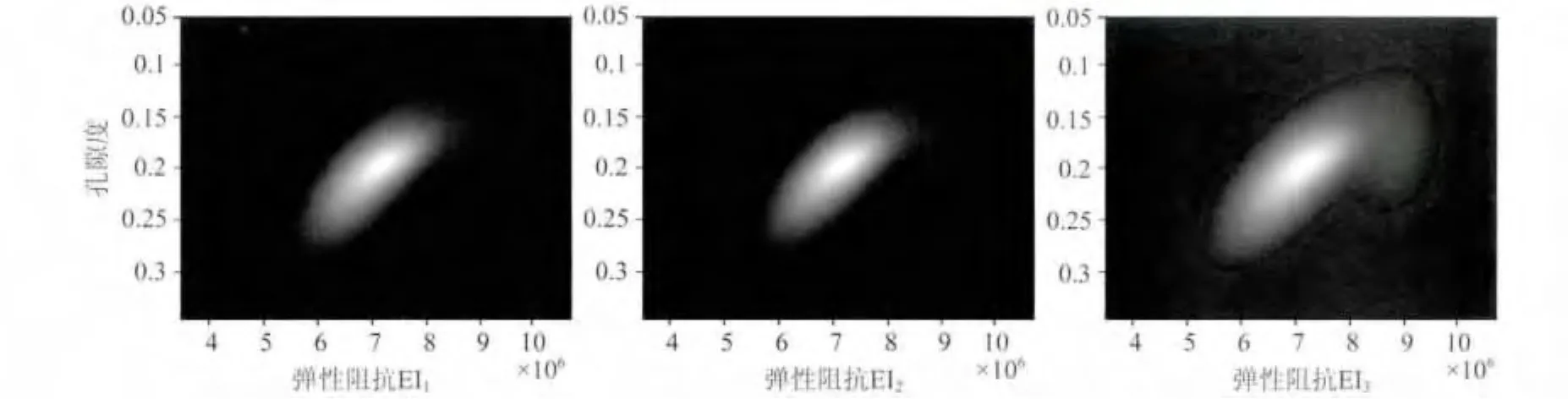
图5 孔隙度与三个角度弹性阻抗的联合分布Fig.5 Joint distribution of porosity and elastic impendance with three angles

已知储层物性参数先验分布随机样本中的每一个样点，根据所建立的统计岩石物理模型，求取出每一个样点所对应的弹性阻抗参数的值，就可获得弹性阻抗参数的随机分布样本空间.将物性参数随机样本空间与弹性阻抗参数随机样本空间相结合，即可获得储层物性参数和弹性阻抗参数的联合分布.图5为三个角度的弹性阻抗参数与孔隙度的联合分布情况，从黑色调到白色调渐变的过程表征孔隙度后验条件概率由小变大的过程.

应用期望最大化算法计算出孔隙度与三个角度的弹性阻抗参数的联合分布中三个高斯分量的各项参数（均值，标准差，权值），并分别求取在已知三个角度弹性阻抗参数的前提下，孔隙度的后验条件概率，即对三个角度的弹性阻抗参数做去相关处理，使彼此之间相互独立，然后应用式（13）计算出在弹性阻抗参数已知的条件下孔隙度的后验概率，即

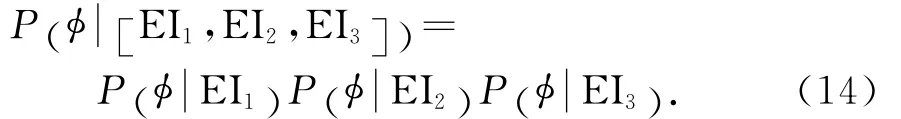
根据应用贝叶斯公式推导出来的待反演目标函数，估计孔隙度后验条件概率的最大值，并且寻找最大值位置处所对应孔隙度的值，该值即为孔隙度的最终反演结果.泥质含量和含水饱和度的反演方法与孔隙度的反演方法相同.

图6为孔隙度后验概率分布图；图7为孔隙度的最终反演结果.在图7中，实线表示实际测井资料中提供的孔隙度测井曲线，虚线则代表应用本文介绍的方法反演出的孔隙度曲线.从图中可以看出，反演出的孔隙度曲线与实际测井资料中提供的孔隙度曲线吻合程度较好，经计算，相关度达到90.56%，这说明了该反演方法的可行性.

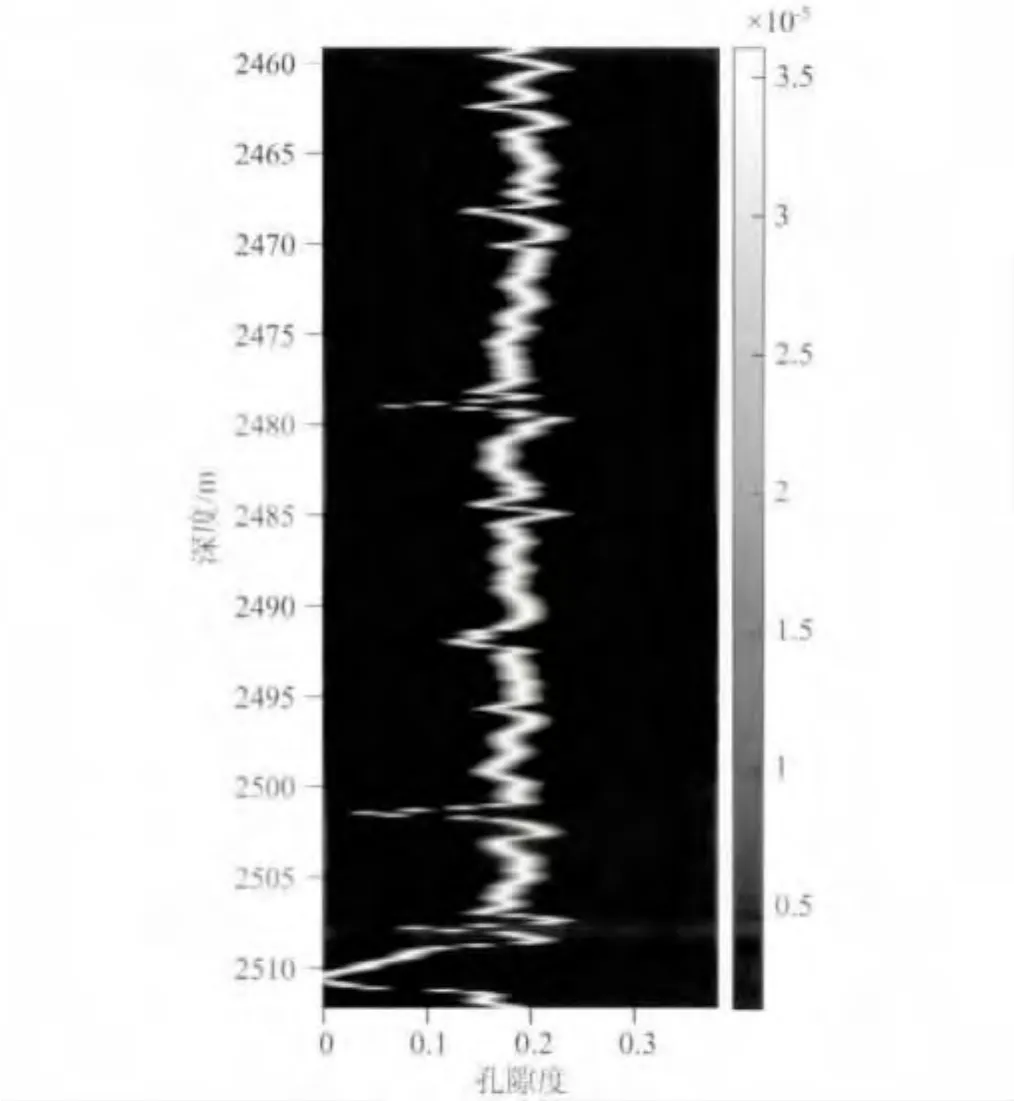
图6 孔隙度后验概率分布图Fig.6 Posterior probability distributions of porosity

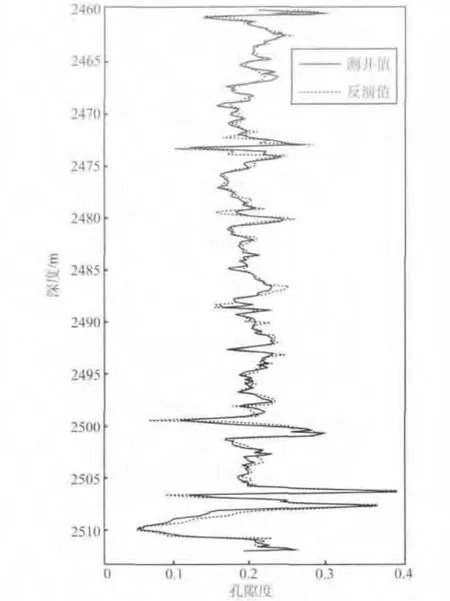
图7 孔隙度反演结果Fig.7 Result of porosity inversion

5 实际数据应用

选取某一工区作为目标区，将上面的方法应用于实际工区中.图8为对确定性岩石物理关系式的验证.实线表示利用测井数据中弹性参数曲线计算的弹性阻抗曲线，虚线表示通过已建立的确定性岩石物理关系式和实际测井数据中物性参数测井曲线拟合的弹性阻抗曲线.从图中可以很明显地看出，拟合值与实际计算值吻合度较高，相关度为92.12%，这就验证了所建立的确定性岩石物理关系式的正确性.

图9为反演出的孔隙度曲线，其中实线代表实际测井值，虚线代表反演值，从图中可以看出，反演的孔隙度曲线与实际测井曲线较为吻合，经计算，二者的相关度为92.34%.

图10为某实际工区中A井与B井的连井地震剖面.在A井，B井中，灰色代表砂岩，白色代表泥岩.其中，A井包含全套测井曲线（储层物性参数及岩石弹性参数测井曲线），B井测井曲线不全，但存在岩性解释结果及油气解释结果.因此，A井为反演参与井，B井不参与反演，作为检验储层物性参数反演的验证井.图11为使用本文介绍的基于弹性阻抗参数反演储层物性参数的方法反演出的孔隙度剖面.从图11中可以看出，孔隙度的高值处正对应于井中砂岩较为发育区段，而孔隙度的低值处对应井中泥岩区段，因此，孔隙度剖面的反演结果与测井解释结果吻合得较好.通过图10和图11对比发现，在地震数据剖面箭头所指位置连续性稍差，而反演得到的孔隙度剖面在同一位置处的横向连续性稍有改善，因此，该方法也能够在一定程度上改善物性反演结果的连续性.

6 结论

本文提出的基于弹性阻抗预测储层物性参数的反演方法，以贝叶斯理论作为指导，建立能够表征弹性阻抗与储层物性参数之间关系的统计岩石物理模型，联合蒙特卡罗仿真模拟技术以及期望最大化算法，完成储层物性参数反演.模型测试与实际资料应用表明该方法不仅保留了常规基于贝叶斯的储层物性参数预测方法的优点，而且还具有精确度高，稳定性强以及横向连续性较好等优势，改善了常规获取弹性参数的不确定性，达到稳定反演储层物性参数反演的目的.

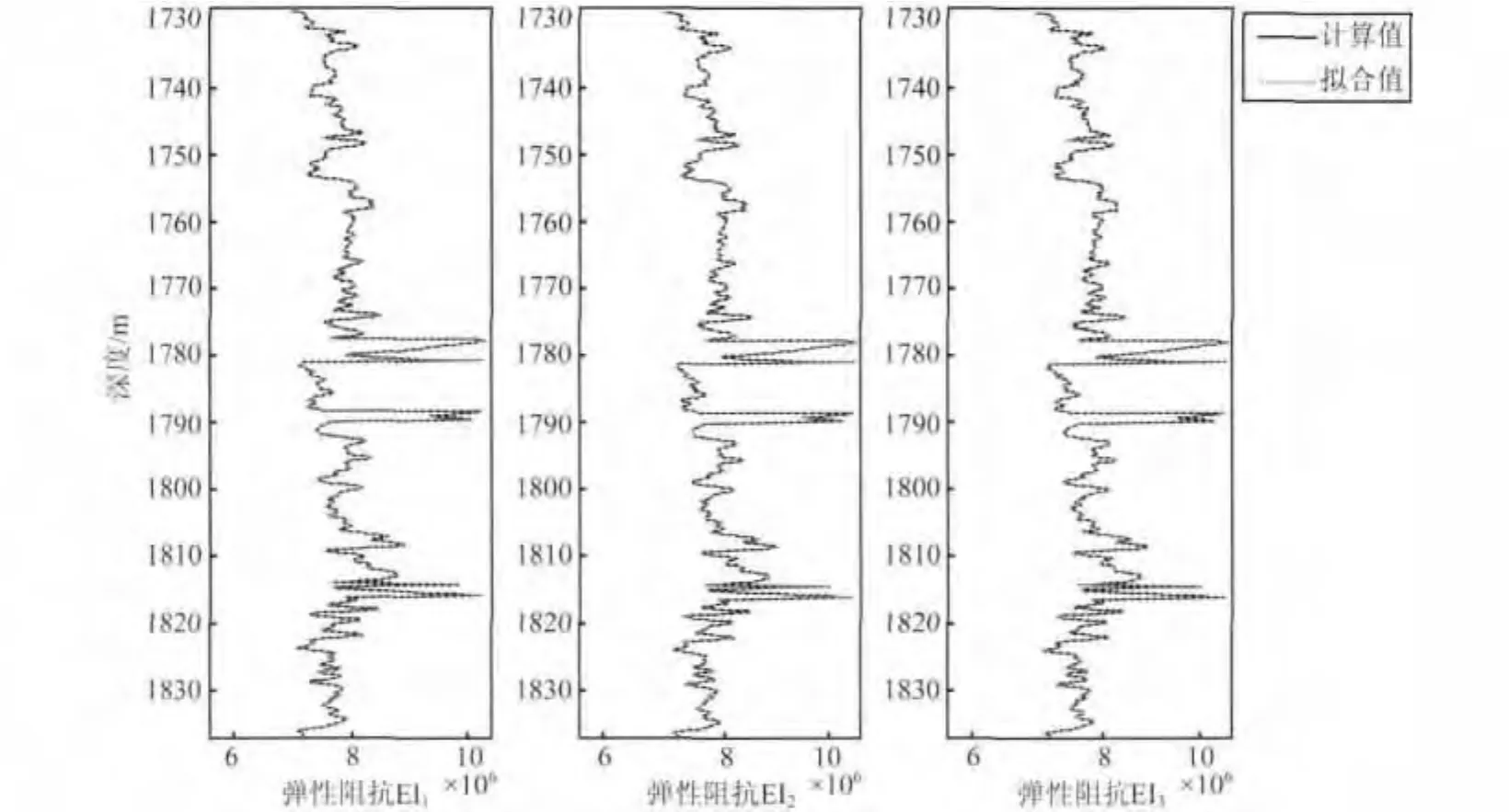
图8 确定性岩石物理关系验证Fig.8 Verification of deterministic physical relationship of rock

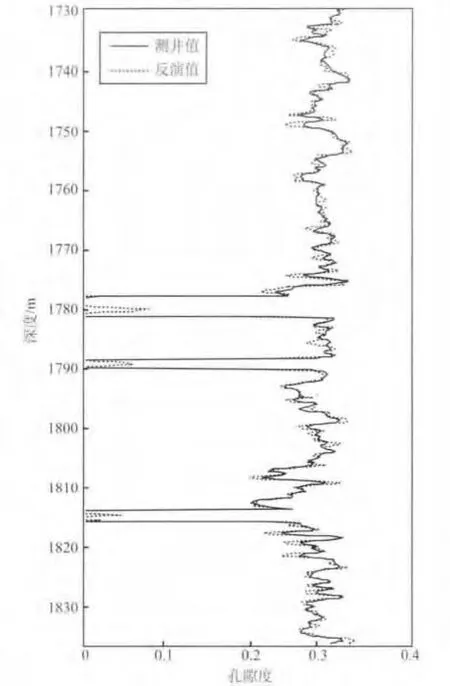
图9 孔隙度反演曲线Fig.9 Curves of porosity inversion

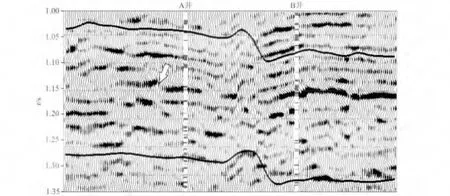
图10 地震剖面Fig.10 Seismic profile

图11 基于弹性阻抗参数反演储层物性参数Fig.11 Estimated petrophysical parameters of reservoirs based on elastic impendance

Bachrach R.2006.Joint estimation of porosity and saturation using stochastic rock－physics modeling.Geophysics，71（5）：O53－O63.

Bosch M，Carvajal C，Rodrigues J，et al.2009.Petrophysical seismic inversion conditioned to well－log data： Methods and application to a gas reservoir.Geophysics，74（2）：O1－O15.

Bosch M，Mukerji T，Gonzalez E F.2010.Seismic inversion for reservoir properties combining statistical rock physics and geostatistics：A review.Geophysics，75（5）：75A165－75A166.

Buland A，Kolbjørnsen O，Hauge R，et al.2008.Bayesian lithology and fluid prediction from seismic prestack data.Geophysics，73（3）：C13－C21.

Connolly P.1999.Elastic impedance.TheLeadingEdge，18（4）：438－452.

Dong E Q，Gao H L.1998.Wave impedance constrain inversion and calculation method of reservoir petrophysical parameters.Well LoggingTechnology（in Chinese），22（5）：337－340.

Doyen P M.1988.Porosity from seismic data：A geostatistical approach.Geophysics，53（10）：1263－1275.

Eidsvik J，Avseth P，Omre H，et al.2004.Stochastic reservoir characterization using prestack seismic data.Geophysics，69（4）：978－993.

Gallop J.2006.Facies probability from mixture distributions with non－stationary impedance errors.2006SEG Annual Meeting.

Grana D，Rossa E D.2010.Probabilistic petrophysical－properties estimation integrating statistical rock physics with seismic inversion.Geophysics，75（3）：O21－O37.

Han M，Zhao Y，Li G M，et al.2011.Application of EM algorithms for seismic facices classification.Computational Geosciences，15（3）：421－429.

Hu H F，Yin X Y，Wu G C.2012.Joint inversion of petrophysical parameters based on Bayesian classification.Geophysical ProspectingforPetroleum（in Chinese），51（3）：225－232.

Larsen A L，Ulvmoen M，Omre H，et al.2006.Bayesian lithology／fluid prediction and simulation on the basis of a Markov－chain prior model.Geophysics，71（5）：R69－R78.

McCormack M D.1991.Neural computing in geophysics.The LeadingEdge，10（1）：11－15.

Mukerji T，Avseth P，Mavko G，et al.2001a.Statistical rock physics：Combining rock physics，information theory，and geostatistics to reduce uncertainty in seismic reservoir characterization.TheLeadingEdge，20（3）：313－319.

Mukerji T，Jørstad A，Avseth P，et al.2001b.Mapping lithofacies and pore－fluid probabilities in a North Sea reservoir：Seismic inversions and statistical rock physics.Geophysics，66（4）：988－1001.

Nie J X，Yang D H，Yang H Z.2004.Inversion of reservoir parameters based on the BISQ model in partially saturated porous media.ChineseJournalofGeophysics（in Chinese），47（6）：1101－1105.

Rimstad K，Omre H.2010.Impact of rock－physics depth trends and Markov random fields on hierarchical Bayesian lithology／fluid prediction.Geophysics，75（4）：R93－R108.

Spikes K，Mukerji T，Dvorkin J，et al.2007.Probabilistic seismic inversion based on rock－physics models.Geophysics，72（5）：R87－R97.

Tian J W，Gao M J.2002.Thin interbedded reservoir parameters predicting based on high speed and precise genetic algorithm neural network.ControlandDecision（in Chinese），17（5）：599－603.

Ulvmoen M，Omre H.2010.Improved resolution in Bayesian lithology／fluid inversion from prestack seismic data and well observations：Part 1—Methodology.Geophysics，75（2）：R21－R35.

Whitcombe D N.2002.Elastic impedance normalization.Geophysics，67（1）：60－62.

Yin X Y，Wu G C，Zhang H Z.1994.The application of neural networks in the reservior prediction.JournaloftheUniversity ofPetroleum（in Chinese），18（5）：20－26.

Yin X Y，Yang F L，Wu G C.1998.Application of neural network to predicting reservoir and calculating thickness in CB oilfield.JournaloftheUniversityofPetroleum（in Chinese），22（2）：17－20.

附中文参考文献

董恩清，高宏亮.1998.波阻抗约束反演及储层物性参数计算方法.测井技术，22（5）：337－340.

胡华锋，印兴耀，吴国忱.2012.基于贝叶斯分类的储层物性参数联合反演方法.石油物探，51（3）：225－232.

聂建新，杨顶辉，杨慧珠.2004.基于非饱和多孔隙介质BISQ模型的储层参数反演.地球物理学报，47（6）：1101－1105.

田景文，高美娟.2002.基于快速、高精度遗传算法神经网络的薄互储层参数预测.控制与决策，17（5）：599－603.

印兴耀，吴国忱，张洪宙.1994.神经网络在储层横向预测中的应用.石油大学学报：自然科学版，18（5）：20－26.

印兴耀，杨风丽，吴国忱.1998.神经网络在CB油田储层预测和储层厚度计算中的应用.石油大学学报：自然科学版，22（2）：17－20.