A noninteracting control strategy for the robust output synchronization of linear heterogeneous networks

Saman KHODAVERDIAN,Jürgen ADAMY

Institute of Automatic Control and Mechatronics,Control Methods and Robotics Lab,Technische Universität Darmstadt,Landgraf-Georg-Str.4,64283 Darmstadt,Germany

A noninteracting control strategy for the robust output synchronization of linear heterogeneous networks

Saman KHODAVERDIAN†,Jürgen ADAMY

Institute of Automatic Control and Mechatronics,Control Methods and Robotics Lab,Technische Universität Darmstadt,Landgraf-Georg-Str.4,64283 Darmstadt,Germany

This paper deals with the problem of robust output synchronization for heterogeneous multi-agent systems.First,a new synchronization approach is presented to synchronize the outputs of heterogeneous agents.Based on noninteracting control techniques,a method is derived for homogenizing the input-output behavior of every agent.Hence,applying the same reference input signal to every agent leads to synchronization.Furthermore,a strategy for increasing the robustness of the synchronization process against exogenous disturbances is presented,which leads to a structurally constrained optimization problem.However,by a convenient reformulation of the problem,well established tools from robust control theory can be used.Moreover,it is shown that this procedure allows to separate the robustness issue from the synchronization task.The effectiveness of the approach is illustrated by a robust output synchronization example for a heterogeneous aircraft fleet.

Heterogeneous networks;Multi-agent systems;Decentralized control;Robust synchronization;Disturbance rejection;Controller constraints and structure

1 Introduction

This paper deals with the robust output synchronization problem for linear heterogeneous multi-agent systems.Here,a multi-agent systems is considered as a cluster of dynamic systems that can exchange information with each other through a communication network.Recently,the problem of cooperative control of such multi-agent systems has received great attention.Topics like cooperative exploration and surveillance,hazardous material handling,distributed sensor networks,vehicle formation control and many more have beeninvestigated.The articles[1]and[2]provide a detailed overview of the applicability of such networked systems.A main problem for these tasks relies on the synchronization of the systems or agents,i.e.,finding a state agreement.Moreover,in general we are interested in decentralized solutions,meaning that there is no central entity that controls every single agent in the network.In centralized solutions,the break down of the central entity will destroy the whole control task,while in decentralized solutions,the control task can still be satisfied despite of malfunctions of single agents.

In the last decade,there have been achieved many results for the synchronization of linear agents.Most of the literature focuses on identical or homogeneous agents[3–6].However,from a practical point of view the consideration of non-identical or heterogeneous agents is more interesting.This is due to the fact that in real world applications no two systems are exactly identical and the consideration of agents with individual dynamics provides a broader range of possible applications.While in homogeneous networks the task is to achieve state synchronization,meaning that all internal states of the agents are synchronized,in a heterogeneous network the agents’internal states may not be physically comparable.Thus,in general the aim is to synchronize a common subset of the agents’states,which is known as partial-state or output synchronization.First examinations of this problem are given in[7]and[8],where the output synchronization problem is ascribed as an output tracking problem and solved by the well-known output regulation theory[9].

Besides the basic problem of achieving state or output agreement among all agents,the problem of robust(output)synchronization is an important property that needs to be investigated.Taking exogenous disturbances into account,the robustness of the synchronization process can be increased.A convenient method for considering robustness issues is provided by the H∞theory.In[10],the H∞control method has been used to synchronize agents with simple integrator dynamics that are subject to exogenous disturbances.Recently,in[11]this problem has been solved by a dynamic optimization approach.The more sophisticated problem of achieving robust synchronization for agents with general linear dynamics and exogenous disturbances has been investigated in[12,13].However,only homogeneous agents have been considered.The problem of robust output synchronization for heterogeneous agents has been considered in[14],where the solution relies on the output regulation theory.

In this work,we propose a new two-step design scheme for solving the robust output synchronization problem of heterogeneous agents subject to exogenous disturbances.This article extends the results presented in[15]and provides some new insights into the topic.In contrast to current methods,where usually the output regulation theory is used,our approach is based on a noninteracting control strategy.With the help of the noninteracting control technique,we first homogenize the input-output behavior of everyagent.Then,applying the same reference input signal leads to output synchronization.This reference input is generated by synchronizing identical exosystems that produce the desired synchronization trajectory.In a second step,we will show that this approach allows to separate the robust output synchronization problem into a simple synchronization task for homogeneous systems and a robust input-output homogenization issue,which will be reformulated as a standard control problem.This strategy results in a structurally constrained optimization problem and,hence,might be non-convex.Albeit,solvers such as HIFOO[16,17],which use non-smooth optimization techniques,are well applicable to solve the problem.

The rest of the paper is structured as follows:in the next section,some preliminaries are introduced and a formal problem description is provided.In Section 3,the basic idea of synchronizing heterogeneous agents by the noninteracting control method is presented.In Section 4,we point out that there exist some degrees of freedom that can be optimized in a way such that the robustness of the synchronization process with respect to exogenous disturbances is increased.For this purpose,the optimization problem has to be reformulated as a standard control problem.To illustrate the applicability of the proposed approach,an example demonstrating the robust output synchronization for a fleet of heterogeneous aircraft is presented in Section 5,followed by a conclusion in Section 6.

2 Preliminaries and problem setup

2.1 Notation and matrix theory

The following notations will be used throughout this paper:scalar values are represented by italic letters and vectors and matrices by boldface letters.The identity matrix of order p is written as Ip,a zero matrix of appropriate dimension as 0 and a vector of ones as 1.

Furthermore,we define the set of natural numbers by N={1,2,...}.A diagonal matrix H,with diagonal entries h1,...,hN,is written as H=diag{h1,...,hN}.The transpose of a matrix M reads MT,and if it is square and regular,M−1denotes its inverse.The jth eigenvalue of M is written as λj(M).Furthermore,M is called Hurwitz if all of its eigenvalues have strictly negative real part and it is called anti-stable if all of its eigenvalues have non-negative real part.

The space of square integrable vector functions over[0,∞)is denoted by L2[0,∞).For a stable linear system with state space model˙x=Ax+Bu,y=Cx+Du and transfer matrix,the H∞norm from the input vector u to the output vector y is defined as

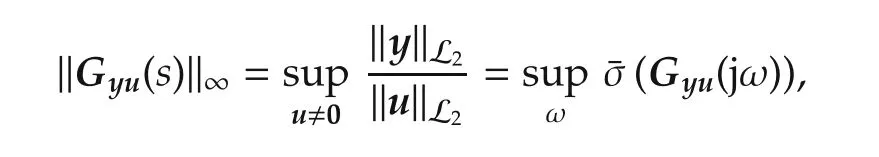
2.2 Graph theory

The communication network of a multi-agent system is modeled by a time-invariant directed graph or digraph,denoted as G=(VG,EG).A vertex i in the set of vertices VGrepresents the ith agent in the network,with|VG|=N∈N.Agent i sends information to agent j if the edge(i,j)∈EGexists.The in-degree din,iof vertex i indicates the number of vertices that send information to vertex i.Accordingly,the in-degree matrix is defined asThe adjacency matrix of the graph is given by AG=[aGij]∈ RN×N,with

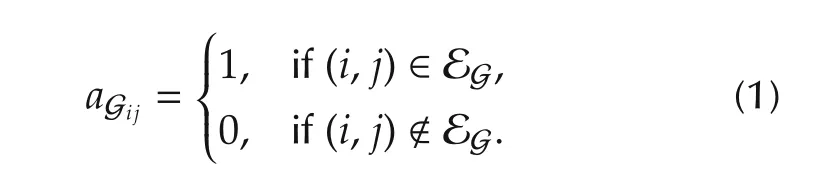
Furthermore,a convenient way for describing the communication network of a multi-agent system is given by the graph Laplacian,which is one of the most important matrices in the context of synchronization problems[1].It is defined aswith

From its definition,it is immediately apparent that0isalways an eigenvalue of LG,since all rows of the Laplacian matrix sum up to zero,i.e.,LG1=0.

The following definition describes a fundamental property of digraphs.

De finition 1A digraphis said to contain a directed spanning tree if there exists at least one vertex–also called root vertex–that can reach every other vertex,using the edges given in the set EG.

Remark 1Coinciding with Definition 1 is the requirement that the Laplacian matrix LGhas a simple eigenvalue in zero[1],i.e.,and λl(LG)≠ 0,for l∈{2,...,N}.

2.3 Problem statement

We consider a heterogeneous multi-agent system consisting of N agents described by the linear timeinvariant dynamics

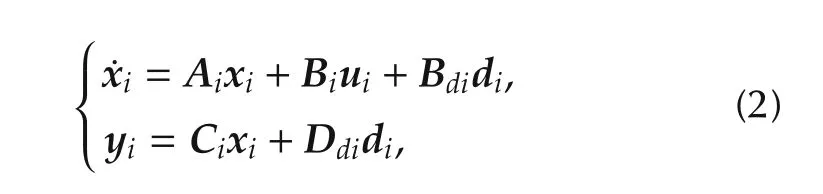
where xi∈Rni,ui∈Rmiand yi∈Rpare the state,control and output vectors of the ith agent,i∈{1,...,N}.The matrices Ai∈ Rni×ni,Bi∈ Rni×miand Ci∈ Rp×niare assumed to be constant and known.Note that the state and input dimensions can be different among the agents,but the output vector of every agent has the same dimension p,since only synchronization of physically comparable outputs makes sense.The vector di∈Rlidescribes arbitrary disturbances,which may be exogenous or result from parametric uncertainties,and it belongs to the space L2[0,∞),meaning that it is limited in its energy.The disturbance vector is unknown,but we assume that we have information about the way how it acts on the system by the matrices Bdi∈ Rni×liand Ddi∈ Rp×li.

Our goal is to find decentralized control laws

such that in the undisturbed case we get

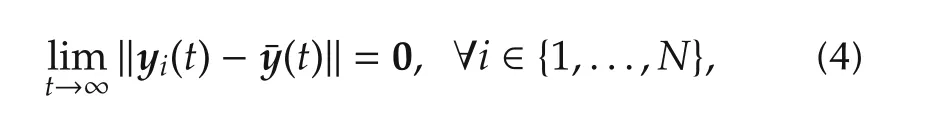
where ηi∈Rpis the new reference input andis the synchronization trajectory which will be defined in the next section.Furthermore,in the disturbed case the influence of the disturbance vector dion the output vector yishould be minimized by means of the H∞norm,i.e.,

Hence,the robust output synchronization problem can be formulated as follows.

Problem 1For a multi-agent system consisting of N heterogeneous agents(2),find distributed controllers(3)such that for the overall system the requirements(4)and(5)are satisfied.

Next,we focus on square systems,meaning that as many actuators as outputs are available for control.Obviously,achieving robustness is more difficult in this case,because less degrees of freedom are available.However,we will point out that there are remaining degrees of freedom which can be used to optimize the robustness of the synchronization process.The results can easily be extended to over-actuated systems,but for reasons of brevity we assume hereafter that mi=p,for all i∈{1,...,N}.

3 A noninteracting control strategy for output synchronization

In this section,we present an input-output decoupling method which,in absence of disturbances(i.e.,di=0),leads to output synchronization for the heterogeneous agents(2).The idea is to homogenize the input-output behavior of the agents,using noninteracting control techniques.Hence,if the same input signal is applied to every agent,their outputs will synchronize.Fig.1 illustrates the controller structure.Using a feedback matrix Kiand a pre-filter matrix Fithe inputoutput behavior from ηito yiwill be homogenized.Furthermore,the reference signals ηiwill be generated by exosystems that can be synchronized by exchanging information through the network.

Fig.1 Controller structure for agent i.The communication of the variables ζiand ζ jis illustrated by connections to the network.

Next,we first describe the method to generate identical reference signals for every agent,before we present the homogenization approach.

3.1 Synchronization of the reference inputs

Similar to the idea presented in[8],identical reference signals can be generated by introducing homogeneous exosystems into every agent and synchronizing these exosystems by standard methods for homogeneous agents.The dynamics of the ith exosystem are described by

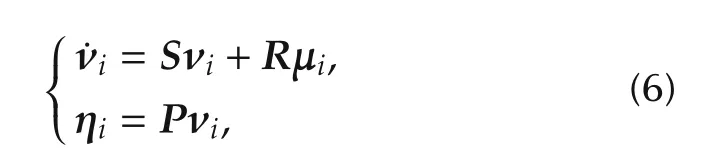
where νi∈ Rsand μi∈ Rrare the state and input vectors and ηi∈ Rpis the generated reference trajectory which is said to be tracked.Note that the matrices S ∈ Rs×s,R ∈ Rs×rand P ∈ Rp×sare identical for all agents and system(6)is assumed to be stabilizable and detectable.The goal is to find a control law μiso that differences between the exosystem outputs vanish and every exosystem produces the same output signal,i.e.,

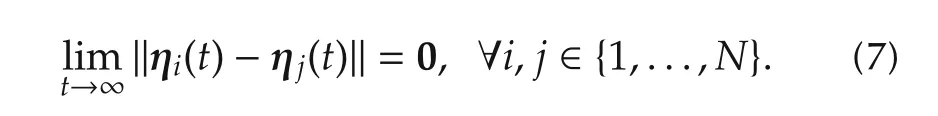
Remark 2For the generation of a non-trivial reference trajectory,we assume that S is anti-stable.If there exist stable eigenmodes in the exosystem,these modes will vanish asymptotically,so that they are negligible.

Equation(7)describes the standard synchronization problem for homogeneous systems.It is well known in the synchronization literature that this problem can be solved by distributed feedback laws

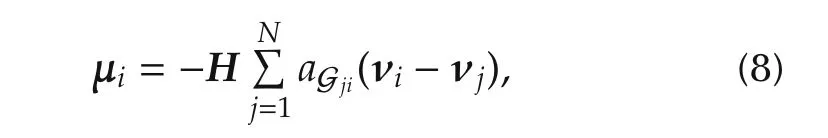
where the parameter aGjiis given as in(1)and the feedback matrix H ∈ Rr×sneeds to be determined such that the exosystems synchronize.Note that the same matrix H is used in the control law(8)for every agent.Hence,with Rr∍ ζl=Hνl,an equivalent representation for control law(8)is given by

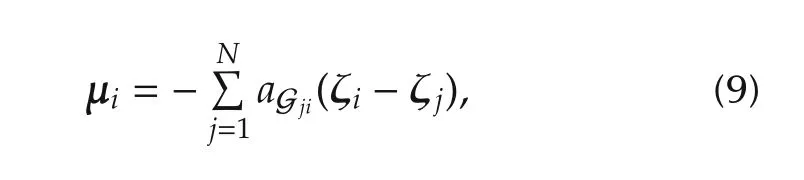
which will be used hereafter.Obviously,both control laws result in the same value for μi.However,(9)hasthe advantage that less information needs to be exchanged through the communication network.While in(8)the exchanged signals have a length of s,in(9)a signal of length r needs to be exchanged.Since usually the input dimension of a system is less than its state dimension,i.e.,r＜s,less information have to be communicated.

From[4],we know that the synchronization task(7)is solved by the distributed control laws(9),if and only if the matrices

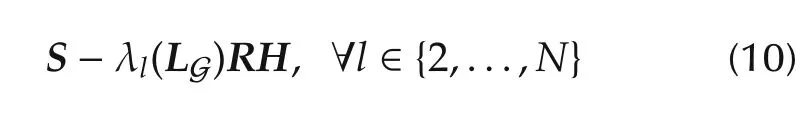
are Hurwitz,where λl(LG)denotes the lth eigenvalue of the Laplacian matrix LG.Note that λ1(LG)=0 is always an eigenvalue of LG(cf.Section 2.2).Thus,the synchronization problem can be reduced to a stabilization problem,where a single matrix H is searched such that the matrices(10)are simultaneously Hurwitz for all l∈{2,...,N}.Furthermore,since S is assumed to be anti-stable,synchronization can only be achieved if the digraph,which describes the communication network,contains a directed spanning tree.According to Remark 1,λ1(LG)=0 is a simple eigenvalue if and only if the digraph contains a directed spanning tree.Otherwise,there exists an l ∈ {2,...,N}with λl(LG)=0 such that(10)can not be made Hurwitz.In[6],an LQR-based method is presented to calculate a matrix H which solves the simultaneous stabilization problem.

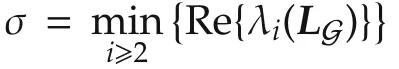
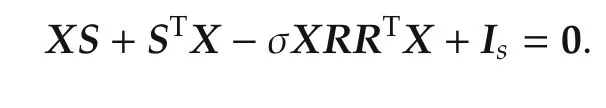
In that case,the exosystem outputs ηiconverge to the trajectorywith

Theorem 1 is a well-known result for the synchronization of homogeneous agents,hence,the proof is omitted and can be found in[6].

After synchronizing the exosystems,the inputs μivanish and every exosystem acts as an autonomous system that produces the same reference signal¯η.In the next section,we presentan approach wherethe input-output behavior of the agents are homogenized,meaning that if we apply the same reference input¯η,then the same output¯y will be produced by every agent.

3.2 Homogenization by input-output decoupling

In the undisturbed case the dynamics of the ith agent read

Following the idea of noninteracting control[18,19],we use a control law

where the matrices Ki∈ Rp×niand Fi∈ Rp×pare determined such that the transfer matrix from ηito yihas a diagonal structure,meaning

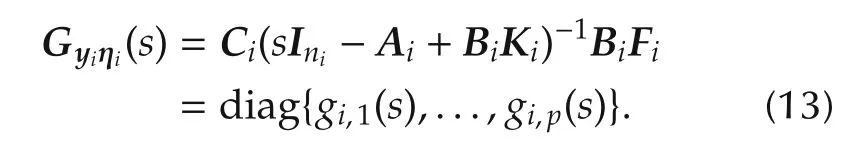
If the closed-loop transfer matrix is given as in(13),every output signal is completely decoupled from the remaining dynamics and can be influenced individually.The transfer functions gi,k(s),k∈{1,...,p},in(13)have the form of simple lag elements

which describe the relationship from the kth input signal ηi,kto the kth output signal yi,kfor agent i.Herein,δi,kis the relative degree of the kth output yi,kand it specifies the order of the lag element(14).The relative degree is a system property which states how often yi,kmust be differentiated with respect to time until it is affected by the input vector ui.It is defined as[18]

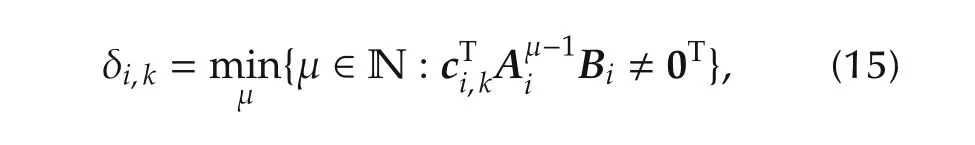
Furthermore,according to[18],we define the decoupling matrix

For achieving stable input-output decoupling with the static control laws(12),the agents have to satisfy the following two assumptions.

Assumption 1The decoupling matrix(16)is invertible,i.e.,

Assumption 2System(11)is minimum phase,meaning it has no invariant zeros in the closed right half of the s-plane.

Remark 3If the above assumptions are unfulfilled,stable input-output decoupling is still possible if a dynamic control law is applied instead of the static controller(12)(cf.[20]).In this article,we assume that Assumptions 1 and 2 are fulfilled for every agent,but the results can be extended to systems where this is not true.This can be done for instance by the method presented in[20].

Theorem 2Given system(11)together with controller(12)and let Assumptions1 and 2 hold.Then,for the feedback and pre-filter matrices Ki=

the closed-loop system for agenti results in the diagonal transfer matrix(13),with transfer functions(14).

ProofConsidering(15),for the kth output signal and its time derivatives,we can write

The corresponding differential equation of transfer function(14)reads

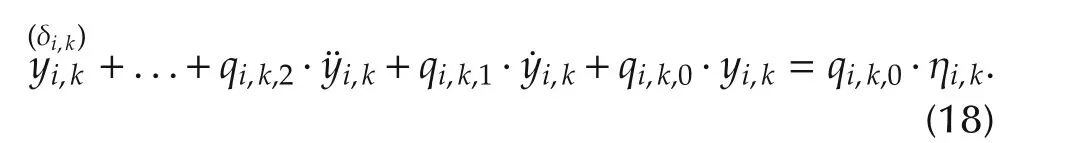
Now,applying(17)to(18)leads to

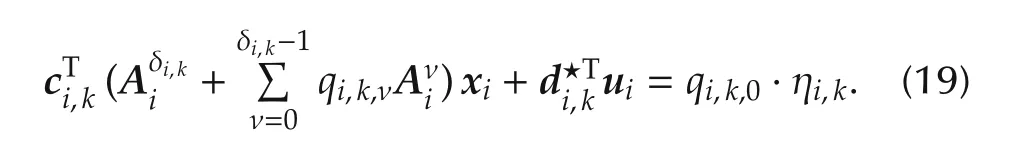
Writing(19)for all k∈{1,...,p}in matrix form,we get

Hence,(20)is fulfilled if the control law is given by

which leads to the closed-loop transfer matrix(13)with transfer functions(14).

If we calculate the matrices Kiand Fias described in Theorem 2,the kth output signal yi,kof agent i follows the kth referenceinput ηi,k,wherethe transient behavior is determined by(14).Hence,choosing the free parameters qi,k,νidentical for all agents and such that(14)is stable,leads to the same transient behavior in the kth channel,i.e.,gi,k(s)=gk(s)for all i∈{1,...,N}.Further,applying the same reference inputfor every agent,the same trajectory will be tracked and output synchronization is achieved.The kth synchronization trajectory is then described bywhere gkdenotes the impulse response

with fi,kbeing the kth column vector of the filter matrix Fi,and the asterisk denotes the convolution operation

Note that the above argument is only true if the relative degree for every agent is the same in the kth channel.However,in heterogeneous networks the agents can exhibit different relative degrees.Therefore,it could be necessary to adjust the relative degrees.

3.3 Adjustment of the relative degrees

Often,the agents in a heterogeneous network are structurally homogeneous and have similar dynamical properties.Forinstance,in a network of different ground vehicles the relationship between the actuators and the output signals are similar,resulting in same relative degrees.However,if we are interested in synchronizing completely different agents with different relative degrees,an adaptation is needed.

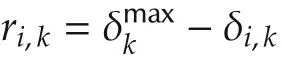
denote the difference of the kth relative degree for the ith agent compared to the maximum relative degree.If the kth relative degree δi,kof agent i is less thanwe include a delay element such that the transfer function from ηi,kto yi,khas the same orderfor all agents.

For this purpose,the parameters qi,k,νof agents with maximum relative degree in the kth channel are determined such that their transfer functions are identical,i.e.,forwe getFor agents witha delay element

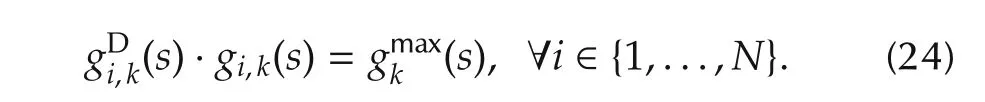
That is,every exosystem signal ηi,kfor which the corresponding output channel has a relative degree δi,k＜must be delayed through a dynamical element(22)with transfer function(23)so that(24)is met.

It should be noted that with the above description it is not always possible to satisfy(24).For instance,suppose thatandFurthermore,suppose that the desired poles forhave a nonzero imaginary part.Then,(24)can only be satisfied if gi,k(s)andboth have one pole with a nonzero imaginary part,resulting in complex valued control laws.However,since it is not possible to implement complex valued control laws,another approach is needed to get the desired input-output behavior in the kth channel.This goal can be achieved in the following way.

This can be achieved if the parameters in the kth row ofare set tofor all ν ∈ {0,...,δi,k− 1}and into qi,k,0=1.Furthermore,the delay element is also set up as an integrator chain of order ri,k,meaning

Together,this results in

A state space model for the integrator chain(27)is

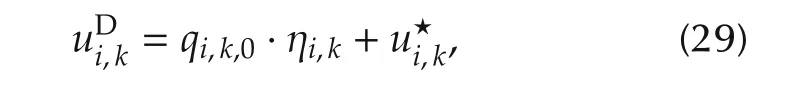
where ηi,kis the kth reference signal from the ith exosystem.Moreover,the signalis given by

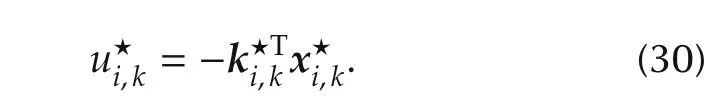
If the feedback gain vector is determined by

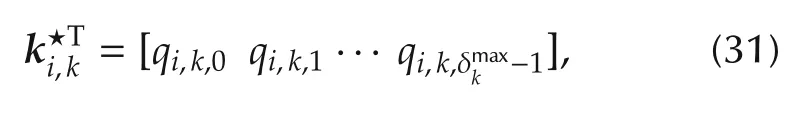
then for an appropriate choice of the parameters qi,k,ν,the transfer function from ηi,kto yi,khas exactly the desired form,which can be verified easily.

The problem of this approach is that we need the unknown state vectorfor the feedback law(30).However,this vector can be generated by a simple state transformation.From(28),the following relationship can be derived:

Furthermore,since the decoupling controller(21)and the delay element(22)are determined such that the input-output behavior fromto yi,kis described by an integrator chain as in(27),it follows that the higher time derivatives are determined by

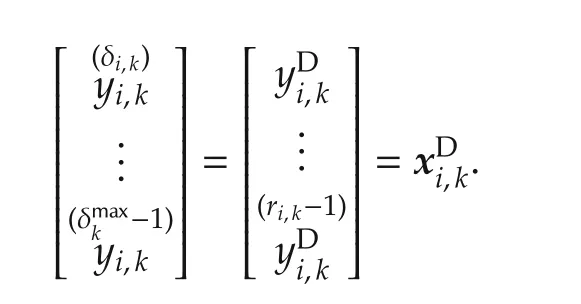
Summarizing the design procedure,we can conclude that if the relative degree δi,kfor the kth output of the ith agent is less than the maximum relative degreethen:

1)include a delay element(22)which describes an integrator chain(26)of order

2)determine the control law(21)such that gi,k(s)describes also an integrator chain as in(25),

3)calculate the state vectoras shown in(32),and

4)determine the input signalof the delay element as given in(29)and(30).

Regardless of whether a delay element is needed or not,the above design steps can be used to describe the free parameters qi,k,νin a more compactform,which will be helpful for the further calculations in the next section.For this purpose,the first two design steps are applied to every input-output channel.Next,we compose the delay elements for every channel to get the overall delay system

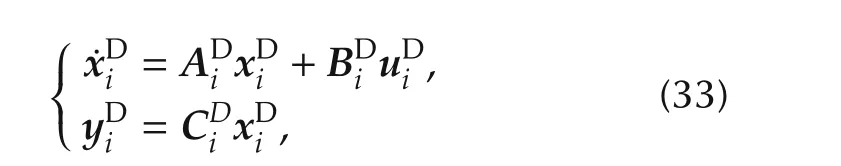
with the matrices

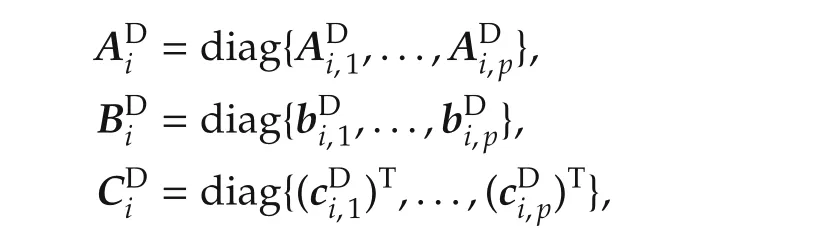
and the stacked vectors

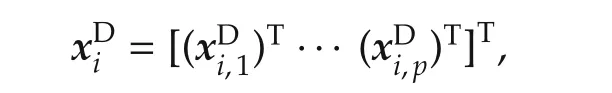
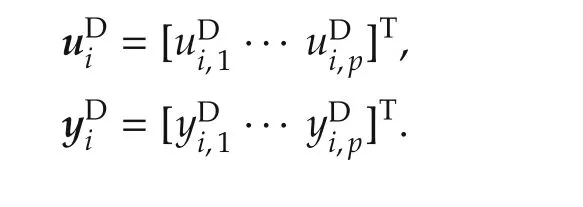
Furthermore,we rewrite(32)as

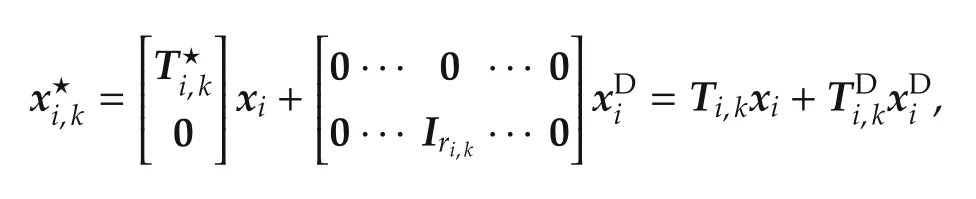
meaning that the lower part offilters out the vectorfrom the overall vectorThen,

can be calculated by

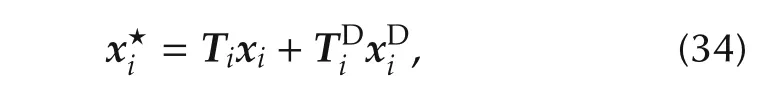
where

with the matrices

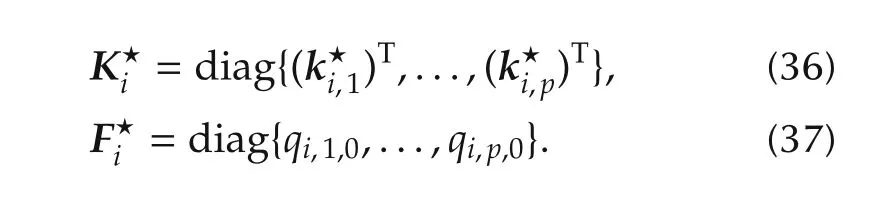
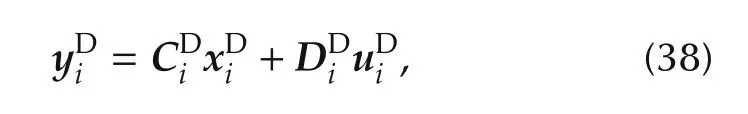
where for the kth channel the delay matrices have to be adapted such that

The advantage of describing the closed-loop system as shown in Fig.2 is that the matricesandhave a special structure and contain only the free parameters qi,k,ν.These parameters can be determined arbitrarily.The only requirement is that for every agent the same parameters are used,to get a homogeneous input-output behavior,and that the resulting transfer matrix from ηito yiis asymptotically stable.Hereinafter,we present a method to specify the free parameters in a way such that the robustness of the synchronization process is increased.

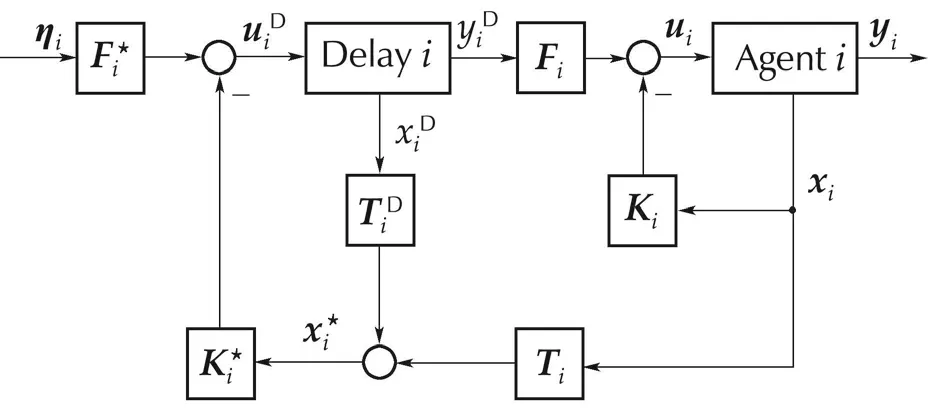
Fig.2 Extended control structure for agent i,with delay element for the adaptation of the relative degrees.

4 Robust input-output decoupling

The presented solution to the output synchronization problem consists of two parts.Synchronizing identical exosystems and homogenizing the input-output behavior by noninteracting control techniques.By this procedure,the synchronization task is separated from the agent dynamics.That is,the robustness issue reduces to a robust input-output decoupling task.

4.1 Agents without delay element

We consider again the disturbed agents

Furthermore,we first assume that the agents have identical relative degrees in every input-output channel,meaning that δi,k= δk,for all i ∈ {1,...,N}and k∈{1,...,p}.Hence,no delay element is needed and the control law for achieving input-output decoupling is given by

The input-output behavior of the agents are homoge-nized if the parameters qi,k,ν,and thus the transfer functions(14),are identical for every agent,i.e.,qi,k,ν=qk,ν.However,the parameters qk,νare determined by the designer and,therefore,provide some degrees of freedom which can be used to minimize the influence of the disturbances on the agents(39).Considering the input-output decoupling requirement,the following optimization problem can be formulated:

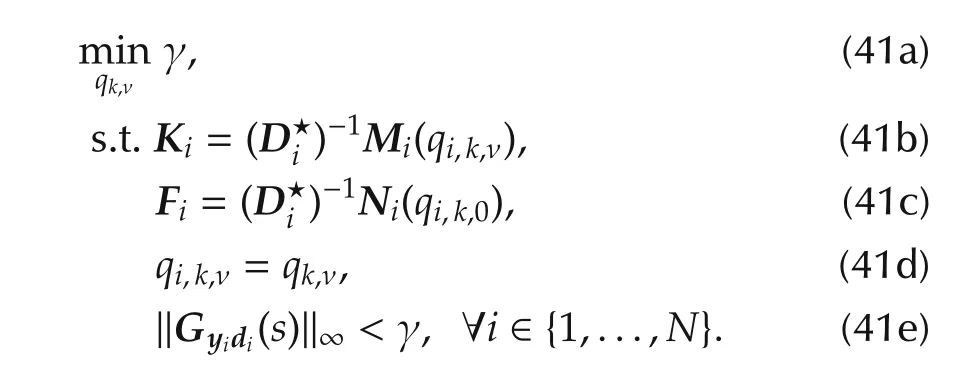
Due to conditions(41b)and(41c),this is a structurally constrained optimization problem and,hence,nonconvex.Next,we deduce a methodology for satisfying conditions(41b)and(41c)by reformulating(41)as a standard control problem and using solvers like HIFOO[16,17],which has been designed for such structurally constrained problems.Beyond that,we use the special capability of HIFOO to simultaneously find one optimized controller for several plants.This allows to satisfy conditions(41d)and(41e)by optimizing one set of parameters qk,ν,which maximizes the disturbance attenuation for all agents.

The structure of the standard control problem with generalized plant Piand controller Kiis depicted in Fig.3 and can be formulated as

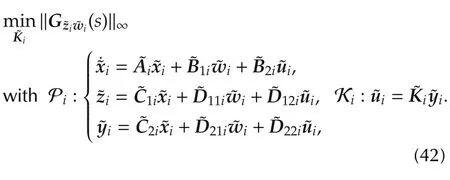
Stacking the inputs diand ηitogether to the generalized inputand withx˜i=xi,the matrices for the ith generalized agent read

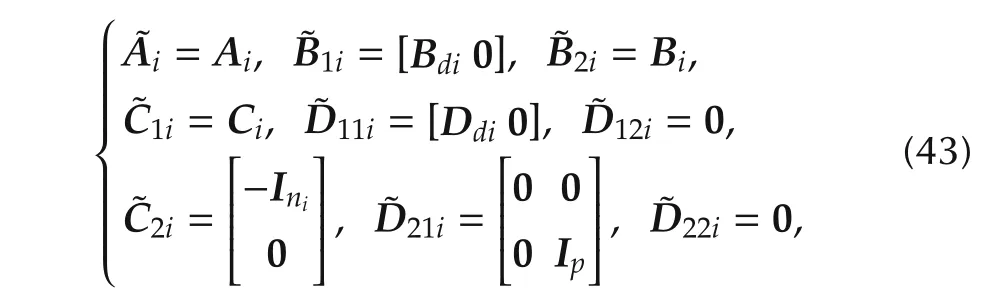
with performance output˜zi=yi.The generalized controller for the above system is then

Fig.3 Structure of the standard control problem.

This formulation implies that a controller˜Kiis searched which stabilizes system(42)and simultaneously minimizesNote that the influence of ηion yiis totally determined by the input-output decoupling requirement,thus,the minimization ofis equivalent to the minimization of.However,with the system description(42)–(44)the structural constraints for the matrices Kiand Fi,which are imposed by(41b)and(41c),are not met.Since we want to achieve an input-output decoupling,the matrices Kiand Fimust match the structural constraints given by(41b)and(41c),which is not fulfilled for system(42)–(44).In the standard control problem,structural constraints in the generalized controller are considered as zero elements.Hence,it is necessary to reformulate the generalized plant matrices(43)and controller(44)such that the structural constraints are met.

For this purpose,we first decompose the feedback matrixinto

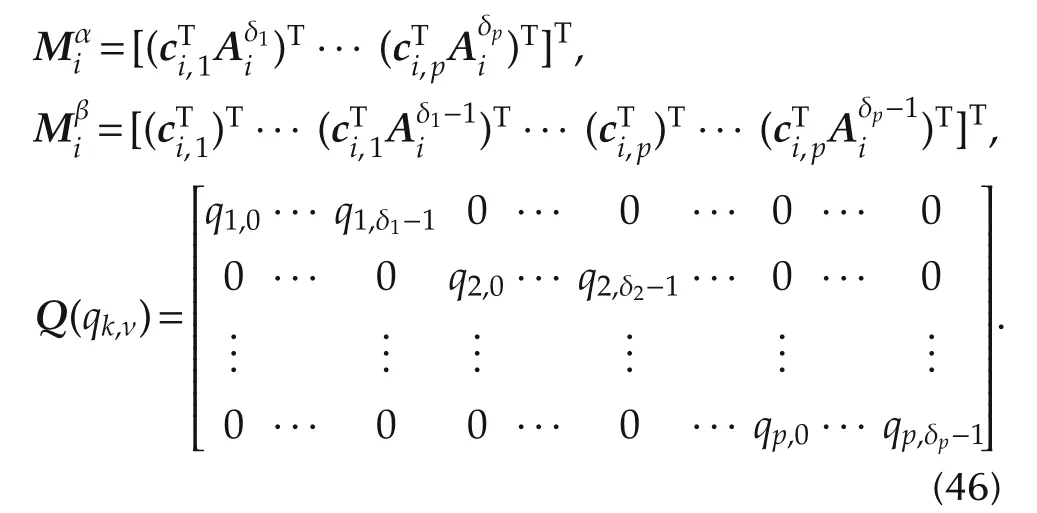
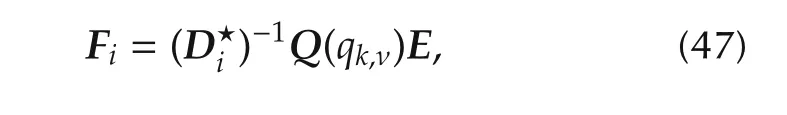
Theorem 3Given that for agent i no delay element is needed.Then,an equivalent formulation for optimization problem(41)is the standard control problem(42),with the N generalized plants

where the generalized controller is given by

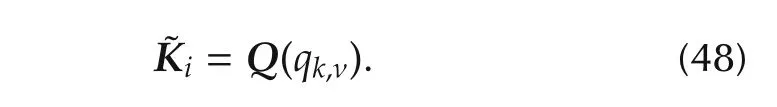
ProofTaking(45)and(47)into account,the closedloop system(39)and(40)can be written as

Thus,a simple comparison with the generalized plant matrices in Theorem 3 proves the claim.

Theorem 3 illustrates the benefit of reformulating the robust input-output decoupling problem as a structural constrained standard control problem.Since the generalized plant matrices depend on the matrices of the ith agent,a single controller is sought which simultaneously stabilizes all agents and minimizes‖G˜zi˜wi(s)‖∞and ‖Gyidi(s)‖∞respectively.That is exactly what the solver HIFOO was designed for.As a result,we obtain an input-output decoupling as in(13),where the transfer functions(14)in the kth channel are identical for all agents and where the parameters qk,νare optimized such that the multi-agent system is robust against disturbances.

4.2 Agents with delay element

Theorem 3 provides a way for reformulating the optimization problem(41)as standard control problem(42)for agents where every input-output channel has maximum relative degree,i.e.,If one channel of agent i has a relative degree witha delay is needed and a formulation of the standard control problem as in Theorem 3 is not possible.

According to Section 3.3,we can extend the control structure as shown in Fig.2 to adjust the relative degree in every input-output channel.For this purpose,we combine the agent dynamics(39)with the delay system(33),where its output equation is given by(38).Additionally,considering that the input vector of the agent is determined bywe can write

Here,the matrices Kiand Fihave been calculated such that input-output decoupling is achieved,where every channel fromto yiis described by an integrator chain.

Furthermore,with(34)and(35),the input vectorcan be written as

Note that we have left out the subscript i for the matrices K⋆and F⋆,since they have to be identical for every agent.Comparing the feedback matrix K⋆with the parameter matrix Q(qk,ν),it is apparent from(31),(36)and(46)thatMoreover,sinceit follows from(47)that F⋆=Q(qk,ν)E.Hence,definingas before,the standard control problem for agents with delay element can be formulated asin(42),with generalizedplant matrices

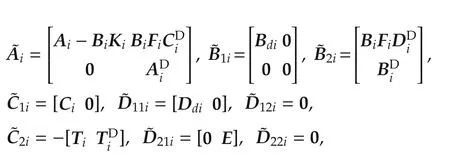
Describing the standard control problem as shown in this section,an alternative way is provided for solving the optimization problem(41)for agents that have to adjust their relative degree.This alternative way can also be applied to agents that do not need a delay element.Then,the delay element is a direct feed through,meaning thatand that there is no state vectorIn that case,the effect ofand its corresponding matrices must be eliminated from the above description.However,it should be noted that this alternative solution relies on an inner feedback law to generate input-output decoupled integrator chains in every channel and an outer feedback law to get the desired transfer functions with the optimized parameters.Hence,the computational cost for this method is increased compared to the solution presented in Section 4.1.

Remark 4With the given alternative solution,it is also possible to include additional delay elements for the agents,even if they do not need them for the adjustment of their relative degrees.By doing so,we get additional parameters qk,νresulting in more degrees of freedom for the optimization.

4.3 Parameter restriction and further optimization

With the proposed methods,it is possible to optimize the free parameters qk,νsuch that the robustness of the synchronization process is increased.However,it should be noted that the optimization parameters are unrestricted.Hence,the optimization process can lead to arbitrary or unwanted values for qk,ν.For this reason,next,we show a method to restrict the possible values for qk,νand present also a way for a further optimization of the closed-loop systems.

First,the N generalized plants can be extended by two additional plants to ensure that the polesof the kth transfer function(14)lie in a specified region satisfying

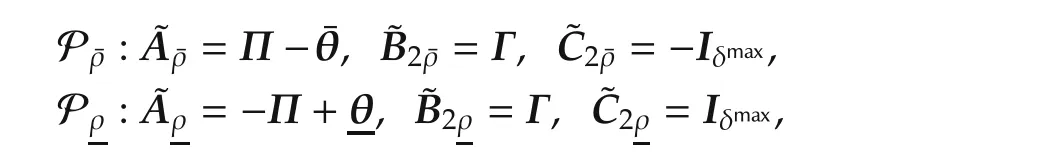
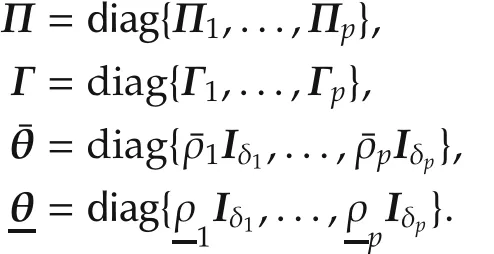
All other generalized plant matrices are set to 0.Note that the plants are denoted as virtual because they are only introduced for the controller computation.The generalized plant P¯ρensures that all poles of the kth transfer function have a real part smaller thanThis gets obvious if we consider the closed-loop plant P¯ρwith controller(48),leading to

The bracketed expression is nothing but the state-space description of transfer matrix(13),where the transfer functions(14)are represented in controllable canonical form.Since the generalized controller Q(qk,ν)makes the matrix(51)Hurwitz,it is ensured that the poles of the kth transfer function are on the left side of the given bound¯ρk.Similarly,the closed-loop plant for Pρleads to

Hence,since the matrix(52)is also Hurwitz,the closedloop poles of the kth transfer function are on the right side of the bound given by ρk.Since the same controller(48)is applied to all plants,P¯ρand Pρensure that(50)is satisfied for all agents.

So far,we have scheduled that the transfer functions(14)must have a static gain of gi,k(s=0)=1.However,this is only necessary if we want to track the reference signal exactly with the same amplitude.If the tracking behavior does not need to have a static gain of 1,the transfer function in the kth channel can be rewritten as

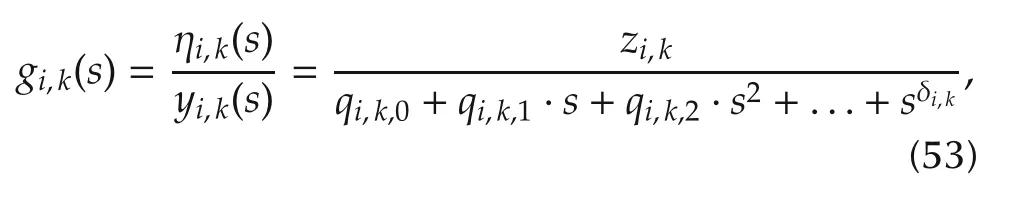
with the free parameter zi,k.Obviously,if we fix zi,k=qi,k,0this leads to a static gain of 1,but if we allow other static gains,it is possible to use this parameter for a further optimization.Hence,we extend problem(41)by

Then,the pre-filter matrix changes toand the generalized plant matrices in Theorem3become

with all other matrices unchanged.The generalized controller then reads

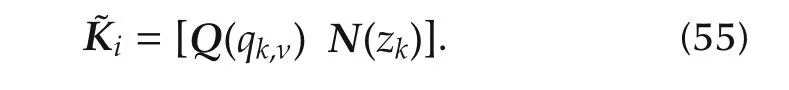
Equivalently,for the solution described in Section 4.2,we have to change the generalized plant matrices as

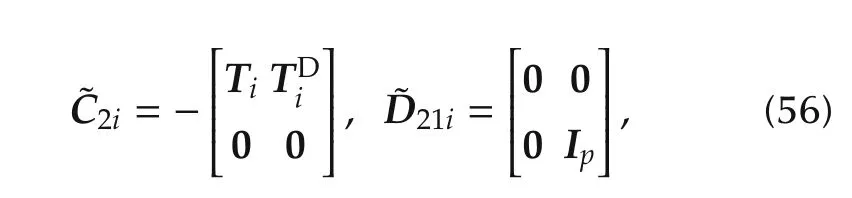
with all other matrices unchanged.This extension provides additional degrees of freedom in the parameters zk.Note that in that case it is also necessary to change the output matrices for the generalized plants P¯ρandto

Controller(55)might result in very small values for zk,due to the objective of minimizing.To overcome this problem and to ensure a minimum static gain ξk＞ 0,we introduce a further generalized virtual plant

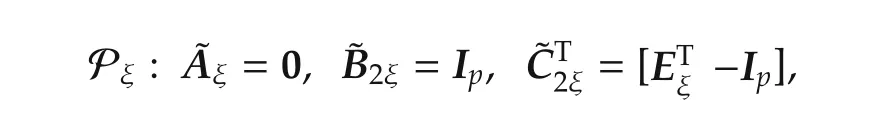
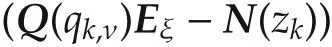
is Hurwitz,which implies that the requirements zk＞ξk·qk,0are satisfied.

Theorem 4Extending the N generalized plants in Theorem 3 by the three additional plants P¯ρ,Pρand Pξ,and replacing the generalized plant matrices by(57)and(54)or(56),the new generalized controller(55)leads to transfer functions(53).Moreover,the poles of this transfer functions lie in the region described by(50)and a minimum static gain of gi,k(s=0)＞ ξkis guaranteed.

Remark 5Itis also possible to restrict the static gain to a maximum value if we introduce a further generalized plant.However,since we are interested in the minimization of the H∞norm from dito yi,the parameters zkwill tend to small values,rather than large values.Therefore,an upper bound for the static gain is not necessary.

5 Example

To demonstrate the effectiveness of the presented approach,we want to synchronize the sideslip and roll angles of a heterogeneous fleet of N=3 different types of aircraft,namely a Grumman X29-A(FSW)[21],aBoeing-767[22]and a Lockheed L-1011 TriStar[23].The system and input matrices of the agents are given by

which describe the linearized lateral dynamics in cruise flight.The state and input vectors for every agent are given byHerein,the variables denote the sideslip angle βi,roll angle Φi,roll rate pi,yaw rate ri,aileron deflectionand rudder deflection,for all i∈{1,2,3}.Since we aim to synchronize the sideslip and roll angles,the output matrix for every agent reads

We assume that the communication network is given by a ring topology.The corresponding graph and the Laplacian matrix are shown in Fig.4.

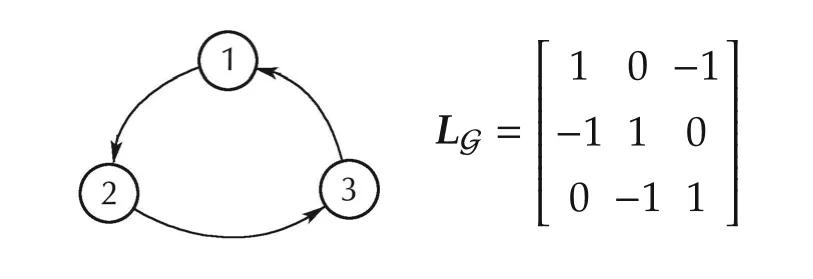
Fig.4 Communication network and corresponding Laplacian matrix.

Furthermore,we assume that the agents are disturbed by exogenous signalsφi)),where n(t)is a white gaussian noise with power 1 and αi∈ [0.4,0.5].Vi∈ [−0.15,0.15]is a constant disturbance and the parameters of the sinusoidal signal areandThe disturbance matrices are given by Bdi=1 and Ddi=1 for every agent.

Our goal is to synchronize the agents’outputs to predefined trajectories,where we use a ramp function for the sideslip angles and a harmonic oscillation for the roll angles as synchronization trajectories.Thus,for generating the reference signals,we introduce exosystems with the system matrices

For the agents,we can see that Assumptions 1 and 2 are fulfilled and the relative degrees are δi,1=1 and δi,2=2 for all i∈ {1,2,3}.That is,the design of noninteracting controllers leads to first order lag elements in the first input-output channel and second order lag elements in the second input-output channel.

First,we have designed input-output decoupling controllers,where the poles for every transfer function gi,k(s)are placed at−1.This results in an initial upper bound of γin it=6.42 for the H∞norms of‖Gyidi(s)‖.Fig.5 shows the simulation results for this case.Obviously,for the initial controllers the sideslip and roll angles are highly disturbed and synchronization is not obtained satisfactorily.

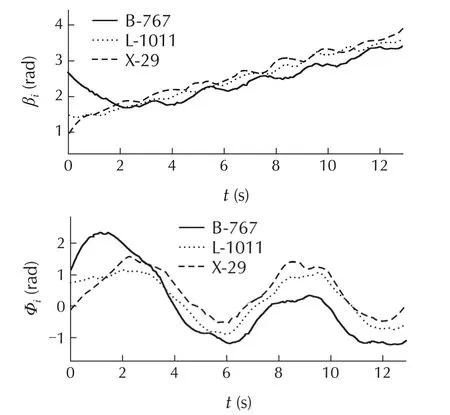
Fig.5 Sideslip(βi)and roll(Φi)angles of the B-767,L-1011 and X-29,with initial controllers.

Next,we have optimized the solution as described in Section 4.1.Therefor,we have restricted the eigenvalues of the transfer functions as shown in(50),with¯ρk=−0.5 andfor both channels.In addition,we have also optimized the parameters zkconsidering a minimum static gain of gi,k(s=0)＞ ξk,with ξ1=0.9 and ξ2=0.8.The result of this optimization process leads to H∞norms of less than γopt=2.13.That is,the disturbance impact is reduced by nearly 67%.Fig.6 shows the simulation results,which demonstrate the effectiveness of the proposed methodology.Compared to the initial solution,a good disturbance attenuation is achieved and the synchronization process works well.

Fig.6 Sideslip(βi)and roll(Φi)angles of the B-767,L-1011 and X-29,with optimized controllers.

5.1 Different relative degrees

Now,we consider a further example,where it is assumed that the input matrix of the Grumman is modified as

Thus,the relative degree in the first input-output channel for this agent changes to δX-29,1=2.That means that for the Boeing and the Lockheed a delay element of order 1 needs to be included in the first input-output channel to adjust their relative degrees,as described in Section 3.3.Moreover,for reformulating the optimization problem into the standard control problem framework,the solution described in Section 4.2 is applied.Since the Grumman has maximum relative degree in both channels,the optimization problem for this agent is still described as shown in Section 4.1.Solving the synchronization and the optimization problem with the same constraints as before,we get an optimized H∞norm of

Despite the fact that the robust synchronization task is also satisfied for this modified case,we can see that the disturbance attenuation is slightly improved.According to Remark 4,this improvement comes from the additional optimization parameter in the first input-output channel.Since the synchronization process for this case looks similar to the solution shown in Fig.6,the simulation results are omitted.

6 Conclusion

In this article,we have proposes a new method for solving the robust output synchronization problem for networks of heterogeneous agents.Using the theory of noninteracting control,the dynamics of the agents can be homogenized by a simple input-output decoupling strategy.Hence,applying the same reference input,which is generated by identical exosystems,results in synchronization.Moreover,we have shown that the presented approach provides some degrees of freedom which can be used to increase the robustness of the agents against exogenous disturbances by a proper choice of the controller parameters.Reformulating the problem as a standard control problem,the disturbance attenuation of the agents can be optimized by simple optimization methods.The effectiveness of the approach has been shown for the synchronization of the roll and sideslip angles of a heterogeneous aircraft fleet.

Future work is required to extend the results to systems that are not input-output decouplable by static controllers.In that case dynamically extended control laws can be applied to overcome this problem.

[1]R.Olfati-Saber,J.A.Fax,R.M.Murray.Consensus and cooperation in networked multi-agent systems.Proceedings of the IEEE,2007,95(1):215–233.

[2]W.Ren,R.W.Beard,E.M.Atkins.Information consensus in multivehicle cooperative control.IEEE Control Systems Magazine,2007,27(2):71–82.

[3]J.A.Fax,R.M.Murray.Information flow and cooperative control of vehicle formations.IEEE Transactions on Automatic Control,2004,49(9):1465–1476.

[4] C.Ma,J.Zhang.Necessary and sufficient conditions for consensusability of linear multi-agent systems.IEEE Transactions on Automatic Control,2010,55(5):1263–1268.

[5] L.Scardovi,R.Sepulchre.Synchronization in networks of identical linear systems.Automatica,2009,45(11):2557–2562.

[6] S.E.Tuna.LQR-based coupling gain for synchronization of linear systems.2008:http://arxiv.org/pdf/0801.3390.pdf.

[7]H.Kim,H.Shim,J.H.Seo.Output consensus of heterogeneous uncertain linear multi-agent systems.IEEE Transactions on Automatic Control,2011,56(1):200–206.

[8]P.Wieland,R.Sepulchre,F.Allgöwer.An internal modelprinciple is necessary and sufficient for linear output synchronization.Automatica,2011,47(5):1068–1074.

[9]B.A.Francis,W.M.Wonham.The internal model principle of control theory.Automatica,1976,12(5):457–465.

[10]P.Lin,Y.Jia,L.Li.Distributed robust consensus control in directed networks of agents with time-delay.Systems&Control Letters,2008,57(8):643–653.

[11]X.Wang,P.Yi,Y.Hong.Dynamic optimization for multiagent systems with external disturbances.Control Theory and Technology,2014,12(2):132–138.

[12]Z.Li,Z.Duan,G.Chen.On H∞and H2performance regions of multi-agent systems.Automatica,2011,47(4):797–803.

[13]Z.Li,Z.Duan,G.Chen,et al.Consensus of multiagent systems and synchronization of complex networks:a unified viewpoint.IEEE Transactions on Circuits and Systems–I:Regular Papers,2010,57(1):213–224.

[14]X.Wang,Y.Hong,J.Huang,et al.A distributed control approach to a robust output regulation problem for multi-agent linear systems.IEEE Transactions on Automatic Control,2010,55(12):2891–2895.

[15]S.Khodaverdian,J.Adamy.Robust output synchronization for heterogeneous multi-agent systems based on input-output decoupling.IEEE International Conference on Control and Automation.Taiwan:IEEE,2014:607–613.

[16]D.Arzelier,G.Deaconu,S.Gumussoy,etal.H2for HIFOO.International Conference on Control and Optimization with Industrial Applications.Ankara,Turkey,2011:http://cs.nyu.edu/overton/software/hifoo/.

[17]S.Gumussoy,D.Henrion,M.Millstone,et al.Multiobjective robust control with HIFOO 2.0.Proceedings of the IFAC Symposium on Robust Control Design.Haifa,Israel,2009:144–149.

[18]P.L.Falb,W.Wolovich.Decoupling in the design and synthesis of multivariable control systems.IEEE Transactions on Automatic Control,1967,12(6):651–659.

[19]B.S.Morgan.The synthesis of linear multivariable systems by state-variable feedback.IEEE Transactions on Automatic Control,1964,9(4):405–411.

[20]B.Lohmann.Vollst¨andige Entkopplungdurchdynamische Zustandsr¨uckf¨uhrung.at-Automatisierungstechnik,1991,39(9):459–464.

[21]J.T.Bosworth.Linearized aerodynamic and control law models of the X-29A airplane and comparison with flight data.NASA Technical Memorandum 4356,1992.

[22]T.I.Fossen.Mathematical Models for Control of Aircraft and Satellites.3rd ed.Norway:Norwegian University of Science and Technology,2013:http://www.itk.ntnu.no/fag/gnc/pensum.htm.

[23]C.Edwards,S.K.Spurgeon.On the developmentof discontinuous observers.International Journal of Control,1994,59(5):1211–1229.

12 June 2014;revised 10 July 2014;accepted 10 July 2014

DOI10.1007/s11768-014-4081-3

†Corresponding author.

E-mail:khodaver@rmr.tu-darmstadt.de.Tel.:+49 6151/16-76053;fax:+49 6151/16-2507.

This work was supported by the German Research Foundation(DFG)within the GRK 1362“Cooperative,Adaptive and Responsive Monitoring of Mixed Mode Environments”(www.gkmm.de).

©2014 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg

Saman KHODAVERDIANreceivedtheB.S.and M.S.degrees in Industrial Engineering from the Technische Universit¨at Darmstadt,Darmstadt,Germany,in 2011 and 2013,respectively.He holds a fellowship of the German Research Foundation(DFG)and is currently working toward the Ph.D.degree with the Control Methods and Robotics Lab of the Technische Universit¨at Darmstadt.His research interests include multi-agent systems,distributed control and optimization,and robust and decentralized control methods.E-mail:khodaver@rmr.tu-darmstadt.de.

J¨urgen ADAMYreceived the Diploma degree in Electrical Engineering in 1987 and the Ph.D.degree in Control Theory in 1991 from the University of Dortmund,Dortmund,Germany.From 1991 to 1998,he worked as a Research Engineer and later as a Research Manager at the Siemens Research Center,Erlangen,Germany.Since 1998,he has been a Professor at the Technische Universit¨at Darmstadt,Darmstadt,Germany,where he is currently the Head of the Control Methods and Robotics Lab.E-mail:jadamy@rmr.tu-darmstadt.de.