储层岩石物理参数对地震参数的影响分析
肖风凯 王茂均 粟亮 曾铭 刘悦
(成都理工大学,四川成都 610059)
储层岩石物理参数对地震参数的影响分析
肖风凯 王茂均 粟亮 曾铭 刘悦
(成都理工大学,四川成都 610059)
储层流体研究对于地震勘探有着十分重要的意义。本文利用经典的Boit- Gassmann方程, 在孔隙度不同的条件下, 通过对目的层进行不同成分的流体替代, 研究了孔隙度、饱和度以及流体成分等岩石物理参数对等效岩石的纵横波速度、密度等地震参数的影响, 并对计算结果的变化规律进行分析。正研究结果表明:含气饱和度的变化使混合流体的可压缩性发生改变, P波速度随含气饱和度的增加先急剧下降,而后转为缓慢升高;孔隙度的变化对P波速度、S波速度和介质密度的影响要大于含油、含气饱和度变化的影响;当目标层充填的流体由气变为油、水时, 目标层的地震响应的AVO 现象变得不明显, 并且随着目标层厚度的逐渐减少, 地震响应产生调谐效应。
Gassmann方程 流体置换 AVO正演 饱和度 孔隙度 薄层 调谐效应
1 储层地质模型
假设地质模型为三个水平层状介质。选择第二层为目标层,进行流体替代, 利用计算结果对纵横波速度、密度的变化规律进行分析。然后改变目标层的厚度和流体成分, 正演合成地震记录, 分析流体以及厚度对AVO 地震响应的影响。
1.1 地层模型参数
第一层为800m厚层泥岩,层参数:

图2

第二层为目标层(流体替换层)为薄层砂岩;
第三层为半无限泥岩空间,层参数:

1.2 孔隙流体参数
水、油、气三种流体进行流体替代,水的密度为1.0g/cm3,体积模量为2.2GPa;气的密度为0.14g/cm3,体积模量为0.02GPa;油的密度为0.8g/cm3,体积模量为1.0GPa。
2 流体置换的理论基础--Gassmann方程
Gassmann方程是岩石弹性物理研究的重要理论工具,它建立了岩石物性参数与地震弹性参数进行沟通的桥梁,并为进一步利用地震信息划分岩性、检测油气提供了理论依据。
Gassmann方程的假设:(1)岩石(基质和骨架)宏观上是均匀、各向同性、完全弹性的;(2)所有孔隙都是连通的;(3)孔隙内部充满无摩擦的流体(液体、气体和混合物);(4)岩石—流体是封闭系统(不排液);(5)当岩石被地震波激励时,流体和骨架之间没有相对运动;(6)孔隙流体对骨架无软化或硬化作用。
在均匀各向同性介质中,流体饱和的多孔介质的纵波速度 vp
和横波速度 vs可以写成:

图3
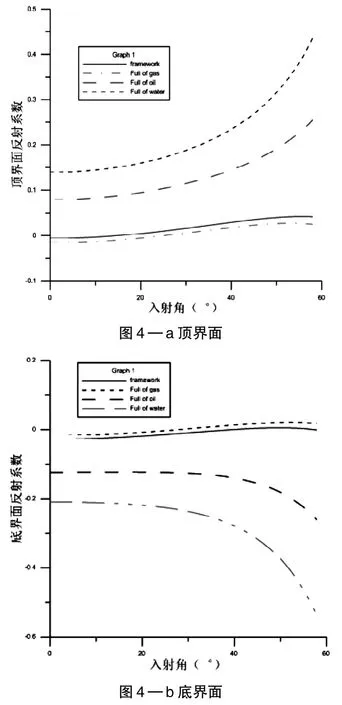
图4 充填不同流体对顶、底界面反射系数的影响
在已知岩石矿物成分和孔隙流体的组成的情况下,本文目标层砂岩的基本参数设为:μm—岩石基质剪切模量,GPa;
采用Nur等人1991年提出的经验公式估算 Kd, μd;为砂岩的临孔隙度值为0.4;
混合流体体积模量 Kf可以用WOOD方程:
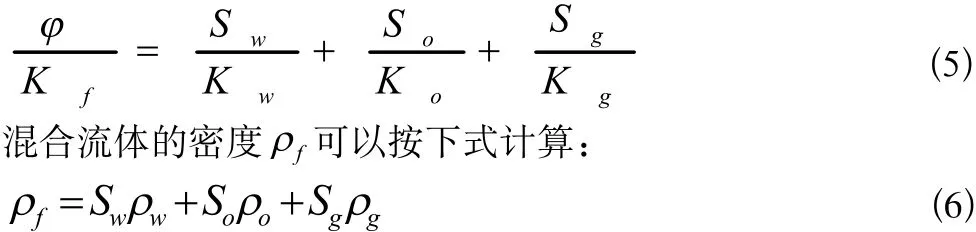
3 流体置换模拟结果分析
3.1 流体成分、孔隙度和饱和度对地震参数的影响
选定第二层为目标层,根据Biot-Gassmann理论,对它进行流体替代, 建立水-气,水-油,油-气混合流体替代模型分析储层孔隙度、流体饱和度变化对纵横波速度,以及等效介质密度的影响情况。假设替代层的孔隙度分别为φ=20%,25%,30%,水的密度为1.0g/cm3,体积模量为2.2GPa;气的密度为0.14g/cm3,体积模量为0.02GPa;油的密度为0.8g/cm3,体积模量为1.0GPa[2]。如图1、2、3。
不含气的情况下,图1中含油饱和度从0~100%,纵波速度平滑递减,从三种孔隙度纵波速度曲线可以看出岩石孔隙度越小速度越大,这与实际情况相符,孔隙度越小,岩石越“实”,纵波速度越大;混合流体体积模量随含油饱和度的增加递减,这是由于油的体积模量小于水的体积模量,当含油饱和度增加时混合流体的体积弹性模量减小;混合流体密度平滑递减。

表1 流体替代参数表
在不含油的情况下,图2中含气饱和度从0~100%,纵波速度先陡然下降,然后再平滑缓慢上升,上升幅度很小,从三种孔隙度纵波速度曲线可以看出岩石孔隙度越小速度越大;混合流体体积模量在流体中含有气体的时候陡然从2.2下降到0.35,然后再随含气饱和度的增加缓慢下降;混合流体密度随含气饱和度增加递减,其递减幅度略大于混合流体体积模量。
在不含水的情况下,图3中含气饱和度从0~100%,纵波速度先陡然下降,下降幅度比水—气模型小,然后再平滑缓慢上升,上升幅度很小,从三种孔隙度纵波曲线可以看出岩石孔隙度越小速度越大;混合流体体积模量在流体中含有气体的时候陡然从1下降到0.35,然后再随含气饱和度的缓慢下降;混合流体密度递减,其递减幅度略大于混合流体体积模量。
结论:①一般认为流体内没有剪切波,流体的孔隙度和饱和度的变化对横波的影响不是很大,所以流体只是通过密度的变化影响横波速度。②同时流体中含气对等效介质的纵波速度影响很大。③但是随着含气饱和度的逐渐增加, 等效介质的纵波速度变化不大。所以,只能确定混合流体相中含气体,但不能确定含气量。因此,地层充填水气混合流体和油气混合流体时的等效速度都和地层完全饱含气时的等效速度相当,在AVO地震响应上差别不明显。
3.2 流体和地层厚度对地震响应的影响
3.2.1 AVO技术基础
本文中采用依赖于角度的Zoeppritz线性近似常规方程:(7)式中:
α、β、ρ分别为上下层的平均速度、密度;Δα、Δβ、Δρ 分别为上下层速度、密度差。
3.2.2 流体置换模型
下面讨论的模型都是在目标层孔隙度为20%的情况下进行的。表1是目标层含水、含油、含气饱和度分别为100%时,计算出来的等效介质的纵横波速度、密度(如表1)。
图4—a中,目的层饱含油砂岩以及饱含水的砂岩声阻抗大于围岩的阻抗,随着入射角的增加反射振幅逐渐增强;饱含气的砂岩以及干骨架的砂岩,振幅随入射角的增加先减小后增大,在入射角为20时出现极性反转现象[4];
图4—b中,目的层饱含油砂岩以及饱含水的砂岩声阻抗小于围岩的阻抗,那么随着入射角的增加反射振幅逐渐增强。
为了更加全面的观测流体和厚度对地震响应的影响,利用表1中的模型数据,对目标层进行流体替代,选用35Hz的雷克子波,采样间隔为0.002s,合成地震记录。为了观测薄层AVO现象,正演模拟中改变目标层的厚度,合成地震记录。
由合成记录可知,目标层在含气和含油的情况下,地震记录很相似, 但是含油时地震反射比含水时的低;目标层含气时,随着目标层厚度的减少,地震记录出现反向;并且目的层含水时的底界面的反射时间比含油和含气时底界面的反射时间提前,这是由于气、油、水三种流体的体积模量是逐渐增加的,从而引起砂岩速度的增加,使得地震波传播时间超前。分别对比充填不同流体时厚度对地震响应的影响:随着厚度的减少,地震响应产生调谐效应,当地层厚度小于地震分辨率时,反射振幅与厚度有关,即其顶和底的反射会产生干涉叠加效应。由于目标层饱含水和饱含油的等效速度大于上下层界面的速度,所以在目标层的上下界面形成反极性反射,随着目标层厚度的减少,顶界面的反射振幅先增加后减少,并且当目标层的厚度小于地震分辨率时,地层厚度与反射振幅成近似的比例关系;当目标层饱含气时,目标层的上下界面形成同极性反射,随着地层厚度的减少顶界面反射振幅增加。
4 结语
基于薄储层地震反射模型,应用Gassmann流体置换方程分析了薄砂岩储层流体饱和度和孔隙度变化对砂岩物性参数的影响;通过AVO正演模拟技术,分析厚度与流体对AVO地震响应的影响,总结出不同流体饱和情况下的地震响应特征,建立岩石流体性质和地震响应特征的联系,这是进行AVO分析的基础。得到以下认识:(1)P波速度随含油饱和度的增加而降低,对含气饱和度的增加先急剧降低后缓慢增加;S波速度随含油和含气饱和度的增加呈线性增加趋势;介质密度随含油和含气饱和度的增加线性降低;P波速度、S波速度和介质密度随孔隙度的增加线性降低,降低程度大于随流体饱和度变化时的情形。(2)目标层在饱含水和饱含油的情况下,PP波的反射系数变化相似,在0到59范围内,反射振幅都随着入射角的增大而增大,但是含油时地震反射比含水时的低。同样目标层在饱含气与干骨架的情况下,PP波的反射系数变化相似,都出现了极性反转现象。(3)当目标层充填的流体由气变油和水时,目标层的地震响应的AVO现象变得不明显,并且随着目标层厚度的逐渐减少,地震响应产生调谐效应。
[1]陈信平,刘素红.浅谈Gassmann方程[J].中国海上油气,1996,11(2):122~127.
[2]刘亚茹.储层流体特征及AVO地震响应分析[J].中国西部油气地质,2007,11:85~89.
[3]傅戈平.多属性AVO分析及叠前参数反演方法研究.成都理工大学毕业设计论文.
[4]林凯,贺振华,熊晓军,黄德济.基于Gassmann方程的流体替换流程[J].长江大学学报自然科学版,2009,6(1):180~181amp;205.
[5]林凯,钟结麟,贺振华,熊晓军.基于Gassmann方程岩石速度倒转现象成因分析.成都理工大学油气藏地质及开发工程国家重点实验室.
注:肖风凯、王茂均 为共同第一作者。

