合作博弈框架下出租车合乘费用分摊问题研究

刘华杰

(兰州交通大学,甘肃兰州 730000)

合作博弈框架下出租车合乘费用分摊问题研究

刘华杰

(兰州交通大学,甘肃兰州 730000)

本文运用合作博弈理论对出租车合乘费用分摊问题进行了研究,建立了合乘费用分摊的合作博弈模型,并运用Shapley值法对模型进行了求解,最后用算例证明了所建模型的有效性。

出租车合乘 费用分摊 合作博弈 Shapley值法

出租车合乘因其既克服了其他公共交通定时、定点的缺点、能实现“门到门”的服务，同时又节省了单个乘客的出行费用而日益成为一种新的出行方式。但是出租车合乘在我国的发展却非常缓慢，其原因是多方面的，其中主要原因是合乘的费用分摊问题没有解决。在合乘系统中乘客与乘客之间是一种既竞争又合作的关系，他(她)们通过合作或妥协来达到整体最优(即整体费用最小)，在对合作剩余进行分配时又处于一种竞争状态[1]，而目前现实中采用的费用分摊方案不能很好的反映这种复杂的关系，因此饱受诟病。本文在合作博弈的框架下对出租车合乘费用分摊问题进行了研究，建立了合乘费用分摊模型，并运用Shapley值法对模型进行了求解[2]-[4]，最后用算例证明了上述模型的可行性。

1 模型建立

定义:n个人合乘费用函数是定义在R(N)上的实函数c，对于表示联盟S合乘时局中人应承担的总成本。，其中C是联盟的固定成本，在该合乘系统中即合乘的起步价，c'(S)为联盟的可变成本；c(i)表示第i个人单独完成时所需承担的成本，c'(i)为第i个人单独完成时所需承担的可变成本；表联盟S中第i个局中人最终需支付的费用。假设:

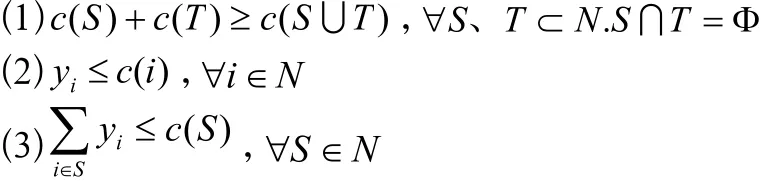
1.1 利用Shapley值法对联盟中可变费用进行分摊

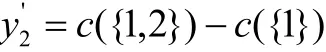
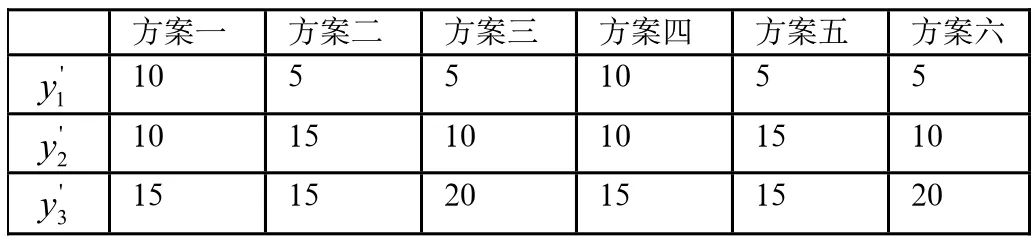
表1 分摊方案分析表

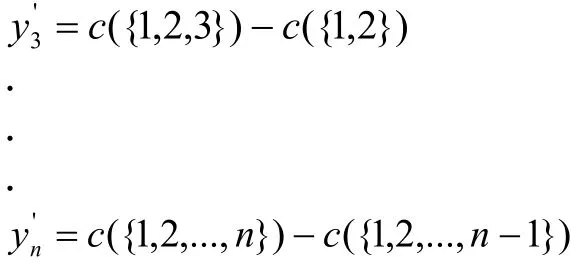
然而上述分摊与局中人的编号次序有关，不同的编号对应不同的分摊方案，对于有个局中人的联盟而言共有n!种分摊方案。设为第i个局中人在该n!种分摊方案中的平均值，则

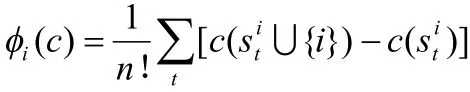
1.2 以Shapley值为基础计算固定成本分摊权重

设ti为局中人i在分摊固定成本时所占的权重

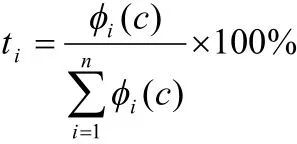
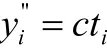
综上所述，第i个局中人在联盟S中最终需承担的费用

2 算例分析

分析如下:3个人的联盟共有3!=6种分摊方案，每种分摊方案的结果如表1。

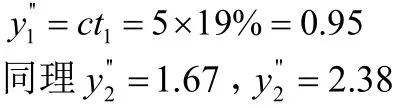
3 结语

根据出租车合乘的实际情况及合作博弈联盟形成的条件，用假设的方式给出n个人形成稳定联盟的条件:

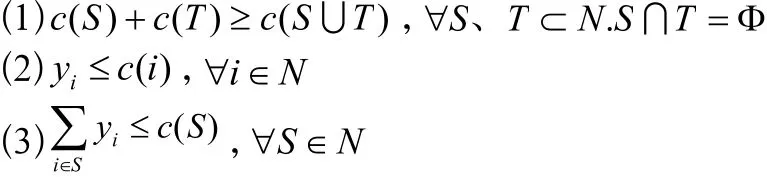
对联盟可变费用进行分摊时利用Shapley值法求出在有n个局中人的联盟中第i个局中人的费用分摊函数，进而求出联盟中所有局中人的费用分摊集合

结合局中人在可变费用分摊时的S h a p l e y值，利用求出每个局中人在固定费用中所占权重，进而对固定费用进行分摊。

综合局中人在可变费用、固定费用分摊的结果给出局中人在联盟S中总的费用分摊方案

通过算例验证了上述模型在费用分摊问题满足凸性条件时是有效的，即当费用分摊问题满足凸性条件时，将合作博弈的思想运用于出租车合乘费用分摊问题是可行的。

[1]郑士源.合作博弈理论的研究进展——联盟的形成机制及稳定性研究综述[J].上海海事大学学报,2011(4):53-59.

[2]孔祥荣,韩伯棠.基于合作博弈的运输分配方法[J].系统工程理论与实践,2010(7):1340-1344.

[3]蒋鹏飞.合作博弈解及其应用研究[D].山东:山东大学,2007:23-29.

[4]李军林,李岩.合作博弈理论及其发展[J].经济学动态,2004(9):79-84.

[5]陈伟,查迎春.关于成本分摊的合作博弈方法[J].运筹与管理,2004(2):54-57.

[6]赵耀华,蒲勇健.博弈论与经济模型[M].北京:中国人民大学出版社,2010:296-300.

[7]郑士源.基于核心解的运输联盟的费用分摊[J].系统工程,2013(8):47-53.

[8]谭春桥,张强.合作对策理论及应用[M].北京:科学出版社,2011.

In this paper, the taxi-pooling cost-sharing problem is studied and a taxipooling cost-sharing model is established based on the cooperative game theory. And the Shapley value method is used to solve the model. Finally, using an example proves the validity of the model.

taxi-pooling cost-sharing cooperative game shapley value method

刘华杰(1989—),女,河南周口人,硕士研究生,兰州交通大学研究生在读,研究方向:交通运输规划与管理、交通流信号控制及博弈论在交通运输规划中的应用研究。